第三種電気主任技術者試験(電験三種)
交流回路その1学習ページ
発電・送電・配電から家庭の電化製品まで、あらゆる場面で交流回路の知識が活用されています。
第1節 正弦波交流の特徴
1. 正弦波交流の発生
交流(Alternating Current, AC)は、時間とともに大きさと向きが周期的に変化する電流のことです。私たちが日常的に使用している家庭用電源(100V、50Hzまたは60Hz)も交流です。交流には様々な波形がありますが、最も基本的で重要なのが正弦波交流です。正弦波交流は、数学的に美しい性質を持ち、実用上も非常に重要な意味を持っています。
正弦波交流が自然界で重要な理由は、フーリエ解析の理論により明らかになります。任意の周期的な波形は、異なる周波数の正弦波の重ね合わせとして表現できます。これは、複雑な交流現象を理解する上で基礎となる重要な概念です。また、正弦波交流は三角関数(sin、cos)で表現され、微分・積分しても正弦波のままであるという数学的性質があり、回路解析を大幅に簡素化します。例えば、sinを微分するとcos、cosを微分すると-sinとなり、常に三角関数の形を保ちます。
三角関数の基礎理解
電験三種 数学基礎 | 三角関数インタラクティブ解説ツール正弦波交流の発生原理を理解するために、最も基本的な交流発電機の動作を考えてみましょう。コイルが一様な磁界中で一定の角速度で回転すると、ファラデーの電磁誘導の法則により、コイルには誘起電圧が発生します。この誘起電圧は、コイルと磁界のなす角度の正弦に比例するため、自然に正弦波となります。これが、発電所の巨大な発電機から小さなダイナモまで、すべての回転型発電機が正弦波を生成する物理的な理由です。
一様な磁束密度 \(B\) の磁界中で、面積 \(S\) のコイルが角速度 \(\omega\) で回転するとき、磁束 \(\Phi\) は時間 \(t\) の関数として次のように表されます。磁束鎖交数は \(\Phi = BS\cos(\omega t)\) となり、ファラデーの法則 \(e = -\frac{d\Phi}{dt}\) を適用すると、誘起電圧は正弦波となります。
ここで、\(E_m = BS\omega\):最大値(振幅)[V]
実際の発電機では、より効率的な発電のために多相交流が用いられます。三相交流発電機では、120度ずつ位相の異なる3つの巻線が配置され、平衡した三相電圧が発生します。これにより、単相交流に比べて電力の脈動が少なく、より効率的な電力伝送が可能になります。また、回転機の振動も軽減されるため、大容量発電機には必須の技術となっています。
正弦波交流の一般的な表現は、振幅(最大値)、角周波数、初期位相の3つのパラメータを用いて行われます。電圧の場合、瞬時値 \(v(t)\) は次のように表されます。この式は、交流回路解析の出発点となる最も基本的な式です。
\(V_m, I_m\):最大値、\(\omega\):角周波数、\(\phi, \psi\):初期位相
磁束密度 \(B = 0.5\) [T]、コイルの面積 \(S = 0.1\) [m²]、回転速度 \(n = 1800\) [rpm] の発電機の誘起電圧の最大値を求めよ。
解答:
角速度:
\[ \begin{aligned} \omega &= 2\pi n / 60 \\[10pt] &= 2\pi \times 1800 / 60 \\[10pt] &= 60\pi \quad \mathrm{[rad/s]} \end{aligned} \]誘起電圧の最大値:
\[ \begin{aligned} E_m &= BS\omega \\[10pt] &= 0.5 \times 0.1 \times 60\pi \\[10pt] &= 3\pi ≈ 9.42 \quad \mathrm{[V]} \end{aligned} \]共振現象も正弦波交流の重要な特性の一つです。LC回路やRLC回路では、特定の周波数で共振が起こり、回路のインピーダンスが最小(直列共振)または最大(並列共振)になります。この現象は、ラジオの同調回路、フィルタ回路、電力系統の共振現象など、様々な場面で重要な役割を果たします。
高調波の問題も現代の電力システムにおいて重要です。パワーエレクトロニクス機器の普及により、電力系統には基本波(50Hzまたは60Hz)以外の高調波成分が含まれるようになりました。これらの高調波は、電力品質の劣化、機器の過熱、通信障害などの問題を引き起こすため、適切な対策が必要です。
2. 平均値と実効値
交流の大きさを表現する方法として、最大値以外に平均値と実効値という重要な概念があります。直流では電圧や電流は一定値ですが、交流では時間とともに変化するため、その「代表値」をどのように定義するかが重要な問題となります。特に実効値は、交流の実用的な大きさを表す最も重要な量で、私たちが普段使っている「100V」という表示も実効値です。
平均値は、一周期間の平均的な大きさを表します。しかし、正弦波交流の場合、正の半周期と負の半周期で大きさが等しく符号が逆になるため、全周期にわたる平均値は零になってしまいます。そこで、実用的には半周期(0からπまで)の平均値を考えます。これを平均値または整流値と呼びます。
実効値(Root Mean Square, RMS)は、交流の「実効的な」大きさを表す量で、「同じ抵抗に同じ時間流したときに同じ電力を消費する直流の値」として定義されます。これは、交流回路における電力計算や発熱計算において極めて重要な概念です。実効値は、瞬時値の2乗の平均の平方根として数学的に定義されます。
同様に、\(I_{rms} = \frac{I_m}{\sqrt{2}}\)
この実効値の定義から、正弦波交流における電力の計算が可能になります。抵抗 \(R\) に実効値 \(I\) の交流電流を流したときの電力は、\(P = I^2 R\) となり、これは直流の場合と全く同じ式になります。これが実効値の「実効的」な意味です。
最大値が 141.4 [V] の正弦波交流電圧について、平均値と実効値を求めよ。
解答:
平均値:
\[ \begin{aligned} V_{av} &= 0.637 \times V_m \\[10pt] &= 0.637 \times 141.4 \\[10pt] &= 90.1 \quad \mathrm{[V]} \end{aligned} \]実効値:
\[ \begin{aligned} V_{rms} &= 0.707 \times V_m \\[10pt] &= 0.707 \times 141.4 \\[10pt] &= 100 \quad \mathrm{[V]} \end{aligned} \]この値は家庭用電源の実効値100Vに相当する。
波形率と波高率は、交流波形の形状を特徴づける重要な指標です。波形率(Form Factor)は実効値と平均値の比で、波高率(Crest Factor)は最大値と実効値の比です。正弦波ではこれらの値は一定ですが、他の波形では異なる値となり、波形の判別や歪みの評価に用いられます。
計測器の指示についても理解が必要です。可動コイル形(直流用)計器は平均値に比例した指示を示し、可動鉄片形計器は実効値に比例した指示を示します。そのため、正弦波以外の波形を測定する場合、計器の種類によって異なる読み値が得られることがあります。これは実用上重要な知識です。
| 項目 | 記号 | 最大値との関係 | 数値 |
|---|---|---|---|
| 最大値 | \(V_m\) | \(V_m\) | 1.000 |
| 実効値 | \(V_{rms}\) | \(V_m/\sqrt{2}\) | 0.707 |
| 平均値 | \(V_{av}\) | \(2V_m/\pi\) | 0.637 |
3. 角周波数
角周波数は、正弦波交流を数学的に扱う上で極めて重要な概念です。通常の周波数(Hz)が1秒間の振動回数を表すのに対し、角周波数(rad/s)は単位時間あたりの位相の変化率を表します。回転ベクトルによる交流の表現や、微分・積分を含む回路計算において、角周波数を用いることで式が大幅に簡素化されます。
周波数 \(f\) [Hz] と角周波数 \(\omega\) [rad/s] の関係は、1回転が \(2\pi\) ラジアンであることから導かれます。1秒間に \(f\) 回転する場合、1秒間の位相変化は \(2\pi f\) ラジアンとなります。この関係は、交流回路解析において基本的な変換として頻繁に用いられます。
\(T\):周期 [s]
日本の商用電源周波数は、東日本が50Hz、西日本が60Hzです。これは歴史的な経緯によるもので、明治時代にドイツから50Hz、アメリカから60Hzの発電機を導入したことに起因します。角周波数で表すと、50Hzは \(100\pi\) rad/s、60Hzは \(120\pi\) rad/s となります。
角周波数の物理的意味は、回転するベクトルの角速度と考えると理解しやすくなります。複素平面上で長さ \(V_m\) のベクトルが角速度 \(\omega\) で回転するとき、その実軸への射影が \(V_m\cos(\omega t + \phi)\) となり、これが正弦波交流を表現します。この幾何学的解釈は、位相関係の理解に特に有効です。
(1) 商用電源50Hzの角周波数を求めよ。
(2) 角周波数 \(377\) rad/s の周波数と周期を求めよ。
解答:
(1) 50Hzの角周波数:
\[ \begin{aligned} \omega &= 2\pi f \\[10pt] &= 2\pi \times 50 \\[10pt] &= 100\pi ≈ 314 \quad \mathrm{[rad/s]} \end{aligned} \](2) \(\omega = 377\) rad/s の場合:
\[ \begin{aligned} f &= \frac{\omega}{2\pi} = \frac{377}{2\pi} ≈ 60 \quad \mathrm{[Hz]} \\[10pt] T &= \frac{1}{f} = \frac{1}{60} ≈ 0.0167 \quad \mathrm{[s]} \end{aligned} \]リアクタンスの計算においても角周波数は重要な役割を果たします。インダクティブリアクタンス \(X_L = \omega L\) とキャパシティブリアクタンス \(X_C = 1/(\omega C)\) は、いずれも角周波数に依存します。これらの周波数特性が、フィルタ回路や共振回路の動作原理となっています。
4. 位相と位相差
位相(Phase)は、正弦波交流の時間的な位置を表す重要な概念です。同じ振幅と周波数を持つ2つの正弦波でも、位相が異なれば時間的にずれた波形となります。交流回路では、電圧と電流の間に位相差が生じることが一般的であり、この位相差が回路の性質や電力の計算において決定的な役割を果たします。
位相差の概念を理解するために、2つの正弦波 \(v_1(t) = V_m\sin(\omega t)\) と \(v_2(t) = V_m\sin(\omega t + \phi)\) を考えてみましょう。\(v_2\) は \(v_1\) よりも位相が \(\phi\) だけ進んでいます。\(\phi > 0\) のとき「\(v_2\) は \(v_1\) より \(\phi\) だけ位相が進む」といい、\(\phi < 0\) のとき「位相が遅れる」といいます。
位相差は、時間差と周波数から計算することもできます。時間差を \(\Delta t\)、周波数を \(f\) とすると、位相差 \(\phi\) は次のように表されます。これは、波形の観測において実用的な関係式です。
\(\Delta t\):時間差 [s]、\(\phi_{deg}\):位相差 [度]
交流回路における位相差の発生メカニズムを理解することは重要です。純抵抗回路では電圧と電流の位相は一致しますが、インダクタンス成分があると電流が電圧より90度遅れ、キャパシタンス成分があると電流が電圧より90度進みます。実際の回路では、これらの成分が組み合わされて様々な位相差が生じます。
- 抵抗 R:電圧と電流の位相は一致(位相差 0°)
- インダクタンス L:電流が電圧より 90° 遅れ
- キャパシタンス C:電流が電圧より 90° 進み
- 一般の回路:上記の組み合わせにより 0° ~ ±90° の位相差
周波数60Hzの正弦波において、ある点の電圧が最大値になってから2.78ms後に別の点の電圧が最大値になった。この位相差を度とラジアンで求めよ。
解答:
位相差(度):
\[ \begin{aligned} \phi_{deg} &= 360° \times f \times \Delta t \\[10pt] &= 360° \times 60 \times 2.78 \times 10^{-3} \\[10pt] &= 60° \end{aligned} \]位相差(ラジアン):
\[ \begin{aligned} \phi &= \frac{\pi}{180°} \times 60° \\[10pt] &= \frac{\pi}{3} \quad \mathrm{[rad]} \end{aligned} \]または直接計算:
\[ \begin{aligned} \phi &= 2\pi f \Delta t \\[10pt] &= 2\pi \times 60 \times 2.78 \times 10^{-3} \\[10pt] &= \frac{\pi}{3} \quad \mathrm{[rad]} \end{aligned} \]位相の加法性は、交流回路解析において重要な性質です。同一周波数の正弦波は、ベクトル的に合成することができます。振幅 \(A_1\)、位相 \(\phi_1\) の正弦波と振幅 \(A_2\)、位相 \(\phi_2\) の正弦波を合成すると、結果も同一周波数の正弦波となり、その振幅と位相は三角法により求めることができます。
位相差が0度の場合を「同相」、180度の場合を「逆相」といいます。同相の場合は振幅が加算され、逆相の場合は振幅が減算されます。この性質は、雑音除去や信号処理において重要な応用があります。また、三相交流では各相が120度ずつ位相がずれており、これが三相電力の特性を決定しています。
電力と位相差の関係も重要です。交流回路における瞬時電力は \(p(t) = v(t)i(t)\) で表され、電圧と電流の位相差によって平均電力が決まります。位相差が90度の場合、平均電力は零となり、これを無効電力といいます。位相差が0度の場合に最大の有効電力が得られます。
- 正弦波交流の発生:回転コイルによる電磁誘導、\(e = BS\omega\sin(\omega t)\)
- 実効値:\(V_{rms} = V_m/\sqrt{2}\)、実用的な交流の大きさ
- 平均値:\(V_{av} = 2V_m/\pi\)、整流回路での重要な値
- 角周波数:\(\omega = 2\pi f\) [rad/s]、数学的取り扱いで重要
- 位相差:同一周波数正弦波間の時間的ずれ、回路特性を決定
- 周波数と時間の関係:\(\phi = 2\pi f \Delta t\)
- 係数の暗記:実効値係数0.707、平均値係数0.637を確実に覚える
- 角周波数:50Hz→314 rad/s、60Hz→377 rad/sの換算
- 位相差計算:度とラジアンの変換、時間差との関係
- 波形の関係:最大値、実効値、平均値の大小関係
- 単位に注意:角度の単位(度、ラジアン)、周波数の単位
- 計算ミス防止:πの値(3.14)、√2の値(1.414)の近似
| 地域 | 周波数 [Hz] | 角周波数 [rad/s] | 周期 [ms] | 実効値 [V] |
|---|---|---|---|---|
| 東日本 | 50 | 314 | 20 | 100 |
| 西日本 | 60 | 377 | 16.7 | 100 |
第2節 交流回路の基礎的な扱い
1. 正弦波交流のベクトル表示
正弦波交流をベクトルで表示する方法は、交流回路解析の最も強力な手法の一つです。時間とともに変化する正弦波を、回転するベクトル(フェーザー)として表現することで、複雑な位相関係や計算を幾何学的に理解できるようになります。この手法により、交流回路の解析は直流回路と同様の代数的操作に帰着され、大幅に簡素化されます。
ベクトル表示の基本原理は、複素平面上での回転運動にあります。長さが最大値に等しく、角速度 \(\omega\) で反時計回りに回転するベクトルを考えます。このベクトルの実軸への射影が、時間とともに正弦波状に変化します。ベクトルの長さを実効値とし、\(t = 0\) での角度を初期位相とすることで、正弦波交流を完全に表現できます。
実効値 \(V\)、角周波数 \(\omega\)、初期位相 \(\phi\) の正弦波交流 \(v(t) = \sqrt{2}V\sin(\omega t + \phi)\) は、複素数を用いて次のように表現されます。この表現では、時間項 \(e^{j\omega t}\) を共通因子として扱い、振幅と位相の情報のみを \(\dot{V}\) に集約します。
\(\dot{V}\):電圧のフェーザー(複素実効値)
フェーザーの表記法には、指数形式 \(Ve^{j\phi}\) と極形式 \(V\angle\phi\) があります。また、直交形式 \(V\cos\phi + jV\sin\phi\) で表すこともあります。これらの表記法は相互に変換可能であり、計算の内容に応じて使い分けます。乗除算では極形式が、加減算では直交形式が便利です。
\(v(t) = 141.4\sin(\omega t + 60°)\) [V] のフェーザーを、極形式、指数形式、直交形式で表せ。
解答:
実効値:
\[V = \frac{141.4}{\sqrt{2}} = 100 \quad \mathrm{[V]}\]極形式:
\[\dot{V} = 100\angle60° \quad \mathrm{[V]}\]指数形式:
\[\dot{V} = 100e^{j60°} = 100e^{j\pi/3} \quad \mathrm{[V]}\]直交形式:
\[ \begin{aligned} \dot{V} &= 100(\cos60° + j\sin60°) \\[10pt] &= 100(0.5 + j0.866) \\[10pt] &= 50 + j86.6 \quad \mathrm{[V]} \end{aligned} \]フェーザー図は、複数の交流量の位相関係を視覚的に表現する重要な図表です。横軸を実軸、縦軸を虚軸とする複素平面上に、各フェーザーを矢印で描きます。ベクトルの長さは実効値、水平軸からの角度は位相を表します。基準となる量(通常は電圧)を実軸上に置き、他の量との位相差を明確に示します。
フェーザーの演算規則は、複素数の演算規則と同じです。加法・減法では直交成分ごとに計算し、乗法・除法では絶対値は乗除、偏角は加減で計算します。これにより、キルヒホッフの法則や回路素子の電圧・電流関係を、代数的な式として扱うことができます。
ベクトル図の作図ツール
電験三種 交流回路 | 抵抗・リアクタンス・コンデンサのベクトル図インタラクティブ作図ツール各成分の大きさや位相関係を視覚的に確認しながら、回路の理解を深めることができます。
2. 抵抗Rだけの回路
純抵抗回路は、交流回路の最も基本的な形態であり、他の回路素子の特性を理解するための基準となります。抵抗では、電圧と電流の関係がオームの法則に従い、かつ両者の位相が完全に一致するという重要な特性があります。この特性により、抵抗回路における電力はすべて有効電力となり、熱として消費されます。
抵抗 \(R\) [Ω] に交流電圧 \(v(t) = \sqrt{2}V\sin(\omega t)\) を加えたとき、流れる電流は瞬時瞬時でオームの法則が成り立ちます。そのため、電流の波形も正弦波となり、電圧と全く同位相になります。これは、抵抗がエネルギーを蓄積せず、瞬時瞬時で消費するためです。
電圧と電流の位相差:0°
フェーザー表示では、電圧フェーザー \(\dot{V}\) と電流フェーザー \(\dot{I}\) は同じ方向を向き、大きさの比が抵抗値に等しくなります。これは直流回路と全く同じ関係であり、交流回路においても抵抗はインピーダンスとして実数値 \(R\) を持ちます。
純抵抗回路における電力について詳しく見てみましょう。瞬時電力は \(p(t) = v(t)i(t)\) で表され、電圧と電流の積となります。両者が同位相であるため、瞬時電力は常に正値を取り、平均電力(有効電力)は実効値の積となります。
抵抗 \(R = 50\) [Ω] に、実効値 100 [V]、周波数 50 [Hz] の正弦波電圧を加えた。
(1) 電流の実効値と最大値
(2) 消費電力
(3) 電圧と電流のフェーザー表示
解答:
(1) 電流:
\[ \begin{aligned} I &= \frac{V}{R} = \frac{100}{50} = 2 \quad \mathrm{[A]} \\[10pt] I_m &= \sqrt{2} \times I = 2\sqrt{2} ≈ 2.83 \quad \mathrm{[A]} \end{aligned} \](2) 消費電力:
\[ \begin{aligned} P &= VI = 100 \times 2 = 200 \quad \mathrm{[W]} \\[10pt] &\text{または} \quad P = I^2R = 2^2 \times 50 = 200 \quad \mathrm{[W]} \end{aligned} \](3) フェーザー表示(電圧を基準):
\[ \begin{aligned} \dot{V} &= 100\angle0° \quad \mathrm{[V]} \\[10pt] \dot{I} &= 2\angle0° \quad \mathrm{[A]} \end{aligned} \]交流における電力の計算では、瞬時電力と平均電力の概念が重要です。純抵抗回路では、瞬時電力は \(p(t) = 2VI(1 - \cos(2\omega t))\) となり、直流成分 \(VI\) と周波数 \(2\omega\) の脈動成分からなります。平均電力は直流成分に等しく、\(P = VI\) となります。
3. インダクタンスLだけの回路
純インダクタンス回路は、抵抗回路とは大きく異なる特性を示します。インダクタンス(コイル)には、電流の変化を妨げようとする性質があり、これにより電流が電圧より位相的に遅れる現象が生じます。この位相遅れは正確に90度であり、これがインダクタンス回路の最も重要な特徴です。
インダクタンスの基本的な電圧・電流関係は、ファラデーの電磁誘導の法則から導かれます。インダクタンス \(L\) [H] において、電流 \(i(t)\) が流れるとき、誘起される電圧は電流の時間微分に比例します。正弦波電流に対してこの関係を適用すると、電圧は電流より90度位相が進むことが分かります。
\(V_L = \omega LI = X_LI\)
誘導リアクタンス \(X_L = \omega L\) は、インダクタンスが交流に対して示す「抵抗」的な性質を表します。ただし、純粋な抵抗と異なり、リアクタンスでは電力の消費は起こりません。電流が電圧より90度遅れるため、平均電力は零となり、エネルギーは磁界との間で授受されるだけです。
フェーザー表示では、インダクタンスのインピーダンスは純虚数となります。これは、電圧フェーザーが電流フェーザーより90度進んでいることを表しています。数学的には、微分演算子 \(d/dt\) が \(j\omega\) に対応することから理解できます。
インダクタンス \(L = 0.1\) [H] に、実効値 100 [V]、周波数 50 [Hz] の正弦波電圧を加えた。
(1) 誘導リアクタンス
(2) 電流の実効値
(3) 電圧と電流の位相関係
(4) 平均電力
解答:
(1) 誘導リアクタンス:
\[ \begin{aligned} X_L &= 2\pi fL \\[10pt] &= 2\pi \times 50 \times 0.1 \\[10pt] &= 10\pi ≈ 31.4 \quad \mathrm{[Ω]} \end{aligned} \](2) 電流の実効値:
\[ \begin{aligned} I &= \frac{V}{X_L} = \frac{100}{31.4} ≈ 3.18 \quad \mathrm{[A]} \end{aligned} \](3) 位相関係:
電流は電圧より90度遅れ
\[ \begin{aligned} \dot{V} &= 100\angle0° \quad \mathrm{[V]} \\[10pt] \dot{I} &= 3.18\angle-90° \quad \mathrm{[A]} \end{aligned} \](4) 平均電力:
\[P = VI\cos(90°) = 100 \times 3.18 \times 0 = 0 \quad \mathrm{[W]}\]インダクタンス回路における無効電力は重要な概念です。平均電力は零ですが、電圧と電流の実効値の積で定義される無効電力 \(Q = VI\) [var] が存在します。この無効電力は、磁界エネルギーの蓄積と放出に関連しており、電力系統の運用において重要な管理対象となります。
周波数特性もインダクタンスの重要な性質です。誘導リアクタンス \(X_L = 2\pi fL\) は周波数に比例するため、周波数が高くなるほど電流を流しにくくなります。この性質を利用して、高周波を除去するローパスフィルタや、特定周波数で共振する回路などが構成されます。
4. 静電容量Cだけの回路
純キャパシタンス回路は、インダクタンス回路とは正反対の特性を示します。キャパシタンス(コンデンサ)では、電流が電圧より位相的に90度進みます。これは、キャパシタンスにおける電流が、電圧の時間変化率(微分)に比例するためです。この特性により、キャパシタンスは直流をカットし、交流を通す性質を持ちます。
キャパシタンスの基本的な電流・電圧関係は、\(Q = CV\) および \(i = dQ/dt\) から導かれます。正弦波電圧に対してこの関係を適用すると、電流は電圧の微分に比例し、結果として電流が電圧より90度位相が進むことが分かります。
\(I_C = \omega CV = \frac{V}{X_C}\)
容量リアクタンス \(X_C = 1/(\omega C)\) は、キャパシタンスが交流に対して示す「抵抗」的な性質を表します。誘導リアクタンスとは逆に、周波数に反比例するため、周波数が高くなるほど電流を流しやすくなります。この性質により、キャパシタンスは高周波通過や直流阻止の用途に使用されます。
フェーザー表示では、キャパシタンスのインピーダンスは負の虚数となります。これは、電流フェーザーが電圧フェーザーより90度進んでいることを表しています。数学的には、積分演算子 \(\int dt\) が \(1/(j\omega)\) に対応することから理解できます。
キャパシタンス \(C = 100\) [μF] に、実効値 100 [V]、周波数 50 [Hz] の正弦波電圧を加えた。
(1) 容量リアクタンス
(2) 電流の実効値
(3) 電圧と電流の位相関係
(4) 無効電力
解答:
(1) 容量リアクタンス:
\[ \begin{aligned} X_C &= \frac{1}{2\pi fC} \\[10pt] &= \frac{1}{2\pi \times 50 \times 100 \times 10^{-6}} \\[10pt] &= \frac{1}{0.0314} ≈ 31.8 \quad \mathrm{[Ω]} \end{aligned} \](2) 電流の実効値:
\[ \begin{aligned} I &= \frac{V}{X_C} = \frac{100}{31.8} ≈ 3.14 \quad \mathrm{[A]} \end{aligned} \](3) 位相関係:
電流は電圧より90度進み
\[ \begin{aligned} \dot{V} &= 100\angle0° \quad \mathrm{[V]} \\[10pt] \dot{I} &= 3.14\angle90° \quad \mathrm{[A]} \end{aligned} \](4) 無効電力:
\[Q_C = VI = 100 \times 3.14 ≈ 314 \quad \mathrm{[var]}\](進み無効電力)
キャパシタンス回路における電力の特性も重要です。電流が電圧より90度進むため、瞬時電力は正負を繰り返し、平均電力は零となります。しかし、キャパシタンスでも無効電力 \(Q_C = VI\) [var] が存在し、これは電界エネルギーの蓄積と放出に関連しています。キャパシタンスの無効電力は「進み無効電力」と呼ばれ、インダクタンスの「遅れ無効電力」とは逆の性質を持ちます。
キャパシタンスの周波数特性は、インダクタンスとは正反対です。容量リアクタンス \(X_C = 1/(2\pi fC)\) は周波数に反比例するため、周波数が高くなるほど小さくなり、より多くの電流を流します。直流(f = 0)では理論上無限大のリアクタンスとなり、電流は流れません。この性質により、キャパシタンスは直流阻止や高周波通過フィルタとして機能します。
実際の回路では、キャパシタンスとインダクタンスが組み合わされることが多く、両者のリアクタンスが等しくなる周波数で共振現象が起こります。共振周波数 \(f_0 = 1/(2\pi\sqrt{LC})\) において、誘導リアクタンスと容量リアクタンスが相殺され、回路は純抵抗的に動作します。
- 抵抗 R:電圧・電流同位相、有効電力消費、周波数無依存
- インダクタンス L:電流90°遅れ、遅れ無効電力、\(X_L ∝ f\)
- キャパシタンス C:電流90°進み、進み無効電力、\(X_C ∝ 1/f\)
これらの基本的な回路素子の理解は、複雑な交流回路の解析における基礎となります。実際の回路では、これらの素子が組み合わされてRLC回路を構成し、様々な周波数特性や位相特性を示します。また、電力系統においては、負荷の力率改善にキャパシタンスが使用され、インダクタンスによる遅れ無効電力を補償する重要な役割を果たしています。
| 素子 | インピーダンス | 大きさ | 位相角 | 電流の位相 |
|---|---|---|---|---|
| 抵抗 R | \(R\) | \(R\) | 0° | 電圧と同位相 |
| インダクタンス L | \(j\omega L\) | \(\omega L\) | +90° | 電圧より90°遅れ |
| キャパシタンス C | \(-j\frac{1}{\omega C}\) | \(\frac{1}{\omega C}\) | -90° | 電圧より90°進み |
- フェーザー表示:正弦波交流を複素数で表現、計算の簡素化
- 純抵抗回路:電圧・電流同位相、\(V = IR\)、有効電力のみ
- 純インダクタンス回路:電流90°遅れ、\(X_L = 2\pi fL\)、遅れ無効電力
- 純キャパシタンス回路:電流90°進み、\(X_C = 1/(2\pi fC)\)、進み無効電力
- リアクタンス:LとCの交流抵抗、周波数依存性が重要
- 無効電力:エネルギー蓄積・放出に関連、平均電力は零
- 位相関係の暗記:R(同位相)、L(電流遅れ)、C(電流進み)
- リアクタンス計算:\(X_L = 2\pi fL\)、\(X_C = 1/(2\pi fC)\)の公式
- フェーザー表示:極形式と直交形式の変換
- 電力計算:純リアクタンス回路では平均電力は零
- 周波数特性:Lは高周波で大、Cは高周波で小
- 単位換算:角度(度、ラジアン)、容量(μF、nF、pF)
[図2-1] RLC各素子のフェーザー図
電圧を基準(水平右向き)とした場合の電流フェーザーの向き:
- 抵抗:電流も水平右向き(同位相)
- インダクタンス:電流は垂直下向き(90°遅れ)
- キャパシタンス:電流は垂直上向き(90°進み)
| 周波数 | 抵抗 R | 誘導リアクタンス \(X_L\) | 容量リアクタンス \(X_C\) |
|---|---|---|---|
| 低周波 | 一定 | 小 | 大 |
| 高周波 | 一定 | 大 | 小 |
| 直流 (f=0) | R | 0(短絡) | ∞(開放) |
\(R = 50\) [Ω]、\(L = 0.1\) [H]、\(C = 100\) [μF] の各素子に、実効値100 [V]、周波数50 [Hz]の交流電圧を加えた場合を比較せよ。
解答:
抵抗の場合:
\[ \begin{aligned} I_R &= \frac{V}{R} = \frac{100}{50} = 2 \quad \mathrm{[A]} \\[10pt] P_R &= VI_R = 100 \times 2 = 200 \quad \mathrm{[W]} \\[10pt] \text{位相差} &= 0° \end{aligned} \]インダクタンスの場合:
\[ \begin{aligned} X_L &= 2\pi \times 50 \times 0.1 = 31.4 \quad \mathrm{[Ω]} \\[10pt] I_L &= \frac{V}{X_L} = \frac{100}{31.4} = 3.18 \quad \mathrm{[A]} \\[10pt] Q_L &= VI_L = 100 \times 3.18 = 318 \quad \mathrm{[var]} \\[10pt] \text{位相差} &= -90° \text{(電流遅れ)} \end{aligned} \]キャパシタンスの場合:
\[ \begin{aligned} X_C &= \frac{1}{2\pi \times 50 \times 100 \times 10^{-6}} = 31.8 \quad \mathrm{[Ω]} \\[10pt] I_C &= \frac{V}{X_C} = \frac{100}{31.8} = 3.14 \quad \mathrm{[A]} \\[10pt] Q_C &= VI_C = 100 \times 3.14 = 314 \quad \mathrm{[var]} \\[10pt] \text{位相差} &= +90° \text{(電流進み)} \end{aligned} \]これらの基本的な回路素子の特性を理解することで、より複雑なRLC回路や三相交流回路、電力系統の解析に進むことができます。特に、各素子の位相特性と周波数特性は、フィルタ回路、共振回路、電力系統の力率改善など、実用的な応用において極めて重要な知識となります。
5. R-L直列回路
R-L直列回路は、抵抗とインダクタンスが直列に接続された回路で、実際の電気機器において最も頻繁に見られる回路構成の一つです。モータのコイル、変圧器の巻線、送電線など、多くの電気設備がこの特性を持っています。この回路では、純抵抗の特性(電圧・電流同位相)と純インダクタンスの特性(電流90度遅れ)が組み合わされ、電流が電圧より0度から90度の間で遅れる特性を示します。
R-L直列回路における電圧と電流の関係を理解するために、キルヒホッフの電圧則をフェーザーで表現してみましょう。回路に流れる電流は共通ですが、抵抗とインダクタンスにかかる電圧はそれぞれ異なる位相を持ちます。抵抗電圧は電流と同位相、インダクタンス電圧は電流より90度進みます。
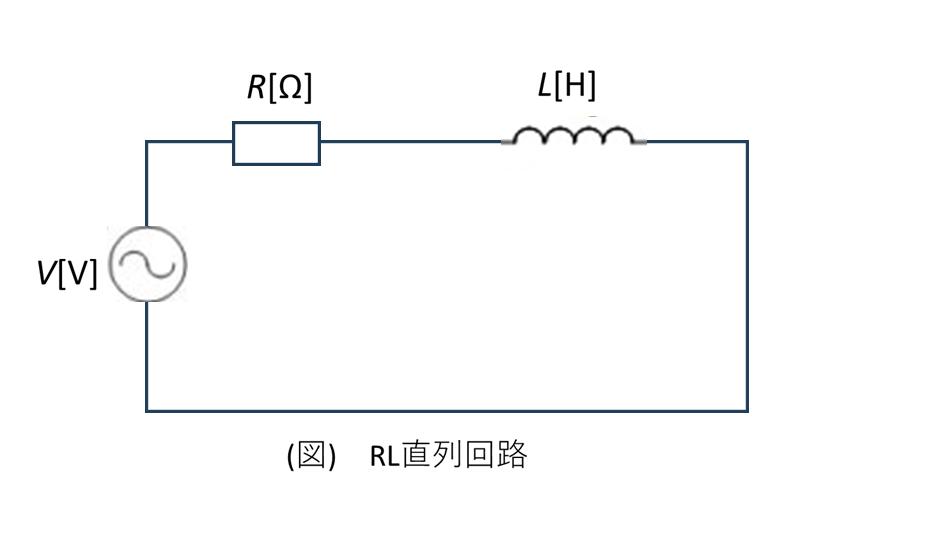
インピーダンスの概念は、R-L回路において特に重要です。抵抗成分(実数部)とリアクタンス成分(虚数部)を組み合わせたインピーダンス \(\dot{Z}\) により、オームの法則を交流回路でも適用できます。インピーダンスの大きさは電圧と電流の実効値の比を表し、位相角は電圧と電流の位相差を表します。
\(R = 30\) [Ω]、\(L = 0.1\) [H] の直列回路に、実効値100 [V]、周波数50 [Hz]の交流電圧を加えた。
(1) 誘導リアクタンス
(2) インピーダンスの大きさと位相角
(3) 電流の実効値
(4) 各部の電圧
解答:
(1) 誘導リアクタンス:
\[X_L = 2\pi fL = 2\pi \times 50 \times 0.1 = 31.4 \quad \mathrm{[Ω]}\](2) インピーダンス:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{R^2 + X_L^2} = \sqrt{30^2 + 31.4^2} \\[10pt] &= \sqrt{900 + 986} = \sqrt{1886} ≈ 43.4 \quad \mathrm{[Ω]} \\[10pt] \phi &= \arctan\left(\frac{X_L}{R}\right) = \arctan\left(\frac{31.4}{30}\right) \\[10pt] &= \arctan(1.047) ≈ 46.3° \end{aligned} \](3) 電流の実効値:
\[I = \frac{V}{|\dot{Z}|} = \frac{100}{43.4} ≈ 2.30 \quad \mathrm{[A]}\](4) 各部の電圧:
\[ \begin{aligned} V_R &= IR = 2.30 \times 30 = 69.0 \quad \mathrm{[V]} \\[10pt] V_L &= IX_L = 2.30 \times 31.4 = 72.2 \quad \mathrm{[V]} \\[10pt] \text{検算:} \quad V &= \sqrt{V_R^2 + V_L^2} = \sqrt{69.0^2 + 72.2^2} ≈ 100 \quad \mathrm{[V]} \end{aligned} \]フェーザー図を描くことで、R-L回路の電圧・電流関係を視覚的に理解できます。電流を基準とすると、抵抗電圧は電流と同方向、インダクタンス電圧は電流より90度進んだ方向になります。電源電圧は、これらのベクトル和として表されます。この図から、各電圧の大きさと位相関係が明確に分かります。
- 電流の位相:電圧より \(\phi = \arctan(X_L/R)\) だけ遅れ
- 電圧の関係:\(V^2 = V_R^2 + V_L^2\) (ピタゴラスの定理)
- 周波数特性:周波数が高いほど位相遅れが大きくなる
- 実用例:モータ、変圧器、送電線などの等価回路
6. R-C直列回路
R-C直列回路は、抵抗とキャパシタンスが直列に接続された回路で、電子回路や信号処理回路で広く使用されています。フィルタ回路、結合回路、微分回路など、様々な用途があります。この回路では、純抵抗の特性と純キャパシタンスの特性が組み合わされ、電流が電圧より0度から90度の間で進む特性を示します。これはR-L回路とは逆の位相関係です。
R-C直列回路のインピーダンスは、抵抗成分(実数部)と容量リアクタンス成分(負の虚数部)からなります。容量リアクタンスが負の値を持つため、全体のインピーダンスの位相角は負(進み)となります。この特性により、R-C回路は力率改善回路としても使用されます。
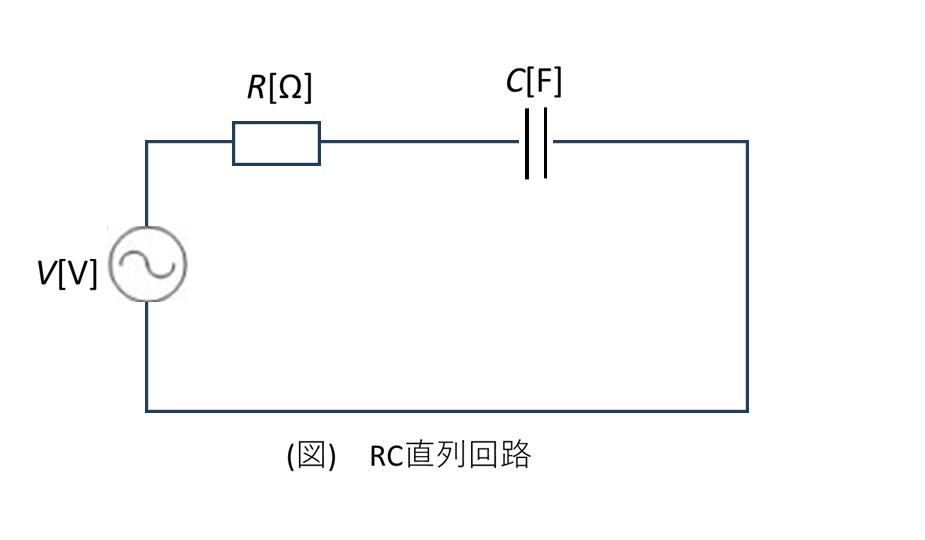
\(R = 40\) [Ω]、\(C = 100\) [μF] の直列回路に、実効値100 [V]、周波数50 [Hz]の交流電圧を加えた。
(1) 容量リアクタンス
(2) インピーダンスの大きさと位相角
(3) 電流の実効値と位相
解答:
(1) 容量リアクタンス:
\[X_C = \frac{1}{2\pi fC} = \frac{1}{2\pi \times 50 \times 100 \times 10^{-6}} ≈ 31.8 \quad \mathrm{[Ω]}\](2) インピーダンス:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{R^2 + X_C^2} = \sqrt{40^2 + 31.8^2} \\[10pt] &≈ 51.1 \quad \mathrm{[Ω]} \\[10pt] \phi &= -\arctan\left(\frac{X_C}{R}\right) = -\arctan\left(\frac{31.8}{40}\right) \\[10pt] &≈ -38.5° \end{aligned} \](3) 電流:
\[ \begin{aligned} I &= \frac{V}{|\dot{Z}|} = \frac{100}{51.1} ≈ 1.96 \quad \mathrm{[A]} \\[10pt] \text{電流は電圧より} &\text{ 38.5° 進む} \end{aligned} \]R-C回路の周波数特性は、フィルタ回路として重要な応用があります。低周波では容量リアクタンスが大きく、高周波では小さくなるため、R-C回路は高周波通過フィルタ(ハイパスフィルタ)として機能します。カットオフ周波数 \(f_c = 1/(2\pi RC)\) 以上で信号が通過しやすくなります。
7. R-L-C直列回路
R-L-C直列回路は、抵抗、インダクタンス、キャパシタンスが直列に接続された回路で、交流回路理論の集大成ともいえる重要な回路です。この回路では、誘導リアクタンスと容量リアクタンスが互いに打ち消し合う作用があり、特定の周波数で共振現象が起こります。実際の電力系統や通信回路において、この共振現象は重要な役割を果たします。
R-L-C回路のインピーダンスは、3つの成分の複素数的な合成により求められます。誘導リアクタンスは正の虚数、容量リアクタンスは負の虚数として表されるため、両者の差が回路全体のリアクタンス成分となります。この結果、周波数によって回路特性が大きく変化します。
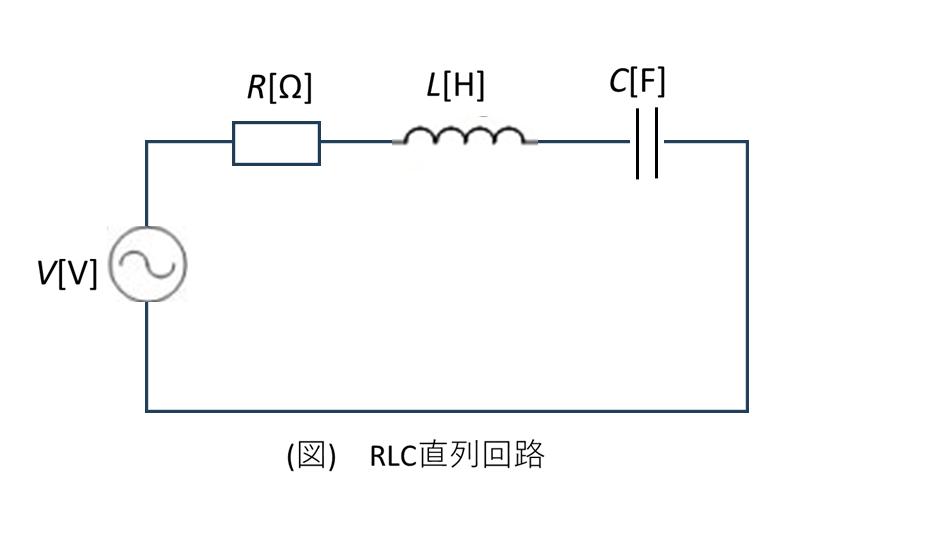
R-L-C回路の特性は周波数によって大きく変化します。低周波では容量リアクタンスが支配的となり回路は容量性、高周波では誘導リアクタンスが支配的となり回路は誘導性を示します。そして、\(X_L = X_C\) となる特定の周波数で共振が起こり、回路は純抵抗的に動作します。
\(R = 10\) [Ω]、\(L = 0.01\) [H]、\(C = 100\) [μF] の直列回路について、周波数50 [Hz]での特性を求めよ。
解答:
各リアクタンス:
\[ \begin{aligned} X_L &= 2\pi \times 50 \times 0.01 = 3.14 \quad \mathrm{[Ω]} \\[10pt] X_C &= \frac{1}{2\pi \times 50 \times 100 \times 10^{-6}} = 31.8 \quad \mathrm{[Ω]} \end{aligned} \]インピーダンス:
\[ \begin{aligned} X_L - X_C &= 3.14 - 31.8 = -28.66 \quad \mathrm{[Ω]} \\[10pt] |\dot{Z}| &= \sqrt{10^2 + (-28.66)^2} = \sqrt{100 + 821} ≈ 30.3 \quad \mathrm{[Ω]} \\[10pt] \phi &= \arctan\left(\frac{-28.66}{10}\right) ≈ -70.8° \end{aligned} \]この周波数では容量性(電流進み)の回路となる。
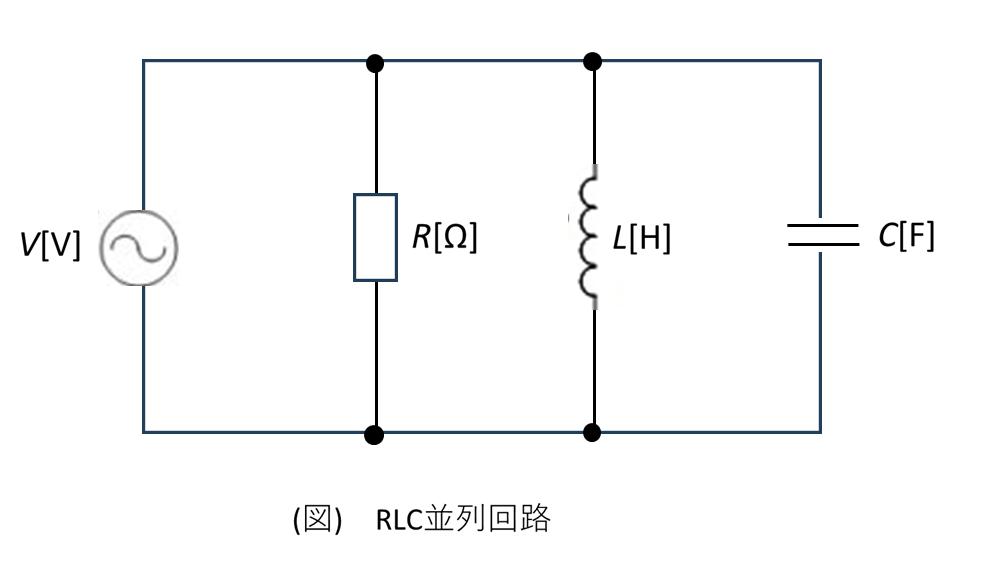
8. R-L-C並列回路
R-L-C並列回路は、各素子が並列に接続された回路で、電力系統の負荷や電子回路のフィルタなどで重要な役割を果たします。直列回路とは異なり、各素子に同じ電圧が加わり、電流が分岐します。この回路の解析には、インピーダンスではなくアドミタンス(インピーダンスの逆数)を用いると便利です。
並列回路のアドミタンスは、各素子のアドミタンスの和として表されます。抵抗のアドミタンスをコンダクタンス \(G = 1/R\)、インダクタンスのアドミタンスをサセプタンス \(B_L = -1/X_L\)、キャパシタンスのアドミタンスをサセプタンス \(B_C = 1/X_C\) と呼びます。
ベクトル図の作図ツール
電験三種 交流回路 | 抵抗・リアクタンス・コンデンサのベクトル図インタラクティブ作図ツール各成分の大きさや位相関係を視覚的に確認しながら、回路の理解を深めることができます。
9. 直列共振回路
直列共振は、R-L-C直列回路において誘導リアクタンスと容量リアクタンスが等しくなる現象です。共振周波数では、リアクタンス成分が相殺され、回路は純抵抗的に動作します。この時、インピーダンスは最小となり、電流は最大となります。直列共振は、ラジオの同調回路、フィルタ回路、電力系統の共振現象など、様々な分野で重要な役割を果たします。
共振周波数 \(f_0\) は、\(X_L = X_C\) の条件から導出されます。この周波数は回路の L と C の値のみで決まり、抵抗値には依存しません。共振時の特性を理解することは、回路設計や故障解析において極めて重要です。
共振の鋭さを表す量として、Q値(品質係数)があります。Q値が高いほど共振が鋭く、周波数選択性が良好になります。一方、Q値が低いと共振が緩やかで、広帯域特性を示します。この特性は、フィルタ回路の設計において重要なパラメータとなります。
共振周波数1 [kHz]、Q値50の直列共振回路を設計する。\(L = 10\) [mH]とした時、必要な C と R を求めよ。
解答:
必要なキャパシタンス:
\[ \begin{aligned} f_0 &= \frac{1}{2\pi\sqrt{LC}} = 1000 \\[10pt] C &= \frac{1}{(2\pi f_0)^2 L} = \frac{1}{(2\pi \times 1000)^2 \times 10 \times 10^{-3}} \\[10pt] &= 2.53 \times 10^{-6} \quad \mathrm{[F]} = 2.53 \quad \mathrm{[μF]} \end{aligned} \]必要な抵抗値:
\[ \begin{aligned} Q &= \frac{X_L}{R} = 50 \\[10pt] X_L &= 2\pi f_0 L = 2\pi \times 1000 \times 10 \times 10^{-3} = 62.8 \quad \mathrm{[Ω]} \\[10pt] R &= \frac{X_L}{Q} = \frac{62.8}{50} = 1.26 \quad \mathrm{[Ω]} \end{aligned} \]10. 並列共振回路
並列共振は、L-C並列回路において生じる共振現象で、直列共振とは特性が大きく異なります。並列共振では、共振周波数でインピーダンスが最大となり、回路に流れる電流が最小となります。また、L と C の間では大きな循環電流が流れますが、電源からの電流は最小となるため、「電流共振」や「反共振」とも呼ばれます。
理想的な L-C並列回路(抵抗成分がない場合)では、共振周波数で回路のインピーダンスは無限大となり、電源電流は零となります。しかし、実際の回路では抵抗成分があるため、インピーダンスは有限の最大値を持ちます。この現象は、電力系統の力率改善や発振回路などで利用されます。
並列共振回路は、選択性の高いフィルタとして重要な応用があります。共振周波数では高いインピーダンスを示すため、その周波数成分をカットする帯域阻止フィルタ(ノッチフィルタ)として機能します。また、発振回路では正帰還ループ内に並列共振回路を配置することで、特定周波数での発振を実現します。
- 共振周波数:どちらも \(f_0 = 1/(2\pi\sqrt{LC})\)
- 直列共振:インピーダンス最小、電流最大、電圧共振
- 並列共振:インピーダンス最大、電流最小、電流共振
- 応用:直列は同調回路、並列は阻止フィルタ
続きは、下記のリンクからご覧いただけます。 交流回路その2|電験三種 完全攻略テキスト|第三種電気主任技術者の基礎から応用まで体系的学習