🎯 まずは動きを見てみよう!誘導電動機の回転原理
💫 誘導電動機の動作を直感的に理解
三相交流が作る磁界の動き
負荷による速度変化を実感
同期速度・実速度の関係
この後の理論説明がスムーズに頭に入ります!(所要時間:約3分)
第三種電気主任技術者試験(電験三種)
誘導機学習ページ
特に三相誘導電動機は、構造が堅牢で保守が容易なため、産業界で最も広く使用されている電動機です。
回転磁界によって回転子に誘導電流を流し、その電流と磁界の相互作用により回転トルクを発生させます。
第1節 三相誘導電動機の仕組みと構造
1. 三相誘導モーターの動作原理
三相誘導電動機は、1888年にニコラ・テスラが開発した画期的な電動機械です。その作動メカニズムは、固定子部分に形成される回転する磁場と、回転子部分に生じる誘導電流との間の相互作用によって回転力を創出することにあります。この基本原理は、ファラデーの電磁誘導法則に基づいており、変圧器の動作原理と本質的に類似しています。この電動機が「誘導」機と称される理由は、回転子に直接的な電流供給を行わず、固定子の磁場変化によって間接的に電流を誘起させるためです。
回転磁場の生成メカニズム
三相誘導電動機の動作理解において最初に把握すべきは、回転磁場の発生原理です。固定子には120度の電気角差を持つ三相巻線が設置され、これに三相交流電流を通電することで時間的に変動する磁場が構築されます。各相の電流は正弦波状に変化し、それらの合成磁場は一定の磁束密度を維持しながら空間的に回転する「回転磁場」を形成します。
この回転磁場の回転速度は「同期回転数」と呼ばれ、電源周波数と磁極数によって決定されます。日本の商用電源周波数50Hzの場合、2極機では3000min⁻¹、4極機では1500min⁻¹で回転磁場が回転します。この同期回転数の計算式は、誘導機の基礎理論として必須の知識です。
ここで、\(N_s\):同期回転数 [min⁻¹]、\(f\):電源周波数 [Hz]、\(p\):磁極数
周波数60Hz、4極の三相誘導電動機の同期回転数を算出せよ。
解答:
\[ \begin{aligned} N_s &= \frac{120f}{p} \\[10pt] &= \frac{120 \times 60}{4} \\[10pt] &= \frac{7200}{4} \\[10pt] &= 1800 \, \mathrm{[min^{-1}]} \end{aligned} \]すべりとトルク発生
回転子が回転磁場と完全に同期して回転すると、両者の相対速度が零になり、回転子導体には誘導電流が流れません。実際の動作では、回転子は同期回転数より僅かに低い回転数で動作します。この回転数の差を「すべり」と呼び、このすべりの存在により回転子に誘導電流が発生し、回転力が生まれます。すべりは誘導機の動作において極めて重要な要素で、負荷の変化に応じて変動します。
ここで、\(s\):すべり、\(N_s\):同期回転数 [min⁻¹]、\(N\):回転子回転数 [min⁻¹]
すべりの物理的意味を具体例で説明すると、同期回転数1500min⁻¹の誘導電動機が1450min⁻¹で回転している場合、すべりは\(s = \frac{1500-1450}{1500} = 0.033\)(3.3%)となります。軽負荷運転時のすべりは1~3%程度、定格負荷運転時でも5%程度と比較的小さな値ですが、この微小なすべりがトルク発生に必要不可欠です。
誘導電流の発生原理
回転子導体は回転磁場に対して相対運動を行うため、レンツの法則により起電力が誘導されます。回転子が籠型構造の場合、この誘導起電力によって回転子導体に電流が流れます。この電流の方向は、回転磁場の変化を阻止する方向、つまり回転磁場の回転を促進する方向となります。これが誘導電動機の「自己調整機能」の基本原理です。
回転子に流れる電流の周波数は、すべり周波数と称され、電源周波数にすべりを乗じた値になります。例えば、50Hzの電源ですべりが0.05の場合、回転子電流の周波数は2.5Hzとなります。これは回転子から見た磁場の変化速度を表し、すべりが小さいほど回転子電流の周波数も低くなります。
ここで、\(f_r\):回転子電流の周波数 [Hz]、\(s\):すべり、\(f\):電源周波数 [Hz]
回転力の発生と継続
回転子に流れる誘導電流は、固定子の回転磁場と相互作用して回転力を発生します。フレミングの左手の法則により、電流と磁場の相互作用で力が発生し、この力が回転軸回りの回転力となります。発生する回転力の大きさは、磁束密度、電流の大きさ、および両者の位相関係によって決まります。
重要な点は、誘導電動機の回転力がすべりに依存することです。すべりが零では電流が流れず回転力も零となり、すべりが過大になると効率が低下します。適切なすべり範囲で運転することで、効率的な回転力発生が実現されます。これが誘導電動機の「自己調整機能」であり、負荷が増加すると自動的にすべりが増加して回転力が増大し、負荷の要求に対応します。
同期回転数1800min⁻¹の三相誘導電動機が1740min⁻¹で回転している。すべりとすべり周波数(電源周波数60Hz)を求めよ。
解答:
すべり:
\[s = \frac{N_s - N}{N_s} = \frac{1800 - 1740}{1800} = \frac{60}{1800} = 0.033\]すべり周波数:
\[f_r = s \cdot f = 0.033 \times 60 = 2.0 \, \mathrm{[Hz]}\]2. 主な種類と構造の特徴
三相誘導電動機は、回転子の構造形式によって主に「かご型誘導電動機」と「巻線型誘導電動機」に分類されます。両者は基本的な動作原理は同一ですが、構造的特性と適用分野が大きく相違します。かご型は構造が簡素で保守が容易である反面、始動特性や速度調整に制約があります。一方、巻線型は構造が複雑ですが、始動特性の向上や速度調整が容易という利点があります。
固定子(ステータ)の構造
固定子は誘導電動機の静止部分で、三相の交流巻線を収納する重要な構成要素です。固定子鉄心は薄い珪素鋼板を積層した構造で、これによって鉄損(うず電流損失とヒステリシス損失)を最小限に抑制しています。鉄心には多数のスロット(溝)が設けられ、そこに三相巻線が規則正しく配置されています。
三相巻線は、互いに120度の電気角をなすように配置され、これによって回転磁場が形成されます。巻線の配置方法には「集中巻き」と「分布巻き」があり、分布巻きは磁束分布を正弦波に近づけ、高調波を減少させる効果があります。また、「全節巻き」と「短節巻き」の選択により、巻線係数や高調波含有率を調整できます。
かご型回転子の構造と特徴
かご型誘導電動機の回転子は、「鳥かご」のような形状からその名前が付けられました。回転子鉄心の外周にスロットが設けられ、そこにアルミニウムや銅の導体棒が埋め込まれています。導体棒の両端は、エンドリングによって短絡され、全体として一つの閉回路を形成しています。この構造により、回転子巻線のような複雑な接続を必要としない簡潔な設計が実現されています。
かご型回転子の最大の長所は、その構造の簡素さと頑丈さです。回転部分に摺動接点がないため、保守がほとんど不要で、長期間にわたって安定した運転が可能です。また、製造コストも低く抑えることができます。一方で、始動時の電流が大きく、始動トルクの調整が困難という短所もあります。
巻線型回転子の構造と特徴
巻線型誘導電動機の回転子には、固定子と同様に三相巻線が配置されています。回転子巻線の各相は、回転軸に設けられたスリップリングに接続され、カーボンブラシを通じて外部回路と電気的に接続されます。この構造により、回転子回路に外部抵抗を挿入したり、回転子電流を制御したりすることが可能になります。
巻線型の主な長所は、始動特性の向上が可能なことです。始動時に回転子回路に抵抗を挿入することで、始動電流を抑制しながら大きな始動トルクを得ることができます。また、回転子回路の抵抗を変えることで、ある程度の速度制御も可能です。しかし、スリップリングとブラシという摺動接点があるため、定期的な保守が必要であり、製造コストも高くなります。
| 項目 | かご型誘導電動機 | 巻線型誘導電動機 |
|---|---|---|
| 構造 | 簡素・頑丈 | 複雑 |
| 保守 | ほとんど不要 | 定期保守必要 |
| 始動電流 | 大(5~7倍) | 小(2~3倍) |
| 始動トルク | 小~中 | 大 |
| 速度制御 | 困難 | 可能 |
| コスト | 低 | 高 |
| 用途 | 一般工業用 | 特殊用途 |
冷却方式と保護構造
誘導電動機の冷却方式は、運転時に発生する損失を効率的に除去するために重要です。最も一般的な「自己冷却式」では、回転子に取り付けられたファンによって空気を循環させます。大容量機では「強制冷却式」が採用され、外部ファンによって冷却空気を強制的に送り込みます。さらに大容量の機器では、水冷や油冷などの液体冷却方式も使用されます。
保護構造は、使用環境に応じて選択される重要な仕様です。IP(Ingress Protection)等級により、固形物の侵入と水の浸入に対する保護度が規定されています。例えば、IP44は直径1mm以上の固形物と飛沫に対して保護されていることを意味します。屋外や湿潤環境では、より高い保護等級の電動機が必要になります。
効率規格と省エネ技術
近年、エネルギー効率の改善が重要な課題となっており、誘導電動機においても高効率化が進んでいます。JIS C 4212では効率クラスが規定され、プレミアム効率モータ(IE3)やスーパープレミアム効率モータ(IE4)などの高効率機種が普及しています。これらの高効率化は、材料の改良、設計の最適化、製造精度の向上などにより実現されています。
- 銅損:固定子・回転子巻線の抵抗による損失
- 鉄損:鉄心のヒステリシス損失とうず電流損失
- 機械損:軸受摩擦損、風損など
- 漂遊負荷損:高調波による追加損失
入力電力10kW、機械出力9.2kWの三相誘導電動機の効率を求めよ。
解答:
\[ \begin{aligned} \eta &= \frac{P_{out}}{P_{in}} \times 100 \\[10pt] &= \frac{9.2}{10.0} \times 100 \\[10pt] &= 92.0 \, \mathrm{[\%]} \end{aligned} \]- 同期回転数:\(N_s = \frac{120f}{p}\) [min⁻¹]
- すべり:\(s = \frac{N_s - N}{N_s}\)
- 回転磁場:三相電流により発生する一定強度の回転磁場
- かご型:構造簡素、保守容易、一般用途
- 巻線型:始動特性良好、速度制御可能、特殊用途
- 自己調整機能:負荷増加→すべり増加→トルク増加
- 同期回転数計算:周波数と極数から正確に計算
- すべりの概念:定義式と物理的意味を理解
- 構造の違い:かご型と巻線型の特徴を比較
- 回転磁場:三相電流による回転磁場の発生原理
- すべり周波数:\(f_r = s \cdot f\)の関係式
- 応用問題:実際の数値を使った計算練習
第2節 三相誘導電動機の理論と回路
1. 起磁力・誘導起電力の概要
固定子巻線への三相交流供給により生成される回転磁界は、誘導電動機の動作原理の根幹を成します。この磁界が回転子導体と交差する際、電磁誘導の法則に従って回転子内に起電力が誘起されます。誘起された起電力により回転子導体に電流が発生し、この電流による磁界と固定子磁界の相互作用がトルクを生み出します。固定子側では、回転子電流による磁界変化を補償するための電流が追加的に流れ、結果としてエアギャップ磁束密度が一定に維持されます。このメカニズムは変圧器における磁束結合と類似しており、固定子を一次側、回転子を二次側と見なすことで、変圧器理論を応用した解析が可能となります。
ただし、変圧器が静的な電磁エネルギー伝達装置であるのに対し、誘導電動機は電気エネルギーを回転運動エネルギーへと変換する動的システムです。また、変圧器では一次・二次の周波数が同一ですが、誘導電動機においては回転子の運動により、固定子電流と回転子電流の周波数に差異が生じるという本質的な違いがあります。
回転子停止時における誘導起電力
回転子が静止状態にある場合、固定子巻線が作る回転磁界は、同期速度で回転子導体を切ります。このとき、変圧器と完全に同じ電磁誘導現象が発生し、固定子には一次誘導起電力 \(E_1\)、回転子には二次誘導起電力 \(E_2\) が各相に誘起されます。
回転子動作時における誘導起電力
実際の運転状態において、回転子が速度 \(n\) [min⁻¹]で回転している場合を考えます。回転磁界の同期速度 \(n_s\) に対する回転子の相対速度は \(n_s-n=sn_s\) となります。ここで \(s\) はすべりを表します。この相対速度の比率により、運転時の二次誘導起電力 \(E_2'\) [V]は静止時の \(s\) 倍に減少し、同様に回転子電流の周波数 \(f_2\) [Hz]もすべりに比例した値となります。
ここで、\(f_1\) は一次巻線への電源周波数、\(f_2\) すなわち \(sf_1\) は回転子巻線を流れる電流の周波数で「すべり周波数」と呼ばれます。
二次電流の導出
すべり \(s\) で運転される誘導電動機において、回転子巻線の各相は抵抗 \(r_2\) [Ω]と漏れリアクタンス \(x_2\) [Ω]を持ちます。動作時の二次誘導起電力が \(sE_2\) [V]となり、リアクタンスもすべり周波数に比例して \(sx_2\) [Ω]に変化することから、オームの法則により二次電流 \(I_2\) [A]が決定されます。
この式を変形すると:
\[I_2 = \frac{E_2}{\sqrt{\left(\frac{r_2}{s}\right)^2 + x_2^2}}\]この変形式から、運転時の回転子回路は、あたかも抵抗が \(r_2\) から \(\frac{r_2}{s}\) に増加したかのように振る舞うことが分かります。増加分 \(R = \frac{r_2}{s} - r_2 = r_2\frac{1-s}{s}\) は、機械的負荷を電気的に表現した等価負荷抵抗として解釈されます。
一次電流の関係
回転子に流れる二次電流 \(I_2\) [A]は、それ自身の起磁力を発生させます。この起磁力は固定子の主磁束を減少させる方向に作用するため、固定子側では磁束を維持するための補償電流(一次負荷電流)\(I_1'\) [A]が追加的に流れます。巻数比を \(\alpha\) とすると、アンペアターンの平衡条件から次の関係が導かれます。
実際の一次電流 \(I_1\) [A]は、磁束を確立するための励磁電流 \(I_0\) [A]と、負荷による一次負荷電流 \(I_1'\) [A]のベクトル和として表されます。すなわち \(\dot{I}_1 = \dot{I}_0 + \dot{I}_1'\) という関係が成立します。
2. 等価回路の理解
理想的な三相誘導電動機
すべての巻線抵抗と漏れインダクタンスがゼロであり、完全な磁気結合を持つ仮想的な誘導電動機を「理想的な三相誘導電動機」と定義します。この理想機は、一次側の電気的状態を損失なく二次側へ伝達する完全な電磁結合装置として機能します。
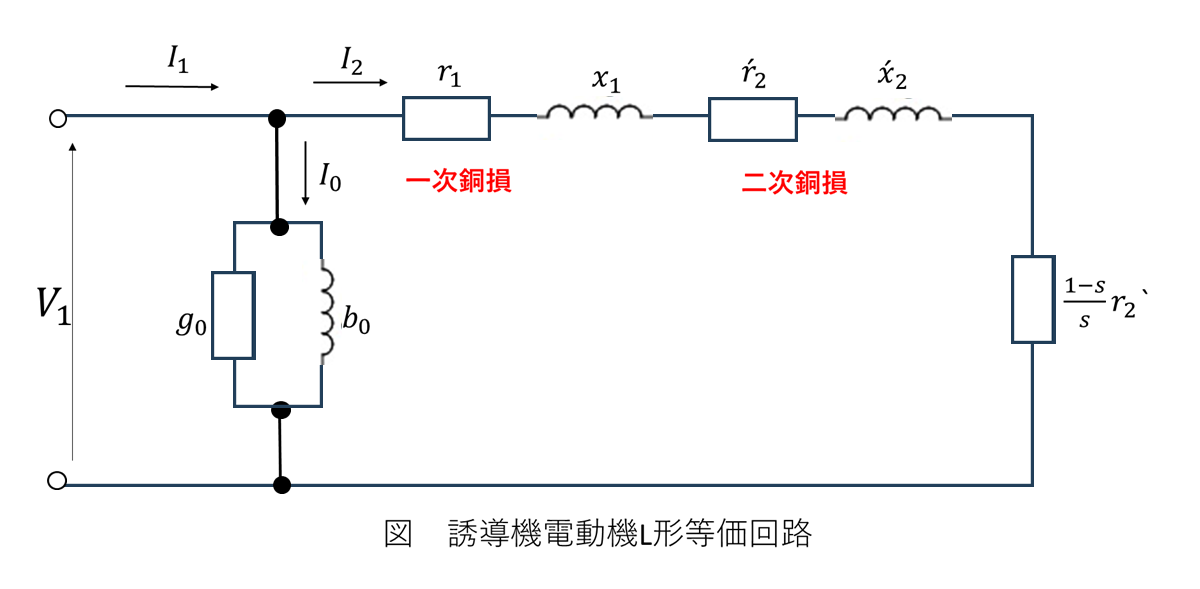
現実の誘導電動機では、巻線の導体抵抗による損失と、完全に結合しない漏れ磁束によるインダクタンス成分が必ず存在します。これらの非理想的要素を理想機の外部に配置することで、実機の特性を正確に表現する等価回路モデルが構築されます。具体的には、固定子側に抵抗 \(r_1\) [Ω]と漏れリアクタンス \(x_1\) [Ω]、回転子側に抵抗 \(r_2\) [Ω]と漏れリアクタンス \(x_2\) [Ω]を接続した回路として表現されます。
励磁回路
負荷抵抗 \(R\) を短絡(すべり1の状態)として一次側に電圧を印加したときに流れる電流が励磁電流 \(\dot{I}_0\) です。この電流は主磁束を形成する磁化成分と、鉄心内での損失に対応する有効成分から構成されます。
\(\dot{I}_0\) [A]:励磁電流
\(g_0\) [S]:励磁コンダクタンス
\(b_0\) [S]:励磁サセプタンス
\(\dot{Y}_0\) [S]:励磁アドミタンス
L型等価回路の構成
励磁要素を含む完全な等価回路は、誘導電動機の各相の電気的挙動を表現します。解析の際は、理想変圧器部分を除去し、純粋な電気回路として取り扱うことで、通常の回路理論を適用できます。
図中の各要素において、\(I_1\)は固定子電流、\(I_2\)は回転子電流、\(I_0\)は励磁電流を示します。特に、回路末端の抵抗\(\frac{1-s}{s}r_2\)は、電動機が行う機械的仕事を電気的に表現する重要な要素です。
各相における二次側の電力収支を考察すると、二次入力 \(P_2'\) [W]、二次巻線での抵抗損 \(P_{c2}'\) [W]、機械的出力 \(P_0'\) [W]の間に、以下の重要な関係式が成立します。
機械的出力 \(P_0'\) [W]は、等価負荷抵抗での消費電力として次のようにも表現できます。
上式で \(R\) [Ω]は機械的出力に対応する等価抵抗であり、全体の等価抵抗 \(\frac{r_2}{s}\) [Ω]は、実際の回転子抵抗 \(r_2\) [Ω]と機械負荷分 \(R\) [Ω]の和として理解されます。
簡略等価回路における諸量の計算
実用的な計算では、励磁分岐を電源端に移動させた簡略等価回路が広く採用されています。この近似により計算が大幅に簡素化される一方、工学的に十分な精度が保たれます。示された回路は一相分を表しており、三相システム全体の諸量を求めるには、各相の値を3倍する必要があります。
一次負荷電流:
\[I_1' = \frac{V_1}{\sqrt{\left(r_1 + \frac{r_2'}{s}\right)^2 + (x_1 + x_2')^2}} \text{ [A]}\]励磁電流:
\[I_0 = V_1\sqrt{g_0^2 + b_0^2} \text{ [A]}\]一次入力:
\[P_1 = P_i + P_{c1} + P_{c2} + P_0 = 3V_1 I_1 \cos\theta_1 = \sqrt{3}V_n I_l \cos\theta_1\]二次入力:
\[P_2 = P_{c2} + P_0 = \frac{P_0}{1-s} = 3{I_1'}^2 \frac{r_2'}{s}\]二次入力、二次銅損、二次出力の比:
\[P_2 : P_{c2} : P_0 = 1 : s : (1-s)\]鉄損:
\[P_i = 3V_1 I_{0w} = 3V_1^2 g_0\]一次銅損・二次銅損:
\[P_{c1} = 3{I_1'}^2 r_1 \text{ [W]}\] \[P_{c2} = 3{I_1'}^2 r_2' = sP_2\]出力:
\[P_0 = 3{I_1'}^2 R' = 3{I_1'}^2 \left(\frac{1-s}{s}\right)r_2' = (1-s)P_2 = \omega T\]同期ワット:
\[P_2 = \frac{2\pi n_s T}{60}\]二次効率:
\[\eta_0 = \frac{P_0}{P_2} = \frac{(1-s)P_2}{P_2} = 1-s\]電動機効率:
\[\eta = \frac{P_0}{P_1}\]二次入力は工学的に「同期ワット」と称されます。この名称は、計算式において実際の回転速度 \(n\) ではなく同期速度 \(n_s\) を用いることに由来します。この特徴的な表現は、誘導電動機の理論において重要な概念です。
回転子抵抗\(r_2 = 0.02\)Ω、すべり\(s = 0.05\)の誘導電動機について、等価抵抗と機械出力対応抵抗を求めよ。
解答:
等価抵抗:
\[\frac{r_2}{s} = \frac{0.02}{0.05} = 0.4 \, \mathrm{[\Omega]}\]機械出力対応抵抗:
\[r_2\frac{1-s}{s} = 0.02 \times \frac{1-0.05}{0.05} = 0.02 \times 19 = 0.38 \, \mathrm{[\Omega]}\]3. 回路定数の求め方
等価回路を用いた誘導電動機の解析において、回路定数の正確な把握は不可欠です。これらの定数は、国際的に標準化された試験手法により決定されます。主要な試験として、無負荷運転による励磁特性の測定、回転子を固定した状態での短絡特性の測定、および巻線の直流抵抗測定が実施されます。各試験は特定の物理現象を際立たせる条件で行われ、得られたデータから系統的に回路定数が導出されます。
無負荷試験
定格電圧を印加して電動機を無負荷で運転する試験により、励磁回路の特性が明らかになります。無負荷状態ではすべりがほぼゼロに近く(典型的には1%未満)、回転子電流は極めて微小となります。このため、測定される電流はほぼ励磁電流のみとなり、励磁回路パラメータの抽出が可能となります。
測定される無負荷電力には、磁気回路での鉄損と回転部の機械損が含まれます。電流測定値から励磁リアクタンス\(x_0\)が算出され、電力測定値を解析することで励磁抵抗\(r_0\)が決定されます。これらのパラメータは、電動機の磁気特性を表す基本的な定数となります。
拘束試験(短絡試験)
機械的に回転子を完全に固定した状態で、定格電流が流れる程度の低電圧を印加する試験です。すべりが1となるこの条件では、回転子側のインピーダンスが最小値を示し、漏れインピーダンスの影響が顕著に現れます。低電圧のため励磁電流は無視でき、測定電流は実質的に負荷電流成分のみとなります。
この試験で得られる電力は、固定子および回転子の巻線抵抗による損失が主体です。電圧、電流、電力の測定値から、一次・二次の合成抵抗と合成リアクタンスが算出されます。ただし、これらを個別の回路定数に分離するには、設計情報や経験的な配分比率を用いる必要があります。
直流抵抗測定
精密な抵抗測定により、固定子巻線の純抵抗成分\(r_1\)を決定します。ホイートストンブリッジや高精度デジタル抵抗計を用いて、室温での抵抗値を測定した後、実運転温度への換算を行います。銅導体の温度係数(0.393%/℃)を用いた温度補正により、実使用条件での正確な抵抗値が得られます。
かご型回転子では直接的な抵抗測定が困難なため、拘束試験の結果から間接的に回転子抵抗を推定します。一方、巻線型回転子の場合は、スリップリングを介して直接測定することも可能です。いずれの場合も、温度補正と接触抵抗の考慮が重要となります。
等価回路定数の算出手順
試験データから回路定数を導出する体系的な手順が確立されています。まず直流測定により固定子抵抗\(r_1\)を確定し、次に無負荷試験データから励磁パラメータ\(r_0\)、\(x_0\)を算出します。最後に、拘束試験の結果と既知の\(r_1\)を用いて、回転子側の定数\(r_2\)と漏れリアクタンス\(x_1\)、\(x_2\)を決定します。
ここで、\(V_1\):印加電圧、\(I_0\):無負荷電流、\(P_0\):無負荷電力
三相誘導電動機の無負荷試験で、線間電圧200V、線電流5A、三相電力600Wが測定された。固定子抵抗\(r_1 = 0.5\)Ωのとき、励磁回路定数を求めよ。
解答:
相電圧:\(V_1 = \frac{200}{\sqrt{3}} = 115.5\)V
相電流:\(I_0 = 5\)A
一相分電力:\(P_{0,1} = \frac{600}{3} = 200\)W
\begin{aligned} r_0 &= \frac{V_1^2}{P_{0,1} - I_0^2 r_1} \\[10pt] &= \frac{115.5^2}{200 - 5^2 \times 0.5} \\[10pt] &= \frac{13340}{200 - 12.5} = \frac{13340}{187.5} = 71.1 \, \mathrm{[\Omega]} \end{aligned}試験結果の検証と調整
導出された回路定数の妥当性は、実運転データとの照合により確認されます。計算により予測される効率、力率、すべり等の特性値が実測値と著しく乖離する場合、定数の再検討が必要です。運転温度や電源周波数の変動による影響も考慮し、必要に応じて補正係数を適用します。
回路定数は電動機の経年変化や運転環境により変動するため、定期的な再測定が推奨されます。同型機の測定データを統計的に処理することで、機種固有の標準定数を確立することも一般的な実務です。このような標準化により、設計段階での特性予測精度が向上します。
- 無負荷試験:励磁回路定数(\(r_0\)、\(x_0\))を求める
- 拘束試験:漏れ定数(\(r_2\)、\(x_1\)、\(x_2\))を求める
- 直流測定:固定子抵抗(\(r_1\))を正確に測定
- 温度補正:抵抗値の温度依存性を考慮
- 検証:計算値と実測値の整合性確認
- 回転起磁力:三相系統で一定強度の回転磁界を発生
- すべり周波数:\(f_r = sf\)、回転子電流の周波数
- 等価回路:T型回路で電動機特性を表現
- 回転子等価抵抗:\(\frac{r_2}{s} = r_2 + r_2\frac{1-s}{s}\)
- 試験方法:無負荷試験、拘束試験、直流抵抗測定
- 定数算出:各試験結果から等価回路定数を決定
- すべり周波数:\(f_r = sf\)の計算問題頻出
- 等価抵抗分解:機械出力対応部分の理解
- 試験の目的:各試験で何を求めるかを整理
- 無負荷試験:励磁定数の算出手順
- 拘束試験:漏れ定数の概念と測定法
- 等価回路:簡略回路での特性計算
さらに詳しく学びたい方へ
本ページでは誘導電動機の基本原理から等価回路まで教科書的に体系立てて解説していますが、より実践的な視点で誘導電動機を理解したい方には、応用例や演習問題を豊富に含んだ解説ページもご用意しています。
📚 【第三種電気主任技術者試験】誘導電動機の完全解説 - 構造から特性・制御まで
身近な応用例、詳細な演習問題、過去問解説を含む実践的学習ページ
第3節 三相誘導電動機の特性
1. 電流と力率
三相誘導電動機の電流と力率は、負荷の変化に応じて大きく変化する重要な特性です。無負荷時から全負荷時にかけて、電流は磁化電流から負荷電流まで連続的に変化し、力率も大きく改善されます。これらの特性を理解することは、電動機の効率的な運用と電力系統への影響を評価するために不可欠です。また、力率改善の必要性や方法を検討する上でも重要な知識となります。
固定子電流の構成
固定子に流れる電流は、大きく「磁化電流」と「負荷電流」に分けられます。磁化電流は主磁束を作るために必要な電流で、負荷に無関係にほぼ一定値を示します。一方、負荷電流は回転子電流に対応する電流で、負荷トルクに比例して増加します。全固定子電流は、これら二つの電流のベクトル合成で表されます。
磁化電流は主として無効電流であり、電動機の力率を低下させる主要因となります。高効率電動機では、磁化電流を小さくするために磁気回路の設計が最適化されています。負荷電流は有効電流成分と無効電流成分を含み、その比率は回転子回路のインピーダンス特性によって決まります。
電流の負荷特性
誘導電動機の電流は、負荷の増加とともに増加しますが、その関係は線形ではありません。軽負荷域では磁化電流の割合が大きく、電流の増加率は負荷の増加率より小さくなります。中負荷域では負荷電流が支配的となり、電流は負荷にほぼ比例して増加します。重負荷域では、滑りの増加により回転子抵抗成分が相対的に減少し、電流の増加率が再び大きくなります。
始動時の電流は特に大きく、定格電流の5~7倍に達することがあります。これは回転子が静止しているため滑りが1となり、回転子インピーダンスが最小となるためです。この大きな始動電流は、電源系統への影響や電動機の発熱の原因となるため、大容量機では始動電流制限装置が必要になります。
ここで、\(r_2'\)、\(x_2'\)は固定子換算値
力率の特性
誘導電動機の力率は、負荷率に大きく依存します。無負荷時の力率は0.1~0.2程度と極めて低く、これは電流の大部分が磁化電流(無効電流)であるためです。負荷が増加するにつれて有効電流成分が増加し、力率は改善されます。定格負荷付近で最良の力率(通常0.8~0.9)を示し、過負荷域では再び悪化する傾向があります。
力率の負荷特性は、電動機の効率的な運用を考える上で重要です。軽負荷運転では力率が著しく悪化するため、複数台運転の場合は適切な台数制御が必要です。また、力率改善コンデンサの容量選定においても、運転負荷率を考慮する必要があります。
三相誘導電動機の入力電力が8kW、線電流が25A、線間電圧が200Vのとき、力率を求めよ。
解答:
\begin{aligned} \cos\phi &= \frac{P}{\sqrt{3}VI} \\[10pt] &= \frac{8000}{\sqrt{3} \times 200 \times 25} \\[10pt] &= \frac{8000}{8660} = 0.924 \end{aligned}無効電力と力率改善
誘導電動機は多量の無効電力を消費します。この無効電力は主として磁化に必要なものですが、電力系統の力率を悪化させ、送電効率を低下させます。大容量の誘導電動機が多数運転される工場では、力率改善が重要な課題となります。
力率改善の方法としては、進相コンデンサの設置が最も一般的です。コンデンサは遅れ無効電力を補償し、系統から見た力率を改善します。ただし、コンデンサ容量が過大だと進み力率となり、電圧上昇や系統不安定の原因となるため、適切な容量選定が重要です。
2. 入出力と損失
誘導電動機のエネルギー変換過程では、電気入力から機械出力への変換において各種の損失が発生します。これらの損失を正確に理解することは、効率計算、発熱評価、および省エネルギー対策を検討する上で極めて重要です。損失の種類と発生メカニズムを把握することで、高効率運転の方策や適切な冷却設計が可能になります。
損失の分類と特徴
誘導電動機の損失は、「固定損失」と「可変損失」に大別されます。固定損失は負荷に無関係にほぼ一定の損失で、鉄損と機械損が含まれます。可変損失は負荷に依存する損失で、主として銅損(固定子銅損と回転子銅損)がこれに該当します。これらの損失の大きさとバランスが、電動機の効率特性を決定します。
鉄損は固定子鉄心で発生し、ヒステリシス損失とうず電流損失から構成されます。これらは磁束密度の2乗と周波数に比例するため、定格運転では一定値となります。機械損は軸受摩擦損と風損から構成され、回転速度にほぼ依存します。通常運転では滑りが小さいため、機械損もほぼ一定と見なせます。
銅損の特性
銅損は電流の2乗に比例する損失で、負荷の増加とともに急激に増加します。固定子銅損は固定子電流の2乗に比例し、回転子銅損は回転子電流の2乗に比例します。回転子銅損は滑りにも依存し、滑りが大きいほど損失も大きくなります。これが誘導電動機で滑りを小さく保つことが重要な理由の一つです。
回転子銅損と機械出力の関係は、等価回路の解析から明らかになります。回転子で発生する全電力を\(P_2\)とすると、そのうち滑り\(s\)の割合が回転子銅損となり、残りの\((1-s)\)の割合が機械出力となります。この関係式\(P_{cu2} = sP_2\)、\(P_m = (1-s)P_2\)は、誘導電動機の基本的な電力関係を表しています。
ここで、\(P_2\):回転子で発生する全電力
効率の計算と特性
効率は出力と入力の比として定義され、損失が小さいほど高効率となります。誘導電動機の効率は負荷率に依存し、通常75~100%負荷で最高効率を示します。軽負荷では鉄損と機械損(固定損失)の割合が大きくなり効率が低下し、重負荷では銅損(可変損失)の急激な増加により効率が低下します。
現代の高効率誘導電動機では、材料の改良、設計の最適化、製造精度の向上により、定格効率90%以上が達成されています。プレミアム効率モータ(IE3)では95%以上、スーパープレミアム効率モータ(IE4)では96%以上の効率が実現されています。これらの高効率化は、省エネルギーと運転コスト削減に大きく貢献しています。
入力電力12kW、機械出力10.5kWの三相誘導電動機について、効率と全損失を求めよ。
解答:
効率:
\[\eta = \frac{P_{out}}{P_{in}} \times 100 = \frac{10.5}{12.0} \times 100 = 87.5 \, \mathrm{[\%]}\]全損失:
\[P_{loss} = P_{in} - P_{out} = 12.0 - 10.5 = 1.5 \, \mathrm{[kW]}\]漂遊負荷損失
従来の損失分類に加えて、近年注目されているのが「漂遊負荷損失」です。これは高調波磁束による追加損失で、負荷に依存して変化します。インバータ駆動時には、PWM制御による高調波成分により、この損失が増加する傾向があります。現代の効率評価では、この漂遊負荷損失を含めた総合的な損失評価が重要になっています。
3. トルクの特性
誘導電動機のトルク特性は、滑りとの関係で表現される重要な性能指標です。始動から定格運転まで、滑りの変化に応じてトルクは特徴的な曲線を描きます。この特性を理解することは、電動機の選定、始動方法の検討、負荷との適合性評価において不可欠です。また、最大トルクや始動トルクなどの重要な定格値も、この特性曲線から読み取ることができます。
トルク-滑り特性の基本形
誘導電動機のトルクは、簡易等価回路から導出される基本式で表されます。この式は滑り\(s\)の関数として表現され、分子が\(s\)に比例し、分母が\(s\)を含む2次式となる有理関数の形をとります。この結果、トルク-滑り特性は特徴的な山形の曲線となり、最大トルクを与える最適滑りが存在します。
ここで、\(r_2'\)、\(x_2'\)は固定子換算値
トルク-滑り特性の形状
トルク-滑り特性は特徴的な山形の曲線となります。滑りが小さい領域(通常運転域)ではトルクは滑りにほぼ比例し、滑りが大きい領域(始動域)ではトルクは滑りに反比例します。この二つの領域の境界付近で最大トルクが発生します。
小滑り域では、回転子抵抗\(r_2'\)が支配的となり、\(T \propto s\)の関係が成り立ちます。この領域は通常運転域であり、負荷の増加に対してトルクが比例的に増加する安定した特性を示します。大滑り域では、回転子リアクタンス\(x_2'\)が支配的となり、\(T \propto \frac{1}{s}\)の関係が成り立ちます。この領域は始動域であり、滑りが大きいほどトルクが小さくなります。
始動トルクと定格トルク
始動トルクは滑り\(s = 1\)のときのトルクで、電動機が負荷を始動できるかどうかを決める重要な値です。一般的に始動トルクは定格トルクの1.5~2.5倍程度ですが、これは電動機の設計により大きく変わります。高始動トルクが必要な用途では、回転子スロット形状の工夫や二重籠型構造などが採用されます。
定格トルクは定格出力時のトルクで、負荷との適合性を評価する基準となります。定格トルクでの滑りは通常3~5%程度で、この範囲で効率的な運転が可能です。負荷トルクが定格トルクを超えると滑りが急激に増加し、効率が悪化するとともに発熱も増加します。
4. 最大トルク・最大出力
最大トルクは誘導電動機の重要な性能指標の一つです。最大トルクとそれを発生する滑り(最大トルク滑り)は、等価回路定数から理論的に求めることができます。最大トルクは電圧の2乗に比例し、周波数に反比例する特性を持ちます。この特性は、電圧変動や周波数変動が電動機性能に与える影響を評価する上で重要です。
最大トルクの導出
最大トルクを求めるには、トルクの基本式を滑りで微分し、それを零とおいて最大トルク滑りを求めます。最大トルク滑りは、回転子抵抗と回転子リアクタンスの比で決まり、\(s_{max} = \frac{r_2'}{x_2'}\)の関係があります。この滑りでのトルクが最大トルクとなります。
最大トルクの特性
最大トルクは電圧の2乗に比例するため、電圧降下により大幅に減少します。例えば、電圧が10%低下すると最大トルクは約19%減少します。これは電動機の始動や過負荷耐量に大きな影響を与えるため、適切な電圧管理が重要です。
最大トルクは周波数に反比例するため、周波数が低下すると最大トルクは増加します。ただし、周波数の変化は同期速度にも影響するため、実際の運転特性は複雑になります。インバータ制御では、V/f一定制御により磁束を一定に保ち、トルク特性を維持します。
最大出力と効率
最大出力は最大トルクと同じ滑りでは発生しません。出力は\(P = T \times \omega\)で表され、トルクと回転速度の積となるため、最大出力点は最大トルク点より小さな滑りで発生します。一般的に最大出力は定格出力の2~3倍程度で、短時間であれば過負荷運転が可能です。
定格電圧200Vで運転している誘導電動機を180Vで運転する場合、最大トルクは何倍になるか。
解答:
\begin{aligned} \frac{T_{max,180V}}{T_{max,200V}} &= \left(\frac{180}{200}\right)^2 \\[10pt] &= (0.9)^2 = 0.81 \end{aligned}最大トルクは0.81倍(19%減少)となる。
5. 比例推移
誘導電動機の各特性は相互に関連しており、一つの特性が変化すると他の特性も連動して変化します。例えば、電圧が変化すると、トルクは電圧の2乗に比例して変化し、電流や滑りも変化します。これらの比例関係を理解することで、運転条件の変化に対する影響を予測することができます。
電圧変化の影響
電圧変化は誘導電動機の特性に大きな影響を与えます。電圧が変化すると、トルクは電圧の2乗に比例して変化し、最大トルクも同様に変化します。始動電流は電圧に比例しますが、運転電流は負荷との関係で決まるため、複雑な変化を示します。
電圧低下により最大トルクが減少すると、同一負荷に対して滑りが増加し、効率が悪化します。逆に電圧が過大になると、磁化電流が増加し、力率が悪化します。適正電圧での運転が効率と性能の両面で重要です。
- トルク:電圧の2乗に比例
- 最大トルク:電圧の2乗に比例
- 始動電流:電圧に比例
- 滑り:電圧の2乗に反比例
周波数変化の影響
周波数変化も電動機特性に大きな影響を与えます。周波数が変化すると同期速度が比例的に変化し、これに伴って回転速度も変化します。トルクは周波数の2乗に反比例する傾向がありますが、実際には磁束の変化も関与するため複雑です。
インバータ制御では、周波数と電圧を比例制御(V/f一定制御)することで、磁束を一定に保ち、トルク特性を維持します。これにより、広い速度範囲で安定した運転が可能になります。
負荷変動に対する応答
誘導電動機は負荷変動に対して自動的に適応する特性を持ちます。負荷が増加すると滑りが増加し、これにより回転子電流が増加してトルクが増大します。この自己調節作用により、負荷の要求に自動的に応答します。
ただし、過大な負荷変動は滑りの急激な変化を引き起こし、効率の悪化や発熱の増加につながります。適切な容量選定と運転管理により、効率的な運転を維持することが重要です。
- 力率特性:負荷率に依存、定格負荷付近で最良
- 損失分類:固定損失(鉄損・機械損)と可変損失(銅損)
- 回転子損失:\(P_{cu2} = sP_2\)、\(P_m = (1-s)P_2\)
- トルク特性:滑りに対して山形の特性曲線
- 最大トルク:電圧の2乗に比例、周波数に反比例
- 比例推移:電圧変化に対する各特性の変化
- 力率計算:\(\cos\phi = \frac{P}{\sqrt{3}VI}\)の公式
- 回転子電力配分:滑りによる損失と出力の関係
- トルク式:簡易等価回路からのトルク導出
- 最大トルク:電圧依存性の計算問題
- 効率計算:各種損失を含めた効率評価
- 特性変化:運転条件変化に対する影響評価
第4節 三相誘導電動機の運転と制御
1. 始動の方法
三相誘導電動機の始動は、大きな始動電流への対策が主要な課題となります。始動時は回転子が静止しているため滑りが1となり、回転子インピーダンスが最小となって大電流が流れます。この始動電流は定格電流の5~7倍に達し、電源系統への影響、電動機の発熱、機械的衝撃などの問題を引き起こします。適切な始動方法の選択により、これらの問題を解決し、安全で効率的な始動が可能になります。
直入始動
直入始動は、電動機を定格電圧で直接始動する最も簡単な方法です。始動装置が不要で経済的ですが、大きな始動電流が流れるため、小容量機(通常3.7kW以下)に限定されます。始動電流は定格電流の5~7倍、始動トルクは定格トルクの1.5~2.5倍程度となります。電源容量に対して電動機容量が小さく、始動電流による電圧降下が問題とならない場合に適用されます。
直入始動の利点は、構造が簡単で保守が容易なことです。また、最大の始動トルクが得られるため、重負荷の始動にも対応できます。欠点は、始動電流が大きいため電源系統への影響が大きく、大容量機では使用できないことです。また、始動時の機械的衝撃も大きくなります。
Y-Δ(スター・デルタ)始動
Y-Δ始動は、始動時にスター接続で運転し、一定速度に達した後にデルタ接続に切り替える方法です。スター接続時の線間電圧は相電圧と等しく、デルタ接続時の\(\frac{1}{\sqrt{3}}\)となるため、始動電流を\(\frac{1}{3}\)に、始動トルクも\(\frac{1}{3}\)に低減できます。この方法は中容量機(5.5~75kW程度)でよく使用され、始動電流制限効果が大きいのが利点です。
Y-Δ始動の欠点は、切り替え時に瞬間的な電流および機械的衝撃が発生することです。また、スター接続時のトルクが低いため、重負荷の始動には適しません。電動機は通常運転時にデルタ接続となるよう巻線が設計されている必要があります。
スター接続時は電流・トルクともに1/3に低減
リアクトル始動
リアクトル始動は、始動時に電動機とリアクトルを直列接続し、一定速度に達した後にリアクトルを短絡する方法です。リアクトルによる電圧降下で電動機印加電圧を下げ、始動電流を制限します。電圧がn倍になると電流はn倍、トルクは\(n^2\)倍となるため、適度な始動電流制限と始動トルクの確保が可能です。
リアクトル始動の利点は、Y-Δ始動のような切り替えショックがないことです。また、負荷の大きさに応じてリアクトルのタップを切り替えることで、始動特性の調整が可能です。欠点は、リアクトルが大型で高価なことと、始動中に無効電力を消費することです。
抵抗始動
抵抗始動は、始動時に抵抗器を電動機と直列接続し、段階的に抵抗値を減らして加速する方法です。主として巻線型誘導電動機の回転子回路に用いられ、始動電流の制限と始動トルクの向上を同時に実現できます。回転子抵抗を増加させることで、最大トルクを発生する滑りを大きくし、始動時により大きなトルクを得ることができます。
抵抗始動では、始動抵抗を段階的に短絡することで滑らかな加速が可能です。各段での抵抗値を適切に選定することで、理想的な始動特性を実現できます。ただし、始動抵抗での電力消費が大きく、効率が悪化するという欠点があります。
直入始動電流が150Aの三相誘導電動機をY-Δ始動する場合の始動電流を求めよ。
解答:
\begin{aligned} I_{Y始動} &= \frac{1}{3} \times I_{直入} \\[10pt] &= \frac{1}{3} \times 150 \\[10pt] &= 50 \, \mathrm{[A]} \end{aligned}ソフトスタータ
ソフトスタータは、サイリスタを用いて印加電圧を徐々に上昇させる電子式始動装置です。始動時に低電圧から開始し、時間の経過とともに電圧を上昇させることで、滑らかな始動が可能です。電流やトルクの制限値を任意に設定でき、負荷に応じた最適な始動制御が実現できます。
ソフトスタータの利点は、機械的接点がないため保守が容易で、始動特性を細かく調整できることです。また、停止時の制動制御も可能です。欠点は、サイリスタによる高調波の発生と、装置コストが高いことです。
2. 速度制御のやり方
誘導電動機の速度制御は、同期速度の制御と滑りの制御に大別されます。同期速度は電源周波数と極数によって決まるため、周波数制御や極数変換による制御が可能です。滑りの制御は回転子回路の制御によって行われ、主として巻線型誘導電動機で用いられます。現代では、インバータによる周波数制御が最も一般的で効率的な速度制御方法となっています。
周波数制御(インバータ制御)
周波数制御は、電源周波数を変化させることで同期速度を制御し、電動機の回転速度を変える方法です。インバータ(可変周波数電源装置)を用いて、商用電源の固定周波数を任意の周波数に変換します。周波数に比例して同期速度が変化するため、広い速度範囲での連続的な速度制御が可能です。
周波数制御では、周波数の変化に応じて電圧も比例制御する「V/f一定制御」が基本となります。これにより、磁束を一定に保ち、トルク特性を維持できます。現代のインバータでは、ベクトル制御や直接トルク制御などの高度な制御方式により、より精密な速度・トルク制御が実現されています。
V/f一定制御の原理
V/f一定制御では、電圧と周波数の比を一定に保つことで、電動機の磁束を一定に維持します。磁束は電圧を周波数で除した値に比例するため、この比を一定にすることで定トルク特性が得られます。低速域では電圧降下補償を行い、高速域では電圧制限により弱め磁束制御を行います。
電圧と周波数の比を一定に保つことで磁束を一定に維持
極数変換制御
極数変換制御は、固定子巻線の接続を切り替えることで極数を変化させ、同期速度を段階的に変える方法です。例えば、4極と6極を切り替えることで、50Hz電源において1500min⁻¹と1000min⁻¹の2段階速度制御が可能です。構造が比較的簡単で確実性が高く、ファンやポンプなどの速度段階制御に用いられます。
極数変換の方式には、「定トルク型」と「定出力型」があります。定トルク型は各速度でほぼ同じトルクを発生し、コンベアなどの定トルク負荷に適します。定出力型は各速度でほぼ同じ出力を発生し、工作機械の主軸などの定出力負荷に適します。
4極の誘導電動機を50Hzで運転時の同期速度と、30Hzで運転時の同期速度を求めよ。
解答:
50Hz運転時:
\[N_{s50} = \frac{120 \times 50}{4} = 1500 \, \mathrm{[min^{-1}]}\]30Hz運転時:
\[N_{s30} = \frac{120 \times 30}{4} = 900 \, \mathrm{[min^{-1}]}\]滑り制御(二次抵抗制御)
巻線型誘導電動機では、回転子回路に外部抵抗を挿入することで滑りを制御し、速度を変える方法があります。抵抗値を増加させると滑りが増加し、回転速度が低下します。この方法は連続的な速度制御が可能ですが、挿入抵抗での電力消費により効率が大幅に低下するため、現在では限定的な用途でのみ使用されます。
二次抵抗制御では、回転子回路に液体抵抗器や金属抵抗器を挿入します。液体抵抗器では電解液の濃度により抵抗値を調整し、金属抵抗器では抵抗の短絡段数により調整します。大容量機では、回転子で発生する電力を他の電動機で回収する「シェルビウス結線」なども使用されます。
電圧制御
固定子電圧を変化させることで、トルク特性を変化させて速度制御を行う方法もあります。電圧を下げるとトルクが減少し、軽負荷時には速度が上昇します。しかし、制御範囲が狭く効率も悪化するため、特殊な用途以外では使用されません。現在では、ファンやポンプの省エネルギー制御として、電子式電圧調整器が使用される場合があります。
3. 回転方向の切り替え
三相誘導電動機の回転方向は、三相電源の相順によって決まります。回転方向を逆転させるには、三相のうち任意の二相を入れ替えることで相順を変更します。これにより、回転磁界の回転方向が逆転し、電動機の回転方向も逆転します。この原理は三相誘導電動機の基本的な特徴の一つであり、簡単で確実な逆転制御が可能です。
逆転制御の方法
最も一般的な逆転制御は、電磁接触器を用いた相切り替えです。正転用と逆転用の2組の接触器を設け、それぞれ異なる相順で電動機に接続します。制御回路により、正転または逆転の指令に応じて該当する接触器を動作させます。安全のため、正転と逆転の接触器が同時に動作しないようインターロック回路が必須です。
インターロック回路には、電気的インターロックと機械的インターロックがあります。電気的インターロックでは、一方の接触器が動作中は他方の接触器コイル回路を遮断します。機械的インターロックでは、物理的な機構により同時動作を防止します。高い安全性が要求される用途では、両方を併用します。
プラギング制御
プラギング制御は、運転中の電動機に逆転指令を与えて急速に制動する方法です。逆転接触器を動作させることで強力な制動トルクが得られ、短時間での停止が可能です。ただし、大きな制動電流が流れるため、電動機や電源設備への影響を考慮する必要があります。完全停止のタイミングで電源を遮断する制御も重要です。
プラギング制御では、停止検出装置(零速度リレーなど)を用いて完全停止を検出し、自動的に電源を遮断します。これにより、逆転による過度の加速を防止できます。制動時間は負荷の慣性モーメントと制動トルクにより決まり、適切な設定が重要です。
相順と回転方向の関係
三相交流の相順(R-S-T または U-V-W)により回転磁界の方向が決まります。正相順(R→S→T)では時計回り、逆相順(R→T→S)では反時計回りの回転磁界が発生します。電動機の端子接続により、機械的な回転方向との対応が決まります。
実際の設備では、電動機の取付け方向や負荷機械との結合方法により、電気的回転方向と機械的回転方向の対応が変わります。試運転時に回転方向を確認し、必要に応じて相順を変更する必要があります。
4. 制動(ブレーキ)の方法
誘導電動機の制動方法は、電気的制動と機械的制動に大別されます。電気的制動は電動機自身の電気的特性を利用する方法で、回生制動、プラギング制動、直流制動があります。機械的制動は物理的な摩擦力を利用する方法で、電磁ブレーキや摩擦ブレーキが用いられます。用途に応じてこれらの制動方法を単独または組み合わせて使用します。
回生制動
回生制動は、電動機を発電機として動作させ、運動エネルギーを電気エネルギーに変換して制動する方法です。負荷の慣性により電動機が同期速度以上で回転すると、滑りが負となり発電機動作となります。発生した電力は電源側に回生されるか、制動抵抗で消費されます。エネルギー回収が可能で効率的な制動方法ですが、制動力の制御が複雑です。
回生制動が成立する条件は、電動機の回転速度が同期速度を上回ることです。下り坂を走行する電車や、慣性の大きな負荷を減速する場合に有効です。インバータ制御では、回生電力を直流部のコンデンサに蓄積し、制動抵抗で消費する制動方式が一般的です。
プラギング制動
プラギング制動は、運転中の電動機の相順を逆転させて制動する方法です。回転方向と逆方向の回転磁界により強力な制動トルクが発生し、急速な制動が可能です。制動電流は始動電流より大きくなるため、電動機や電源設備の容量を十分考慮する必要があります。
プラギング制動では、停止点での電源遮断が重要です。停止後も逆転指令が継続すると、電動機が逆方向に回転してしまいます。零速度検出装置や時限制御により、適切なタイミングで電源を遮断する必要があります。
直流制動
直流制動は、交流電源を遮断した後、固定子巻線に直流電流を流して制動する方法です。直流励磁により静止磁界が作られ、回転子の誘導電流との相互作用で制動トルクが発生します。制動力の調整が比較的容易で、確実な制動が得られますが、直流電源が必要で制動中に電力を消費します。
直流制動では、固定子巻線の2相に直流を流すのが一般的です。直流電流の大きさにより制動トルクを調整でき、滑らかな制動が可能です。エレベータや工作機械など、精密な位置決めが必要な用途でよく使用されます。
電磁ブレーキ
電磁ブレーキは、電磁力により摩擦材を制動面に押し付けて制動する機械的制動装置です。通常は電磁コイルの励磁によりブレーキを開放し、消磁時に制動力が働く「無励磁作動型」が安全上の理由で多用されます。停電時や緊急時にも確実に作動し、保持制動力も得られるため、安全性が要求される用途で重要な役割を果たします。
電磁ブレーキには、湿式と乾式があります。湿式は油中で動作するため制動力が安定していますが、保守が複雑です。乾式は保守が容易ですが、摩擦材の摩耗や発熱に注意が必要です。用途に応じて適切な型式を選択します。
- 回生制動:エネルギー回収可能、制御複雑
- プラギング制動:急速制動、大電流発生
- 直流制動:制御容易、電力消費あり
- 電磁ブレーキ:確実作動、保持力あり
慣性モーメント10kg·m²の負荷を持つ電動機を、平均制動トルク50N·mで制動する場合の制動時間を求めよ。初期回転速度は1500min⁻¹とする。
解答:
初期角速度:\(\omega_0 = \frac{2\pi \times 1500}{60} = 157.1\) rad/s
\begin{aligned} t &= \frac{J\omega_0}{T} \\[10pt] &= \frac{10 \times 157.1}{50} \\[10pt] &= 31.4 \, \mathrm{[s]} \end{aligned}- 始動方法:直入、Y-Δ、リアクトル、抵抗始動
- Y-Δ始動:電流・トルクともに1/3に低減
- 速度制御:周波数制御が最も効率的
- V/f制御:磁束一定でトルク特性維持
- 逆転制御:任意の二相入れ替えで相順変更
- 制動方法:電気的制動と機械的制動の組み合わせ
- Y-Δ始動:電流・トルク低減比1/3の計算
- 周波数制御:同期速度の比例関係
- 極数変換:極数と同期速度の関係
- 逆転原理:相順変更による回転方向制御
- 制動分類:各制動方法の特徴と適用
- 始動電流:各始動方法の電流制限効果
第5節 単相誘導電動機と誘導電圧調整器
1. 単相誘導モーターの原理
単相誘導電動機は、単相交流電源で動作する誘導電動機です。家庭用電化製品から小規模な産業機器まで幅広く使用されており、私たちの日常生活に最も身近な電動機の一つです。三相誘導電動機と基本的な動作原理は同じですが、単相電源では回転磁界を直接作ることができないため、特別な工夫が必要になります。この工夫により、簡単な構造で確実な回転を得ることができ、小容量用途での実用性を実現しています。
単相誘導電動機の最大の課題は、単相電流では回転磁界が作れないことです。単相電流により作られる磁界は、その場で強弱を繰り返すだけの「脈動磁界」となります。この脈動磁界は、互いに逆方向に回転する二つの回転磁界の合成として理解することができます。この理論的解釈が、単相誘導電動機の動作解析と設計の基礎となっています。
脈動磁界の分解
脈動磁界は数学的に、互いに逆方向に回転する二つの回転磁界の合成として表現できます。これらの回転磁界はそれぞれ独立に回転子に作用し、それぞれ異なるトルクを発生させます。回転子が静止している時は、両方の回転磁界に対する滑りが等しいため、発生するトルクも等しく、合成トルクは零となります。これが単相誘導電動機に始動トルクがない理由です。
しかし、回転子が回転を始めると、正転方向の回転磁界に対する滑りと逆転方向の回転磁界に対する滑りが異なってきます。これにより、正転トルクと逆転トルクに差が生じ、正味のトルクが発生して回転が継続されます。このメカニズムにより、一度回転を始めた単相誘導電動機は継続して回転することができます。
脈動磁界は正転・逆転する二つの回転磁界の合成
始動の問題と解決方法
単相誘導電動機の根本的な問題は、始動トルクが発生しないことです。この問題を解決するために、人工的に二相状態を作り出して回転磁界を発生させる必要があります。最も一般的な方法は、主巻線とは別に補助巻線を設け、両巻線に位相の異なる電流を流すことです。
位相差を作る方法には、抵抗、コンデンサ、インダクタンスなどの回路素子を利用する方法があります。理想的には90度の位相差が望ましいですが、実際には30~60度程度の位相差でも実用的な始動トルクが得られます。始動完了後は、多くの場合、補助巻線を切り離して単相運転となります。
2. 二相回転磁界のしくみ
単相誘導電動機で回転磁界を作るには、人工的に二相状態を作り出す必要があります。主巻線と補助巻線の二つの巻線を90度の空間角で配置し、これらに位相の異なる電流を流すことで回転磁界を発生させます。位相差は、補助巻線回路にコンデンサや抵抗などの位相シフト素子を挿入することで作り出されます。理想的には90度の位相差が望ましいですが、実際には30~60度程度の位相差でも実用的な回転磁界が得られます。
二相回転磁界の条件
完全な二相回転磁界を得るためには、二つの条件が必要です。第一に、二つの巻線電流の大きさが等しいこと、第二に、両電流の位相差が90度であることです。これらの条件が満たされると、三相系統と同様に一定強度の回転磁界が得られます。実際の単相誘導電動機では、これらの理想条件を完全に満たすことは困難ですが、近似的な二相状態により実用的な性能を実現しています。
理想的な回転磁界発生条件
位相差の作成方法
補助巻線電流の位相を主巻線電流から進めるか遅らせることで位相差を作成します。抵抗を用いる場合は、補助巻線の抵抗分を大きくすることで電流位相を進ませます。コンデンサを用いる場合は、容量性リアクタンスにより電流位相を大きく進ませることができます。インダクタンスを用いる場合は、誘導性リアクタンスにより電流位相を遅らせます。
最も効果的なのはコンデンサを用いる方法で、大きな位相差を作ることができます。また、コンデンサの容量を適切に選定することで、電流の大きさも調整でき、理想的な二相状態に近づけることが可能です。ただし、コンデンサは温度や周波数により特性が変化するため、運転条件を考慮した設計が必要です。
3. 始動方法による分類
単相誘導電動機は、始動方法により「分相始動型」「コンデンサ始動型」「コンデンサ運転型」「シェーディングコイル型」などに分類されます。それぞれ異なる方式で二相状態を作り出し、固有の特性を持ちます。用途に応じてこれらの中から最適な型式を選択することで、効率的で経済的な電動機システムを構築できます。
分相始動型(抵抗分相型)
分相始動型は、補助巻線に抵抗を直列接続することで位相差を作る最も基本的な型式です。補助巻線の抵抗を主巻線より大きくすることで、補助巻線電流の位相を進ませ、主巻線電流との間に位相差を作ります。構造が簡単で製造コストが安いため、小容量の汎用電動機として広く使用されています。
始動完了後は、遠心スイッチにより補助巻線を切り離して単相運転となります。このため、始動トルクは比較的小さく、軽負荷始動用途に適しています。家庭用洗濯機、扇風機、小型ポンプなどに多用されています。運転時の効率は中程度で、騒音も比較的少ないのが特徴です。
コンデンサ始動型
コンデンサ始動型は、補助巻線回路にコンデンサを直列接続する型式です。コンデンサの容量性リアクタンスにより補助巻線電流の位相が大きく進み、主巻線電流との位相差が拡大します。これにより大きな始動トルクが得られ、重負荷の始動が可能になります。始動完了後はコンデンサと補助巻線を切り離し、単相運転となります。
始動用コンデンサには、大容量が必要なため電解コンデンサが使用されます。ただし、電解コンデンサは連続使用に適さないため、始動時のみの短時間使用となります。コンプレッサ、大型ファン、工作機械などの重負荷始動が必要な用途に適用されます。始動トルクは定格トルクの3~4倍程度が得られます。
コンデンサ運転型
コンデンサ運転型は、運転中も常時コンデンサと補助巻線を接続したままにする型式です。運転中も二相状態が維持されるため、トルク脈動が少なく、効率や力率が良好です。運転用コンデンサには連続使用に耐えるフィルムコンデンサやオイルコンデンサが使用されます。
さらに高性能を求める場合は、始動用と運転用の二つのコンデンサを併用する「コンデンサ始動・運転型」も使用されます。この型式では、大容量の始動用コンデンサで大きな始動トルクを得て、小容量の運転用コンデンサで効率的な運転を実現します。エアコンの圧縮機や高級ファンなどに使用されています。
シェーディングコイル型
シェーディングコイル型は、固定子極に短絡環(シェーディングコイル)を設けて回転磁界を作る特殊な型式です。主磁束がシェーディングコイルと鎖交すると、短絡環に電流が誘導され、位相の遅れた磁束が発生します。これにより、極面内で位相の異なる磁束分布が作られ、回転磁界が発生します。
構造が極めて簡単で補助巻線が不要ですが、効率が悪く始動トルクも小さいため、小容量機に限定されます。電動ファン、タイマー、小型ポンプなどの軽負荷用途で使用されています。保守が容易で長寿命という利点があります。
単相100V、0.5kWの誘導電動機で、始動時に主巻線電流と補助巻線電流に90度の位相差を作るために必要なコンデンサ容量を概算せよ。ただし、主巻線のインピーダンスを10Ω、補助巻線の抵抗を15Ωとする。
解答:
90度位相差の条件より、補助巻線のリアクタンス=抵抗
\begin{aligned} X_C &= R_2 = 15 \, \mathrm{[\Omega]} \\[10pt] C &= \frac{1}{2\pi f X_C} = \frac{1}{2\pi \times 50 \times 15} \\[10pt] &= \frac{1}{4712} = 212 \, \mathrm{[\mu F]} \end{aligned}| 型式 | 位相差方法 | 始動トルク | 効率 | 主な用途 |
|---|---|---|---|---|
| 分相始動型 | 抵抗 | 小 | 中 | 軽負荷用 |
| コンデンサ始動型 | 始動用コンデンサ | 大 | 中 | 重負荷始動 |
| コンデンサ運転型 | 運転用コンデンサ | 中 | 良 | 連続運転 |
| シェーディングコイル型 | 短絡環 | 極小 | 悪 | 小容量軽負荷 |
4. 単相誘導電圧調整器
単相誘導電圧調整器は、単相交流電圧を連続的に調整する装置です。変圧器の原理を応用していますが、一次巻線と二次巻線が磁気的に結合するだけでなく、回転子を回転させることで両巻線間の相対位置を変化させ、相互インダクタンスを調整します。これにより、機械的な操作で出力電圧を連続的に変化させることができます。現在では電子式電圧調整器に置き換わっていますが、大容量や特殊用途では今でも使用されています。
構造と動作原理
単相誘導電圧調整器は、円筒形の固定子に一次巻線を配置し、その内側に回転できる円筒形の回転子を設けて二次巻線を配置した構造です。回転子は電動機ではなく手動またはモータ駆動により回転させます。一次巻線と二次巻線の軸が一致している時に最大結合となり、90度ずれた時に最小結合(理論的には零結合)となります。
出力電圧は、入力電圧と巻数比、および結合度(相互インダクタンス)の積で決まります。回転子の回転角度により結合度が連続的に変化するため、出力電圧も連続的に調整できます。調整範囲は通常、定格電圧の0~110%程度です。
ここで、\(\theta\):回転子の回転角度、\(N_1, N_2\):一次・二次巻数
特性と用途
誘導電圧調整器の特長は、機械的接点がなく信頼性が高いことです。また、波形歪みが少なく、負荷の力率にあまり影響されません。一方、構造が複雑で大型になりやすく、調整のために機械的操作が必要という欠点があります。
用途としては、試験用電源、照明調光器、電熱器の温度調整、電動機の速度制御などがありましたが、現在では電子式調整器に置き換わることが多くなっています。ただし、大容量や高信頼性が要求される用途では、今でも使用されています。
調整特性
誘導電圧調整器の調整特性は、回転角度に対してコサイン関数となります。0度から90度の範囲で出力電圧が100%から0%まで変化します。中間の角度では非線形の変化となるため、一定の電圧変化率を得るには回転速度を調整する必要があります。
負荷の種類により出力電圧の安定性が変わります。抵抗負荷では安定していますが、誘導負荷では力率の影響で出力電圧が変動します。このため、用途に応じて補償回路が必要になる場合があります。
5. 三相誘導電圧調整器
三相誘導電圧調整器は、三相交流電圧を調整する装置で、単相型を3台組み合わせたものと、一体型の構造があります。三相負荷の電圧調整に用いられ、特に大容量の電動機始動時の電圧調整や、電熱負荷の温度制御などに使用されています。現代では電子式の三相電圧調整器が主流となっていますが、その動作原理を理解することは重要です。
構造の種類
三相誘導電圧調整器には、「単相型3台組合せ」と「一体型」があります。単相型3台組合せは、単相調整器を3台用いて三相回路を構成する方式で、各相を独立に調整できる利点があります。一体型は、三相分を一つの筐体に収めた構造で、小型化と操作の簡素化が図れます。
一体型では、共通の回転軸に三相分の回転子を取り付け、同期して回転させます。これにより、三相の出力電圧を同じ比率で調整できます。ただし、三相負荷の不平衡や各相の特性差により、完全な平衡調整は困難な場合があります。
調整方式
三相誘導電圧調整器の調整方式には、「同時調整方式」と「個別調整方式」があります。同時調整方式では、3相の回転子を機械的に連結し、同時に回転させて三相の出力電圧を同じ比率で調整します。個別調整方式では、各相を独立に調整でき、不平衡負荷への対応や、各相の微調整が可能です。
同時調整方式は操作が簡単で、三相平衡負荷に適しています。個別調整方式は操作が複雑ですが、柔軟な調整が可能で、特殊な用途に適用されます。実際の選択は、負荷の特性と要求される調整精度により決まります。
現代の三相電圧調整技術
現在の三相電圧調整では、サイリスタを用いた電子式調整器が主流となっています。これらは応答速度が速く、制御が容易で、小型化も可能です。ただし、高調波の発生や力率の悪化などの問題もあり、用途に応じて適切な選択が必要です。
最新の技術では、PWMインバータによる電圧調整も行われています。これにより、高調波の抑制と高効率を同時に実現できます。また、デジタル制御により、複雑な調整パターンや自動制御も可能になっています。
三相誘導電圧調整器の入力電圧が200V、巻数比が1:1.2、回転角が60度の時の出力線間電圧を求めよ。
解答:
\begin{aligned} V_{2L} &= V_{1L} \cdot \frac{N_2}{N_1} \cdot \cos\theta \\[10pt] &= 200 \times 1.2 \times \cos 60° \\[10pt] &= 200 \times 1.2 \times 0.5 \\[10pt] &= 120 \, \mathrm{[V]} \end{aligned}応用と将来展望
三相誘導電圧調整器は、現在でも特定の分野で重要な役割を果たしています。特に、高信頼性が要求される用途や、電子ノイズを嫌う用途では、機械的な調整器が選択される場合があります。また、非常に大容量の場合は、電子式よりも経済的になることもあります。
将来的には、電子式調整器の性能向上により、誘導式調整器の使用はさらに限定的になると予想されます。しかし、その基本原理は変圧器や誘導機の理論的基礎として重要であり、電気工学の教育においても価値のある内容です。
- 利点:連続調整可能、波形歪み少、高信頼性
- 欠点:大型・重量大、機械的操作必要
- 現状:電子式調整器に置き換わり進行中
- 残存用途:大容量、高信頼性要求分野
- 単相電動機:人工的二相状態で回転磁界発生
- 脈動磁界:逆回転する二つの回転磁界の合成
- 始動方式:分相、コンデンサ、シェーディングコイル
- 位相差:補助巻線で主巻線と位相差作成
- 電圧調整器:回転子位置で相互インダクタンス調整
- 調整式:\(V_2 = V_1 \cdot \frac{N_2}{N_1} \cdot \cos\theta\)
- 単相電動機分類:各型式の特徴と用途の違い
- 位相差作成:抵抗・コンデンサによる位相制御
- コンデンサ容量:位相差90度の条件計算
- 電圧調整器原理:相互インダクタンス変化
- 出力電圧計算:回転角度を含む電圧式
- 応用問題:実用計算と特性比較
章末まとめ
学習内容の総合整理
- 回転磁界:三相交流により一定強度の回転磁界発生
- 滑り:同期速度と実回転速度の差、トルク発生の要因
- 自己調節作用:負荷増加→滑り増加→トルク増加
- 構造分類:籠型(簡単・堅牢)、巻線型(制御性良好)
- 同期速度:\(N_s = \frac{120f}{p}\) [min⁻¹]
- 滑り:\(s = \frac{N_s - N}{N_s}\)
- 滑り周波数:\(f_r = sf\) [Hz]
- 回転子電力配分:\(P_{cu2} = sP_2\)、\(P_m = (1-s)P_2\)
- 力率:\(\cos\phi = \frac{P}{\sqrt{3}VI}\)
- トルク基本式:\(T = \frac{3V_1^2}{2\pi f} \cdot \frac{sr_2'}{(r_1 + \frac{r_2'}{s})^2 + (x_1 + x_2')^2}\)
- 始動法:直入、Y-Δ(電流・トルク1/3)、リアクトル
- 速度制御:周波数制御(インバータ)が最効率
- 逆転制御:任意二相の入れ替えで相順変更
- 制動方式:回生、プラギング、直流、電磁ブレーキ
- 単相電動機:人工二相状態による回転磁界発生
試験頻出計算問題
周波数50Hz、6極の三相誘導電動機が950min⁻¹で回転している。同期速度、滑り、滑り周波数を求めよ。
解答:
\begin{aligned} N_s &= \frac{120 \times 50}{6} = 1000 \, \mathrm{[min^{-1}]} \\[10pt] s &= \frac{1000 - 950}{1000} = 0.05 \\[10pt] f_r &= 0.05 \times 50 = 2.5 \, \mathrm{[Hz]} \end{aligned}直入始動電流が180A、始動トルクが150N·mの電動機をY-Δ始動する場合の始動電流と始動トルクを求めよ。
解答:
\begin{aligned} I_{Y始動} &= \frac{1}{3} \times 180 = 60 \, \mathrm{[A]} \\[10pt] T_{Y始動} &= \frac{1}{3} \times 150 = 50 \, \mathrm{[N \cdot m]} \end{aligned}滑り0.04で運転中の誘導電動機の回転子発生電力が8kWの時、回転子銅損と機械出力を求めよ。
解答:
\begin{aligned} P_{cu2} &= s \times P_2 = 0.04 \times 8 = 0.32 \, \mathrm{[kW]} \\[10pt] P_m &= (1-s) \times P_2 = 0.96 \times 8 = 7.68 \, \mathrm{[kW]} \end{aligned}三相誘導電動機の入力が線間電圧200V、線電流30A、三相電力8kWの時、力率を求めよ。
解答:
\begin{aligned} \cos\phi &= \frac{P}{\sqrt{3}VI} \\[10pt] &= \frac{8000}{\sqrt{3} \times 200 \times 30} \\[10pt] &= \frac{8000}{10392} = 0.77 \end{aligned}100V、50Hz単相誘導電動機で、補助巻線抵抗が20Ωの時、90度位相差を作るコンデンサ容量を求めよ。
解答:
90度位相差条件:\(X_C = R = 20\)Ω
\begin{aligned} C &= \frac{1}{2\pi f X_C} \\[10pt] &= \frac{1}{2\pi \times 50 \times 20} \\[10pt] &= \frac{1}{6283} = 159 \, \mathrm{[\mu F]} \end{aligned}電験三種出題傾向と対策
- 同期速度計算:周波数・極数からの基本計算(必出)
- 滑り計算:定義式と滑り周波数の関係
- 回転子電力配分:滑りによる損失と出力の配分
- Y-Δ始動:電流・トルクの1/3低減効果
- 力率計算:三相電力の基本公式応用
- 効率計算:入力・出力・損失の関係
- 回転磁界発生原理:三相電流による回転磁界
- 構造比較:籠型と巻線型の特徴差
- 等価回路:T型回路の各定数の意味
- トルク特性:滑りとトルクの関係曲線
- 始動制御:各始動法の原理と適用
- 単相電動機:各型式の始動原理
- 計算の基本:同期速度、滑り、滑り周波数の関係
- 構造理解:籠型と巻線型の特徴比較
- 等価回路:T型回路と簡易回路の使い分け
- 始動制御:各始動法の電流・トルク制限効果
- 電力配分:回転子電力の損失と出力への配分
- 単相電動機:各型式の始動方式と特徴
- 制御技術:現代のインバータ制御原理
実務への応用
- 製造業:コンベア、ファン、ポンプの駆動
- 建設業:エレベータ、クレーン、空調設備
- 交通機関:電車、エスカレータ、自動扉
- 家庭用品:洗濯機、掃除機、換気扇
- 農林業:灌漑ポンプ、選別機、加工機械
- 高効率モータ:IE3、IE4クラスの普及
- インバータ制御:負荷に応じた最適運転
- 力率改善:進相コンデンサによる無効電力補償
- 適正容量選定:過大容量による効率悪化防止
- 保守管理:定期点検による性能維持
誘導機は産業界の基盤を支える重要な電気機器です。その原理を正しく理解し、適切に運用することで、効率的で安全な電力システムの構築が可能になります。電験三種の学習を通じて得られた知識は、実務において必ず役立つものです。