【第三種電気主任技術者試験】誘導電動機の完全解説 - 構造から特性・制御まで

1. イントロダクション

工場の生産ラインや建物の空調設備、エレベーターなど、私たちの生活を支える様々な場所で「誘導電動機」は使われています。誘導電動機は構造が簡単で堅牢なため、世界中の産業で最も広く使用されている電動機です。

図1: 工場や設備で広く使用される様々な種類の誘導電動機

誘導電動機は電気エネルギーを機械的エネルギーに変換する装置です。その名前の由来は、固定子の巻線に流れる電流によって生じる回転磁界が回転子に電流を「誘導」することから来ています。直流電動機とは異なり、回転子に電力を供給するためのブラシや整流子が不要なため、メンテナンスの手間が少なく長寿命という大きな利点があります。

第三種電気主任技術者試験における重要性
誘導電動機に関する知識は、第三種電気主任技術者試験の「機械」科目において重要な出題分野となっています。特に、誘導電動機の基本原理、特性曲線、始動方法、速度制御方法などは毎年のように出題されています。また、「理論」科目においても、回転磁界や電磁誘導の原理、三相交流に関連して誘導電動機の内容が出題されることがあります。

この学習ページでは、誘導電動機の基本構造から始まり、動作原理、特性、応用まで、第三種電気主任技術者試験の対策として必要な内容を丁寧に解説していきます。実務でも役立つ知識を身につけることを目指しましょう。

2. 誘導電動機の基本構造

誘導電動機は主に「固定子（ステータ）」と「回転子（ロータ）」の2つの主要部分から構成されています。それぞれの構造を理解することが、誘導電動機の動作原理を理解する基礎となります。

2.1 固定子（ステータ）の構造

固定子は誘導電動機の外側の静止している部分で、次の要素から構成されています：

固定子鉄心：薄い珪素鋼板を積層した円筒形の構造物で、磁気回路を形成します
固定子巻線：固定子鉄心のスロット（溝）に配置された導線の巻き線で、交流電源が接続されます
固定子フレーム：固定子鉄心を支持し、電動機全体を保護する外枠です

図2: 誘導電動機の固定子の構造と主要部分

固定子巻線は、単相機では主巻線と補助巻線、三相機では120°の位相差を持つ3つの巻線グループで構成されています。これらの巻線に交流電流が流れることで回転磁界が発生し、これが誘導電動機の動作の基本となります。

2.2 回転子（ロータ）の構造

回転子は誘導電動機の内側の回転する部分で、次の要素から構成されています：

回転子鉄心：固定子と同様に珪素鋼板を積層した円筒形の構造物です
回転子巻線：かご形またはスリップリング形の導体から成り、固定子との間の磁気的相互作用によって電流が誘導されます
シャフト（軸）：回転子を支え、発生した機械的トルクを外部機器に伝達します

図3: かご形誘導電動機の回転子の構造と主要部分

回転子と固定子の間には空隙（エアギャップ）があり、機械的な接触なしに磁気的な結合が行われます。このエアギャップは通常、できるだけ小さく設計されていますが、機械的な接触を避けるために十分な間隔が確保されています。

2.3 かご形とスリップリング形

誘導電動機の回転子は、その構造によって主に2種類に分類されます：

かご形回転子	スリップリング形回転子
アルミニウムまたは銅の導体棒を端部で短絡環で結合した「かご」状の構造	回転子に巻線があり、端部がスリップリングを介して外部に接続可能
構造が簡単で堅牢、メンテナンスフリー	回転子回路に外部抵抗を挿入して始動特性や速度制御が可能
始動トルクが比較的小さい	大きな始動トルクが得られる
一般的な用途で広く使用される	特殊な用途や大型機に使用される

図4: かご形回転子（左）とスリップリング形回転子（右）の構造比較

かご形回転子の構造
かご形回転子（スクイレルケージ型）は、アルミニウムまたは銅の導体棒が回転子鉄心のスロットに挿入され、両端部で短絡環により電気的に接続されています。この構造は、リスのかごに似ていることから「スクイレルケージ」と呼ばれています。導体棒と短絡環はしばしば一体成型されており、シンプルな構造でありながら堅牢性と信頼性を兼ね備えています。

2.4 単相と三相誘導電動機

誘導電動機は電源の相数によって、単相誘導電動機と三相誘導電動機に分類されます：

単相誘導電動機：
- 単相交流電源で駆動
- 主に家庭用機器や小型産業機器に使用
- 自己始動能力がないため、補助巻線や他の始動方式が必要
- 種類：コンデンサ始動型、コンデンサ運転型、分相始動型、シェーディングコイル型など
三相誘導電動機：
- 三相交流電源で駆動
- 産業用途で最も広く使用
- 自己始動能力あり
- 大きなトルクと高効率が特徴

単相誘導電動機の始動方式
単相誘導電動機は単相電源だけでは回転磁界を作れないため、自己始動することができません。そのため、以下のような始動方式が採用されています：

分相始動型：主巻線と補助巻線の間に位相差を持たせて始動時に回転磁界を作ります。
コンデンサ始動型：補助巻線に直列にコンデンサを接続し、始動時のみ使用します。
コンデンサ運転型：始動用と運転用の2つのコンデンサを使用して、始動性能と運転性能の両方を向上させます。
シェーディングコイル型：固定子の極の一部に短絡輪（シェーディングコイル）を設けて磁束の位相差を作ります。

図5: 単相誘導電動機（左）と三相誘導電動機（右）の構造比較

誘導電動機の基本構造のまとめ

誘導電動機は主に固定子（ステータ）と回転子（ロータ）から構成される
固定子は鉄心、巻線、フレームから成り、交流電流により回転磁界を発生させる
回転子は主にかご形とスリップリング形の2種類があり、それぞれ特性が異なる
かご形はシンプルで堅牢、スリップリング形は外部抵抗接続による制御が可能
電源相数により単相と三相に分類され、三相誘導電動機が産業用途で広く使用される
単相誘導電動機は自己始動能力がないため、様々な始動方式が採用されている

3. 誘導電動機の動作原理

誘導電動機の動作は、電磁誘導の原理と回転磁界の概念に基づいています。このセクションでは、誘導電動機がどのように電気エネルギーを機械的エネルギーに変換するかを説明します。

3.1 回転磁界の発生

回転磁界とは、空間内で回転するように見える磁界のことです。三相誘導電動機では、固定子の3つの巻線に120°の位相差を持つ三相交流を供給することで、一定の速度で回転する磁界が発生します。

三相交流が固定子巻線に流れると、各相の電流は時間的に正弦波状に変化します。それに伴い、各相の作る磁界の大きさと方向も変化します。3つの磁界を合成すると、一定の大きさを持ち、空間内を回転する合成磁界（回転磁界）が形成されます。

回転磁界の同期速度は次の式で表されます：

\[n_s = \frac{120f}{p}\]

ここで：

\(n_s\)：同期速度 [r/min]（毎分回転数）
\(f\)：電源周波数 [Hz]
\(p\)：固定子の極数

回転磁界の速度計算例
4極の三相誘導電動機を50Hzの電源で運転する場合の回転磁界の速度は：

\begin{align*} n_s &= \frac{120f}{p} \\ &= \frac{120 \times 50}{4} \\ &= \frac{6000}{4} \\ &= 1500 \, \mathrm{r/min} \end{align*}

したがって、回転磁界は毎分750回転の速度で回転します。日本では、東日本で50Hz、西日本で60Hzの電源周波数が使用されているため、同じ電動機でも地域によって同期速度が異なることがあります。

3.2 電磁誘導と誘導起電力

固定子の作る回転磁界が回転子を横切ると、ファラデーの電磁誘導の法則により、回転子の導体に起電力が誘導されます。

ファラデーの電磁誘導の法則
導体を貫く磁束が変化するとき、その変化を妨げる方向に起電力が誘導されます。誘導起電力の大きさは磁束の時間変化率に比例します：

\[e = -\frac{d\Phi}{dt}\]

ここで、\(e\) は誘導起電力、\(\Phi\) は磁束です。

回転子の導体は閉回路（かご形では短絡環で閉じられている）を形成しているため、誘導起電力によって回転子に電流が流れます。この電流を「誘導電流」または「渦電流」と呼びます。

誘導電流が流れる条件は、回転子の速度が回転磁界の速度（同期速度）と異なる場合のみです。回転子が回転磁界と同じ速度で回転している場合、相対的な磁束の変化がないため、誘導起電力は発生しません。

3.3 トルクの発生メカニズム

回転子に誘導された電流と固定子の作る磁界との相互作用により、回転子に力（トルク）が発生します。これはフレミングの左手の法則で説明できます。

フレミングの左手の法則
導体に電流が流れ、その周りに磁界がある場合、導体には力が働きます。左手の親指、人差し指、中指を互いに直角に伸ばしたとき、人差し指を磁界の方向に、中指を電流の方向に向けると、親指は導体に働く力の方向を示します。

誘導電動機のトルクは次の式で近似的に表すことができます：

\[T \propto \frac{E_2 I_2 \cos \phi_2}{n_s}\]

ここで：

\(T\)：トルク [N・m]
\(E_2\)：回転子に誘導される起電力
\(I_2\)：回転子に流れる電流
\(\cos \phi_2\)：回転子回路の力率
\(n_s\)：同期速度 [r/min]

発生したトルクにより回転子は回転しますが、回転子の速度が回転磁界の速度（同期速度）に近づくほど、誘導起電力と電流は小さくなり、結果としてトルクも減少します。実際の運転状態では、回転子は常に回転磁界より遅い速度で回転しています。

3.4 すべりの概念

すべりとは、回転磁界の速度（同期速度）と回転子の実際の速度の差を、同期速度に対する比率で表したものです。すべりは誘導電動機の動作状態を表す重要なパラメータです。

\[s = \frac{n_s - n}{n_s}\]

ここで：

\(s\)：すべり（0から1の間の値）
\(n_s\)：同期速度 [r/min]
\(n\)：回転子の実際の速度 [r/min]

すべりと動作状態の関係は以下のようになります：

\(s = 0\)：回転子が同期速度で回転（トルクは発生しない）
\(0 < s < 1\)：通常の電動機運転状態
\(s = 1\)：回転子が静止状態（始動時）
\(s > 1\)：制動（ブレーキ）動作
\(s < 0\)：発電機運転

すべりの計算例
同期速度が1500 r/minの誘導電動機が、実際には1440 r/minで回転している場合のすべりは：

\begin{align*} s &= \frac{n_s - n}{n_s} \\ &= \frac{1500 - 1440}{1500} \\ &= \frac{60}{1500} \\ &= 0.04 \text{ または } 4\% \end{align*}

つまり、回転子は同期速度より4%遅れて回転していることになります。一般的な誘導電動機の定格運転時のすべりは2〜5%程度です。

すべりは回転子に誘導される起電力の周波数にも関係します。回転子の誘導起電力の周波数（すべり周波数）は次式で表されます：

\[f_2 = s \times f\]

ここで：

\(f_2\)：回転子の誘導起電力の周波数 [Hz]
\(s\)：すべり
\(f\)：電源周波数 [Hz]

始動時（\(s = 1\)）には回転子の周波数は電源周波数と同じですが、速度が上がるにつれてすべりが小さくなり、回転子周波数も低下します。これは回転子のインピーダンス特性に影響し、電動機の特性を決定する重要な要素となります。

誘導電動機の動作原理のまとめ

固定子の三相巻線に三相交流を流すと回転磁界が発生する
回転磁界の速度（同期速度）は \(n_s = \frac{60f}{p}\) で表される
回転磁界により回転子に起電力が誘導され、回転子回路に電流が流れる
回転子電流と回転磁界の相互作用によりトルクが発生し、回転子が回転する
すべり \(s\) は回転磁界と回転子の相対速度を表し、電動機の動作状態を示す重要なパラメータ
回転子に誘導される電流の周波数はすべり周波数 \(f_2 = s \times f\) で表される

4. 誘導電動機の特性

誘導電動機の性能を理解するためには、その特性を知ることが重要です。このセクションでは、誘導電動機の速度-トルク特性、効率、力率、始動特性について解説します。

4.1 速度-トルク特性

誘導電動機の速度-トルク特性は、回転子の速度とトルクの関係を示す曲線です。この特性は電動機の運転状態を理解する上で最も基本的なものです。

速度-トルク特性曲線の主要な点は以下の通りです：

始動トルク（起動トルク）：回転子が静止状態（\(s = 1\)）から回転を開始する際のトルク
最大トルク（限界トルク）：電動機が発生できる最大のトルク。この点を超えると電動機は失速します
定格トルク：定格出力と定格速度での連続運転が可能なトルク

トルクとすべりの関係は、近似的に次の式で表されます：

\[T \propto \frac{sV_1^2R_2}{R_2^2 + (sX_2)^2}\]

ここで：

\(T\)：トルク
\(s\)：すべり
\(V_1\)：固定子印加電圧
\(R_2\)：回転子抵抗（固定子側に換算）
\(X_2\)：回転子リアクタンス（固定子側に換算、すべり \(s = 1\) での値）

最大トルクとすべりの関係
最大トルクが発生するすべり \(s_m\) は次式で与えられます：

\[s_m = \frac{R_2}{X_2}\]

この式から、回転子抵抗 \(R_2\) を大きくすると最大トルクが発生するすべりが大きくなり、始動特性が向上することがわかります。これがスリップリング形誘導電動機で外部抵抗を使用する理由の一つです。

速度-トルク特性の例
かご形誘導電動機では、始動トルクは定格トルクの1.5〜2倍程度、最大トルクは定格トルクの2〜3倍程度です。一方、スリップリング形誘導電動機で外部抵抗を接続した場合、始動トルクを定格トルクの2.5〜3倍程度まで増加させることができます。

4.2 効率と損失

誘導電動機の効率は、入力電力に対する出力機械パワーの比率で表されます：

\[\eta = \frac{P_o}{P_i} \times 100\%\]

ここで：

\(\eta\)：効率 [%]
\(P_o\)：機械的出力 [W]
\(P_i\)：電気的入力 [W]

誘導電動機の損失は主に以下の5つに分類されます：

固定子銅損：固定子巻線の抵抗による損失 \(P_{s} = 3I_1^2R_1\)
回転子銅損：回転子巻線（または導体棒）の抵抗による損失 \(P_{r} = sP_g\)
鉄損：ヒステリシス損と渦電流損からなる鉄心での損失
機械損：摩擦、風損などの機械的損失
漂遊負荷損：上記以外の追加負荷に依存する損失

回転子銅損は特に重要で、すべり \(s\) に比例します。つまり、すべりが大きいほど回転子での損失が大きくなります。効率を上げるためには、定格運転時のすべりを小さく（通常2〜5%程度）設計します。

効率計算の例
入力電力が5.5 kWで、機械的出力が5.0 kWの誘導電動機の効率は：

\begin{align*} \eta &= \frac{P_o}{P_i} \times 100\% \\ &= \frac{5.0}{5.5} \times 100\% \\ &= 90.9\% \end{align*}

一般的な三相誘導電動機の効率は、大きさにもよりますが、80〜95%程度です。大型の電動機ほど効率が高くなる傾向があります。

4.3 力率

力率は、電気的入力の皮相電力に対する有効電力の比率で、電源の電圧と電流の位相差の余弦（cosφ）として表されます：

\[\text{力率} = \cos\phi = \frac{P}{VI} = \frac{P}{S}\]

ここで：

\(\cos\phi\)：力率
\(P\)：有効電力 [W]
\(V\)：電圧 [V]
\(I\)：電流 [A]
\(S\)：皮相電力 [VA]

誘導電動機は本質的に誘導性負荷であり、力率は通常遅れ（lagging）となります。力率は負荷条件によって変化し、軽負荷時には低く、負荷が増加するにつれて向上します。

一般的な三相誘導電動機の定格負荷時の力率は、大きさにもよりますが、0.75〜0.90程度です。低い力率は以下のような問題を引き起こします：

電源設備の容量が効率的に利用できない
同じ有効電力を得るために大きな電流が必要となり、線路損失が増加する
電圧降下が増加し、系統電圧が不安定になりやすい

力率改善
誘導電動機の力率を改善するためには、コンデンサを並列に接続する方法が一般的です。コンデンサは進み（leading）の無効電力を供給して、誘導電動機の遅れ無効電力を相殺します。これにより、系統から見た力率が改善されます。

4.4 始動特性

誘導電動機の始動時には、回転子が静止状態（\(s = 1\)）にあるため、特有の特性を示します：

始動電流：定格電流の5〜8倍程度の大きな電流が流れる
始動トルク：かご形では定格トルクの1.5〜2倍程度、スリップリング形では外部抵抗により調整可能

始動電流が大きい理由は、始動時には回転子のインピーダンスが低く、また逆起電力が発生していないためです。この大きな始動電流は、電源系統に電圧降下を引き起こしたり、保護装置が動作したりする原因となります。

始動特性を改善するために、以下のような方法が用いられます：

直入れ始動：小型機や電源容量が十分大きい場合に使用
スターデルタ始動：始動時はスター結線、運転時はデルタ結線に切り替える
リアクトル始動：始動時に直列リアクトルを挿入して始動電流を制限
オートトランス始動：始動時に降圧した電圧を印加
外部抵抗始動：スリップリング形電動機で回転子回路に抵抗を挿入
インバータ始動：可変周波数制御により始動電流を制限

スターデルタ始動
スターデルタ始動では、始動時の相電圧がデルタ結線時の \(1/\sqrt{3}\) になるため、相電流は約1/3になります。これにより、始動電流を定格電流の約2〜2.5倍に抑えることができます。しかし、始動トルクも定格トルクの約1/3になるため、軽負荷始動が必要です。

誘導電動機の特性のまとめ

速度-トルク特性は、始動トルク、最大トルク、定格トルクの関係を示す重要な特性
最大トルクが発生するすべりは回転子抵抗とリアクタンスの比 \(s_m = \frac{R_2}{X_2}\) で決まる
効率は入力電力に対する出力機械パワーの比率で、通常80〜95%程度
損失には固定子銅損、回転子銅損、鉄損、機械損、漂遊負荷損がある
力率は定格負荷時で0.75〜0.90程度で、軽負荷時には低下する
始動電流は定格電流の5〜8倍、始動トルクはかご形で定格トルクの1.5〜2倍程度
始動特性の改善にはスターデルタ始動、リアクトル始動、外部抵抗始動などの方法がある

5. 誘導電動機の応用と制御

誘導電動機は、その堅牢な構造と高い信頼性から、様々な産業分野で広く使用されています。このセクションでは、誘導電動機の応用例と制御方法について解説します。

5.1 産業応用

誘導電動機は以下のような多様な用途で使用されています：

製造業：工作機械、コンベヤシステム、圧縮機、ポンプ
建設業：クレーン、リフト、コンクリートミキサー
空調設備：送風機、冷却塔、冷凍機
水処理設備：ポンプ、攪拌機
輸送機器：エレベーター、エスカレーター、電気鉄道
家庭用機器：洗濯機、エアコン、冷蔵庫（主に単相誘導電動機）

ポンプ用途での誘導電動機の例
水処理施設では、大型の三相誘導電動機が遠心ポンプを駆動するために使用されています。このような用途では、高い始動トルクが必要となるため、スリップリング形誘導電動機が選ばれることがあります。また、流量制御のためにインバータ制御を採用し、ポンプの速度を必要に応じて変化させることで、エネルギー効率を向上させています。

誘導電動機の選定には、負荷の特性（必要トルク、速度範囲、運転サイクル）、環境条件（温度、湿度、粉塵、危険区域）、電源条件（電圧、周波数、相数）などを考慮する必要があります。

5.2 始動方式

誘導電動機の主な始動方式とその特徴を以下に示します：

始動方式	始動電流	始動トルク	適用範囲
直入れ始動	定格の5〜8倍	定格の1.5〜2倍	小型機（22kW以下）
スターデルタ始動	直入れの約1/3	直入れの約1/3	中型機（75kWまで）
リアクトル始動	直入れの0.5〜0.8倍	直入れの0.25〜0.64倍	中〜大型機
オートトランス始動	電圧比の二乗に比例	電圧比の二乗に比例	中〜大型機
外部抵抗始動	抵抗値により調整可能	抵抗値により調整可能	スリップリング形のみ
ソフトスタート	制御範囲内で調整可能	電圧の二乗に比例	電子制御装置が必要
インバータ始動	定格程度まで制限可能	必要に応じて調整可能	インバータ装置が必要

始動方式の選定
始動方式の選定には、以下の要素を考慮する必要があります：

電源容量と電圧降下の許容範囲
負荷の種類と始動トルク要件
始動頻度
初期コストと運用コスト
保守性と信頼性

5.3 速度制御法

誘導電動機の速度制御には、以下の方法があります：

極数変換法：固定子巻線の接続を変えて極数を変更し、同期速度 \(n_s = \frac{120f}{p}\) を変える方法
電圧制御法：固定子電圧を変えてトルク曲線を変化させる方法（軽負荷用）
回転子抵抗制御法：スリップリング形で回転子回路の抵抗を調整する方法
周波数制御法：インバータを使用して電源周波数を変化させる方法
カスケード制御法：スリップリング形電動機の回転子電力を回収して利用する方法

極数変換による速度制御の例
ダランダ結線を用いた4極/8極の切り替えが可能な誘導電動機の場合、50Hzの電源で運転すると次のような同期速度が得られます：

4極の場合：\(n_s = \frac{120 \times 50}{4} = 1500 \, \mathrm{r/min}\)
8極の場合：\(n_s = \frac{120 \times 50}{8} = 750 \, \mathrm{r/min}\)

このように、極数を変えることで同期速度を段階的に変更することができます。多段極数変換では、2:1の比率で3段階以上の速度制御も可能です。

各制御法の特徴比較：

制御方法	速度範囲	効率	コスト	適用範囲
極数変換法	段階的（比率2:1）	高い	中程度	段階的速度制御が可能な場合
電圧制御法	狭い（20%程度）	低い	低い	ファン、ポンプなどの軽負荷
回転子抵抗制御法	中程度（30%程度）	低い	中程度	スリップリング形のみ
周波数制御法	広い（0〜100%以上）	高い	高い	広範囲な速度制御が必要な場合
カスケード制御法	中程度（同期速度以下）	中程度	高い	スリップリング形の大型機

5.4 インバータ制御

インバータ制御は、現代の誘導電動機制御において最も重要な方法です。インバータは交流を一度直流に変換し、再び所望の周波数と電圧の交流に変換する装置です。

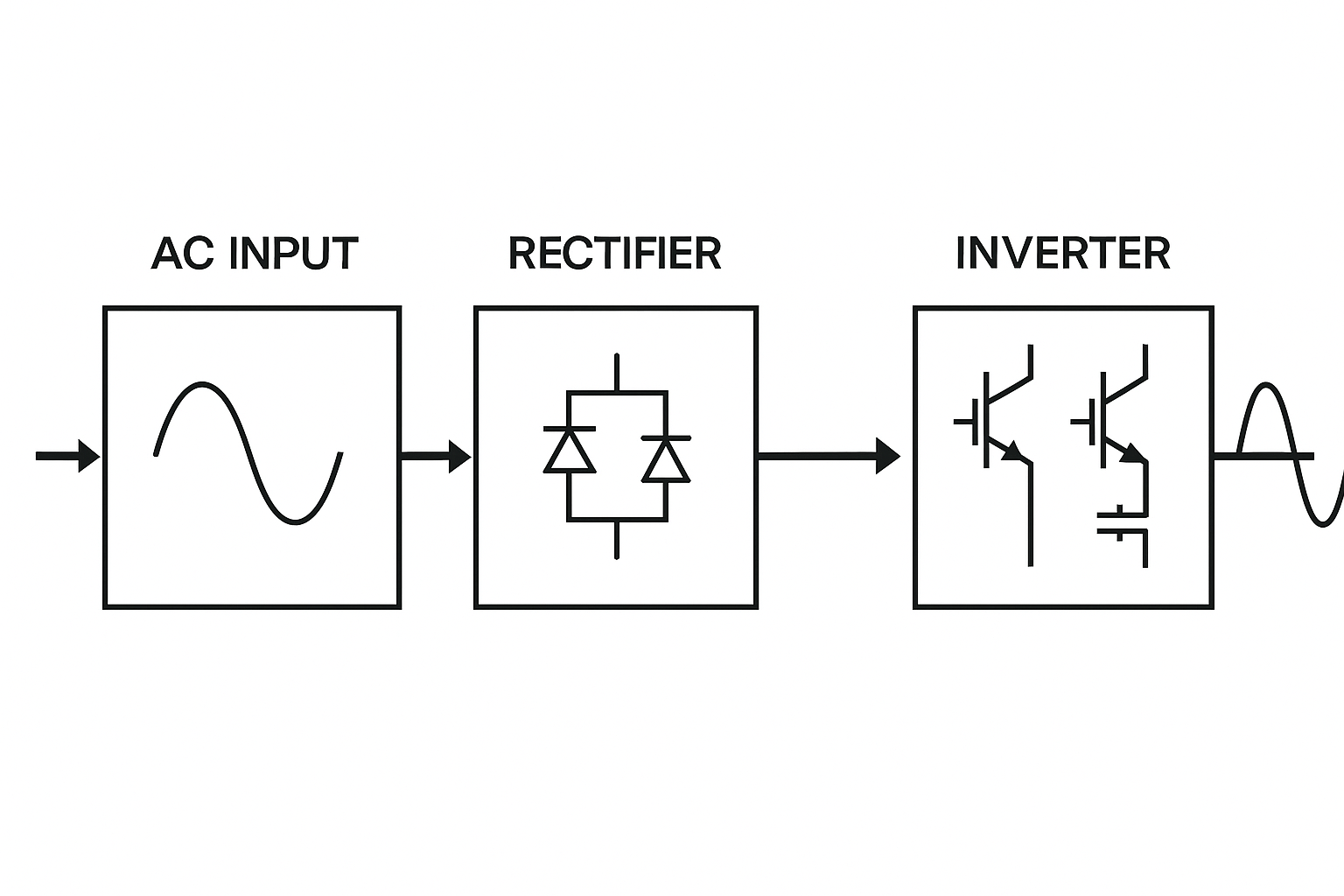
図6: インバータの基本構成（整流器、DC部、インバータ部）

インバータ制御には主に以下の方式があります：

V/f一定制御：周波数と電圧の比を一定に保ち、基本的なトルク特性を維持
磁束ベクトル制御：トルク電流と励磁電流を分離制御し、高精度なトルク制御を実現
直接トルク制御：トルクと磁束を直接制御し、高速応答性を実現

V/f一定制御の原理
誘導電動機の発生トルクは固定子磁束に比例し、固定子磁束は印加電圧を周波数で割った値（V/f）に比例します。したがって、周波数を変化させるときに電圧も比例して変化させれば（V/f一定）、全速度範囲でほぼ一定のトルク特性が得られます。

\[V \propto f \times \Phi\]

ここで、\(V\) は印加電圧、\(f\) は周波数、\(\Phi\) は磁束です。

インバータ制御のメリット：

広範囲な速度制御が可能（0〜120%程度）
高効率な運転が可能（特に可変トルク負荷）
始動電流の制限が可能
加速・減速時間の制御が可能
回生ブレーキ機能を利用できる
様々な保護機能を組み込める

インバータによるエネルギー節約の例
ポンプやファンなどの可変トルク負荷では、流量制御をバルブやダンパーで行う代わりにインバータで回転速度を制御すると、大幅なエネルギー節約になります。ポンプの消費電力は回転速度の3乗に比例するため、流量を50%に減らす場合、回転速度を50%にすれば消費電力は約12.5%（0.5³）に減少します。これに対し、バルブで流量を絞る方法では、消費電力はあまり減少しません。

インバータ制御の課題：

高調波の発生と対策
電動機絶縁への過電圧ストレス
軸電流とベアリング損傷
電磁ノイズの発生
初期コストが比較的高い

誘導電動機の応用と制御のまとめ

誘導電動機は製造業、建設業、空調設備、水処理設備など幅広い産業で利用されている
始動方式には直入れ、スターデルタ、リアクトル、オートトランス、外部抵抗、ソフトスタート、インバータ始動などがある
速度制御法には極数変換法、電圧制御法、回転子抵抗制御法、周波数制御法、カスケード制御法がある
インバータ制御はV/f一定制御、磁束ベクトル制御、直接トルク制御などの方式があり、広範囲な速度制御と省エネルギー運転が可能
インバータ制御は高調波、過電圧、軸電流、電磁ノイズなどの課題にも対処する必要がある

6. 演習問題

6.1 基本計算問題

問題1：同期速度とすべりの計算

6極の三相誘導電動機が60Hzの電源で運転され、回転速度が1140 r/minのとき、(a) 同期速度と (b) すべりを求めよ。

解答：

(a) 同期速度の計算：

同期速度は次の式で求められます：

\[n_s = \frac{120f}{p}\]

ここで：

\(n_s\)：同期速度 [r/min]
\(f\)：電源周波数 = 60 Hz
\(p\)：極数 = 6

これらの値を式に代入すると：

\begin{align*} n_s &= \frac{120 \times 60}{6} \\[10pt] &= \frac{7200}{6} \\[10pt] &= 1200 \, \mathrm{r/min} \end{align*}

(b) すべりの計算：

すべりは次の式で求められます：

\[s = \frac{n_s - n}{n_s}\]

ここで：

\(s\)：すべり
\(n_s\)：同期速度 = 1200 r/min
\(n\)：実際の回転速度 = 1140 r/min

これらの値を式に代入すると：

\begin{align*} s &= \frac{1200 - 1140}{1200} \\[10pt] &= \frac{60}{1200} \\[10pt] &= 0.05 \text{ または } 5\% \end{align*}

したがって、同期速度は1200 r/min、すべりは0.05（5%）です。このすべりの値は、定格負荷時の典型的な範囲（2〜5%）の上限に相当します。

問題2：誘導電動機の出力と効率

三相誘導電動機が200V、50Hz、25Aで運転されており、力率は0.85、効率は0.88である。この電動機の機械的出力を求めよ。

解答：

三相誘導電動機の入力電力は次の式で求められます：

\[P_i = \sqrt{3} \times V \times I \times \cos\phi\]

ここで：

\(P_i\)：入力電力 [W]
\(V\)：線間電圧 = 200 V
\(I\)：線電流 = 25 A
\(\cos\phi\)：力率 = 0.85

これらの値を式に代入すると：

\begin{align*} P_i &= \sqrt{3} \times 200 \times 25 \times 0.85 \\[10pt] &= 1.732 \times 200 \times 25 \times 0.85 \\[10pt] &= 7361 \, \mathrm{W} \\[10pt] &= 7.361 \, \mathrm{kW} \end{align*}

機械的出力は、入力電力と効率の積で求められます：

\[P_o = P_i \times \eta\]

ここで：

\(P_o\)：機械的出力 [W]
\(P_i\)：入力電力 = 7.361 kW
\(\eta\)：効率 = 0.88

これらの値を式に代入すると：

\begin{align*} P_o &= 7.361 \times 0.88 \\ &= 6.478 \, \mathrm{kW} \end{align*}

したがって、電動機の機械的出力は約6.48 kWです。

問題3：回転子周波数の計算

50Hzの電源で運転される4極の三相誘導電動機の回転速度が1425 r/minである。回転子に誘導される電流の周波数を求めよ。

解答：

まず、同期速度を計算します：

\[n_s = \frac{120f}{p}\]

ここで：

\(n_s\)：同期速度 [r/min]
\(f\)：電源周波数 = 50 Hz
\(p\)：極数 = 4

これらの値を式に代入すると：

\begin{align*} n_s &= \frac{120 \times 50}{4} \\[10pt] &= \frac{6000}{4} \\[10pt] &= 1500 \, \mathrm{r/min} \end{align*}

次に、すべりを計算します：

\[s = \frac{n_s - n}{n_s}\]

ここで：

\(s\)：すべり
\(n_s\)：同期速度 = 1500 r/min
\(n\)：実際の回転速度 = 1425 r/min

これらの値を式に代入すると：

\begin{align*} s &= \frac{1500 - 1425}{1500} \\[10pt] &= \frac{75}{1500} \\[10pt] &= 0.05 \text{ または } 5\% \end{align*}

回転子周波数（すべり周波数）は、すべりと電源周波数の積で求められます：

\[f_2 = s \times f\]

ここで：

\(f_2\)：回転子周波数 [Hz]
\(s\)：すべり = 0.05
\(f\)：電源周波数 = 50 Hz

これらの値を式に代入すると：

\begin{align*} f_2 &= 0.05 \times 50 \\ &= 2.5 \, \mathrm{Hz} \end{align*}

したがって、回転子に誘導される電流の周波数は2.5 Hzです。これは、回転子がすべり速度（同期速度と回転子速度の差）で回転磁界内を動くため、回転子から見た磁界の周波数が低下することを示しています。

6.2 過去問題

問題4：第三種電気主任技術者試験過去問（類似問題）

6極の三相誘導電動機を60Hzの電源に接続して運転したとき、回転子の速度が1164 r/minであった。この状態における回転磁界の速度とすべりはそれぞれいくらか。

解答：

(1) 回転磁界の速度（同期速度）の計算：

\[n_s = \frac{120f}{p}\]

ここで：

\(n_s\)：同期速度 [r/min]
\(f\)：電源周波数 = 60 Hz
\(p\)：極数 = 6

これらの値を式に代入すると：

\begin{align*} n_s &= \frac{120 \times 60}{6} \\[10pt] &= \frac{7200}{6} \\[10pt] &= 1200 \, \mathrm{r/min} \end{align*}

(2) すべりの計算：

\[s = \frac{n_s - n}{n_s}\]

ここで：

\(s\)：すべり
\(n_s\)：同期速度 = 1200 r/min
\(n\)：実際の回転速度 = 1164 r/min

これらの値を式に代入すると：

\begin{align*} s &= \frac{1200 - 1164}{1200} \\[10pt] &= \frac{36}{1200} \\[10pt] &= 0.03 \text{ または } 3\% \end{align*}

したがって、回転磁界の速度は1200 r/min、すべりは0.03（3%）です。

問題5：第三種電気主任技術者試験過去問（類似問題）

定格出力5.5kWの三相誘導電動機があり、定格電圧200V、定格効率87%、定格力率0.83で運転されている。この電動機の全負荷時の線電流はいくらか。

解答：

三相誘導電動機の入力電力と出力の関係は次のようになります：

\[P_i = \frac{P_o}{\eta}\]

ここで：

\(P_i\)：入力電力 [W]
\(P_o\)：出力電力 = 5.5 kW = 5500 W
\(\eta\)：効率 = 0.87

これらの値を式に代入すると：

\begin{align*} P_i &= \frac{5500}{0.87} \\[10pt] &= 6321.8 \, \mathrm{W} \end{align*}

三相交流回路では、入力電力は次の式で表されます：

\[P_i = \sqrt{3} \times V \times I \times \cos\phi\]

この式を電流 \(I\) について解きます：

\[I = \frac{P_i}{\sqrt{3} \times V \times \cos\phi}\]

ここで：

\(I\)：線電流 [A]
\(P_i\)：入力電力 = 6321.8 W
\(V\)：線間電圧 = 200 V
\(\cos\phi\)：力率 = 0.83

これらの値を式に代入すると：

\begin{align*} I &= \frac{6321.8}{\sqrt{3} \times 200 \times 0.83} \\[10pt] &= \frac{6321.8}{1.732 \times 200 \times 0.83} \\[10pt] &= \frac{6321.8}{287.5} \\[10pt] &= 21.99 \, \mathrm{A} \\[10pt] &\approx 22 \, \mathrm{A} \end{align*}

したがって、全負荷時の線電流は約22 Aです。

演習問題のポイント

同期速度の計算：\(n_s = \frac{120f}{p}\)を正確に使用すること
すべりの計算：\(s = \frac{n_s - n}{n_s}\)を正確に使用すること
回転子周波数（すべり周波数）の計算：\(f_2 = s \times f\)を理解すること
三相電力の計算：\(P_i = \sqrt{3} \times V \times I \times \cos\phi\)を正確に使用すること
効率と入出力の関係：\(P_o = P_i \times \eta\) または \(P_i = \frac{P_o}{\eta}\)を理解すること
単位の一貫性に注意すること（特にkWとWの変換）

まとめ

本ページでは、第三種電気主任技術者試験の重要分野である「誘導電動機」について学習しました。誘導電動機の基本構造から動作原理、特性、応用と制御まで、幅広く解説しています。誘導電動機は産業界で最も広く使用されている電動機であり、その特性を理解することは電気技術者にとって非常に重要です。

三相誘導電動機シミュレーション｜回転原理やすべりを視覚で理解

本ページの内容をしっかりと理解し、演習問題を繰り返し解くことで、試験での得点力向上につながります。また、実務においても誘導電動機の選定や運用、トラブルシューティングに役立つ知識となるでしょう。

学習のポイント
誘導電動機の学習で特に重要な点は以下の通りです：

回転磁界の発生原理と同期速度の計算方法を理解する
すべりの概念とその物理的意味を把握する
速度-トルク特性曲線の形状と各動作点の意味を理解する
固定子と回転子の損失メカニズムと効率への影響を理解する
始動方式の種類とそれぞれの特徴を比較できる
速度制御方法、特にインバータ制御の原理と特性を理解する

次回の学習では、「同期電動機」について解説します。同期電動機は誘導電動機と並ぶ重要な交流電動機であり、その特性と応用の違いを理解することで、電動機に関する知識がさらに深まります。

【第三種電気主任技術者試験】誘導電動機の完全解説 - 構造から特性・制御まで

目次

1. イントロダクション

2. 誘導電動機の基本構造

2.1 固定子（ステータ）の構造

2.2 回転子（ロータ）の構造

2.3 かご形とスリップリング形

2.4 単相と三相誘導電動機

3. 誘導電動機の動作原理

3.1 回転磁界の発生

3.2 電磁誘導と誘導起電力

3.3 トルクの発生メカニズム

3.4 すべりの概念

4. 誘導電動機の特性

4.1 速度-トルク特性

4.2 効率と損失

4.3 力率

4.4 始動特性

5. 誘導電動機の応用と制御

5.1 産業応用

5.2 始動方式

5.3 速度制御法

5.4 インバータ制御

6. 演習問題

6.1 基本計算問題

6.2 過去問題

まとめ