ようこそ！このページでは、電気系資格試験に出てくる数学の基礎をわかりやすく解説していきます！特に三平方の定理は試験でよく出るので、しっかり押さえておきましょう！
三平方の定理の基本から応用まで、電気系資格試験でよく出る計算方法を詳しく解説します。
三平方の定理（さんへいほうのていり）とは、直角三角形において「斜辺の長さの二乗は、他の二辺の長さの二乗の和に等しい」という定理です。これはピタゴラスの定理とも呼ばれています。
三平方の定理の公式は以下のようになります：
三平方の定理は様々な場面で活用できます。まずは基本的な使い方を見てみましょう。
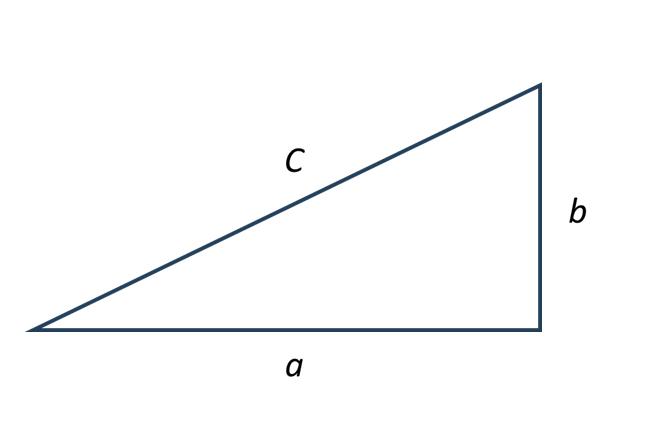
直角三角形の3つの辺の長さを以下のように表します：
\(a, b\)：直角をはさむ二辺（短辺）の長さ
\(c\)：斜辺（最も長い辺）の長さ
この公式を使うことで、2つの辺の長さがわかれば残りの1つの辺の長さも計算できます。
三平方の定理を使って、直角三角形の辺の長さを求める方法を見ていきましょう。
直角をはさむ一辺の長さを求める場合：
三平方の定理は、実生活の様々な問題解決に役立ちます。
電気工学では、立体的な距離や高さを計算する場面が多く、三平方の定理は非常に有用です。
辺の比が3:4:5の三角形は、常に直角三角形になります。これは計算を素早く行うために覚えておくと便利です。
正方形の対角線の長さは、一辺の長さの\(\sqrt{2}\)倍になります。電気工学の計算でよく出てくるパターンです。
30-60-90度の三角形の辺の比率：
この比率を覚えておくと、様々な計算が簡単になります。
直角三角形の2辺の長さが\(a=6\)cm、
\(b=8\)cmのとき、斜辺の長さ\(c\)を求めよ。
三平方の定理を使って計算します：
直角三角形の斜辺が\(c=13\)cm、直角を
はさむ一辺が\(a=5\)cmのとき、
もう一辺の長さ\(b\)を求めよ。
三平方の定理から、\(a^2 + b^2 = c^2\)なので、\(b\)について解きます：
電柱の頂点から地面に12mの影が
できています。太陽の高度が
30度のとき、電柱の高さを求めよ。
影の長さと電柱の高さで直角三角形ができます：
一辺の長さが8cmの正方形の
対角線の長さを求めよ。
正方形の対角線は、三平方の定理を使って計算できます：
高さ4cm、底面が一辺3cmの
正方形である直方体の対角線の
長さを求めよ。
立体の対角線は、三平方の定理を2回使って求めます：
これらの例題を通じて、三平方の定理の使い方が身につくと思います。さらに練習を重ねることで、もっと複雑な問題も解けるようになります！電気系の試験でこの辺りの問題がバッチリ解けるようになったら、合格に一歩近づきます！頑張りましょう！
ほな、学んだことを使って実際に解いてみよか！答えは隠してあるから、自分で計算してから確認してな。答えを見るには「答えを表示」ボタンをクリックするか、答えの部分をタッチしてみてな！
次の直角三角形の斜辺の長さを求めよ：
直角をはさむ二辺の長さが
\(a=5\)cmと\(b=12\)cm
次の直角三角形の一辺の長さを求めよ：
斜辺の長さが\(c=10\)cm、
直角をはさむ一辺が\(a=6\)cm
次の問題を解け：
壁から9m離れたところから、
壁に立てかけた梯子が壁の12mの高さに届きます。この梯子の
長さを求めよ。
次の問題を解け：
縦が7cm、横が24cmの
長方形の対角線の長さ
を求めよ。
次の問題を解け：
一辺の長さが5cmの
立方体の対角線の長さ
を求めよ。
練習問題はどうやった？正解できたかな？