【法規】令和6年(下期) 問12|三相電路の接地設計と漏洩電流に関する計算問題
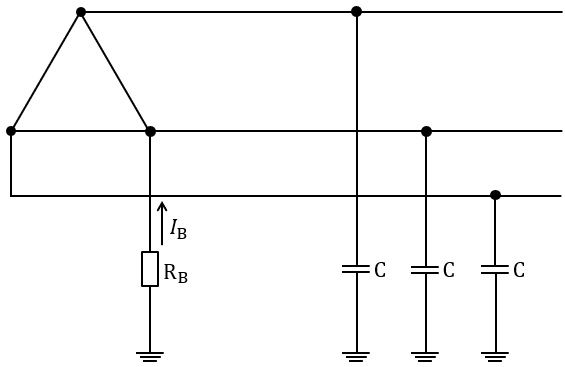
図は三相 \( 3 \) 線式高圧電路に変圧器で結合された変圧器低圧側電路を示したものである。低圧側電路の一端子には \( \mathrm{B} \) 種接地工事が施されている。この電路の一相当たりの対地静電容量を \( \mathrm{C} \) とし、接地抵抗を \( \mathrm{R}_{\mathrm{B}} \) とする。
低圧側電路の線間電圧 \( 200 \) [V]、周波数 \( 50 \) [Hz]、対地静電容量 \( \mathrm{C} \) は \( 0.1 \) [μF] として、次の (a) 及び (b) の問に答えよ。
ただし、
(ア) 変圧器の高圧電路の \( 1 \) 線地絡電流は \( 5 \) [A] とする。
(イ) 高圧側電路と低圧側電路との混触時に低圧電路の対地電圧が \( 150 \) [V] を超えた場合は \( 1.3 \) 秒で自動的に高圧電路を遮断する装置が設けられているものとする。
(a) 変圧器に施された、接地抵抗 \( \mathrm{R}_{\mathrm{B}} \) の抵抗値について「電気設備技術基準の解釈」で許容されている上限の抵抗値 [Ω] として、最も近いものを次の (1)~(5) のうちから一つ選べ。
(b) 接地抵抗 \( \mathrm{R}_{\mathrm{B}} \) の抵抗値を \( 10 \) [Ω] としたときに、\( \mathrm{R}_{\mathrm{B}} \) に常時流れる電流 \( I_{\mathrm{B}} \) の値 [mA] として、最も近いものを次の (1)~(5) のうちから一つ選べ。
ただし,記載以外のインピーダンスは無視するものとする。
合格への方程式
接地工事の基本知識と種類別特徴
なぜ接地工事が必要なの?
接地工事は電気設備の安全を守る超重要な工事です。地絡事故(電気が地面に漏れる事故)が起きたとき、人体への感電を防いだり、機器の破損を防いだりする役割があります。まさに「電気の逃げ道」を作ってあげる工事なんです!
■ 4種類の接地工事を覚えよう
電気設備技術基準では、A種、B種、C種、D種の4種類の接地工事が定められています。それぞれの特徴をしっかり理解しましょう。
| 接地種別 | 主な用途 | 接地抵抗値 | 覚え方のコツ |
|---|---|---|---|
| A種接地 | 高圧・特別高圧機器の外箱 (避雷器など) |
10Ω以下 | 「A(エース)級の重要機器」 →最も厳しい10Ω |
| B種接地 | 高圧側と低圧側の混触防止 (変圧器の低圧側中性点) |
計算式で決定 (後述) |
「B(ビー)=変圧器」 →計算が必要 |
| C種接地 | 300V超の低圧機器の外箱 (400V動力機器など) |
10Ω以下 (条件付き500Ω) |
「C=300V超」 →Cの文字が3に似てる |
| D種接地 | 300V以下の低圧機器の外箱 (100V/200V機器) |
100Ω以下 (条件付き500Ω) |
「D=電灯(Dento)」 →一般家庭用 |
条件付き500Ωって何?
C種とD種では、「0.5秒以内に自動遮断する装置」があれば、接地抵抗を500Ωまで緩和できます。これは、事故が起きてもすぐに電源を切るから、そこまで厳しくしなくてもOKという考え方です。
■ B種接地工事の特殊性
B種接地工事だけが「計算で決まる」という特殊な接地工事です。その理由を理解しましょう。
なぜB種だけ計算式なの?
B種接地は「高圧と低圧の混触事故」を想定しています。高圧側の地絡電流の大きさによって危険度が変わるので、その電流値に応じて接地抵抗を決める必要があるんです。
• 地絡電流が大きい → 危険 → 接地抵抗を小さく
• 地絡電流が小さい → 比較的安全 → 接地抵抗は大きくてもOK
■ 混触事故とは?
変圧器の高圧側巻線と低圧側巻線が何らかの原因で接触してしまう事故です。
混触事故の危険性
通常200Vの低圧側に、6600Vなどの高圧が侵入してきます!
• 低圧機器が破損
• 人体への重大な感電事故
• 火災の発生
これを防ぐのがB種接地の役割です。
■ 変圧器の結線とB種接地
この問題では「三相3線式」の低圧側電路にB種接地が施されています。
| 結線方式 | B種接地の位置 | 特徴 |
|---|---|---|
| 単相3線式 (100V/200V) |
中性線 | 一般家庭で使用 中性線は常に接地電位 |
| 三相3線式 (200V) |
1端子 (S相が多い) |
小規模動力で使用 接地した相は対地電圧0V |
| 三相4線式 (200V/400V) |
中性点 | 大規模施設で使用 中性点接地で安定 |
■ 電気設備技術基準の解釈 第17条
試験では第17条の内容を正確に覚えることが重要です。特にB種接地の17-1表は頻出です!
17-1表(B種接地工事の接地抵抗値)
| 変圧器の種類 | 接地抵抗値の計算式 |
|---|---|
| 高圧側の1線地絡電流が 1秒以内に遮断される場合 |
\[ R_B \leq \frac{600}{I_g} \quad [\Omega] \] |
| 高圧側の1線地絡電流が 1~2秒以内に遮断される場合 |
\[ R_B \leq \frac{300}{I_g} \quad [\Omega] \] |
| 上記以外 (2秒超または遮断装置なし) |
\[ R_B \leq \frac{150}{I_g} \quad [\Omega] \] |
ただし、I_g:高圧側の1線地絡電流 [A]
覚え方のコツ
「600 → 300 → 150」と半分ずつになっていきます。
遮断が遅いほど危険なので、接地抵抗を小さくする必要があるんです。
B種接地抵抗値の計算方法
B種接地抵抗の決め方
B種接地抵抗は「高圧側の地絡電流」と「遮断時間」の2つの要素で決まります。この問題では、遮断時間が1.3秒なので「1~2秒以内」の条件を使います。
■ 問題の条件を整理しよう
まず、問題文から必要な情報を抜き出します:
| 項目 | 与えられた値 | 使用する理由 |
|---|---|---|
| 高圧側1線地絡電流 | 5 A | B種接地抵抗の計算に必要 |
| 遮断時間 | 1.3秒 | 計算式を選ぶため |
| 遮断条件 | 対地電圧150V超 | 遮断装置の動作条件 |
| 線間電圧 | 200V | (b)の計算で使用 |
| 周波数 | 50Hz | (b)の計算で使用 |
| 対地静電容量 | 0.1μF/相 | (b)の計算で使用 |
■ 遮断時間による計算式の選択
Step 1: 遮断時間を確認
問題文:「1.3秒で自動的に高圧電路を遮断」
→ 1秒 < 1.3秒 ≤ 2秒
→ 「1~2秒以内」の条件に該当!
Step 2: 適用する計算式
\[ R_B \leq \frac{300}{I_g} \quad [\Omega] \]■ B種接地抵抗値の計算
計算の実行
\[ \begin{aligned} R_B &\leq \frac{300}{I_g} \\[10pt] &= \frac{300}{5} \\[10pt] &= 60 \quad [\Omega] \end{aligned} \]したがって、B種接地抵抗の上限値は 60Ω となります。
■ なぜこの式で安全が保たれるの?
混触事故時の対地電圧上昇を理解しましょう:
対地電圧上昇のメカニズム
混触事故時、高圧側の地絡電流 I_g がB種接地抵抗 R_B を流れます。
このとき、低圧側の対地電圧上昇 V は:
例:I_g = 5A、R_B = 60Ω のとき
V = 5 × 60 = 300V(これが上限値)
■ 計算式の数値(600, 300, 150)の意味
| 計算式の分子 | 許容電圧上昇 | 遮断時間 | 安全の考え方 |
|---|---|---|---|
| 600 | 600V | 1秒以内 | 短時間なら600Vまで許容 |
| 300 | 300V | 1~2秒 | やや長いので300Vに制限 |
| 150 | 150V | 2秒超 | 長時間なので150Vに制限 |
試験での注意点
• 遮断時間の判定を間違えないこと(1.3秒は「1~2秒」の範囲)
• 計算式の分子(300)を正確に覚える
• 単位はΩ(オーム)であることを確認
• 「以下」なので、60Ωちょうども許容される
■ 実務での考慮事項
実際の設計では、以下の点も考慮します:
余裕を持った設計
• 計算値の70~80%程度で設計することが多い
• 例:上限60Ω → 実際は40~50Ω程度で施工
• 接地抵抗は経年変化で増加する可能性がある
• 定期的な測定と管理が重要
■ よくある間違いパターン
| 間違いの種類 | 誤答例 | 正しい考え方 |
|---|---|---|
| 遮断時間の判定ミス | 1.3秒を「1秒以内」と判定 → 600/5 = 120Ω |
1.3秒は「1~2秒」の範囲 → 300/5 = 60Ω |
| 計算式の選択ミス | 最も安全側の150を使用 → 150/5 = 30Ω |
条件に合った300を使用 → 300/5 = 60Ω |
| A種接地と混同 | A種の10Ωと回答 | B種は計算で決まる → 60Ω |
対地静電容量と漏れ電流の理解
対地静電容量って何?
電線と大地の間にはわずかながらコンデンサ(静電容量)が存在します。これが原因で、正常時でも微小な電流が大地に流れています。この電流を「充電電流」や「容量性漏れ電流」と呼びます。
■ 対地静電容量が生じる理由
電線と大地の関係を、平行平板コンデンサとして考えることができます:
コンデンサの構造との類似
• 上側の極板 = 電線(導体)
• 絶縁体 = 空気や絶縁物
• 下側の極板 = 大地(導体)
この構造により、必然的に静電容量が発生します。
■ 三相回路の対地静電容量
三相3線式回路では、各相がそれぞれ対地静電容量を持ちます:
| 相 | 対地静電容量 | 対地電圧 | 備考 |
|---|---|---|---|
| R相 | C = 0.1μF | 電圧あり | 充電電流が流れる |
| S相(接地) | C = 0.1μF | 0V | 接地されているので電圧なし |
| T相 | C = 0.1μF | 電圧あり | 充電電流が流れる |
■ 容量性リアクタンスの計算
コンデンサのインピーダンス(容量性リアクタンス)は次の式で計算します:
\[ X_C = \frac{1}{2\pi f C} \quad [\Omega] \]1相分のリアクタンス計算
C = 0.1μF = 0.1 × 10⁻⁶ F、f = 50Hz のとき:
\[ \begin{aligned} X_C &= \frac{1}{2\pi \times 50 \times 0.1 \times 10^{-6}} \\[10pt] &= \frac{1}{31.4 \times 10^{-6}} \\[10pt] &≒ 31,831 \quad [\Omega] \end{aligned} \]■ 並列接続時の合成リアクタンス
この問題では、3つの対地静電容量が並列に接続されています:
並列接続の考え方
• S相は接地されているので、電圧源として働かない
• R相とT相の対地静電容量が実質的に並列
• さらにS相の静電容量も並列に加わる
3つの静電容量の並列合成
容量が並列の場合、合成容量は単純に足し算:
\[ C_{合成} = C + C + C = 3C = 3 \times 0.1 = 0.3 \quad [\mu F] \]合成リアクタンスは:
\[ \begin{aligned} X_{合成} &= \frac{1}{2\pi f \times 3C} \\[10pt] &= \frac{X_C}{3} \\[10pt] &= \frac{31,831}{3} \\[10pt] &≒ 10,610 \quad [\Omega] \end{aligned} \]■ 対地電圧の考え方
三相3線式でS相を接地した場合の対地電圧:
| 測定点 | 対地電圧 | 計算方法 |
|---|---|---|
| S相-大地間 | 0V | 接地されているため |
| R相-大地間 | 200V | R-S間の線間電圧 |
| T相-大地間 | 200V | T-S間の線間電圧 |
| 中性点(仮想) | 115.5V | 200/√3 ≒ 115.5V |
■ 充電電流の影響
対地静電容量による充電電流は、以下の問題を引き起こす可能性があります:
充電電流による問題
• 漏電遮断器の不要動作
• 接地抵抗測定の誤差
• 感電事故の危険性増加
• 絶縁抵抗測定への影響
■ 実際の数値感覚
対地静電容量の目安
• ケーブル:0.1~0.5 μF/km
• 架空線:0.005~0.01 μF/km
• 問題の0.1μF/相は、短距離ケーブルの値として妥当
■ 計算を簡単にするコツ
| 計算のポイント | 覚えておくと便利な値 |
|---|---|
| 2π ≒ 6.28 | 概算では 6 として計算してもOK |
| 50Hz での 2πf | 2π × 50 = 314 ≒ 300 |
| 60Hz での 2πf | 2π × 60 = 377 ≒ 380 |
| √3 ≒ 1.732 | 200/√3 ≒ 115V として計算 |
テブナンの定理による電流計算
テブナンの定理とは?
複雑な回路を「電圧源+内部抵抗」の簡単な等価回路に置き換える超便利な定理です。これを使えば、特定の素子に流れる電流を簡単に計算できるようになります!
■ テブナンの定理の手順
テブナンの定理を使う手順は3ステップです:
3つのステップ
Step 1:注目する素子を取り外して、開放電圧 V₀ を求める
Step 2:電圧源を短絡して、内部インピーダンス Z₀ を求める
Step 3:等価回路を作って、電流を計算する
■ Step 1:開放電圧の計算
B種接地抵抗 R_B を取り外したときの端子電圧を求めます。
開放電圧 V₀ の導出
三相3線式でS相が接地されている場合:
• S相は接地されているので電位 = 0V
• 仮想中性点の対地電圧 = 線間電圧/√3
■ なぜ 200/√3 になるの?
| 結線方式 | 線間電圧 | 相電圧 | 関係式 |
|---|---|---|---|
| Y結線 | V_L | V_P | V_L = √3 × V_P |
| Δ結線 | V_L | V_P | V_L = V_P |
| この問題(Y相当) | 200V | 115.5V | 200 = √3 × 115.5 |
■ Step 2:内部インピーダンスの計算
電圧源を短絡して、R_B から見た等価インピーダンスを求めます。
等価リアクタンス X₀ の計算
電圧源を短絡すると、3つの対地静電容量が並列接続になります:
\[ \begin{aligned} X_0 &= \frac{1}{2\pi f \times 3C} \\[10pt] &= \frac{1}{2 \times 3.14 \times 50 \times 3 \times 0.1 \times 10^{-6}} \\[10pt] &= \frac{1}{314 \times 3 \times 0.1 \times 10^{-6}} \\[10pt] &= \frac{1}{94.2 \times 10^{-6}} \\[10pt] &≒ 10,610 \quad [\Omega] \end{aligned} \]■ Step 3:テブナンの等価回路
求めた V₀ と X₀ を使って等価回路を作ります:
等価回路の構成
• 電圧源:V₀ = 115.5V
• 内部リアクタンス:X₀ = 10,610Ω(容量性)
• 外部抵抗:R_B = 10Ω
これらが直列接続された回路になります。
■ 接地抵抗に流れる電流の計算
抵抗とリアクタンスが直列なので、インピーダンスの合成が必要です:
合成インピーダンスと電流計算
\[ \begin{aligned} Z_{合成} &= \sqrt{R_B^2 + X_0^2} \\[10pt] &= \sqrt{10^2 + 10610^2} \\[10pt] &= \sqrt{100 + 112,572,100} \\[10pt] &= \sqrt{112,572,200} \\[10pt] &≒ 10,610 \quad [\Omega] \end{aligned} \]※ X₀ >> R_B なので、実質的に X₀ とほぼ同じ値になります。
電流 I_B の計算:
\[ \begin{aligned} I_B &= \frac{V_0}{Z_{合成}} \\[10pt] &= \frac{115.5}{10,610} \\[10pt] &≒ 0.0109 \quad [A] \\[10pt] &≒ 11 \quad [mA] \end{aligned} \]■ 計算を簡単にする近似
R_B << X₀ の場合(この問題のように10Ω vs 10,610Ω):
実用的な近似計算
\[ Z_{合成} ≒ X_0 \quad \text{(誤差1%未満)} \]これにより、計算が大幅に簡単になります:
\[ I_B ≒ \frac{V_0}{X_0} = \frac{115.5}{10,610} ≒ 11 \text{ mA} \]■ この電流の意味
| 電流の性質 | 説明 | 影響 |
|---|---|---|
| 常時流れる | 正常時でも流れ続ける | 漏電遮断器の設定に注意 |
| 容量性電流 | 電圧より90°位相が進む | 力率への影響は小さい |
| 周波数依存 | 周波数が高いほど増加 | 高調波で問題になることも |
■ テブナンの定理の応用例
他の問題への応用
• ブリッジ回路の平衡条件
• 最大電力供給の条件(マッチング)
• 故障計算での電流分布
• 系統連系時の循環電流計算
■ 試験でのポイント
確実に得点するために
• 開放電圧は「線間電圧/√3」を確実に覚える
• 並列静電容量は「容量が3倍 → リアクタンスは1/3」
• R << X なら、Z ≒ X の近似が使える
• 最終的な単位(mA)への変換を忘れない
🔍 ワンポイントアドバイス:B種接地工事の問題は電験三種の頻出問題です。特に「遮断時間による係数(600/300/150)の使い分け」は確実に覚えましょう。(a)の接地抵抗計算は基本問題なので絶対に落とせません。(b)のテブナンの定理は少し難しいですが、「開放電圧 = 線間電圧/√3」と「3つの容量並列 = リアクタンス1/3」を押さえれば解けます。対地静電容量による電流は「常時流れる微小電流」という点も重要です!
今日は接地工事の問題やな!電気設備で一番大事な安全対策の話や。B種接地工事って聞いたことある?これ、変圧器の低圧側に施す接地のことやねん。まず問題の回路図をイメージして、どんな状況か整理してみよか。
はい、問題文から次の状況を整理します:
【回路構成】
・三相3線式の高圧電路があります
・変圧器で低圧側(200V)に降圧しています
・低圧側の一端子にB種接地工事が施されています
【与えられた条件】
・線間電圧:\( V = 200 \, \mathrm{[V]} \)
・周波数:\( f = 50 \, \mathrm{[Hz]} \)
・対地静電容量:\( C = 0.1 \, \mathrm{[\mu F]} \)(各相)
・高圧側1線地絡電流:\( I_g = 5 \, \mathrm{[A]} \)
・保護装置:対地電圧150V超過で1.3秒以内に遮断
この接地は、高圧側と低圧側が混触した時の安全確保のために必要なんですね!
そうそう、安全のための接地や!ところで、なんでB種接地が必要か分かる?もし高圧側と低圧側が混触(ショート)したら何が起こるか想像してみて。めっちゃ危険な状況になるで!
混触が起きたら大変です!高圧(6600Vなど)が低圧側に侵入してきます!
【混触時の危険性】
・通常200Vの機器に高圧がかかる → 機器の破損・火災
・人が触れたら感電死の危険
・低圧側の絶縁が耐えられない
【B種接地の役割】
1. 混触時の対地電圧を150V以下に抑える
2. 地絡電流を大地に逃がす経路を作る
3. 保護装置を確実に動作させる
だから電気設備技術基準では、B種接地の抵抗値が厳格に規定されているんですね。「人命を守る最後の砦」といっても過言ではありません!
その通りや!命を守る重要な設備やねん。さて、問題(a)のB種接地抵抗の上限値を求めよか。電気設備技術基準の解釈第17条に計算式があるんやけど、覚えてる?ヒント:300が出てくるで。
はい!B種接地抵抗の計算式は覚えています!
【B種接地抵抗の基準値】
\[ R_B = \frac{300}{I_g} \, \mathrm{[\Omega]} \]ここで、\( I_g \) は高圧側電路の1線地絡電流です。
この「300」という数字の意味は:
・混触時の対地電圧を150V以下にするため
・安全率2を考慮(150V × 2 = 300)
ただし、1秒以内に遮断する装置があれば「600」、1~2秒なら「300」と、遮断時間によって変わるんです。今回は1.3秒なので「300」を使います!
完璧な理解やな!じゃあ実際に計算してみよか。高圧側の1線地絡電流が5Aやったら、B種接地抵抗の上限値はどうなる?
計算します!
\[ \begin{aligned} R_B &= \frac{300}{I_g} \\[10pt] &= \frac{300}{5} \\[10pt] &= 60 \, \mathrm{[\Omega]} \end{aligned} \]答えは 60Ω です!(選択肢(4))
【確認】
・混触時の対地電圧:\( V = I_g \times R_B = 5 \times 60 = 300 \, \mathrm{[V]} \)
・安全率を考慮した実際の電圧:\( 300 \div 2 = 150 \, \mathrm{[V]} \)
ちょうど150V以下に収まっていますね!これで人が触れても、感電の危険性が大幅に減少します。
よっしゃ!(a)はこれでOKや。次は(b)の問題やけど、これはちょっと難しいで。「B種接地に常時流れる電流」って何やと思う?地絡事故が起きてないのに、なんで電流が流れるんやろ?
あっ、これは対地静電容量があるからですね!
【常時電流が流れる理由】
・各相と大地の間には静電容量 \( C = 0.1 \, \mathrm{\mu F} \) が存在
・交流電圧がかかると、コンデンサを通じて電流が流れる
・これは「充電電流」とも呼ばれます
【イメージ】
・絶縁されていても、わずかに電流が「漏れている」状態
・周波数が高いほど、静電容量が大きいほど電流は増える
・正常運転時でも常に流れている電流
この電流を計算するには、静電容量のリアクタンスと接地抵抗を含む回路解析が必要ですね!
さすが、よく分かってるな!じゃあテブナンの定理を使って解いてみよか。まず、接地抵抗 \( R_B \) を外したときの開放電圧 \( V_0 \) を求めるで。線間電圧200Vから相電圧はどう求める?
三相回路の線間電圧と相電圧の関係から求めます!
【相電圧の計算】
\[ \begin{aligned} V_0 &= \frac{V_{線間}}{\sqrt{3}} \\[10pt] &= \frac{200}{\sqrt{3}} \\[10pt] &= \frac{200}{1.732} \\[10pt] &\approx 115.5 \, \mathrm{[V]} \end{aligned} \]これがB種接地点を外したときの対地電圧(開放電圧)です。
【なぜ√3で割るのか】
・Y結線では、線間電圧 = √3 × 相電圧
・ベクトル図で考えると、120度の位相差があるため
・覚え方:「線間は相の√3倍」
ええやん!次は、電源を短絡したときの等価インピーダンスや。3つの対地静電容量が並列になってるから、容量性リアクタンスはどうなる?ちょっと計算してみて。
3つの静電容量が並列なので、合成容量は3倍になりますね!
【容量性リアクタンスの計算】
1個のコンデンサのリアクタンス:
\[ X_C = \frac{1}{2\pi f C} = \frac{1}{\omega C} \]3個並列の合成リアクタンス:
\[ \begin{aligned} X_0 &= \frac{1}{2\pi f \cdot 3C} \\[10pt] &= \frac{1}{2 \times 3.14159 \times 50 \times 3 \times 0.1 \times 10^{-6}} \\[10pt] &= \frac{1}{314.159 \times 3 \times 10^{-7}} \\[10pt] &= \frac{1}{9.42 \times 10^{-5}} \\[10pt] &\approx 10,610 \, \mathrm{[\Omega]} \end{aligned} \]約10.6kΩという大きな値になりました!これが等価リアクタンスです。
計算バッチリや!10kΩ以上もあるんやな。さて、テブナンの定理で等価回路ができたで。開放電圧115.5V、リアクタンス10,610Ω、接地抵抗10Ω。これらが直列やから、電流はどう計算する?
抵抗とリアクタンスが直列なので、インピーダンスの合成から求めます!
【合成インピーダンス】
\[ \begin{aligned} Z &= \sqrt{R_B^2 + X_0^2} \\[10pt] &= \sqrt{10^2 + 10,610^2} \\[10pt] &= \sqrt{100 + 112,572,100} \\[10pt] &= \sqrt{112,572,200} \\[10pt] &\approx 10,610 \, \mathrm{[\Omega]} \end{aligned} \]おっと、\( R_B = 10\Omega \) は \( X_0 = 10,610\Omega \) に比べて無視できるくらい小さいですね!
【電流の計算】
\[ \begin{aligned} I_B &= \frac{V_0}{Z} \\[10pt] &= \frac{115.5}{10,610} \\[10pt] &\approx 0.0109 \, \mathrm{[A]} \\[10pt] &= 10.9 \, \mathrm{[mA]} \\[10pt] &\approx 11 \, \mathrm{[mA]} \end{aligned} \]答えは 11 mA です!(選択肢(1))
完璧や!ところで、この11mAって大きいと思う?小さいと思う?実は現場では、この充電電流が意外な問題を起こすことがあるんや。どんな問題か想像つく?
11mAは一見小さいですが、実は無視できない電流です!
【充電電流による問題】
1. 漏電遮断器の誤動作
・高感度型(30mA)だと誤動作の可能性
・長い配線ほど静電容量が増えて危険
2. 感電の危険性
・人体の感知電流:約1mA
・苦痛を伴う電流:約5mA
・11mAは十分危険なレベル
3. 絶縁抵抗測定への影響
・メガーで測定時に誤差の原因に
・充電電流を考慮した判定が必要
だから現場では、ケーブルが長い場合は特に注意が必要なんです。インバータ回路では、この充電電流対策が重要な設計ポイントになりますね!
よう知ってるな!実務的な視点も大事やで。最後に、接地工事の種類をまとめとこか。A種、B種、C種、D種、それぞれの抵抗値と用途、覚えてる?これ、電験では必須の知識やで!
接地工事の種類をまとめます!これは暗記必須ですね!
【A種接地工事】
・抵抗値:10Ω以下
・用途:高圧・特別高圧機器の外箱、鉄台
・覚え方:「A(えー)っと、高圧は10Ω」
【B種接地工事】
・抵抗値:変圧器によって計算(今回の問題)
・用途:変圧器の低圧側中性点
・覚え方:「B(ビー)種は変圧器」
【C種接地工事】
・抵抗値:10Ω以下(0.5秒遮断で500Ω以下)
・用途:300V超の低圧機器の外箱
・覚え方:「C(シー)は300V超」
【D種接地工事】
・抵抗値:100Ω以下(0.5秒遮断で500Ω以下)
・用途:300V以下の低圧機器の外箱
・覚え方:「D(でー)んきは低圧100Ω」
語呂合わせ:「アジ(A10)の刺身、ドヒャク(D100)円」なんてのもありますよ!
ははは、その語呂合わせ面白いな!さて、今回の問題でよくある間違いパターンも確認しとこか。特に(b)の計算で、どこでつまずきやすいと思う?
よくある間違いパターンをまとめます:
【問題(a)の間違い】
・遮断時間による係数を間違える(300 vs 600)
・単位を間違える(Aの代わりにmAを使うなど)
・公式を逆にする(\( I_g/300 \) としてしまう)
【問題(b)の間違い】
・線間電圧をそのまま使う(√3で割り忘れ)→ 答えが1.73倍に
・静電容量を1個分で計算(3倍し忘れ)→ 答えが1/3に
・単位変換ミス(μFを10^-6忘れ)→ 桁が大きくずれる
・インピーダンスの合成を間違える(単純な和にしてしまう)
・リアクタンスの公式を間違える(2πを忘れるなど)
【対策】
・単位は必ず確認(特にμ、m、kの変換)
・三相回路は√3の関係を確実に
・計算結果の妥当性を確認(mAオーダーが妥当)
解説まとめ
■ B種接地工事とは
B種接地工事は、高圧電路と低圧電路を結合する変圧器の低圧側中性点に施す接地工事です。高低圧混触時の低圧側の対地電圧上昇を抑制し、感電事故を防止する重要な安全対策です。接地抵抗値は電気設備技術基準により、高圧側の地絡電流と保護装置の動作時間に応じて規定されています。
■ 計算手順と公式
- B種接地抵抗の許容値計算
電気設備技術基準の解釈第17条に基づき、以下の式で算出します。
\( R_B = \frac{150}{I_g} \) または \( R_B = \frac{300}{I_g} \) または \( R_B = \frac{600}{I_g} \)
ここで、\( I_g \):高圧電路の1線地絡電流 [A]、分子の値は遮断時間により決定(1秒以内:150、1~2秒:300、2秒超:600)
- テブナンの定理による等価回路解析
複雑な回路を電圧源と内部インピーダンスの直列回路に置き換えて解析します。
\( I = \frac{V_0}{Z_0 + Z_L} \)
- 対地静電容量のリアクタンス計算
コンデンサのリアクタンスは周波数と静電容量から算出します。
\( X_C = \frac{1}{2\pi fC} \)
■ 具体的な計算例
問題条件
- 低圧側線間電圧:200 V
- 周波数:50 Hz
- 対地静電容量(1相当たり):C = 0.1 μF
- 高圧電路の1線地絡電流:5 A
- 保護装置動作:対地電圧150V超過時、1.3秒で遮断
(a) B種接地抵抗の許容上限値
遮断時間が1.3秒(1秒超2秒以内)なので、以下の計算式を適用します。
\[ \begin{aligned} R_B &= \frac{300}{I_g} \\[5pt] &= \frac{300}{5} \\[5pt] &= 60 \ \mathrm{[\Omega]} \end{aligned} \]結論:B種接地抵抗の許容上限値は 60 Ω(選択肢(4))
(b) 接地抵抗に常時流れる電流の計算
① テブナンの定理による開放電圧の算出:
低圧側の相電圧(対地電圧)を求めます。
\[ \begin{aligned} V_0 &= \frac{V_L}{\sqrt{3}} \\[5pt] &= \frac{200}{\sqrt{3}} \\[5pt] &\approx 115.5 \ \mathrm{[V]} \end{aligned} \]② 3相分の対地静電容量の合成リアクタンス:
3つの対地静電容量が並列接続されているため、合成容量は3Cとなります。
\[ \begin{aligned} X_0 &= \frac{1}{2\pi f \cdot 3C} \\[5pt] &= \frac{1}{2\pi \times 50 \times 3 \times 0.1 \times 10^{-6}} \\[5pt] &= \frac{1}{94.25 \times 10^{-6}} \\[5pt] &\approx 10,610 \ \mathrm{[\Omega]} \end{aligned} \]③ 等価回路の合成インピーダンス:
接地抵抗RBと容量性リアクタンスX0の直列回路となります。
\[ \begin{aligned} Z &= \sqrt{R_B^2 + X_0^2} \\[5pt] &= \sqrt{10^2 + 10,610^2} \\[5pt] &= \sqrt{100 + 112,572,100} \\[5pt] &\approx 10,610 \ \mathrm{[\Omega]} \end{aligned} \]④ 接地抵抗に流れる電流:
\[ \begin{aligned} I_B &= \frac{V_0}{Z} \\[5pt] &= \frac{115.5}{10,610} \\[5pt] &\approx 0.0109 \ \mathrm{[A]} \\[5pt] &\approx 11 \ \mathrm{[mA]} \end{aligned} \]結論:接地抵抗に常時流れる電流は 11 mA(選択肢(1))
■ 実務上の留意点
B種接地工事の設計・施工において、以下の点に注意が必要です。
- 高圧側の地絡電流値は系統の接地方式により大きく異なるため、実測または計算による正確な把握が必要
- 対地静電容量による漏れ電流は、ケーブル長が長いほど大きくなるため、長距離配線では注意が必要
- 保護装置の動作時間設定は、感電保護と系統の安定性のバランスを考慮して決定する
- 接地抵抗値は季節や土壌の状態により変動するため、定期的な測定と管理が重要
- 電気設備技術基準の改正に注意し、最新の規定値を確認することが必要