【法規】令和6年(下期) 問11|流込式水力発電所における溢水日数と年間発電電力量に関する計算問題
最大使用水量 \( 15 \) [m³/s],有効落差 \( 20 \) [m] の流込式水力発電所がある。
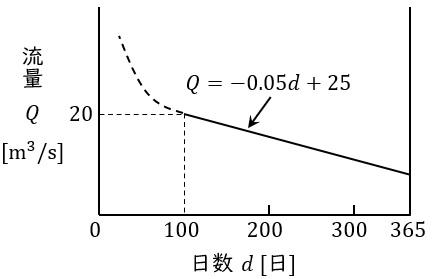
この発電所が利用している河川の流量 \( Q \) が図のような年間流況曲線(日数 \( d \) が \( 100 \) 日以上の部分は,\( Q = -0.05d + 25 \) [m³/s] で表される。)であるとき,次の (a) 及び (b) の問に答えよ。
ただし,水車及び発電機の効率はそれぞれ \( 90 \) [%] 及び \( 95 \) [%] で,流量によって変化しないものとする。
(a) この発電所で年間に溢水(いっすい)が発生する日数の合計として,最も近いのは次のうちどれか。
ただし,溢水とは河川流量を発電に利用しないで無効に放流することをいう。
(b) この発電所の年間可能発電電力量 [GW·h] の値として,最も近いのは次のうちどれか。
合格への方程式
流込式水力発電所の基本原理と出力計算
流込式水力発電所とは?
川の水をそのまま取り入れて発電する方式です。ダムを作らず、自然の流れをそのまま使うので、環境にやさしいんです。でも、川の流量が少ないときは発電量も減ってしまうという特徴があります。
■ 水力発電の出力計算式を理解しよう
水力発電所の出力は、「水の位置エネルギー」を電気エネルギーに変換することで得られます。まず基本となる物理の式から確認していきましょう。
位置エネルギーから電力へ
水の位置エネルギー = 質量 × 重力加速度 × 高さ
これを1秒あたりで考えると、パワー(仕事率)になります。
◆ 基本の出力計算式
水力発電所の理論出力(損失なし)は次の式で表されます:
\[ P_{\text{理論}} = \rho g Q H \quad \mathrm{[W]} \]ここで、
- ρ(ロー)= 水の密度 = 1,000 [kg/m³]
- g = 重力加速度 = 9.8 [m/s²]
- Q = 使用水量 [m³/s](1秒間に流れる水の体積)
- H = 有効落差 [m](実際に発電に使える高さの差)
◆ 実際の発電機出力(効率を考慮)
でも実際は、水車や発電機で必ずエネルギーロスが生じます。そこで効率を掛け算します:
\[ \begin{aligned} P &= \rho g Q H \eta_w \eta_g \quad \mathrm{[W]} \\[10pt] &= 1000 \times 9.8 \times Q \times H \times \eta_w \times \eta_g \quad \mathrm{[W]} \\[10pt] &= 9.8 Q H \eta_w \eta_g \quad \mathrm{[kW]} \end{aligned} \]ここで、
- η_w(イータ・ダブリュー)= 水車効率(通常85~95%)
- η_g(イータ・ジー)= 発電機効率(通常90~98%)
計算例:基本問題の条件で計算してみよう
使用水量 Q = 15 [m³/s]、有効落差 H = 20 [m]、水車効率 = 90%、発電機効率 = 95% のとき
\[ \begin{aligned} P &= 9.8 \times 15 \times 20 \times 0.90 \times 0.95 \\[10pt] &= 9.8 \times 15 \times 20 \times 0.855 \\[10pt] &= 2514 \quad \mathrm{[kW]} \\[10pt] &≒ 2.5 \quad \mathrm{[MW]} \end{aligned} \]約2.5メガワット(2,500世帯分の電力)を発電できることになります!
■ 流込式発電所の特徴をチェック
| 項目 | 流込式 | ダム式・貯水池式 |
|---|---|---|
| 建設コスト | ◎ 安い(ダム不要) | △ 高い(ダム建設必要) |
| 環境への影響 | ◎ 少ない | △ 大きい |
| 発電の安定性 | △ 河川流量に依存 | ◎ 安定(水を貯められる) |
| 溢水の発生 | × 多い(流量が多いとき) | ◎ 少ない(貯水可能) |
| 適した場所 | 流量が安定した河川 | ダム建設可能な地形 |
覚えておきたいポイント
• 流込式は「来た水をそのまま使う」方式
• 最大使用水量を超えた分は溢水(使わずに流す)
• 年間を通じた発電計画が重要になる
年間流況曲線の読み方と特徴
年間流況曲線って何?
1年365日の河川流量を、流量の多い順に並べ替えたグラフです。横軸が日数、縦軸が流量になります。これを見れば、「○○日以上は△△m³/s以上の流量がある」ということが一目でわかるんです!
■ 流況曲線の基本的な見方
年間流況曲線は、発電計画を立てる上で超重要なグラフです。以下の特徴を押さえましょう:
グラフの特徴
• 左側(日数が少ない)= 豊水期(梅雨や台風の時期)
• 右側(日数が多い)= 渇水期(冬や夏の少雨期)
• 曲線は必ず右下がり(日数が増えると流量は減る)
■ 問題で与えられた流況曲線の解析
この問題では、100日以上の部分が直線で近似されています:
\[ Q = -0.05d + 25 \quad \mathrm{[m^3/s]} \quad (d \geq 100) \]この式の意味を理解しましょう:
- 切片 25:d = 0 のときの理論上の流量(実際には使わない)
- 傾き -0.05:日数が1日増えるごとに流量が0.05 m³/s減る
- d = 100 のとき:Q = -0.05×100 + 25 = 20 [m³/s]
- d = 365 のとき:Q = -0.05×365 + 25 = 6.75 [m³/s]
グラフから読み取れること
• 年間で最も流量が少ない日(365日目)でも 6.75 m³/s の流量がある
• 100日目の流量は 20 m³/s
• 最大使用水量 15 m³/s を超える日数を計算できる
■ 流況曲線から読み取る重要な値
| 用語 | 意味 | この問題での値 |
|---|---|---|
| 豊水流量 | 95日流量(上位95日の流量) | 約20.25 m³/s |
| 平水流量 | 185日流量(中央値) | 約15.75 m³/s |
| 低水流量 | 275日流量 | 約11.25 m³/s |
| 渇水流量 | 355日流量(下位10日) | 約7.25 m³/s |
■ 発電計画での活用方法
最大使用水量の決め方
最大使用水量をどこに設定するかで、発電所の経済性が決まります:
• 大きくすると → 設備費が高くなるが、豊水期に多く発電できる
• 小さくすると → 設備費は安いが、溢水が増えて無駄が多い
この問題では最大使用水量が 15 m³/s に設定されています。これがどの程度適切かを次のタブで検証していきます。
試験で注意すること
• 流況曲線の式が与えられたら、必ず端点(d=100, d=365など)の値を計算
• 最大使用水量との交点が溢水日数を決める重要ポイント
• グラフを簡単にスケッチすると間違いが減る
溢水の計算方法と考え方
溢水(いっすい)とは?
河川の流量が発電所の最大使用水量を超えたとき、その超過分の水を発電に使わずに流すことです。もったいないけど、設備の能力には限界があるので仕方ないんです。
■ 溢水が発生する条件
溢水が発生するのは次の条件のときです:
\[ \text{河川流量} Q > \text{最大使用水量} Q_m \]この問題では:
- 最大使用水量 Q_m = 15 [m³/s]
- 河川流量 Q は流況曲線で与えられている
■ 溢水日数の計算手順
Step 1:溢水が発生し始める日数を求める
流況曲線の式 Q = -0.05d + 25 に Q_m = 15 を代入:
\[ \begin{aligned} 15 &= -0.05d_1 + 25 \\[10pt] 0.05d_1 &= 25 - 15 \\[10pt] 0.05d_1 &= 10 \\[10pt] d_1 &= \frac{10}{0.05} = 200 \quad \mathrm{[日]} \end{aligned} \]計算のコツ
0.05 で割るのは、20 を掛けるのと同じ!
d_1 = 10 ÷ 0.05 = 10 × 20 = 200
■ 結果の解釈
d_1 = 200日 という結果から分かること:
- 0~200日:河川流量 > 15 m³/s → 溢水が発生
- 200~365日:河川流量 ≤ 15 m³/s → 溢水なし(全量使用)
したがって、年間の溢水発生日数 = 200日
■ 溢水量の計算(発展)
溢水の総量も計算できます(この問題では不要ですが、理解のために):
ある日(例:d=100)の溢水量
• 河川流量:Q = -0.05×100 + 25 = 20 [m³/s]
• 使用水量:15 [m³/s]
• 溢水量:20 - 15 = 5 [m³/s]
■ 溢水を減らす工夫
| 方法 | メリット | デメリット |
|---|---|---|
| 最大使用水量を増やす | 溢水が減る、発電量増加 | 設備費が高額に |
| 調整池を作る | 一時的に水を貯められる | 建設費増加、環境影響 |
| 揚水発電と組み合わせ | 余剰電力で水を汲み上げ | システムが複雑に |
| 複数の発電所で分担 | 効率的な水利用 | 管理が複雑 |
試験での注意点
• 「溢水が発生する日数」を聞かれているのか「溢水が発生しない日数」を聞かれているのか要確認!
• 流況曲線の式に最大使用水量を代入するだけの簡単な計算
• この問題は絶対に落とせない基本問題です
年間可能発電電力量の詳細計算
年間可能発電電力量とは?
1年間(365日)で発電できる電力量の総計です。単位は [kW·h] や [GW·h] で表します。日々の発電電力に時間を掛けて、それを1年分積み上げた値になります。
■ 計算の基本的な考え方
年間発電電力量を求めるには、流量の変化を考慮する必要があります:
2つの期間に分けて計算
• 期間①(0~200日):最大使用水量で発電(Q = 15 m³/s 一定)
• 期間②(200~365日):河川流量に応じて発電(Q は変化)
■ 期間①:最大使用水量での発電(0~200日)
Step 1:発電電力 P₁ を計算
\[ \begin{aligned} P_1 &= 9.8 \times Q_m \times H \times \eta_w \times \eta_g \\[10pt] &= 9.8 \times 15 \times 20 \times 0.90 \times 0.95 \\[10pt] &= 9.8 \times 15 \times 20 \times 0.855 \\[10pt] &= 2514 \quad \mathrm{[kW]} \end{aligned} \]Step 2:200日間の発電電力量
\[ W_1 = P_1 \times 24 \times 200 = 2514 \times 4800 = 12,067,200 \quad \mathrm{[kW \cdot h]} \]■ 期間②:変動流量での発電(200~365日)
この期間は流量が変化するので、平均流量を使って計算します。
Step 1:期間の両端の流量を確認
• d = 200 のとき:Q = 15 [m³/s](ちょうど最大使用水量)
• d = 365 のとき:Q = -0.05×365 + 25 = 6.75 [m³/s]
Step 2:平均流量を計算
\[ Q_{平均} = \frac{15 + 6.75}{2} = \frac{21.75}{2} = 10.875 \quad \mathrm{[m^3/s]} \]Step 3:平均発電電力 P₂ を計算
\[ \begin{aligned} P_2 &= 9.8 \times 10.875 \times 20 \times 0.90 \times 0.95 \\[10pt] &≒ 1823 \quad \mathrm{[kW]} \end{aligned} \]Step 4:165日間の発電電力量
\[ W_2 = P_2 \times 24 \times 165 = 1823 \times 3960 = 7,219,080 \quad \mathrm{[kW \cdot h]} \]■ 年間可能発電電力量の総計
\[ \begin{aligned} W_{年間} &= W_1 + W_2 \\[10pt] &= 12,067,200 + 7,219,080 \\[10pt] &= 19,286,280 \quad \mathrm{[kW \cdot h]} \\[10pt] &≒ 19.3 \quad \mathrm{[GW \cdot h]} \end{aligned} \]単位変換の確認
• 1 GW·h = 1,000 MW·h = 1,000,000 kW·h
• 19,286,280 kW·h ÷ 1,000,000 = 19.3 GW·h
■ 計算のチェックポイント
| チェック項目 | 確認内容 | この問題での値 |
|---|---|---|
| 期間の合計 | 200日 + 165日 = 365日? | ○ 正しい |
| 出力の大小関係 | P₁ > P₂ になっているか? | ○ 2514 > 1823 |
| 単位の整合性 | kW × h = kW·h になっているか? | ○ 正しい |
| 桁数の妥当性 | GW·h オーダーが妥当か? | ○ 約20 GW·h |
■ より正確な計算方法(参考)
実際には、期間②の流量変化を積分で正確に計算することもできます:
\[ W_2 = 9.8 \times H \times \eta_w \times \eta_g \times 24 \int_{200}^{365} (-0.05d + 25) \, dd \]ただし、電験三種の試験では平均値を使った計算で十分です。積分計算は時間がかかるし、計算ミスのリスクも高くなります。
試験対策のポイント
• この問題は計算量が多いので、時間配分に注意
• (a)は基本問題なので確実に得点する
• (b)は部分点狙いでも、計算過程をしっかり書く
• 電卓の使い方に慣れておく(特に指数計算)
🔍 ワンポイントアドバイス:年間流況曲線の問題は、電験三種でよく出題される重要テーマです。「溢水が発生する日数 = 最大使用水量と流況曲線の交点」という基本を確実に押さえましょう。年間発電電力量の計算は複雑に見えますが、「期間を分けて→それぞれの発電電力を計算→時間を掛けて電力量にする」という手順を守れば必ず解けます。計算ミスを防ぐため、単位と桁数のチェックを忘れずに!
おっ、今日は水力発電の実践的な問題やな!流込式水力発電所って知ってる?これはダムで水を貯めんと、川の水をそのまま使って発電する方式なんや。自然の流れを活かすから環境にもやさしいんやで。まず問題文の条件を整理してみよか。どんな数値が与えられてるか、ひとつずつ確認してみて?
はい、問題文から次の条件を整理します:
・最大使用水量:\( Q_{\mathrm{max}} = 15 \, \mathrm{[m^3/s]} \)
・有効落差:\( H = 20 \, \mathrm{[m]} \)
・水車効率:\( \eta_w = 90\% = 0.90 \)
・発電機効率:\( \eta_g = 95\% = 0.95 \)
・年間流況曲線の式(100日以上):\( Q = -0.05d + 25 \, \mathrm{[m^3/s]} \)
これらの値を使って、溢水が発生する日数と年間可能発電電力量を求める必要がありますね。流況曲線というのは、1年間の河川流量を大きい順に並べたグラフのことです。
そうそう、ええ整理やな!ところで「溢水(いっすい)」って何か分かるか?これ、電験でよく出る重要な用語なんやけど、実は現場でもめっちゃ大切な概念なんや。どういう状況で起こると思う?
溢水とは、河川の流量が発電所の最大使用水量を超えたときに、その超過分を発電に使わずに無効放流することです。
つまり、川の水が \( 15 \, \mathrm{[m^3/s]} \) より多く流れてきても、この発電所では \( 15 \, \mathrm{[m^3/s]} \) までしか使えないので、残りは素通りさせるしかないんです。
例えば、梅雨や台風の時期に川の流量が \( 20 \, \mathrm{[m^3/s]} \) になったら、\( 5 \, \mathrm{[m^3/s]} \) は発電に使えずにもったいない...これが溢水です。でも設備の能力には限界があるので仕方ないんですよね。
その通りや!もったいないけど仕方ないんやな。さて、流況曲線の式をもう一回見てみよか。\( Q = -0.05d + 25 \) って式、これグラフにするとどんな形になるか分かる?傾きが負やから...どうなるんやろな?
傾きが負(-0.05)なので、右下がりの直線グラフになります!
具体的に考えてみると:
・\( d = 100 \) 日のとき:\( Q = -0.05 \times 100 + 25 = 20 \, \mathrm{[m^3/s]} \)
・\( d = 200 \) 日のとき:\( Q = -0.05 \times 200 + 25 = 15 \, \mathrm{[m^3/s]} \)
・\( d = 365 \) 日のとき:\( Q = -0.05 \times 365 + 25 = 6.75 \, \mathrm{[m^3/s]} \)
つまり、日数が増えるほど流量が減っていくグラフです。これは「年間でこの流量以上になる日数」を表していて、大きな流量ほど発生日数が少ないという、実際の河川の特徴をよく表しているんですね。
おお、計算もバッチリやな!でも \( d = 200 \) 日のときちょうど \( 15 \, \mathrm{[m^3/s]} \) になるって気づいた?これ偶然やないで。これが何を意味するか、ピンときた?
あ!これは溢水が発生する境界線ですね!
最大使用水量が \( 15 \, \mathrm{[m^3/s]} \) なので:
・\( d < 200 \) 日の期間:流量が \( 15 \, \mathrm{[m^3/s]} \) を超える → 溢水発生!
・\( d = 200 \) 日:ちょうど \( 15 \, \mathrm{[m^3/s]} \) → ギリギリ全量使える
・\( d > 200 \) 日の期間:流量が \( 15 \, \mathrm{[m^3/s]} \) 未満 → 全量発電に使える
だから、問題(a)の答えは200日なんですね!年間365日のうち200日間は溢水が発生するということです。
完璧や!(a)はこれで解決やな。でも(b)の年間発電電力量はもうちょい複雑やで。まず基本から行こか。水力発電の出力を求める公式、覚えてる?位置エネルギーから考えてみよか。
はい、水力発電の基本公式を導いてみます!
水の位置エネルギーから考えると:
・1秒間に \( Q \, \mathrm{[m^3]} \) の水が流れる
・水の密度 \( \rho = 1000 \, \mathrm{[kg/m^3]} \) なので、質量は \( 1000Q \, \mathrm{[kg]} \)
・高さ \( H \, \mathrm{[m]} \) から落下するので、位置エネルギーは:
\[ \begin{aligned} P_{\text{理論}} &= \rho g Q H \\[10pt] &= 1000 \times 9.8 \times Q \times H \\[10pt] &= 9800QH \, \mathrm{[W]} \\[10pt] &= 9.8QH \, \mathrm{[kW]} \end{aligned} \]実際の出力は効率を考慮して:
\( P = 9.8QH\eta_w\eta_g \, \mathrm{[kW]} \)
素晴らしい導出やな!この \( 9.8 \) って数字、実は重力加速度から来てるんやで。さて、年間発電電力量を求めるには、期間を分けて考える必要があるんや。なんで分ける必要があると思う?
期間を分ける理由は、使用水量が変わるからです!
【期間①:0~200日】
・河川流量 > 15 m³/s だけど、最大使用水量の制限で 15 m³/s しか使えない
・つまり、ずっと定格出力(最大出力)で運転
【期間②:200~365日】
・河川流量 < 15 m³/s なので、流れてきた水を全部使える
・でも流量が日々減っていくので、出力も変化する
この2つの期間で発電の仕方が違うから、別々に計算して合計する必要があるんですね。現場でも、豊水期と渇水期で運転パターンが変わるのと同じ考え方です!
その通り!現場の感覚もバッチリやな。じゃあ、まず期間①(0~200日)の発電電力を計算してみよか。この期間はずっと最大使用水量で運転できるから簡単やで。
期間①(0~200日)の発電電力 \( P_1 \) を計算します:
\[ \begin{aligned} P_1 &= 9.8 \times Q_{\text{max}} \times H \times \eta_w \times \eta_g \\[10pt] &= 9.8 \times 15 \times 20 \times 0.90 \times 0.95 \\[10pt] &= 9.8 \times 15 \times 20 \times 0.855 \\[10pt] &= 147 \times 17.1 \\[10pt] &= 2513.7 \\[10pt] &\approx 2514 \, \mathrm{[kW]} \end{aligned} \]約2.5MWの出力ですね!これを200日間、24時間ずっと維持できるわけです。
この期間の発電電力量は:
\( W_1 = 2514 \times 24 \times 200 = 12,067,200 \, \mathrm{[kWh]} \)
ええ計算や!約12GWhも発電できるんやな。次は期間②(200~365日)やけど、ここがちょっとややこしいで。流量が日々変わるから...どうやって計算したらええと思う?
流量が連続的に変化するので、本来は積分計算が必要ですが...実務的には平均流量を使う方法があります!
期間②の平均流量 \( Q_A \) を求めます:
・始点(d=200日):\( Q = 15 \, \mathrm{[m^3/s]} \)
・終点(d=365日):\( Q = -0.05 \times 365 + 25 = 6.75 \, \mathrm{[m^3/s]} \)
\[ \begin{aligned} Q_A &= \frac{Q_{\text{始}} + Q_{\text{終}}}{2} \\[10pt] &= \frac{15 + 6.75}{2} \\[10pt] &= \frac{21.75}{2} \\[10pt] &= 10.875 \, \mathrm{[m^3/s]} \end{aligned} \]直線的に変化する場合、この平均値を使えば正確な答えが出るんです!これは台形の面積を求める考え方と同じですね。
賢いな!台形の面積の考え方、まさにその通りや。じゃあ、その平均流量を使って期間②の発電電力を計算してみて。さっきと同じ公式使うんやで。
期間②(200~365日)の平均発電電力 \( P_2 \) を計算します:
\[ \begin{aligned} P_2 &= 9.8 \times Q_A \times H \times \eta_w \times \eta_g \\[10pt] &= 9.8 \times 10.875 \times 20 \times 0.90 \times 0.95 \\[10pt] &= 9.8 \times 10.875 \times 20 \times 0.855 \\[10pt] &= 106.575 \times 17.1 \\[10pt] &= 1822.4 \\[10pt] &\approx 1823 \, \mathrm{[kW]} \end{aligned} \]期間②は165日間(365-200=165日)なので、この期間の発電電力量は:
\( W_2 = 1823 \times 24 \times 165 = 7,219,080 \, \mathrm{[kWh]} \)
渇水期になると出力が約72%(1823÷2514)まで落ちるんですね。現場でも渇水期の運転は悩ましいところです。
よっしゃ、あと一歩や!期間①と期間②の発電電力量が出たから、年間の合計を計算してみよか。単位にも気をつけてな。問題では GW·h で答えるんやった。
年間可能発電電力量 \( W \) を計算します:
\[ \begin{aligned} W &= W_1 + W_2 \\[10pt] &= 12,067,200 + 7,219,080 \\[10pt] &= 19,286,280 \, \mathrm{[kWh]} \\[10pt] &\approx 19,300,000 \, \mathrm{[kWh]} \\[10pt] &= 19,300 \, \mathrm{[MWh]} \\[10pt] &= 19.3 \, \mathrm{[GWh]} \end{aligned} \]答えは 19.3 GW·h です!
単位変換のポイント:
・1 MWh = 1,000 kWh
・1 GWh = 1,000 MWh = 1,000,000 kWh
この発電所は年間約19.3GWhの電力を生み出せます。一般家庭約5,400世帯分の年間消費電力に相当しますね!
完璧や!(a)の答えは200日、(b)の答えは19.3 GW·h やな。ところで、この問題から学べる大事なポイントがあるんや。流込式発電所の宿命って何やと思う?
流込式発電所の宿命は「自然の流量に左右される」ことですね!
【メリット】
・ダム建設が不要で初期投資が少ない
・環境への影響が小さい
・保守管理が比較的簡単
【デメリット(宿命)】
・豊水期は溢水でもったいない(この問題では200日間も!)
・渇水期は出力が落ちる(最大の72%まで低下)
・年間を通じて安定した発電ができない
だから実際の電力系統では、貯水池式や揚水式と組み合わせて、お互いの弱点を補い合うんですよね。
電験三種では、この「設備利用率」の考え方もよく出題されます。この発電所の場合、最大出力で365日運転したときと比べて、実際は何%しか発電できていないか...これも重要な指標です!
素晴らしいまとめやな!最後に、この問題でよくある間違いパターンも確認しとこか。実は(b)で計算ミスしやすいポイントがあるんや。どこやと思う?
よくある間違いパターンをまとめます:
【間違い①】期間②で最小流量(6.75 m³/s)だけで計算してしまう
→ 平均流量を使わないと過小評価になります
【間違い②】単位変換ミス
→ kWh → MWh → GWh の変換で1000倍を間違える
【間違い③】24時間をかけ忘れる
→ 出力[kW] × 日数 だけでは時間[h]が足りません
【間違い④】効率をかけ忘れる
→ 水車効率と発電機効率の両方が必要です(0.90×0.95=0.855)
【間違い⑤】9.8の意味を理解せず10で計算
→ 重力加速度は9.8m/s²。10だと約2%の誤差が出ます
電験三種では、こういう「ひっかけ」を避けて確実に得点することが合格への近道です。特に(a)のような単純な問題は絶対に落とさないことが大切ですね!
解説まとめ
■ 流込式水力発電所とは
流込式水力発電所は、河川の自然流量をそのまま利用する発電方式です。ダムによる貯水を行わず、河川流量が最大使用水量を超える場合は溢水(いっすい)として無効放流されます。年間流況曲線を用いて発電計画を立てることが、効率的な運用において重要となります。
■ 計算手順と公式
- 水力発電所の出力計算
水力発電所の発電出力は、使用水量、有効落差、各種効率から算出されます。
\( P = 9.8QH\eta_w\eta_g \ \mathrm{[kW]} \)
ここで、\( Q \):使用水量 \(\mathrm{[m^3/s]}\)、\( H \):有効落差 \(\mathrm{[m]}\)、\( \eta_w \):水車効率、\( \eta_g \):発電機効率
- 流況曲線の解析
年間流況曲線から、溢水が発生する日数を求めます。最大使用水量を超える流量の期間が溢水発生期間となります。
- 年間発電電力量の計算
期間ごとの発電電力に運転時間を乗じて、年間の総発電電力量を算出します。
■ 具体的な計算例
問題条件
- 最大使用水量:\( Q_m = 15 \ \mathrm{m^3/s} \)
- 有効落差:\( H = 20 \ \mathrm{m} \)
- 水車効率:\( \eta_w = 90\% = 0.90 \)
- 発電機効率:\( \eta_g = 95\% = 0.95 \)
- 流況曲線(100日以上):\( Q = -0.05d + 25 \ \mathrm{[m^3/s]} \)
(a) 溢水発生日数の計算
最大使用水量 15 m³/s を超える日数を求めます。
\[ \begin{aligned} Q_m &= -0.05d_1 + 25 \\[5pt] 15 &= -0.05d_1 + 25 \\[5pt] 0.05d_1 &= 10 \\[5pt] d_1 &= 200 \ \mathrm{[日]} \end{aligned} \]結論:溢水発生日数は 200日(選択肢(3))
(b) 年間可能発電電力量の計算
① 0~200日間(最大使用水量で発電)の発電電力:
→
\[ \begin{aligned} P_1 &= 9.8 \times Q_m \times H \times \eta_w \times \eta_g \\[5pt] &= 9.8 \times 15 \times 20 \times 0.90 \times 0.95 \\[5pt] &= 2,514 \ \mathrm{[kW]} \end{aligned} \]② 365日目の流量:
\[ \begin{aligned} Q_L &= -0.05 \times 365 + 25 \\[5pt] &= -18.25 + 25 \\[5pt] &= 6.75 \ \mathrm{[m^3/s]} \end{aligned} \]③ 200~365日間の平均流量:
\[ \begin{aligned} Q_A &= \frac{Q_m + Q_L}{2} \\[5pt] &= \frac{15 + 6.75}{2} \\[5pt] &= 10.875 \ \mathrm{[m^3/s]} \end{aligned} \]④ 200~365日間の平均発電電力:
\[ \begin{aligned} P_2 &= 9.8 \times Q_A \times H \times \eta_w \times \eta_g \\[5pt] &= 9.8 \times 10.875 \times 20 \times 0.90 \times 0.95 \\[5pt] &= 1,823 \ \mathrm{[kW]} \end{aligned} \]⑤ 年間可能発電電力量:
\[ \begin{aligned} W &= P_1 \times 24 \times 200 + P_2 \times 24 \times (365-200) \\[5pt] &= 2,514 \times 24 \times 200 + 1,823 \times 24 \times 165 \\[5pt] &= 12,067,200 + 7,219,080 \\[5pt] &= 19,286,280 \ \mathrm{[kWh]} \\[5pt] &\approx 19.3 \ \mathrm{[GWh]} \end{aligned} \]結論:年間可能発電電力量は 19.3 GWh(選択肢(1))
■ 実務上の留意点
流込式水力発電所の設計・運用において、以下の点に注意が必要です。
- 河川流量の季節変動を考慮した最大使用水量の設定が経済性に大きく影響する
- 溢水期間が長すぎると設備利用率が低下するため、適切な設備容量の選定が重要
- 流況曲線の分析では、平均流量ではなく、実際の流量変化を考慮した積分計算が必要
- 実際の運用では、保守点検による停止期間も考慮する必要がある