【理論】令和6年 (下期) 問10|RL回路の過渡現象におけるスイッチ投入直後と定常時の電流比計算問題
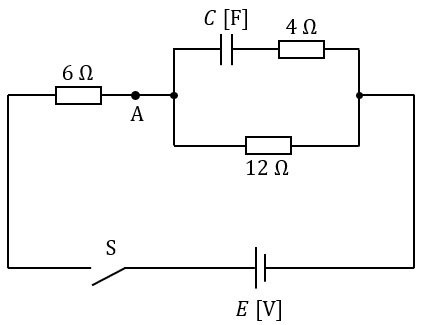
図に示す回路において,スイッチ \( S \) を閉じた瞬間(時刻 \( t = 0 \))に点 \( A \) を流れる電流を \( I_0 \) [A] とし,十分に時間が経ち,定常状態に達したのちに点 \( A \) を流れる電流を \( I \) [A] とする。
電流比 \( \displaystyle \frac{I_0}{I} \) の値として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
ただし,コンデンサの初期電荷は零とする。
合格への方程式
問題と基本概念
重要なポイント
- コンデンサは時間によって状態が大きく変わる
- 瞬間的:短絡状態(電流が流れやすい)
- 十分時間経過後:開放状態(電流が流れない)
- 回路の合成抵抗の変化を正しく計算する
過渡現象とは
過渡現象とは、スイッチを入れた瞬間から回路が安定するまでの間に起こる現象のことです。コンデンサやコイルがある回路では、この現象が特に重要になります。
身近な例で考えてみよう
コンデンサは「電気のダム」のようなものです。ダムが空っぽの時(初期状態)は水がどんどん流れ込みますが、ダムが満杯になると(定常状態)水は流れなくなります。コンデンサも同じで、最初は電流がどんどん流れますが、電荷が溜まってくると電流が流れなくなります。
問題を解くための準備
この問題を解くには、以下の2つの状態を理解する必要があります:
2つの重要な状態
- 瞬間的(t=0):コンデンサが短絡状態
- 定常状態(t→∞):コンデンサが開放状態
それぞれの状態で回路図を描き直し、合成抵抗を計算して電流を求めます。
コンデンサの状態変化
コンデンサの状態は時間とともに以下のように変化します:
- スイッチを入れた瞬間:コンデンサは空っぽなので、電流がどんどん流れる(短絡状態)
- 時間が経つにつれて:コンデンサに電荷が溜まり、流れる電流が減っていく
- 十分時間が経過:コンデンサが満杯になり、電流が流れなくなる(開放状態)
よくある間違い
- コンデンサの状態(短絡・開放)を逆に覚えてしまう
- 並列と直列の合成抵抗の公式を混同する
- 電流比を逆に計算してしまう
- 初期電荷がゼロという条件を忘れる
回路の基本的な考え方
この問題では、同じ回路でも時間によって等価回路が変わります:
- 瞬間的:コンデンサを導線(短絡)として考える
- 定常状態:コンデンサを切断(開放)として考える
それぞれの等価回路で合成抵抗を求め、オームの法則で電流を計算します。
過渡現象の基礎知識
コンデンサの過渡現象
コンデンサの過渡現象を理解するために、まずコンデンサの基本的な性質を確認しましょう。
コンデンサの基本式
\[ i = C \frac{dv}{dt} \]ここで、\( i \):電流、\( C \):静電容量、\( v \):電圧、\( t \):時間
過渡状態と定常状態の詳しい説明
① 過渡状態(瞬間的な状態)
スイッチを入れた瞬間、コンデンサの電圧は急に変わることができません。初期電荷がゼロなので、コンデンサの電圧は0Vのままです。
なぜ短絡状態になるのか
コンデンサの電圧が0Vということは、コンデンサの両端が同じ電位ということです。これは導線でつながっているのと同じ状態、つまり短絡です。
② 定常状態(十分時間が経過した状態)
十分時間が経つと、コンデンサは完全に充電され、それ以上電流が流れなくなります。
なぜ開放状態になるのか
コンデンサが満杯になると、これ以上電荷を蓄えることができません。電流が流れないということは、回路が切断されているのと同じ状態、つまり開放です。
コイル(リアクトル)の場合(参考)
コイルの場合は、コンデンサとは逆の動作をします:
→ 横スクロールして下さい →
| 素子 | 過渡状態(瞬間) | 定常状態(十分経過後) |
|---|---|---|
| コンデンサ | 短絡(電流が流れやすい) | 開放(電流が流れない) |
| コイル | 開放(電流が流れない) | 短絡(電流が流れやすい) |
覚え方のコツ
「コンデンサは最初だけ頑張る(短絡→開放)」「コイルは後から頑張る(開放→短絡)」と覚えると分かりやすいです。
合成抵抗の計算方法
抵抗 \( R_1 \, \mathrm{[\Omega]} \) と \( R_2 \, \mathrm{[\Omega]} \) が与えられている時,それぞれの合成抵抗 \( R \, \mathrm{[\Omega]} \) は以下の式で与えられます。
①直列接続
抵抗が一列に並んでいる場合:
\[ R = R_1 + R_2 \]②並列接続
抵抗が並行に配置されている場合:
\[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \]整理すると:
\[ R = \frac{R_1 R_2}{R_1 + R_2} \]並列抵抗の計算例
4Ωと12Ωの並列:
\[ R = \frac{4 \times 12}{4 + 12} = \frac{48}{16} = 3 \, \Omega \]時定数と過渡応答
実際の過渡現象では、瞬間的に変化するのではなく、指数関数的に変化します。
時定数τ
\[ \tau = RC \]時定数は、コンデンサの充放電にかかる時間の目安です。
実際の変化
- 1τ後:約63%変化
- 3τ後:約95%変化
- 5τ後:約99%変化(ほぼ完了)
電流と電圧の時間変化
RC回路の過渡現象では、電流と電圧が以下のように変化します:
→ 横スクロールして下さい →
\[ \begin{aligned} i(t) &= I_0 e^{-t/\tau} \\[10pt] v_C(t) &= V(1 - e^{-t/\tau}) \end{aligned} \]ここで、\( I_0 \):初期電流、\( V \):電源電圧、\( \tau \):時定数
実際の解き方・計算手順
与えられた条件の整理
問題の条件
- 回路には6Ω、4Ω、12Ωの抵抗とコンデンサがある
- コンデンサの初期電荷はゼロ
- スイッチを閉じた瞬間の電流を \( I_0 \)
- 定常状態の電流を \( I \)
- 求めるもの:電流比 \( \frac{I_0}{I} \)
ステップ1:瞬間的な状態の回路を考える
スイッチを閉じた瞬間、コンデンサは短絡状態になります。

この状態では、4Ωと12Ωの抵抗が並列接続され、それが6Ωの抵抗と直列接続されています。
並列部分の合成抵抗
\[ R_{並列} = \frac{4 \times 12}{4 + 12} = \frac{48}{16} = 3 \, \Omega \]回路全体の合成抵抗
\[ R_0 = 6 + 3 = 9 \, \Omega \]瞬間的な電流 \( I_0 \)
\[ I_0 = \frac{E}{R_0} = \frac{E}{9} \, \mathrm{[A]} \]計算のポイント
並列抵抗の計算では「積を和で割る」、直列抵抗では「単純に足す」ことを確実に覚えておきましょう。
ステップ2:定常状態の回路を考える
十分時間が経過すると、コンデンサは開放状態になります。

この状態では、コンデンサに電流が流れないので、12Ωの抵抗には電流が流れません。したがって、6Ωと4Ωの抵抗のみが直列接続された回路として考えます。
回路全体の合成抵抗
\[ R = 6 + 12 = 18 \, \Omega \]なぜ6+12なのか
コンデンサが開放状態なので、電流は6Ω → 12Ωの経路のみを通ります。4Ωの抵抗は、コンデンサによって回路から切り離されています。
定常状態の電流 \( I \)
\[ I = \frac{E}{R} = \frac{E}{18} \, \mathrm{[A]} \]ステップ3:電流比を計算する
求める電流比 \( \frac{I_0}{I} \) は:
\[ \begin{aligned} \frac{I_0}{I} &= \frac{\frac{E}{9}}{\frac{E}{18}} \\[10pt] &= \frac{E}{9} \times \frac{18}{E} \\[10pt] &= \frac{18}{9} \\[10pt] &= 2.0 \end{aligned} \]計算の確認
電流比は合成抵抗の比の逆数になることを確認:
\[ \frac{I_0}{I} = \frac{R}{R_0} = \frac{18}{9} = 2.0 \quad \checkmark \]結果の物理的解釈
結果の意味
- 瞬間的:合成抵抗9Ω、電流 \( \frac{E}{9} \)
- 定常状態:合成抵抗18Ω、電流 \( \frac{E}{18} \)
- 電流比:2.0(瞬間的な電流の方が2倍大きい)
なぜ瞬間的な電流の方が大きいのか
瞬間的にはコンデンサが短絡状態なので、より多くの電流経路があります。定常状態ではコンデンサが開放状態になり、電流経路が制限されるため、回路全体の抵抗が大きくなり、電流が小さくなります。
簡単な解法(上級者向け)
電圧が同じ場合、電流比は合成抵抗の比の逆数になることを利用すると:
\[ \frac{I_0}{I} = \frac{R}{R_0} = \frac{18}{9} = 2.0 \]このように、わざわざ電流を求めなくても、合成抵抗の比から直接答えを求めることができます。
答え:(4) \( 2.0 \)
応用と発展的な考え方
類似問題のパターン
過渡現象の問題には以下のような様々なパターンがあります:
パターン1:RL回路
コイルがある回路では、瞬間的に開放、定常状態で短絡として考えます。
パターン2:RLC回路
コイルとコンデンサが両方ある場合は、それぞれの状態を組み合わせて考えます。
パターン3:スイッチの切り替え
スイッチを開いたり閉じたりする場合の過渡現象も重要です。
実際の応用分野
| 応用分野 | 過渡現象の役割 | 重要性 |
|---|---|---|
| 電源回路 | 起動時の電流制限 | 素子保護のため |
| モータ制御 | 始動電流の抑制 | 配線容量の適正化 |
| タイマー回路 | 遅延時間の生成 | 制御タイミングの調整 |
| フィルタ回路 | ノイズ除去特性 | 信号品質の向上 |
| 発振回路 | 振動の開始条件 | 安定した発振のため |
| 保護回路 | 異常検出と遮断 | 機器の安全確保 |
実際の時間変化の様子
実際の過渡現象では、電流は瞬間的に変化するのではなく、指数関数的に変化します:
RC回路の電流変化
\[ i(t) = I_0 e^{-t/\tau} \]ここで、\( \tau = RC \)(時定数)
時間変化の特徴
- t = 0:電流は最大値 \( I_0 \)
- t = τ:電流は約37%に減少
- t = 3τ:電流は約5%に減少
- t → ∞:電流は定常値 \( I \) に収束
エネルギーの観点から見た過渡現象
過渡現象では、エネルギーの蓄積と放出が重要な役割を果たします:
エネルギーの蓄積
- コンデンサ:\( W_C = \frac{1}{2}CV^2 \)(電界エネルギー)
- コイル:\( W_L = \frac{1}{2}LI^2 \)(磁界エネルギー)
設計上の考慮事項
実際の回路設計での注意点
- 突入電流:スイッチ投入時の大電流による素子破壊
- 電圧サージ:急激な電圧変化による絶縁破壊
- 振動現象:LC回路での減衰振動
- 熱問題:過渡電流による発熱
- 電磁干渉:急激な電流変化によるノイズ
測定と確認方法
過渡現象は以下の方法で観測・測定できます:
- オシロスコープ:電圧・電流波形の時間変化を観測
- データロガー:長時間の変化を記録
- シミュレーション:SPICE等の回路シミュレータ
- 理論計算:微分方程式による解析
実験での確認
実際の回路で過渡現象を確認する場合:
- RC回路を組み、オシロスコープを接続
- ファンクションジェネレータで矩形波を入力
- コンデンサ電圧の充放電波形を観測
- 時定数τと理論値を比較
発展的な解析手法
高度な解析方法
- ラプラス変換:s領域での解析
- 状態方程式:行列を使った表現
- 伝達関数:入出力の関係を関数で表現
- 極・零点解析:システムの安定性評価
- 過渡応答解析:ステップ応答、インパルス応答
実用回路での過渡現象対策
実際の回路では、過渡現象による問題を防ぐための対策が重要です:
対策例
- ソフトスタート回路:徐々に電圧を上昇
- サージ吸収素子:バリスタやツェナーダイオード
- スナバ回路:RC、RCDスナバによる保護
- 電流制限抵抗:突入電流の抑制
- 遅延回路:タイミング調整
学習の発展方向
次のステップへ
- 微分方程式:過渡現象の数学的解法
- 複素数解析:交流回路との関連
- 制御工学:フィードバック制御の基礎
- 電力エレクトロニクス:スイッチング回路の応用
- 信号処理:ディジタルフィルタとの関連
過渡現象の実用的な応用例
日常生活でも過渡現象は身近なところで活用されています:
身近な応用例
- カメラのフラッシュ:コンデンサの急速放電
- 電子レンジ:マグネトロンの起動制御
- 蛍光灯:点灯管による始動
- 自動車:イグニッションコイルの高電圧発生
- 除細動器:心臓への電気ショック
問題解決のコツ
効率的な解法のポイント
- 状態の確認:瞬間的か定常状態かを明確にする
- 等価回路:コンデンサ・コイルの状態を正しく置き換える
- 合成抵抗:並列・直列の計算を間違えない
- 比例関係:電流比は抵抗比の逆数を活用
- 物理的解釈:結果が常識的に正しいか確認
よくある出題パターンと対策
第3種電気主任技術者試験では、以下のような出題が多く見られます:
出題傾向と対策
- 電流比・電圧比:瞬間と定常の比較問題
- 時定数計算:充放電時間の推定
- エネルギー問題:蓄積エネルギーの計算
- 複合回路:複数のRC要素を含む回路
- 実用問題:モータ始動、保護回路等
計算ミスを防ぐためのチェックポイント
見直しのポイント
- 単位の確認:Ω、A、V、s等の単位が正しいか
- 桁数の確認:計算結果の桁数が妥当か
- 極端値の確認:t=0とt=∞での値が正しいか
- 物理的妥当性:結果が物理法則に合っているか
- 選択肢との比較:計算結果が選択肢に近いか
実験による理解の深化
理論だけでなく、実際の実験で過渡現象を体感することが重要です:
簡単な実験例
- 準備:抵抗、コンデンサ、LED、電池、スイッチ
- 回路組立:RC直列回路にLEDを接続
- 観察:スイッチ投入時のLEDの明るさ変化
- 測定:オシロスコープでの電圧波形観測
- 比較:理論値と実測値の比較
関連する他の現象
過渡現象の理解は、他の電気現象の理解にも役立ちます:
| 関連現象 | 共通点 | 応用分野 |
|---|---|---|
| 共振現象 | LCの組み合わせ | 無線通信、フィルタ |
| インパルス応答 | システムの特性 | 信号処理、制御 |
| 安定性解析 | 極・零点の配置 | 制御システム |
| 周波数応答 | 複素インピーダンス | フィルタ設計 |
最新技術での応用
現代の先端技術でも過渡現象の理解は重要です:
最新応用例
- 電気自動車:バッテリー充放電制御
- 太陽光発電:MPPT制御の動特性
- スマートグリッド:電力系統の安定性
- IoT機器:低消費電力設計
- 5G通信:高速スイッチング回路
学習効果を高めるための演習
練習問題例
- RC回路で時定数が2倍になったとき、過渡時間はどう変わるか?
- RL回路とRC回路の過渡現象の違いを説明せよ
- 複数のコンデンサがある回路での等価回路を描け
- 実際のモータ始動回路での突入電流を推定せよ
学習のまとめ
RC回路の過渡現象は、電気回路の基本でありながら、実用的な応用範囲も広い重要な分野です。「瞬間的には短絡、定常的には開放」というコンデンサの基本特性を確実に理解し、合成抵抗の計算を正確に行えれば、複雑な回路でも必ず解けるようになります。また、この基礎知識は制御工学、電力エレクトロニクス、信号処理など、より高度な分野への発展の土台となります。
🔍 ワンポイントアドバイス: RC回路の過渡現象問題は「コンデンサの状態変化」を正しく理解することが最重要です。「瞬間的には短絡、定常的には開放」というコンデンサの基本特性を確実に覚え、それぞれの状態で等価回路を正しく描けるようになりましょう。計算手順は①瞬間的な状態の合成抵抗を求める、②定常状態の合成抵抗を求める、③電流比は抵抗比の逆数、の3ステップです。並列抵抗の計算(積を和で割る)を間違えやすいので、特に注意しましょう。また、結果が物理的に妥当か確認する習慣をつけることで、計算ミスを防げます。この基本パターンは、電源回路、モータ制御、タイマー回路など実用回路の理解にも直結する重要な知識です。
今度は過渡現象の問題やで!これは電験三種の中でも特に重要な分野や。
スイッチを入れた瞬間と、十分時間が経った後で、コンデンサの性質がガラッと変わるんや。この変化を理解できれば、電気回路の本質が見えてくるで!

この回路で、スイッチを閉じた瞬間と定常状態で、点Aを流れる電流がどう変化するかを求める問題やな。まず、何が起こるか想像できるかな?
【問題の構成と求めるもの】
与えられた回路:
・6Ωの抵抗(スイッチと直列)
・4Ωの抵抗とコンデンサが直列
・12Ωの抵抗
・4Ω+コンデンサと12Ωが並列接続
・全体が6Ωと直列接続
求めるもの:
・\( t = 0 \)(スイッチを閉じた瞬間)の点Aの電流:\( I_0 \)
・十分時間が経過した定常状態の点Aの電流:\( I \)
・電流比:\( \frac{I_0}{I} \)
重要な条件:
コンデンサの初期電荷は零(完全に放電された状態からスタート)
解法のポイント:
コンデンサの過渡状態と定常状態での性質の違いを理解することが最重要です。
よし、問題の構成は理解できたな!そしたら過渡現象の基本を確認しておこう。
コンデンサっていうのは、スイッチを入れた瞬間と十分時間が経った後で、まったく違う振る舞いをするんや。これが過渡現象の核心やで。どんな違いがあるか知ってるか?
【コンデンサの過渡現象における基本性質】
1. 過渡状態(\( t = 0 \)の瞬間)
・コンデンサの初期電荷が零の場合
・コンデンサは「短絡」として動作
・理由:電荷を蓄えようとして大量の電流が流れるため
・実質的にコンデンサ部分は導線と同じ状態
2. 定常状態(十分時間経過後)
・コンデンサが完全に充電された状態
・コンデンサは「開放」として動作
・理由:これ以上電荷を蓄えられないため、電流が流れない
・実質的にコンデンサ部分は断線と同じ状態
【覚え方のコツ】
・最初:コンデンサは「短絡」(ショート)
・最後:コンデンサは「開放」(オープン)
・「ショート → オープン」と覚える
【参考:リアクトル(コイル)の場合】
・最初:「開放」(電流の変化を嫌がる)
・最後:「短絡」(抵抗が零になる)
コンデンサとは逆の性質を持ちます。
完璧や!コンデンサの基本性質が理解できたな。そしたら実際に回路を解析してみよう。
まずは \( t = 0 \) の瞬間から始めるで。この瞬間、コンデンサは短絡として動作するから、回路がどう変化するか見てみよか。

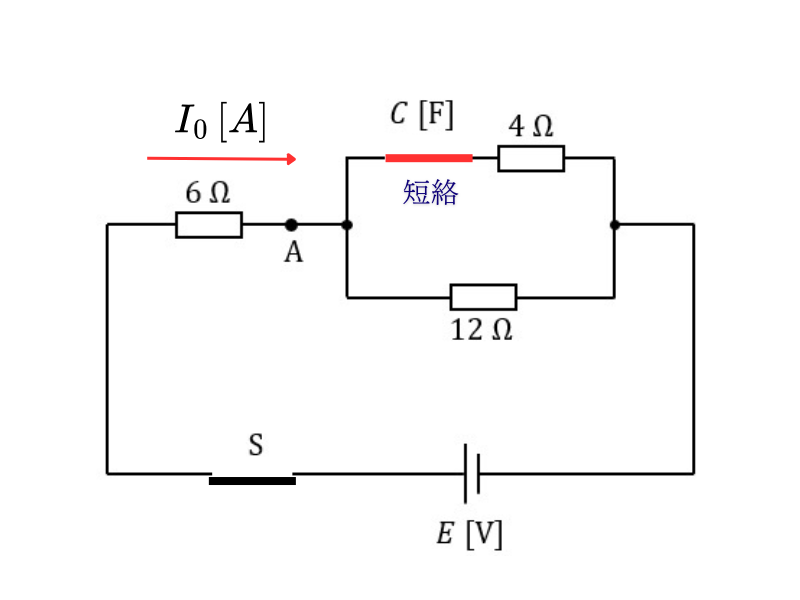
【ステップ1:\( t = 0 \) 時の回路解析】
回路の変化:
コンデンサが短絡することで:
・4Ωの抵抗とコンデンサの直列回路 → 4Ωの抵抗のみ
・この4Ωと12Ωが並列接続
・全体として6Ωと(4Ω || 12Ω)の直列接続
並列抵抗の計算:
4Ωと12Ωの並列合成抵抗:
→ 横スクロールして下さい →
\[ \begin{aligned} R_{並列} &= \frac{4 \times 12}{4 + 12} \\[10pt] &= \frac{48}{16} \\[10pt] &= 3 \, \mathrm{[\Omega]} \end{aligned} \]回路全体の合成抵抗:
→ 横スクロールして下さい →
\[ \begin{aligned} R_0 &= 6 + 3 \\[10pt] &= 9 \, \mathrm{[\Omega]} \end{aligned} \]よし!\( t = 0 \) のときの合成抵抗が9Ωって求まったな。そしたらオームの法則で電流を求めてみよう。
電源電圧を \( E \) とすると、点Aを流れる電流 \( I_0 \) はどうなるかな?
【ステップ2:\( t = 0 \) 時の電流計算】
オームの法則を適用:
→ 横スクロールして下さい →
\[ \begin{aligned} I_0 &= \frac{E}{R_0} \\[10pt] &= \frac{E}{9} \, \mathrm{[A]} \end{aligned} \]【電流の意味】
この電流 \( I_0 = \frac{E}{9} \) は:
・電源から点Aを通って流れる全電流
・コンデンサが短絡状態なので比較的大きな電流
・並列回路により電流は4Ωと12Ωの経路に分流される
【次のステップへの準備】
次に定常状態(\( t = \infty \))での電流を求めて、比較します。
定常状態ではコンデンサが開放となり、回路構成が大きく変わります。
よし、\( I_0 \) が求まったな!そしたら次は定常状態を見てみよう。
十分時間が経つと、コンデンサは開放として動作するんや。つまり、コンデンサの部分は電流が流れへん状態になるんやで。

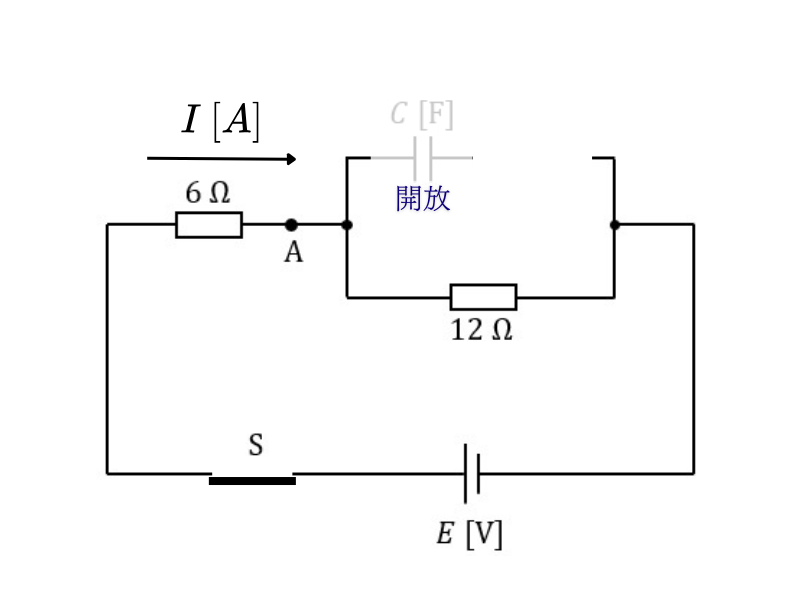
【ステップ3:定常状態(\( t = \infty \))の回路解析】
回路の変化:
コンデンサが開放することで:
・4Ωとコンデンサの直列回路には電流が流れない
・電流は12Ωの経路のみを通る
・実質的に6Ωと12Ωの直列回路となる
回路構成の理解:
・上側の経路(4Ω + コンデンサ):電流零
・下側の経路(12Ω):全電流が流れる
・全体:6Ω + 12Ωの直列接続
回路全体の合成抵抗:
→ 横スクロールして下さい →
\[ \begin{aligned} R &= 6 + 12 \\[10pt] &= 18 \, \mathrm{[\Omega]} \end{aligned} \]【重要なポイント】
並列回路の一方が開放されると、その経路には電流が流れなくなります。
完璧や!定常状態の合成抵抗が18Ωになったな。そしたらこの状態の電流も求めてみよう。
同じ電圧 \( E \) やけど、抵抗が9Ωから18Ωに変わったから、電流はどう変化するかな?
【ステップ4:定常状態の電流計算】
オームの法則を適用:
→ 横スクロールして下さい →
\[ \begin{aligned} I &= \frac{E}{R} \\[10pt] &= \frac{E}{18} \, \mathrm{[A]} \end{aligned} \]【電流の比較】
・過渡状態(\( t = 0 \)):\( I_0 = \frac{E}{9} \, \mathrm{[A]} \)
・定常状態(\( t = \infty \)):\( I = \frac{E}{18} \, \mathrm{[A]} \)
【変化の傾向】
・合成抵抗:9Ω → 18Ω(2倍に増加)
・電流:\( \frac{E}{9} \) → \( \frac{E}{18} \)(半分に減少)
【物理的意味】
最初はコンデンサが電流を通すため電流が大きく、時間が経つとコンデンサが電流を遮断するため電流が小さくなります。
よっしゃ!そしたら最後に電流比を計算してみよう。
\( I_0 = \frac{E}{9} \) と \( I = \frac{E}{18} \) が分かったから、\( \frac{I_0}{I} \) を求めるだけやな。分数の割り算やから、気をつけて計算してや〜
【ステップ5:電流比の計算】
求める電流比:
→ 横スクロールして下さい →
\[ \begin{aligned} \frac{I_0}{I} &= \frac{\frac{E}{9}}{\frac{E}{18}} \\[15pt] &= \frac{E}{9} \times \frac{18}{E} \\[10pt] &= \frac{E \times 18}{9 \times E} \\[10pt] &= \frac{18}{9} \\[10pt] &= 2.0 \end{aligned} \]【計算の確認】
別の考え方:抵抗比の逆数
→ 横スクロールして下さい →
\[ \frac{I_0}{I} = \frac{R}{R_0} = \frac{18}{9} = 2.0 \]【結果の解釈】
・過渡状態の電流は定常状態の電流の2倍
・これはコンデンサの短絡→開放変化による効果
・選択肢(4) 2.0 が正解
完璧や!答えは (4) 2.0 やな。でも計算だけやなくて、この結果が物理的に妥当かどうかも確認してみよう。
過渡状態の電流が定常状態の2倍っていうのは、理論的に正しいかな?コンデンサの性質から考えてみよか。
【結果の妥当性確認】
1. 物理的な理解
・過渡状態:コンデンサが短絡 → より多くの電流経路 → 大きな電流
・定常状態:コンデンサが開放 → 限られた電流経路 → 小さな電流
✓ \( I_0 > I \) となるのは理論的に正しい
2. 数値の妥当性
・合成抵抗の変化:9Ω → 18Ω(2倍)
・電流の変化:2倍 → 1倍(1/2倍)
・電流比:2.0倍
✓ 抵抗が2倍になれば電流は1/2倍になり、比は2.0となる
3. 極限ケースでの確認
・もし並列抵抗が無限大なら:電流比は無限大
・もし並列抵抗が零なら:電流比は1.0
・実際は中間的な値(2.0)→ 妥当
4. エネルギー的考察
・過渡状態:コンデンサへの充電エネルギーが必要
・定常状態:充電完了で追加エネルギー不要
✓ 過渡状態で大きな電流が必要なのは自然
素晴らしい!理論的にも完璧やな。そしたら他の選択肢がなんでダメなのかも確認してみよう。
どんな間違いをすると他の値になってしまうかを理解しておけば、同じミスを避けられるからな。
【他の選択肢の検討】
選択肢(1) 0.5:電流比が逆
\( \frac{I}{I_0} = \frac{1}{2} = 0.5 \) を計算してしまった場合。分子と分母を逆にした間違い。
選択肢(2) 1.0:変化なし
コンデンサの過渡現象を無視した場合。「抵抗だけの回路だから電流は変わらない」という間違った理解。
選択肢(3) 1.5:計算ミス
並列抵抗の計算や合成抵抗の計算で数値を間違えた場合。例えば並列抵抗を4Ωで計算してしまうなど。
選択肢(4) 2.0:正解
✓ 正しい計算結果
選択肢(5) 2.5:計算ミス
何らかの数値計算間違い。または回路構成の読み違え。
【よくある間違いパターン】
・コンデンサの過渡・定常特性の混同
・並列抵抗の計算ミス
・電流比の分子分母の取り違え
・回路図の読み違え
よっしゃ!間違いパターンも理解できたな。そしたら、この問題で重要な「効率的な解法」も教えたるわ。
実は、電圧が同じやったら抵抗比と電流比は逆数の関係にあるんや。これを知ってたら、もっと早く解けるで!
【効率的な解法:抵抗比と電流比の関係】
基本原理:
同じ電圧 \( E \) に対して:
→ 横スクロールして下さい →
\[ \frac{I_0}{I} = \frac{\frac{E}{R_0}}{\frac{E}{R}} = \frac{E}{R_0} \times \frac{R}{E} = \frac{R}{R_0} \]【今回の問題への適用】
1. 過渡状態の合成抵抗:\( R_0 = 9 \, \mathrm{[\Omega]} \)
2. 定常状態の合成抵抗:\( R = 18 \, \mathrm{[\Omega]} \)
3. 電流比:\( \frac{I_0}{I} = \frac{R}{R_0} = \frac{18}{9} = 2.0 \)
【この方法の利点】
・電流を具体的に計算する必要がない
・抵抗比だけで答えが求まる
・計算ミスが減る
・時間短縮になる
【一般化】
過渡現象問題では:
1. 過渡状態と定常状態の等価回路を描く
2. 各状態の合成抵抗を求める
3. 抵抗比の逆数が電流比
ナイス!効率的な解法も理解できたな。そしたら、この問題で学んだ過渡現象の知識を実際の電気回路でどう活かせるかも考えてみよう。
過渡現象は電子回路や電力系統で非常に重要やからな。どんな場面で今日の知識が役立つと思う?
過渡現象について学んで、これが実際の電気回路でとても重要だということが分かりました。
特に印象的だったのは、スイッチを入れた瞬間と安定した後で、コンデンサの性質が「短絡」から「開放」に完全に変わることです。これは実際の回路設計でも重要な考慮事項になりそうです。
例えば、電源を入れた瞬間の「突入電流」という現象があると聞いたことがありますが、これも今日学んだ過渡現象の一種でしょうか。コンデンサが最初に短絡として動作するため、大きな電流が流れるということですね。
また、フィルタ回路や電源の平滑回路でも、コンデンサの充放電特性が重要になると思います。定常状態での動作だけでなく、起動時の過渡状態も考慮する必要があるということですね。
タイマー回路やパルス回路でも、コンデンサの充放電を利用した時定数の概念が関係していそうです。今日の「短絡→開放」の変化を時間軸で考えると、様々な応用が見えてきます。
おお、素晴らしい洞察や!まさにその通りやで。
突入電流の話、これは今日学んだ内容そのものや。電源を入れた瞬間、コンデンサが短絡として動作するから、ヒューズが飛んだりブレーカーが落ちたりすることがあるんや。だから実際の設計では「ソフトスタート回路」を入れたりするんやで。
それから君が言ったタイマー回路、これもRC時定数を使った回路やな。\( \tau = RC \) っていう時定数で、コンデンサの充放電時間が決まるんや。今日の基礎があれば、時定数の計算も理解できるようになるで。
電力系統でも、送電線の投入時に起こる過渡現象とか、変圧器の励磁突入電流とか、いろんなところで過渡現象が関係してくるんやで〜
先生の説明で、過渡現象がこんなに重要で身近なものだと分かりました!
ソフトスタート回路という解決策があるのも興味深いです。突入電流を防ぐために、意図的にゆっくりと電圧を上げていく技術なのでしょうね。
RC時定数 \( \tau = RC \) という概念も初めて知りました。今日学んだ「短絡→開放」の変化が、実際には指数関数的な変化で、その時間スケールがRC時定数で決まるということですね。
電力系統での送電線投入時の過渡現象や変圧器の励磁突入電流というのは、さらに大規模な応用例ですね。家庭レベルから電力系統レベルまで、今日学んだ基本原理が共通して使われているということに驚きます。
今まで過渡現象は難しそうだと思っていましたが、「コンデンサは最初短絡、最後開放」という基本を覚えれば、様々な問題に応用できることが分かりました。
実際の回路を見るときも、「この回路でスイッチを入れたらどうなるか?」という視点で考えるようになりそうです!
その通りや!その視点を持ち続けてくれたら、電気回路の理解がどんどん深まるで。
そしたら最後に、この問題から派生して覚えておくべき「電験三種での頻出パターン」をまとめとこう。過渡現象は毎年必ず出る重要分野やからな!
【電験三種での頻出パターンと応用】
【頻出パターン1:RC回路の過渡現象】
・今回と同様の電流比・電圧比問題
・RC時定数を問う問題
・充電・放電曲線のグラフ問題
【頻出パターン2:RL回路の過渡現象】
・コイルの場合:最初「開放」、最後「短絡」
・RL時定数:\( \tau = \frac{L}{R} \)
・電流の立ち上がり特性
【頻出パターン3:RLC回路の過渡現象】
・減衰振動の概念
・臨界減衰・過減衰・不足減衰
・固有周波数と減衰定数
【頻出パターン4:実用的な応用問題】
・電力系統の開閉サージ
・モーターの始動特性
・電子回路のスイッチング特性
【解法の共通テクニック】
1. 過渡状態と定常状態の等価回路を描く
2. 初期条件を正確に把握する
3. 合成抵抗比から電流比を求める
4. 時定数を使った時間応答の計算
完璧や!ここまで理解できたら、過渡現象の問題はもう怖くないやろ?
最後に今日学んだことをまとめて、次の学習ステップも示しとくわ。これで電験三種の過渡現象分野がまた一歩前進やな!
【今日の学習成果と次のステップ】
【本日のポイント総復習】
1. コンデンサの過渡特性:最初「短絡」、最後「開放」
2. 等価回路法:過渡状態と定常状態で異なる回路として解析
3. 効率的解法:抵抗比の逆数が電流比
4. 物理的理解:コンデンサの充電過程と電流変化
5. 実用応用:突入電流、ソフトスタート、タイマー回路
【次の学習ステップ】
・RL回路の過渡現象(コイルの特性)
・RC時定数と指数関数的変化
・微分方程式による厳密解
・RLC回路の減衰振動
・ラプラス変換を使った解法
【継続学習のコツ】
・「最初と最後」の状態を必ず確認する
・等価回路を正確に描く習慣をつける
・実際の回路での過渡現象を意識する
・時定数の物理的意味を理解する
【重要な覚え方】
・コンデンサ:「ショート → オープン」
・コイル:「オープン → ショート」
お疲れさまでした!過渡現象をマスターして、電験三種合格に向けて着実に前進しましょう!
解説まとめ
問題回路図

■ RC回路の過渡現象とは
過渡現象とは、回路に電源を投入した瞬間から定常状態に至るまでの変化過程のことです。RC回路では、コンデンサの充電特性により電流が時間とともに変化します。この現象の理解は、電力系統の開閉サージや制御回路の応答特性を解析する上で極めて重要な基礎知識となります。
■ 計算手順と公式
コンデンサの過渡状態と定常状態
コンデンサの動作は時間経過とともに大きく変化します。
過渡状態(t = 0):コンデンサは短絡状態
定常状態(t → ∞):コンデンサは開放状態
リアクトル(コイル)の過渡状態と定常状態
リアクトルは電流変化を嫌う性質があります。
過渡状態(t = 0):リアクトルは開放状態
定常状態(t → ∞):リアクトルは短絡状態
合成抵抗の計算
直列接続と並列接続の合成抵抗を求める公式を適用します。
直列:\( R = R_1 + R_2 \)
並列:\( R = \frac{R_1 R_2}{R_1 + R_2} \)
オームの法則の適用
各状態における電流を求めるためにオームの法則を使用します。
\( I = \frac{V}{R} \ \mathrm{[A]} \)
■ 具体的な計算例
問題条件
6Ω、4Ω、12Ωの抵抗とコンデンサからなる回路において、スイッチS投入瞬間(t=0)と定常状態(t→∞)の点Aを流れる電流を求め、その比を計算します。コンデンサの初期電荷は零とします。
過渡状態(t = 0)の解析
コンデンサ短絡状態

Step 1: 回路の等価変換
コンデンサが短絡状態なので、4Ωと12Ωの抵抗が並列接続されます。
Step 2: 並列抵抗の計算
\[ \begin{aligned} R_{並列} &= \frac{4 \times 12}{4 + 12} \\[5pt] &= \frac{48}{16} \\[5pt] &= 3 \ \mathrm{[\Omega]} \end{aligned} \]Step 3: 過渡状態の合成抵抗
\[ \begin{aligned} R_0 &= 6 + 3 \\[5pt] &= 9 \ \mathrm{[\Omega]} \end{aligned} \]Step 4: 過渡状態の電流
\[ \begin{aligned} I_0 &= \frac{E}{R_0} \\[5pt] &= \frac{E}{9} \ \mathrm{[A]} \end{aligned} \]定常状態(t → ∞)の解析
コンデンサ開放状態

Step 1: 回路の等価変換
コンデンサが開放状態なので、電流は12Ωの抵抗のみを通って流れます。
Step 2: 定常状態の合成抵抗
\[ \begin{aligned} R_∞ &= 6 + 12 \\[5pt] &= 18 \ \mathrm{[\Omega]} \end{aligned} \]Step 3: 定常状態の電流
\[ \begin{aligned} I_∞ &= \frac{E}{R_∞} \\[5pt] &= \frac{E}{18} \ \mathrm{[A]} \end{aligned} \]Step 5: 電流比の計算
\[ \begin{aligned} \frac{I_0}{I_∞} &= \frac{\frac{E}{9}}{\frac{E}{18}} \\[5pt] &= \frac{E}{9} \times \frac{18}{E} \\[5pt] &= \frac{18}{9} \\[5pt] &= 2.0 \end{aligned} \]抵抗比と電流比の関係
電圧が一定の場合、合成抵抗と電流は反比例の関係にあります:
\( \frac{I_0}{I_∞} = \frac{R_∞}{R_0} = \frac{18}{9} = 2.0 \)
計算結果の比較
| 状態 | 時刻 | コンデンサ | 合成抵抗 [Ω] | 電流 [A] |
|---|---|---|---|---|
| 過渡状態 | t = 0 | 短絡 | 9 | E/9 |
| 定常状態 | t → ∞ | 開放 | 18 | E/18 |
結論:電流比 \( \frac{I_0}{I_∞} = 2.0 \) 答え:(4)
■ 実務上の留意点
RC回路の過渡現象は、電力系統や制御回路において重要な現象です。特に開閉サージや保護装置の動作において深い理解が必要となります。
開閉サージ対策:変圧器やコンデンサバンクの投入時に発生する過渡電流は、保護装置の誤動作や機器損傷の原因となるため、適切な限流対策が必要です。制御回路の応答特性:制御系の時定数はRC回路の時定数(τ = RC)で決まるため、応答速度と安定性のバランスを考慮した設計が重要です。保護継電器の設定:過渡電流による保護装置の不要動作を防ぐため、適切な時間設定や電流設定値の選定が必要です。
コンデンサバンクの運用:力率改善用コンデンサの投入時には大きな突入電流が流れるため、段階投入や限流リアクトルの設置を検討します。UPS・インバータ:平滑コンデンサの充電特性を考慮して、ソフトスタート機能や突入電流制限回路を設ける必要があります。絶縁協調:過渡現象時の電圧・電流は定常時より大きくなる場合があるため、機器の絶縁レベルは過渡時の値を考慮して決定します。測定精度:過渡現象は短時間で変化するため、高速応答の測定器や適切なサンプリング周波数での測定が重要です。