【理論】令和6年 (下期) 問1|異種誘電体を挿入した平行平板コンデンサにおける電荷に関する計算問題
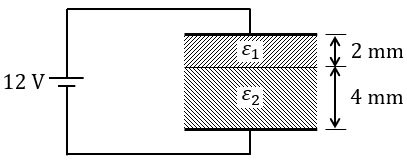
図のように,電極面積 \( 0.1 \) [m2],電極間隔 \( 6 \) [mm] の平行平板コンデンサに,
比誘電率 \( \varepsilon_1 = 2 \),厚さ \( 2 \) [mm] および 比誘電率 \( \varepsilon_2 = 4 \),厚さ \( 4 \) [mm] の 2 種類の誘電体が電極と平行に挿入されている。
このコンデンサに \( 12 \) [V] の直流電圧を印加したとき,蓄えられる電荷の値 \( [\mathrm{C}] \) として,最も近いものを次の (1)~(5) のうちから一つ選べ。
ただし,真空の誘電率 \( \varepsilon_0 = 8.85 \times 10^{-12} \) [F/m] とし,コンデンサの端効果は無視するものとする。
合格への方程式
コンデンサの基本原理
コンデンサとは何か?
コンデンサ(キャパシタ)は、電気エネルギーを蓄える電子部品です。身近な例で言うと、水を溜めるタンクのような役割を果たします。水タンクが水を蓄えるように、コンデンサは電荷(電気)を蓄えることができます。
コンデンサの構造
コンデンサは基本的に以下の構造を持ちます:
- 導体板(電極):2枚の金属板
- 絶縁体(誘電体):電極の間に挟まれた材料
- 端子:外部回路との接続部分
静電容量の基本式
コンデンサの静電容量(キャパシタンス)Cは、どれだけ多くの電荷を蓄えられるかを表す値です。
\[ Q = CV \]ここで:
- \( Q \):蓄えられる電荷 \( [\mathrm{C}] \)
- \( C \):静電容量 \( [\mathrm{F}] \)
- \( V \):印加電圧 \( [\mathrm{V}] \)
単位について
静電容量の単位はファラッド(F)です。実際の回路では非常に小さな値を扱うため、以下の単位がよく使われます:
- マイクロファラッド:\( \mu\mathrm{F} = 10^{-6} \mathrm{F} \)
- ナノファラッド:\( \mathrm{nF} = 10^{-9} \mathrm{F} \)
- ピコファラッド:\( \mathrm{pF} = 10^{-12} \mathrm{F} \)
平行平板コンデンサの静電容量
最も基本的な平行平板コンデンサの静電容量は以下の式で表されます:
\[ C = \frac{\varepsilon_0 S}{d} \]ここで:
- \( \varepsilon_0 \):真空の誘電率 \( = 8.85 \times 10^{-12} \, [\mathrm{F/m}] \)
- \( S \):電極の面積 \( [\mathrm{m^2}] \)
- \( d \):電極間の距離 \( [\mathrm{m}] \)
身近な例で理解しよう
静電容量の式を水タンクで例えると:
- 面積 S が大きい → タンクの底面積が大きい → より多くの水(電荷)が入る
- 距離 d が小さい → タンクの高さが低い → 同じ水量でも水位(電圧)が低くなる
コンデンサの基本的な性質
1. 電荷の蓄積
コンデンサは電荷を蓄えることができます。一方の電極に正の電荷が蓄積されると、もう一方の電極には同じ量の負の電荷が蓄積されます。
2. 電場の形成
電極間には電場が形成されます。この電場の強さは以下の式で表されます:
\[ E = \frac{V}{d} \]ここで \( E \) は電場の強さ \( [\mathrm{V/m}] \) です。
3. エネルギーの蓄積
コンデンサに蓄えられるエネルギー \( W \) は以下の式で計算できます:
\[ W = \frac{1}{2}CV^2 = \frac{1}{2}QV = \frac{Q^2}{2C} \]注意点
コンデンサは直流では電流を通しませんが、交流では周波数に応じて電流を通します。これは充放電による見かけ上の電流です。
誘電体と誘電率
誘電体とは何か?
誘電体とは、電気を通さない絶縁体のことです。身近な例では、プラスチック、ガラス、セラミック、空気なども誘電体です。コンデンサでは、この誘電体を電極間に挟むことで性能を向上させます。
誘電体の役割
- 絶縁:電極間の短絡を防ぐ
- 静電容量の増加:コンデンサの容量を大きくする
- 耐電圧の向上:より高い電圧に耐えられる
誘電率の概念
絶対誘電率 ε
絶対誘電率は、その材料の電場に対する応答の強さを表します。真空の誘電率 \( \varepsilon_0 \) を基準として考えます。
\[ \varepsilon_0 = 8.85 \times 10^{-12} \, [\mathrm{F/m}] \]比誘電率 εr
比誘電率は、真空に対してその材料がどれだけ静電容量を増加させるかを表す無次元の数値です。
\[ \varepsilon_r = \frac{\varepsilon}{\varepsilon_0} \]したがって、絶対誘電率は:
\[ \varepsilon = \varepsilon_r \varepsilon_0 \]主な材料の比誘電率
| 材料 | 比誘電率 εr | 特徴・用途 |
|---|---|---|
| 真空・空気 | 1.0 | 基準値 |
| ポリエチレン | 2.3 | 高周波用、低損失 |
| マイカ | 5〜7 | 高精度、高安定性 |
| アルミナ(Al₂O₃) | 9〜10 | 高温用セラミック |
| チタン酸バリウム | 1000〜10000 | 高容量セラミック |
| 水 | 81 | 液体誘電体 |
誘電体を挿入したコンデンサ
平行平板コンデンサに誘電体を挿入すると、静電容量は比誘電率倍になります:
\[ C = \frac{\varepsilon_r \varepsilon_0 S}{d} \]計算例
面積 \( 0.01 \, \mathrm{m^2} \)、間隔 \( 1 \, \mathrm{mm} \) の平行平板コンデンサを考えます:
- 真空の場合:\( C = \frac{8.85 \times 10^{-12} \times 0.01}{1 \times 10^{-3}} = 8.85 \times 10^{-11} \, \mathrm{F} \)
- 比誘電率4の誘電体を挿入:\( C = 4 \times 8.85 \times 10^{-11} = 3.54 \times 10^{-10} \, \mathrm{F} \)
つまり、静電容量が4倍になります!
誘電体中の電場
誘電体を挿入すると、電場の強さも変化します:
\[ E = \frac{E_0}{\varepsilon_r} \]ここで \( E_0 \) は真空中の電場の強さです。つまり、誘電体を挿入すると電場は弱くなります。
分極現象
誘電体に電場を加えると、分極という現象が起こります:
分極のメカニズム
- 電子分極:原子内の電子雲が変形
- イオン分極:イオン結晶で正負イオンが相対的に移動
- 配向分極:極性分子が電場方向に配向
この分極により、誘電体表面に電荷が現れ、外部電場を打ち消す内部電場が生じます。これが誘電体効果の本質です。
絶縁破壊について
誘電体には絶縁破壊電圧があります。これを超える電圧を加えると、誘電体が破壊され、導体になってしまいます。実用的なコンデンサでは、この値の1/2〜1/3程度の電圧で使用します。
複合誘電体の計算
複合誘電体コンデンサとは
複合誘電体コンデンサとは、複数の異なる誘電体を組み合わせたコンデンサです。実際の工業製品では、性能向上や製造コスト削減のために、異なる特性を持つ誘電体を組み合わせることがよくあります。
複合誘電体の配置方法
- 直列配置:電場方向に異なる誘電体を重ねる(本問題のタイプ)
- 並列配置:電場に垂直方向に異なる誘電体を配置
直列配置の複合誘電体(重要)
問題図のように、電極間に異なる誘電体が電場方向に重なって配置されている場合を考えます。
基本的な考え方
直列配置では、各誘電体部分を個別のコンデンサとして扱い、それらが直列接続されていると考えます。
なぜ直列接続?
電場方向に重なった誘電体では:
- 各部分に同じ電荷が蓄積される
- 各部分の電圧が加算される
- これは直列接続の特徴そのものです
各部分の静電容量計算
誘電体1(比誘電率 \( \varepsilon_{r1} \)、厚さ \( d_1 \))の静電容量:
\[ C_1 = \frac{\varepsilon_{r1} \varepsilon_0 S}{d_1} \]誘電体2(比誘電率 \( \varepsilon_{r2} \)、厚さ \( d_2 \))の静電容量:
\[ C_2 = \frac{\varepsilon_{r2} \varepsilon_0 S}{d_2} \]合成静電容量の計算
直列接続の合成静電容量は:
\[ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} \]したがって:
\[ \begin{aligned} C &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &= \frac{\frac{\varepsilon_{r1} \varepsilon_0 S}{d_1} \cdot \frac{\varepsilon_{r2} \varepsilon_0 S}{d_2}}{\frac{\varepsilon_{r1} \varepsilon_0 S}{d_1} + \frac{\varepsilon_{r2} \varepsilon_0 S}{d_2}} \\[10pt] &= \frac{\varepsilon_0 S}{\frac{d_1}{\varepsilon_{r1}} + \frac{d_2}{\varepsilon_{r2}}} \end{aligned} \]一般式の導出(重要)
n個の誘電体が直列に配置された場合の一般式:
\[ C = \frac{\varepsilon_0 S}{\frac{d_1}{\varepsilon_{r1}} + \frac{d_2}{\varepsilon_{r2}} + \frac{d_3}{\varepsilon_{r3}} + \cdots} \]この式は電験でよく使われるので、必ず覚えておきましょう。
並列配置の複合誘電体
電場に垂直方向に異なる誘電体が配置されている場合、各部分は並列接続となります。
並列配置の特徴
- 各部分に同じ電圧が印加される
- 各部分の電荷が加算される
合成静電容量
面積が \( S_1, S_2 \) の部分に分かれている場合:
\[ C = C_1 + C_2 = \frac{\varepsilon_{r1} \varepsilon_0 S_1}{d} + \frac{\varepsilon_{r2} \varepsilon_0 S_2}{d} \]電場と電圧の分布
直列配置の複合誘電体では、各部分の電場と電圧の分布を理解することが重要です。
電場の分布
各誘電体中の電場の強さは:
\[ E_1 = \frac{D}{\varepsilon_{r1} \varepsilon_0}, \quad E_2 = \frac{D}{\varepsilon_{r2} \varepsilon_0} \]ここで \( D \) は電束密度(各部分で同じ値)です。
電圧の分布
各誘電体部分の電圧は:
\[ V_1 = E_1 d_1, \quad V_2 = E_2 d_2 \]全体の印加電圧は:
\[ V = V_1 + V_2 \]設計上の注意点
複合誘電体では、各部分の電場の強さが異なるため、絶縁破壊が起こりやすい部分を特定して設計する必要があります。一般に、比誘電率が小さい材料ほど電場が強くなり、破壊しやすくなります。
実用的な応用例
複合誘電体コンデンサの応用
- 高圧コンデンサ:異なる耐電圧の材料を組み合わせ
- 温度補償コンデンサ:温度特性の異なる材料を組み合わせ
- 多層セラミックコンデンサ:製造工程で異なる特性を持つ層が形成
- 電力用コンデンサ:コスト削減のために安価な材料を組み合わせ
これらの応用により、単一誘電体では実現できない特性を持つコンデンサが製造されています。
実践問題の解法
問題の分析手順
複合誘電体コンデンサの問題を解く際の標準的な手順を身につけましょう。
解法の基本ステップ
- 問題図の理解:誘電体の配置を正確に把握
- 各部分の静電容量計算:個別のコンデンサとして計算
- 接続方法の判定:直列か並列かを判断
- 合成静電容量の計算:適切な公式を適用
- 電荷の計算:Q = CV を使用
- 答えの確認:単位や桁数の妥当性をチェック
本問題の詳細解法
ステップ1:問題の理解
与えられた条件を整理します:
- 電極面積:\( S = 0.1 \, \mathrm{m^2} \)
- 全体の電極間隔:\( d_{total} = 6 \, \mathrm{mm} = 6 \times 10^{-3} \, \mathrm{m} \)
- 誘電体1:\( \varepsilon_{r1} = 2 \)、\( d_1 = 2 \, \mathrm{mm} = 2 \times 10^{-3} \, \mathrm{m} \)
- 誘電体2:\( \varepsilon_{r2} = 4 \)、\( d_2 = 4 \, \mathrm{mm} = 4 \times 10^{-3} \, \mathrm{m} \)
- 印加電圧:\( V = 12 \, \mathrm{V} \)
- 真空の誘電率:\( \varepsilon_0 = 8.85 \times 10^{-12} \, \mathrm{F/m} \)
確認
\( d_1 + d_2 = 2 + 4 = 6 \, \mathrm{mm} = d_{total} \) ✓
ステップ2:各部分の静電容量計算
誘電体1の静電容量:
\[ \begin{aligned} C_1 &= \frac{\varepsilon_{r1} \varepsilon_0 S}{d_1} \\[10pt] &= \frac{2 \times 8.85 \times 10^{-12} \times 0.1}{2 \times 10^{-3}} \\[10pt] &= \frac{1.77 \times 10^{-12}}{2 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-10} \, \mathrm{F} \end{aligned} \]誘電体2の静電容量:
\[ \begin{aligned} C_2 &= \frac{\varepsilon_{r2} \varepsilon_0 S}{d_2} \\[10pt] &= \frac{4 \times 8.85 \times 10^{-12} \times 0.1}{4 \times 10^{-3}} \\[10pt] &= \frac{3.54 \times 10^{-12}}{4 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-10} \, \mathrm{F} \end{aligned} \]興味深い結果
\( C_1 = C_2 \) となりました!これは偶然ではなく、以下の関係があるためです:
\[ \frac{\varepsilon_{r1}}{d_1} = \frac{2}{2} = 1, \quad \frac{\varepsilon_{r2}}{d_2} = \frac{4}{4} = 1 \]つまり、「比誘電率/厚さ」の比が同じなので、静電容量も同じになります。
ステップ3:合成静電容量の計算
直列接続なので:
\[ C = \frac{C_1 C_2}{C_1 + C_2} \]\( C_1 = C_2 \) の場合:
\[ \begin{aligned} C &= \frac{C_1^2}{C_1 + C_1} = \frac{C_1^2}{2C_1} = \frac{C_1}{2} \\[10pt] &= \frac{8.85 \times 10^{-10}}{2} \\[10pt] &= 4.425 \times 10^{-10} \, \mathrm{F} \end{aligned} \]ステップ4:蓄積電荷の計算
最終的に求める電荷:
\[ \begin{aligned} Q &= CV \\[10pt] &= 4.425 \times 10^{-10} \times 12 \\[10pt] &= 5.31 \times 10^{-9} \, \mathrm{C} \end{aligned} \]答えの確認
計算結果 \( 5.31 \times 10^{-9} \, \mathrm{C} \) は選択肢(1) \( 5.3 \times 10^{-9} \) に最も近い値です。
計算のポイントと注意事項
1. 単位の統一
計算前に必ず単位を統一しましょう:
- 長さ:すべて [m] に統一(mm → m の変換)
- 面積:[m²] で統一
- 誘電率:[F/m] で統一
よくある間違い
- 単位変換ミス:mm を m に変換し忘れ
- 接続方法の誤認:直列と並列を間違える
- 面積の取り扱い:各部分で面積が同じことを見落とす
2. 計算の検算方法
以下の方法で検算できます:
検算方法1:一般式を使用
\[ C = \frac{\varepsilon_0 S}{\frac{d_1}{\varepsilon_{r1}} + \frac{d_2}{\varepsilon_{r2}}} \] \[ \begin{aligned} C &= \frac{8.85 \times 10^{-12} \times 0.1}{\frac{2 \times 10^{-3}}{2} + \frac{4 \times 10^{-3}}{4}} \\[10pt] &= \frac{8.85 \times 10^{-13}}{1 \times 10^{-3} + 1 \times 10^{-3}} \\[10pt] &= \frac{8.85 \times 10^{-13}}{2 \times 10^{-3}} \\[10pt] &= 4.425 \times 10^{-10} \, \mathrm{F} \end{aligned} \]同じ結果が得られます ✓
類似問題の解法パターン
パターン1:3つ以上の誘電体
誘電体がn個ある場合の一般的解法:
\[ \frac{1}{C} = \sum_{i=1}^{n} \frac{1}{C_i} = \sum_{i=1}^{n} \frac{d_i}{\varepsilon_{ri} \varepsilon_0 S} \]パターン2:異なる面積を持つ場合
各誘電体部分の面積が異なる場合は、個別に面積を考慮して計算します。
パターン3:並列配置との組み合わせ
直列と並列が混在する場合は、段階的に合成静電容量を求めます。
実験的理解を深める
実際の測定での注意点
- 端効果:実際のコンデンサでは電極端部で電場が不均一になる
- 温度依存性:誘電率は温度により変化する
- 周波数依存性:交流測定では周波数により静電容量が変化
- 湿度の影響:空気の誘電率は湿度により変化
発展的な考察
エネルギー密度の分布
各誘電体中のエネルギー密度は異なります:
\[ u = \frac{1}{2} \varepsilon E^2 \]電場が強い部分(比誘電率が小さい部分)により多くのエネルギーが蓄積されます。
温度特性の設計
実用的なコンデンサでは、温度による静電容量変化を最小化するため、温度係数の異なる誘電体を組み合わせることがあります。
応用例:温度補償
誘電体Aの温度係数が+100 ppm/℃、誘電体Bの温度係数が-50 ppm/℃の場合、適切な比率で組み合わせることで温度特性を改善できます。
問題演習のヒント
効率的な学習方法
- 基本公式の暗記:\( C = \frac{\varepsilon_r \varepsilon_0 S}{d} \) は必須
- 直列・並列の判別練習:図を見て瞬時に判断できるまで練習
- 計算ミスの防止:単位変換と桁数の確認を習慣化
- 類似問題の反復:パターンを身体で覚える
- 物理的イメージ:式の背景にある物理現象を理解
時間短縮のテクニック
試験では時間が限られているため、以下のテクニックが有効です:
- 対称性の利用:本問のように \( C_1 = C_2 \) の場合、\( C = C_1/2 \) と簡単に計算
- 近似計算:最終段階で適切に四捨五入
- 選択肢の活用:大まかな計算で選択肢を絞り込む
最終確認事項
答えを出した後、必ず以下を確認しましょう:
- 単位は正しいか?(電荷なので [C])
- 桁数は妥当か?(ナノクーロンオーダー)
- 物理的に妥当か?(より大きな誘電率なら、より多くの電荷)
🔍 ワンポイントアドバイス: 複合誘電体の問題では、まず「各部分を個別のコンデンサとして扱う」という基本的な考え方を身につけることが最も重要です。直列・並列の判別ができれば、あとは基本的な静電容量の公式と合成の公式を適用するだけです。計算ミスを防ぐため、単位変換と桁数の確認を必ず行いましょう。
よっしゃ!今回は平行平板コンデンサに2種類の誘電体が挿入された問題やな。まず、この問題を解くために何を求めなあかんか分かるか?
はい、先生。電荷 \(Q\) を求める問題ですから、\(Q = CV\) の関係式を使って、まずはコンデンサ全体の静電容量 \(C\) を求める必要がありますね。
与えられた条件を整理すると:
・電極面積:\(S = 0.1 \, \mathrm{m^2}\)
・電極間隔:全体で \(6 \, \mathrm{mm}\)(誘電体1が \(2 \, \mathrm{mm}\)、誘電体2が \(4 \, \mathrm{mm}\))
・誘電体1:比誘電率 \(\varepsilon_1 = 2\)、厚さ \(d_1 = 2 \, \mathrm{mm}\)
・誘電体2:比誘電率 \(\varepsilon_2 = 4\)、厚さ \(d_2 = 4 \, \mathrm{mm}\)
・印加電圧:\(V = 12 \, \mathrm{V}\)
その通りや!条件整理もバッチリやな。ところで、この2つの誘電体はどんな接続になってるか分かるか?図をよう見てみ。これが分からんと合成静電容量の計算方法が決まらへんからな。
はい、図を見ると2つの誘電体が電極と平行に配置されているので、電流の流れを考えると直列接続になりますね。
つまり、電圧は各誘電体に分かれて加わりますが、電荷は同じ値になります。これは直列回路の特徴ですね。
直列接続の場合、合成静電容量は:
\(\displaystyle \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}\)
または
\(\displaystyle C = \frac{C_1 C_2}{C_1 + C_2}\)
の公式を使います。
完璧や!直列接続の理解もバッチリやな。せやったら、まずは各誘電体部分の静電容量 \(C_1\) と \(C_2\) を計算してみよか。平行平板コンデンサの静電容量の公式、覚えてるか?
はい、平行平板コンデンサの静電容量は:
\(\displaystyle C = \frac{\varepsilon_r \varepsilon_0 S}{d}\)
ですね。ここで、\(\varepsilon_r\) は比誘電率、\(\varepsilon_0\) は真空の誘電率、\(S\) は電極面積、\(d\) は電極間距離です。
それでは \(C_1\) から計算します:
\[ \begin{aligned} C_1 &= \frac{\varepsilon_1 \varepsilon_0 S}{d_1} \\[10pt] &= \frac{2 \times 8.85 \times 10^{-12} \times 0.1}{2 \times 10^{-3}} \\[10pt] &= \frac{1.77 \times 10^{-12}}{2 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-10} \, \mathrm{[F]} \end{aligned} \]ええぞ!\(C_1\) の計算も正確やな。今度は \(C_2\) を計算してみよか。ちなみに、計算してみたら面白い結果になるで〜。どんな結果になるか予想してみ?
はい、\(C_2\) を計算してみます:
\[ \begin{aligned} C_2 &= \frac{\varepsilon_2 \varepsilon_0 S}{d_2} \\[10pt] &= \frac{4 \times 8.85 \times 10^{-12} \times 0.1}{4 \times 10^{-3}} \\[10pt] &= \frac{3.54 \times 10^{-12}}{4 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-10} \, \mathrm{[F]} \end{aligned} \]あ!先生、\(C_1 = C_2 = 8.85 \times 10^{-10} \, \mathrm{[F]}\) になりました!
これは偶然ではなくて、誘電体1は比誘電率が小さいけれど厚さも薄く、誘電体2は比誘電率が大きいけれど厚さも厚いので、結果的に同じ静電容量になったのですね。
その通り!よう気づいたな〜。これは電験でよくある「計算を簡単にするための数値設定」なんや。\(C_1 = C_2\) になったから、直列合成の計算がめっちゃ楽になるで。直列で同じ静電容量のコンデンサが2個つながったら、合成静電容量はどうなるか分かるか?
はい!同じ静電容量 \(C_1 = C_2\) のコンデンサが直列接続された場合:
\[ \begin{aligned} C &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &= \frac{C_1 \times C_1}{C_1 + C_1} \\[10pt] &= \frac{C_1^2}{2C_1} \\[10pt] &= \frac{C_1}{2} \end{aligned} \]つまり、同じ静電容量のコンデンサを直列接続すると、合成静電容量は元の半分になります。
したがって:
\[ \begin{aligned} C &= \frac{C_1}{2} \\[10pt] &= \frac{8.85 \times 10^{-10}}{2} \\[10pt] &= 4.425 \times 10^{-10} \, \mathrm{[F]} \end{aligned} \]完璧や!合成静電容量も正確に求められたな。最後に電荷 \(Q\) を計算してみよか。\(Q = CV\) の公式を使って、答えを出してみ!
はい、最後に電荷を計算します:
\[ \begin{aligned} Q &= CV \\[10pt] &= 4.425 \times 10^{-10} \times 12 \\[10pt] &= 5.31 \times 10^{-9} \, \mathrm{[C]} \end{aligned} \]選択肢を見ると、(1) \(5.3 \times 10^{-9}\) が最も近い値ですね。
答え:(1) \(5.3 \times 10^{-9}\)
よっしゃ!完璧に解けたな〜。最後に、この問題のポイントと、実際の現場でどう使われるかも教えとこか。誘電体の直列接続って、実は身近なところでも使われてるんやで。
ありがとうございます!この問題を通して学んだポイントをまとめさせていただきます:
【解法のポイント】
1. 誘電体が電極と平行に配置されている場合は直列接続
2. 各誘電体部分の静電容量を個別に計算
3. 直列合成公式で全体の静電容量を求める
4. \(Q = CV\) で電荷を計算
【つまずきやすいポイント】
・誘電体の配置から直列か並列かを正しく判断する
・各誘電体の厚さを正しく単位変換する(mm → m)
・計算過程で桁数を間違えないよう注意する
【実用例】
・電力用コンデンサの絶縁設計
・スマートフォンの液晶パネル(複数の絶縁層)
・高電圧機器の絶縁協調設計
このような複合誘電体は、各層の電界強度を制御して絶縁破壊を防ぐ重要な技術なんですね。
解説まとめ
■ 複合誘電体コンデンサとは
複合誘電体コンデンサは、複数の異なる誘電体材料を組み合わせたコンデンサです。各誘電体の比誘電率と厚さによって、コンデンサ全体の特性が決まります。この問題では、2種類の誘電体が電極と平行に配置されているため、電気的には直列接続となります。各誘電体部分をそれぞれ1つのコンデンサとして扱い、直列合成静電容量を求めることで、コンデンサ全体の特性を計算できます。
■ 計算手順と公式
- 平行平板コンデンサの静電容量
誘電体を挿入した平行平板コンデンサの静電容量は次式で求められます。
\( C = \frac{\varepsilon_r \varepsilon_0 S}{d} \)
ここで、Cは静電容量[F]、εrは比誘電率、ε0は真空の誘電率[F/m]、Sは電極面積[m²]、dは誘電体の厚さ[m]です。
- 直列接続コンデンサの合成静電容量
直列接続されたコンデンサの合成静電容量は次式で計算されます。
\( C = \frac{C_1 C_2}{C_1 + C_2} \)
2つのコンデンサが同じ静電容量の場合:\( C = \frac{C_1}{2} \)
- 電荷と静電容量の関係
コンデンサに蓄えられる電荷は静電容量と電圧の積で求められます。
\( Q = CV \)
ここで、Qは電荷[C]、Vは印加電圧[V]です。
■ 具体的な計算例
問題条件
- 電極面積: \( S = 0.1 \ \mathrm{[m^2]} \)
- 電極間隔: 6 mm(誘電体1: 2mm、誘電体2: 4mm)
- 誘電体1: \( \varepsilon_1 = 2 \)、厚さ \( d_1 = 2 \ \mathrm{[mm]} = 2 \times 10^{-3} \ \mathrm{[m]} \)
- 誘電体2: \( \varepsilon_2 = 4 \)、厚さ \( d_2 = 4 \ \mathrm{[mm]} = 4 \times 10^{-3} \ \mathrm{[m]} \)
- 印加電圧: \( V = 12 \ \mathrm{[V]} \)
- 真空の誘電率: \( \varepsilon_0 = 8.85 \times 10^{-12} \ \mathrm{[F/m]} \)
各誘電体部分の静電容量計算
誘電体1の静電容量:
\[ \begin{aligned} C_1 &= \frac{\varepsilon_1 \varepsilon_0 S}{d_1} \\[5pt] &= \frac{2 \times 8.85 \times 10^{-12} \times 0.1}{2 \times 10^{-3}} \\[5pt] &= \frac{1.77 \times 10^{-12}}{2 \times 10^{-3}} \\[5pt] &= 8.85 \times 10^{-10} \ \mathrm{[F]} \end{aligned} \]誘電体2の静電容量:
\[ \begin{aligned} C_2 &= \frac{\varepsilon_2 \varepsilon_0 S}{d_2} \\[5pt] &= \frac{4 \times 8.85 \times 10^{-12} \times 0.1}{4 \times 10^{-3}} \\[5pt] &= \frac{3.54 \times 10^{-12}}{4 \times 10^{-3}} \\[5pt] &= 8.85 \times 10^{-10} \ \mathrm{[F]} \end{aligned} \]興味深いことに、\( C_1 = C_2 \) となります。
コンデンサ全体の静電容量計算
2つのコンデンサが直列接続されているため:
\[ \begin{aligned} C &= \frac{C_1 C_2}{C_1 + C_2} \\[5pt] &= \frac{C_1^2}{C_1 + C_1} \\[5pt] &= \frac{C_1}{2} \\[5pt] &= \frac{8.85 \times 10^{-10}}{2} \\[5pt] &= 4.425 \times 10^{-10} \ \mathrm{[F]} \end{aligned} \]蓄えられる電荷の計算
\[ \begin{aligned} Q &= CV \\[5pt] &= 4.425 \times 10^{-10} \times 12 \\[5pt] &= 5.31 \times 10^{-9} \ \mathrm{[C]} \end{aligned} \]結論:コンデンサに蓄えられる電荷は 5.31×10⁻⁹ [C] である。(解答:選択肢(1))
■ 実務上の留意点
複合誘電体コンデンサの設計と応用における実務上の留意点です。
- 複合誘電体では、各誘電体の絶縁破壊強度が異なるため、電界分布を考慮した設計が重要です。誘電率の小さい材料ほど高い電界が印加されます。
- 温度特性の異なる誘電体を組み合わせる場合、温度変化による静電容量の変動を考慮する必要があります。
- 実際の製品では、誘電体間の界面での部分放電や層間剥離などの劣化現象に注意が必要です。
- 高電圧用途では、各誘電体層の厚さと絶縁破壊強度のバランスを最適化することで、コンデンサの小型化と信頼性向上を両立できます。
- 電力用コンデンサでは、誘電損失の小さい材料の選定と組み合わせが効率向上に重要です。
- 製造時の気泡や異物混入は電界集中の原因となるため、品質管理が重要です。