【理論】令和3年 問1|「異種誘電体を含む平行板コンデンサにおける電束と電気力線の分布に関する穴埋め問題
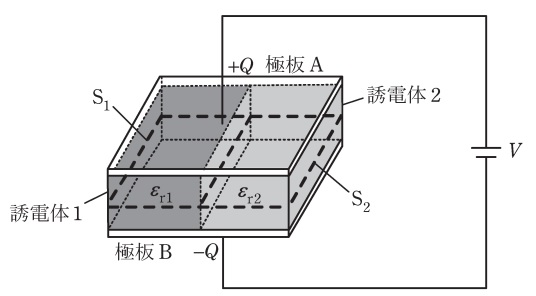
図のように,同じ寸法の直方体で誘電率の異なる二つの誘電体(比誘電率 \( \varepsilon_{\mathrm{r1}} \) の誘電体 \( 1 \) と比誘電率 \( \varepsilon_{\mathrm{r2}} \) の誘電体 \( 2 \))が平行板コンデンサに充填されている。
極板間は一定の電圧 \( V \) [V] に保たれ,極板 \( \mathrm{A} \) と極板 \( \mathrm{B} \) にはそれぞれ \( +Q \) [C] と \( -Q \) [C](\( Q > 0 \))の電荷が蓄えられている。
誘電体 \( 1 \) と誘電体 \( 2 \) は平面で接しており,その境界面は極板に対して垂直である。ただし,端効果は無視できるものとする。
この平行板コンデンサにおいて,極板 \( \mathrm{A} \),\( \mathrm{B} \) に平行な誘電体 \( 1 \),誘電体 \( 2 \) の断面をそれぞれ面 \( \mathrm{S_1} \),面 \( \mathrm{S_2} \)(面 \( \mathrm{S_1} \) と面 \( \mathrm{S_2} \) の断面積は等しい)とすると,
面 \( \mathrm{S_1} \) を貫く電気力線の総数(任意の点の電気力線の密度は,その点での電界の大きさを表す)は,面 \( \mathrm{S_2} \) を貫く電気力線の総数の \( \fbox{(ア)} \) 倍である。
面 \( \mathrm{S_1} \) を貫く電束の総数は面 \( \mathrm{S_2} \) を貫く電束の総数の \( \fbox{(イ)} \) 倍であり,
面 \( \mathrm{S_1} \) と面 \( \mathrm{S_2} \) を貫く電束の数の総和は \( \fbox{(ウ)} \) である。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,正しいものを次の (1)~(5) のうちから一つ選べ。
\begin{array}{cccc} & (ア) & (イ) & (ウ) \\ \hline (1) & 1 & \displaystyle \frac {\varepsilon _{\mathrm {r1}}}{\varepsilon _{\mathrm {r2}}} & Q \\ \hline (2) & 1 & \displaystyle \frac {\varepsilon _{\mathrm {r1}}}{\varepsilon _{\mathrm {r2}}} & \displaystyle \frac {Q}{\varepsilon _{\mathrm {r1}}}+\frac {Q}{\varepsilon _{\mathrm {r2}}} \\ \hline (3) & 1 & \displaystyle \frac {\varepsilon _{\mathrm {r2}}}{\varepsilon _{\mathrm {r1}}} & \displaystyle \frac {Q}{\varepsilon _{\mathrm {r1}}}+\frac {Q}{\varepsilon _{\mathrm {r2}}} \\ \hline (4) & \displaystyle \frac {\varepsilon _{\mathrm {r2}}}{\varepsilon _{\mathrm {r1}}} & 1 & \displaystyle \frac {Q}{\varepsilon _{\mathrm {r1}}}+\frac {Q}{\varepsilon _{\mathrm {r2}}} \\ \hline (5) & \displaystyle \frac {\varepsilon _{\mathrm {r2}}}{\varepsilon _{\mathrm {r1}}} & 1 & Q \\ \hline \end{array}
合格への方程式
電気力線の特徴
電気力線は電界を可視化するための概念で、正電荷から負電荷に向かう仮想の線です。電気力線を理解することで、電界の様子を直感的に把握することができます。
電気力線の5つの基本特性
- 電気力線の本数は電荷\(Q \; [\mathrm{C}]\)と誘電率\(\varepsilon \; [\mathrm{F/m}]\)を用いると、\(\frac{Q}{\varepsilon}\)本である。
- 電気力線は正電荷から垂直に出て、負電荷に垂直に入る。
- 電気力線同士は反発し合う。
- 電気力線は枝分かれしたり、交差したりしない。
- 電気力線の向きは電界の向きと一致し、電気力線の密度は電界の大きさに比例する。
電気力線と電荷の関係
電気力線の本数は電荷量に比例します。電荷\(Q\)から出る電気力線の本数\(N\)は次のように表されます:
\[ \begin{aligned} N = \frac{Q}{\varepsilon} \\[10pt] \end{aligned} \]
ここで、\(\varepsilon\)は媒質の誘電率です。真空中では\(\varepsilon_0 = 8.85 \times 10^{-12} \; [\mathrm{F/m}]\)となります。
電気力線の密度と電界の強さ
単位面積あたりの電気力線の本数(密度)は、その点における電界の強さに比例します。これは電気力線の特性5に対応します。
\[ E = \frac{N}{S} = \frac{D}{\varepsilon} \\[10pt] \]
ここで、\(E \; [\mathrm{V/m}]\)は電界の強さ、\(N\)は面積\(S \; [\mathrm{m^2}]\)を通過する電気力線の本数、\(D \; [\mathrm{C/m^2}]\)は電束密度です。
代表的な電気力線の分布パターン
| 配置 | 電気力線の特徴 |
|---|---|
| 点電荷 | 放射状に広がる |
| 平行平板 | 平行で等間隔の直線 |
| 同符号の2つの点電荷 | 互いに反発し合うように湾曲 |
| 異符号の2つの点電荷 | 一方から他方へ向かって湾曲 |
実用上の注意点
電気力線は物理的に存在する実体ではなく、電界を可視化するための概念的なものです。実際の計算では、電界ベクトルや電位を用いた数学的な扱いが一般的です。
平行平板コンデンサの基本
平行平板コンデンサの構造
平行平板コンデンサは、最も基本的なコンデンサの形状で、2枚の導体平板(電極)が平行に配置された構造を持ちます。
基本構造と特性
- 2枚の平行な導体平板(電極)
- 平板間に誘電体(絶縁体)
- 平板の面積:\(S \; [\mathrm{m^2}]\)
- 平板間の距離:\(d \; [\mathrm{m}]\)
- 誘電体の誘電率:\(\varepsilon \; [\mathrm{F/m}]\)
電界と電圧の関係
極板間の距離\(d\)の平行平板コンデンサに電圧\(V\)をかけると、極板間に一様な電界\(E\)が発生します:
\[ \begin{aligned} E = \frac{V}{d} \; [\mathrm{V/m}] \\[10pt] \end{aligned} \]
電界の向き
電界の向きは、正極から負極に向かう方向です。つまり、高い電位から低い電位へ向かいます。平行平板コンデンサでは、電界は極板に垂直で、両極板間でほぼ一様です(端部の効果を無視した場合)。
平行平板コンデンサの静電容量
平行平板コンデンサの静電容量\(C\)は次のように表されます:
\[ \begin{aligned} C = \frac{\varepsilon S}{d} \; [\mathrm{F}] \\[10pt] \end{aligned} \]
ここで:
- \(\varepsilon\):誘電体の誘電率 \([\mathrm{F/m}]\)
- \(S\):極板の面積 \([\mathrm{m^2}]\)
- \(d\):極板間の距離 \([\mathrm{m}]\)
例題:平行平板コンデンサの電界計算
面積100cm²、間隔2mmの平行平板コンデンサに100Vの電圧を印加した場合の電界強度を求めよ。
解答:
与えられた値:
\(V = 100 \; [\mathrm{V}]\)
\(d = 2 \times 10^{-3} \; [\mathrm{m}]\)
電界強度の計算:
\[ \begin{aligned} E &= \frac{V}{d} \\[10pt] &= \frac{100}{2 \times 10^{-3}} \\[10pt] &= 5 \times 10^4 \; [\mathrm{V/m}] \\[10pt] &= 50 \; [\mathrm{kV/m}] \\[10pt] \end{aligned} \]
静電容量計算時の注意点
実際のコンデンサでは、端部効果(フリンジング効果)により電界が端部で歪むため、理論値と実測値に差が生じることがあります。精密な計算が必要な場合は、この効果を考慮する必要があります。
電界と電束密度
電束密度の定義
電束密度\(D\)は、単位面積あたりの電束の量を表し、電界\(E\)と誘電率\(\varepsilon\)を用いて次のように定義されます:
\[ \begin{aligned} D = \varepsilon E \; [\mathrm{C/m^2}] \\[10pt] \end{aligned} \]
電界と電束密度の関係
電界\(E\)は電位の勾配として定義され、力学的な作用を表します。一方、電束密度\(D\)は電荷の分布状態を表します。誘電体がない真空中では、\(D = \varepsilon_0 E\)となります。
ガウスの法則
ガウスの法則は、閉曲面を通過する電束の総量がその閉曲面内の電荷の総量に等しいという法則です:
\[ \begin{aligned} \oint_S \mathbf{D} \cdot d\mathbf{S} = Q_{\text{enclosed}} \\[10pt] \end{aligned} \]
ここで、\(Q_{\text{enclosed}}\)は閉曲面内の電荷の総量です。
平行平板コンデンサへの応用
平行平板コンデンサでは、ガウスの法則を用いると電束密度\(D\)は表面電荷密度\(\sigma\)に等しくなります:
\[ D = \sigma = \frac{Q}{S} \; [\mathrm{C/m^2}] \\[10pt] \]
ここで、\(Q\)は極板の電荷、\(S\)は極板の面積です。
電束密度と電荷の関係
コンデンサに蓄えられる電荷量\(Q\)と電束密度\(D\)、極板面積\(S\)の関係は次のようになります:
\[ \begin{aligned} Q &= D \cdot S \\[10pt] &= \varepsilon E \cdot S \\[10pt] &= \varepsilon \frac{V}{d} \cdot S \\[10pt] &= \frac{\varepsilon S}{d} \cdot V \\[10pt] &= C \cdot V \\[10pt] \end{aligned} \]
これは、コンデンサの基本式\(Q = CV\)に一致します。
例題:電束密度の計算
面積\(S = 200 \; \mathrm{cm^2}\)、間隔\(d = 0.5 \; \mathrm{mm}\)の平行平板コンデンサに\(V = 1000 \; \mathrm{V}\)の電圧を印加した。誘電体として比誘電率\(\varepsilon_r = 4\)の材料を使用した場合の電束密度\(D\)を求めよ。
解答:
与えられた値:
\(S = 200 \times 10^{-4} \; [\mathrm{m^2}]\)
\(d = 0.5 \times 10^{-3} \; [\mathrm{m}]\)
\(V = 1000 \; [\mathrm{V}]\)
\(\varepsilon_r = 4\)
\(\varepsilon = \varepsilon_r \varepsilon_0 = 4 \times 8.85 \times 10^{-12} \; [\mathrm{F/m}]\)
まず電界\(E\)を計算します:
\[ \begin{aligned} E &= \frac{V}{d} \\[10pt] &= \frac{1000}{0.5 \times 10^{-3}} \\[10pt] &= 2 \times 10^6 \; [\mathrm{V/m}] \\[10pt] \end{aligned} \]
次に電束密度\(D\)を計算します:
\[ \begin{aligned} D &= \varepsilon E \\[10pt] &= 4 \times 8.85 \times 10^{-12} \times 2 \times 10^6 \\[10pt] &= 7.08 \times 10^{-5} \; [\mathrm{C/m^2}] \\[10pt] &= 70.8 \; [\mu\mathrm{C/m^2}] \\[10pt] \end{aligned} \]
誘電体を挿入した場合
誘電体の基本特性
誘電体は電気を通さない絶縁体ですが、電界の中に置かれると分極現象を起こします。これにより、コンデンサの特性が変化します。
誘電体の主な効果
- 静電容量の増加(比誘電率\(\varepsilon_r\)倍)
- 蓄えられる電荷量の増加
- 耐電圧の向上
- 漏れ電流の低減
- コンデンサの小型化
比誘電率と誘電率
誘電体の特性は比誘電率\(\varepsilon_r\)で表されます。誘電率\(\varepsilon\)と真空の誘電率\(\varepsilon_0\)の関係は次のようになります:
\[ \begin{aligned} \varepsilon = \varepsilon_r \varepsilon_0 \\[10pt] \end{aligned} \]
ここで、\(\varepsilon_0 = 8.85 \times 10^{-12} \; [\mathrm{F/m}]\)は真空の誘電率です。
| 物質 | 比誘電率\(\varepsilon_r\) |
|---|---|
| 真空 | 1 |
| 空気 | 1.0006 |
| 紙 | 2〜4 |
| ガラス | 4〜10 |
| セラミック | 5〜10,000 |
| 水 | 80 |
誘電体を挿入したコンデンサの特性
誘電体を挿入した平行平板コンデンサの静電容量\(C\)は次のようになります:
\[ \begin{aligned} C = \varepsilon_r \varepsilon_0 \frac{S}{d} \; [\mathrm{F}] \\[10pt] \end{aligned} \]
誘電体挿入時の電界と電束密度
誘電体を挿入すると、電荷\(Q\)が一定の場合(充電後に誘電体を挿入する場合):
- 電束密度\(D\)は変化しない(\(D = \frac{Q}{S}\)のため)
- 電界\(E\)は\(\frac{1}{\varepsilon_r}\)倍に減少(\(E = \frac{D}{\varepsilon} = \frac{D}{\varepsilon_r \varepsilon_0}\))
- 電圧\(V\)も\(\frac{1}{\varepsilon_r}\)倍に減少(\(V = Ed\)より)
電圧\(V\)が一定の場合(電源に接続されている場合):
- 電界\(E\)は変化しない(\(E = \frac{V}{d}\)より)
- 電束密度\(D\)は\(\varepsilon_r\)倍に増加(\(D = \varepsilon E = \varepsilon_r \varepsilon_0 E\))
- 電荷\(Q\)も\(\varepsilon_r\)倍に増加(\(Q = DS = \varepsilon_r \varepsilon_0 ES\))
例題:誘電体挿入によるコンデンサの特性変化
空気中(\(\varepsilon_r = 1\))で\(C_0 = 50 \; \mathrm{pF}\)の静電容量を持つ平行平板コンデンサがある。この空隙に比誘電率\(\varepsilon_r = 5\)の誘電体を完全に挿入した場合、静電容量と電界の変化を求めよ。ただし、コンデンサは100Vの電源に接続されているものとする。
解答:
(1)誘電体挿入後の静電容量:
\[ \begin{aligned} C &= \varepsilon_r C_0 \\[10pt] &= 5 \times 50 \times 10^{-12} \\[10pt] &= 250 \times 10^{-12} \\[10pt] &= 250 \; [\mathrm{pF}] \\[10pt] \end{aligned} \]
(2)電界の変化:
電源に接続されているため、電圧\(V\)は一定(100V)です。よって電界\(E = \frac{V}{d}\)も変化しません。
(3)電荷の変化:
\[ \begin{aligned} Q_0 &= C_0 V = 50 \times 10^{-12} \times 100 = 5 \times 10^{-9} \; [\mathrm{C}] \\[10pt] Q &= C V = 250 \times 10^{-12} \times 100 = 25 \times 10^{-9} \; [\mathrm{C}] \\[10pt] \end{aligned} \]
したがって、電荷は5倍になります。
誘電体の制限
誘電体には耐電圧の限界があり、その限界を超えると絶縁破壊が起こります。これを誘電体の「絶縁破壊電界強度」または「誘電強度」といい、単位は[V/m]で表されます。設計時にはこの値を考慮することが重要です。
応用と計算例
平行平板コンデンサの蓄積エネルギー
コンデンサに蓄えられる静電エネルギー\(W\)は次のように計算できます:
\[ \begin{aligned} W &= \frac{1}{2}CV^2 \\[10pt] &= \frac{1}{2}QV \\[10pt] &= \frac{1}{2}\frac{Q^2}{C} \\[10pt] \end{aligned} \]
平行平板コンデンサの場合、体積当たりのエネルギー密度\(w\)は次のようになります:
\[ \begin{aligned} w &= \frac{W}{Sd} \\[10pt] &= \frac{1}{2}\varepsilon E^2 \\[10pt] &= \frac{1}{2}\frac{D^2}{\varepsilon} \\[10pt] &= \frac{1}{2}DE \\[10pt] \end{aligned} \]
例題:静電エネルギーの計算
面積\(S = 100 \; \mathrm{cm^2}\)、間隔\(d = 1 \; \mathrm{mm}\)、誘電体の比誘電率\(\varepsilon_r = 3\)の平行平板コンデンサに電圧\(V = 500 \; \mathrm{V}\)を印加した場合の静電エネルギーを求めよ。
解答:
まず静電容量を計算します:
\[ \begin{aligned} C &= \varepsilon_r \varepsilon_0 \frac{S}{d} \\[10pt] &= 3 \times 8.85 \times 10^{-12} \times \frac{100 \times 10^{-4}}{1 \times 10^{-3}} \\[10pt] &= 3 \times 8.85 \times 10^{-12} \times \frac{10^{-2}}{10^{-3}} \\[10pt] &= 3 \times 8.85 \times 10^{-11} \\[10pt] &= 265.5 \times 10^{-12} \; [\mathrm{F}] \\[10pt] &= 265.5 \; [\mathrm{pF}] \\[10pt] \end{aligned} \]
次に静電エネルギーを計算します:
\[ \begin{aligned} W &= \frac{1}{2}CV^2 \\[10pt] &= \frac{1}{2} \times 265.5 \times 10^{-12} \times 500^2 \\[10pt] &= \frac{1}{2} \times 265.5 \times 10^{-12} \times 250,000 \\[10pt] &= \frac{265.5 \times 250,000}{2} \times 10^{-12} \\[10pt] &= 33.2 \times 10^{-6} \; [\mathrm{J}] \\[10pt] &= 33.2 \; [\mu\mathrm{J}] \\[10pt] \end{aligned} \]
部分的に誘電体が挿入された場合
平行平板コンデンサに誘電体が部分的に挿入された場合、全体の静電容量は並列接続と見なせます:
\[ \begin{aligned} C_{\text{total}} = C_{\text{air}} + C_{\text{dielectric}} \\[10pt] \end{aligned} \]
誘電体の占める割合が面積比\(\alpha\)の場合:
\[ \begin{aligned} C_{\text{total}} &= \varepsilon_0 \frac{(1-\alpha)S}{d} + \varepsilon_r \varepsilon_0 \frac{\alpha S}{d} \\[10pt] &= \varepsilon_0 \frac{S}{d}(1-\alpha + \varepsilon_r \alpha) \\[10pt] &= C_0(1-\alpha + \varepsilon_r \alpha) \\[10pt] \end{aligned} \]
例題:部分挿入時の静電容量計算
面積\(S = 150 \; \mathrm{cm^2}\)、間隔\(d = 2 \; \mathrm{mm}\)の平行平板コンデンサがある。この中に比誘電率\(\varepsilon_r = 6\)の誘電体を面積の40%だけ挿入した場合の静電容量を求めよ。
解答:
与えられた値:
\(S = 150 \times 10^{-4} \; [\mathrm{m^2}]\)
\(d = 2 \times 10^{-3} \; [\mathrm{m}]\)
\(\varepsilon_r = 6\)
\(\alpha = 0.4\)(挿入率40%)
最初に空気中での静電容量\(C_0\)を計算します:
\[ \begin{aligned} C_0 &= \varepsilon_0 \frac{S}{d} \\[10pt] &= 8.85 \times 10^{-12} \times \frac{150 \times 10^{-4}}{2 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-12} \times \frac{1.5 \times 10^{-2}}{2 \times 10^{-3}} \\[10pt] &= 8.85 \times 10^{-12} \times 7.5 \\[10pt] &= 66.4 \times 10^{-12} \; [\mathrm{F}] \\[10pt] &= 66.4 \; [\mathrm{pF}] \\[10pt] \end{aligned} \]
次に部分挿入時の全体の静電容量\(C_{\text{total}}\)を計算します:
\[ \begin{aligned} C_{\text{total}} &= C_0(1-\alpha + \varepsilon_r \alpha) \\[10pt] &= 66.4 \times (1-0.4 + 6 \times 0.4) \\[10pt] &= 66.4 \times (0.6 + 2.4) \\[10pt] &= 66.4 \times 3 \\[10pt] &= 199.2 \; [\mathrm{pF}] \\[10pt] \end{aligned} \]
電界緩和のための電極設計
実際の高電圧機器では、電極の端部で電界が集中し、絶縁破壊が起きやすくなります。これを避けるために、電極の形状を工夫して電界を緩和する手法が用いられます。
電界緩和の主な方法
- 電極の端部を丸める
- シールド電極の使用
- ストレスコーンの使用
- 半導電層の使用
- 多段電極構造の採用
例えば、ブッシングのように円筒形の電極の場合、端部の電界\(E_{\text{edge}}\)は中央部の電界\(E_{\text{center}}\)より大きくなります:
\[ \begin{aligned} E_{\text{edge}} \approx \frac{2V}{r\ln(R/r)} \\[10pt] \end{aligned} \]
ここで、\(r\)は内部電極の半径、\(R\)は外部電極の半径、\(V\)は印加電圧です。
実用上の注意点
高電圧設備の設計では、電界集中を避けるための緩和対策が極めて重要です。特に、空気中の絶縁破壊電界強度は約3MV/mであるため、安全率を考慮して最大電界強度を1MV/m程度以下に抑えることが望ましいです。
異種誘電体境界での電界と電束密度
比誘電率の異なる二つの誘電体(\(\varepsilon_1\)と\(\varepsilon_2\))の境界面では、次の境界条件が成り立ちます:
境界条件
- 境界面に平行な電界成分は連続:\(E_{1\parallel} = E_{2\parallel}\)
- 境界面に垂直な電束密度成分は連続:\(D_{1\perp} = D_{2\perp}\)
この結果、境界面に垂直な電界成分は次の関係を持ちます:
\[ \begin{aligned} \frac{E_{1\perp}}{E_{2\perp}} = \frac{\varepsilon_2}{\varepsilon_1} \\[10pt] \end{aligned} \]
つまり、誘電率の小さい媒質中の方が電界が強くなります。このため、空気中(\(\varepsilon_r \approx 1\))と固体誘電体の境界では、空気中の電界が強くなり、絶縁破壊が起きやすくなります。
例題:異種誘電体境界での電界計算
比誘電率\(\varepsilon_{r1} = 1\)(空気)と\(\varepsilon_{r2} = 4\)(絶縁油)の境界面がある。境界面に垂直方向の電束密度が\(D_{\perp} = 5 \times 10^{-6} \; \mathrm{C/m^2}\)の場合、各媒質中の電界の垂直成分を求めよ。
解答:
電束密度の垂直成分は境界で連続なので:
\(D_{1\perp} = D_{2\perp} = 5 \times 10^{-6} \; [\mathrm{C/m^2}]\)
空気中の電界:
\[ \begin{aligned} E_{1\perp} &= \frac{D_{1\perp}}{\varepsilon_1} \\[10pt] &= \frac{5 \times 10^{-6}}{1 \times 8.85 \times 10^{-12}} \\[10pt] &= \frac{5 \times 10^{-6}}{8.85 \times 10^{-12}} \\[10pt] &= 5.65 \times 10^5 \; [\mathrm{V/m}] \\[10pt] \end{aligned} \]
絶縁油中の電界:
\[ \begin{aligned} E_{2\perp} &= \frac{D_{2\perp}}{\varepsilon_2} \\[10pt] &= \frac{5 \times 10^{-6}}{4 \times 8.85 \times 10^{-12}} \\[10pt] &= \frac{5 \times 10^{-6}}{35.4 \times 10^{-12}} \\[10pt] &= 1.41 \times 10^5 \; [\mathrm{V/m}] \\[10pt] \end{aligned} \]
このように、空気中の電界は絶縁油中の電界の4倍(\(\frac{\varepsilon_2}{\varepsilon_1} = 4\))になっています。
🔍 ワンポイントアドバイス: 電気力線と電界の問題を解く際は、まず対称性を見抜くことが重要です。平行平板では電界は一様で、点電荷では放射状というように、問題の構造に応じた電界の分布を想定すると解きやすくなります。また、誘電体境界の問題では、電束密度\(D\)の連続性を利用することがポイントです。第3種電気主任技術者試験では、誘電体を挿入した場合の静電容量変化や、部分挿入時の計算、異種誘電体境界での電界分布などが頻出します。特に、絶縁材料の選定と電界集中の影響を理解することは、実務上も重要な知識となります。
図のように,同じ寸法の直方体で誘電率の異なる二つの誘電体(比誘電率\( \ \varepsilon _{\mathrm {r1}} \ \)の誘電体\( \ 1 \ \)と比誘電率\( \ \varepsilon _{\mathrm {r2}} \ \)の誘電体\( \ 2 \ \))が平行板コンデンサに充填されている。極板間は一定の電圧\( \ V \ \mathrm {[V]} \ \)に保たれ,極板\( \ \mathrm {A} \ \)と極板\( \ \mathrm {B} \ \)にはそれぞれ\( \ +Q \ \mathrm {[C]} \ \)と\( \ -Q \ \mathrm {[C]} \ \)(\( \ Q \gt 0 \ \)) の電荷が蓄えられている。誘電体\( \ 1 \ \)と誘電体\( \ 2 \ \)は平面で接しており,その境界面は極板に対して垂直である。ただし,端効果は無視できるものとする。
この平行板コンデンサにおいて,極板\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)に平行な誘電体\( \ 1 \ \),誘電体\( \ 2 \ \)の断面をそれぞれ面\( \ \mathrm {S_{1}} \ \),面\( \ \mathrm {S_{2}} \ \)(面\( \ \mathrm {S_{1}} \ \)と面\( \ \mathrm {S_{2}} \ \)の断面積は等しい)とすると,面\( \ \mathrm {S_{1}} \ \)を貫く電気力線の総数(任意の点の電気力線の密度は,その点での電界の大きさを表す)は,面\( \ \mathrm {S_{2}} \ \)を貫く電気力線の総数の\( \ \fbox { (ア) } \ \)倍である。面\( \ \mathrm {S_{1}} \ \)を貫く電束の総数は面\( \ \mathrm {S_{2}} \ \)を貫く電束の総数の\( \ \fbox { (イ) } \ \)倍であり,面\( \ \mathrm {S_{1}} \ \)と面\( \ \mathrm {S_{2}} \ \)を貫く電束の数の総和は\( \ \fbox { (ウ) } \ \)である。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。

| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | 1 | \(\displaystyle \frac{\varepsilon_{\mathrm{r1}}}{\varepsilon_{\mathrm{r2}}}\) | \(Q\) |
| (2) | 1 | \(\displaystyle \frac{\varepsilon_{\mathrm{r1}}}{\varepsilon_{\mathrm{r2}}}\) | \(\displaystyle \frac{Q}{\varepsilon_{\mathrm{r1}}} + \frac{Q}{\varepsilon_{\mathrm{r2}}}\) |
| (3) | 1 | \(\displaystyle \frac{\varepsilon_{\mathrm{r2}}}{\varepsilon_{\mathrm{r1}}}\) | \(\displaystyle \frac{Q}{\varepsilon_{\mathrm{r1}}} + \frac{Q}{\varepsilon_{\mathrm{r2}}}\) |
| (4) | \(\displaystyle \frac{\varepsilon_{\mathrm{r2}}}{\varepsilon_{\mathrm{r1}}}\) | 1 | \(\displaystyle \frac{Q}{\varepsilon_{\mathrm{r1}}} + \frac{Q}{\varepsilon_{\mathrm{r2}}}\) |
| (5) | \(\displaystyle \frac{\varepsilon_{\mathrm{r2}}}{\varepsilon_{\mathrm{r1}}}\) | 1 | \(Q\) |
→ 横スクロールできます。
今日はな、電気力線と電束に関する問題を一緒に解いていこか。
平行板コンデンサに二つの誘電体が入っている状況やから、少し複雑に見えるかもしれへんけど、基本に戻って考えると理解しやすいで。
まずは問題文をよく読んで、何を聞かれてるか確認してみよか。
解説まとめ
■ 平行平板コンデンサの電界と電束とは
平行平板コンデンサは電気回路の基本素子であり、2枚の平行な導体板(電極)の間に誘電体を挟んだ構造です。この構造において、電界(電場)と電束密度は重要な物理量です。電界は単位電荷に働く力を表し、電束密度は単位面積あたりの電気力線の数(電束)を表します。異なる誘電体を持つ領域では、電界と電束密度の関係が変化するため、その特性を理解することが重要です。
■ 計算手順と公式
- 電界の計算
平行平板コンデンサ内の電界は、電圧と極板間距離から計算できます。
\( E = \frac{V}{d} \)
ここで、\(E\)は電界の大きさ[V/m]、\(V\)は電極間の電圧[V]、\(d\)は電極間の距離[m]です。
- 電束密度の計算
電束密度は、電界と誘電率の積で表されます。
\( D = \varepsilon E = \varepsilon_r \varepsilon_0 E \)
ここで、\(D\)は電束密度[C/m²]、\(\varepsilon\)は誘電率[F/m]、\(\varepsilon_r\)は比誘電率、\(\varepsilon_0\)は真空の誘電率(\(8.85 \times 10^{-12}\) [F/m])です。
- 電束の計算
電束は、電束密度と面積の積で表されます。
\( Q = D \times S \)
ここで、\(Q\)は電束[C]、\(S\)は面積[m²]です。
■ 具体的な計算例
問題条件
- 平行平板コンデンサの2つの領域に異なる誘電体が存在
- 誘電体1の比誘電率: \(\varepsilon_{r1}\)
- 誘電体2の比誘電率: \(\varepsilon_{r2}\)
- 極板間の電圧: \(V\)
- 極板間の距離: \(d\)
- 面積: \(S\)
(ア) 電界強度の比較
\[ \begin{aligned} \text{誘電体1内の電界:} \\ E_1 &= \frac{V}{d} \\[5pt] \text{誘電体2内の電界:} \\ E_2 &= \frac{V}{d} \\[5pt] \text{両者の比:} \\ \frac{E_1}{E_2} &= \frac{\frac{V}{d}}{\frac{V}{d}} = 1 \end{aligned} \]結論:両誘電体内の電界強度は等しい(比は1)。これは電気力線の密度と電界の大きさが比例することから、面S₁を貫く電気力線の総数は面S₂を貫く電気力線の総数の1倍となります。(解答:選択肢(1)(ア))
(イ) 電束の比較
\[ \begin{aligned} \text{誘電体1内の電束密度:} \\ D_1 &= \varepsilon_{r1}\varepsilon_0 E_1 \\[5pt] &= \varepsilon_{r1}\varepsilon_0 \frac{V}{d} \\[10pt] \text{誘電体2内の電束密度:} \\ D_2 &= \varepsilon_{r2}\varepsilon_0 E_2 \\[5pt] &= \varepsilon_{r2}\varepsilon_0 \frac{V}{d} \\[10pt] \text{誘電体1の電束:} \\ Q_1 &= D_1 S \\[5pt] &= \varepsilon_{r1}\varepsilon_0 \frac{V}{d} S \\[10pt] \text{誘電体2の電束:} \\ Q_2 &= D_2 S \\[5pt] &= \varepsilon_{r2}\varepsilon_0 \frac{V}{d} S \\[10pt] \text{両者の比:} \\ \frac{Q_1}{Q_2} &= \frac{\varepsilon_{r1}\varepsilon_0 \frac{V}{d} S}{\varepsilon_{r2}\varepsilon_0 \frac{V}{d} S} \\[5pt] &= \frac{\varepsilon_{r1}}{\varepsilon_{r2}} \end{aligned} \]結論:面S₁と面S₂を貫く電束の比は、両誘電体の比誘電率の比 \(\frac{\varepsilon_{r1}}{\varepsilon_{r2}}\) に等しい。
(ウ) 電束の総和
\[ \begin{aligned} \text{面S₁と面S₂を貫く電束の総和:} \\ Q_1 + Q_2 &= Q \end{aligned} \]結論:面S₁と面S₂を貫く電束の総和は、コンデンサに蓄えられる電荷量Qに等しい。
■ 実務上の留意点
平行平板コンデンサの電界と電束の理解は、電気機器の設計や絶縁設計において重要です。
- 異なる誘電体が接する境界面では、電界は連続的に変化せず、電束密度が連続となります。
- 高電圧機器の設計では、電界強度が絶縁破壊強度を超えないよう注意が必要です。
- コンデンサの容量設計では、誘電体の比誘電率と厚さが重要なパラメータとなります。
- 実際の機器では不均一な電界分布が生じることがあり、電界集中による絶縁破壊のリスクが高まります。
- 複合誘電体を用いたコンデンサでは、各層の電界強度と電束密度を適切に評価することが重要です。