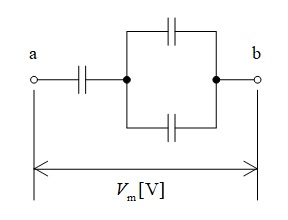
【理論】平成28年 問7|直列並列接続されたコンデンサ回路における最大印加電圧に関する計算問題
静電容量が \( 1 \ \mu\mathrm{F} \) のコンデンサ \( 3 \) 個を下図のように接続した回路を考える。
全てのコンデンサの電圧を \( 500 \ \mathrm{V} \) 以下にするために,\( a\text{-}b \) 間に加えることができる最大の電圧 \( V_{\mathrm{m}} \) の値 \( [\mathrm{V}] \) として,最も近いものを次の (1)~(5) のうちから一つ選べ。
ただし,各コンデンサの初期電荷は零とする。
合格への方程式
コンデンサの基本原理
コンデンサは電気回路において電荷を蓄える素子です。静電容量(キャパシタンス)は、コンデンサが蓄えることのできる電荷量を表す重要な指標です。
コンデンサの基本式
コンデンサに蓄えられる電荷 \(Q\) と端子間電圧 \(V\) の関係は次式で表されます:
\[ Q = C \times V \]
ここで:
\(Q\; [\mathrm{C}]\):電荷量(クーロン)
\(C\; [\mathrm{F}]\):静電容量(ファラド)
\(V\; [\mathrm{V}]\):端子間電圧(ボルト)
静電容量は、コンデンサの物理的構造によって決まります。平行平板コンデンサの場合、静電容量は次式で表されます:
\[ C = \varepsilon_0 \varepsilon_r \frac{S}{d} \]
ここで:
\(\varepsilon_0\; [\mathrm{F/m}]\):真空の誘電率(\(8.85 \times 10^{-12}\; \mathrm{F/m}\))
\(\varepsilon_r\):比誘電率(誘電体の種類による無次元量)
\(S\; [\mathrm{m^2}]\):電極の面積
\(d\; [\mathrm{m}]\):電極間の距離
静電容量の単位
静電容量の単位はファラド(F)ですが、実用的なコンデンサでは通常、マイクロファラド(μF = \(10^{-6}\)F)、ナノファラド(nF = \(10^{-9}\)F)、ピコファラド(pF = \(10^{-12}\)F)などの単位が使われます。
コンデンサにおけるエネルギー蓄積も重要な特性です。コンデンサに蓄えられるエネルギー \(W\) は次式で表されます:
\[ W = \frac{1}{2} C V^2 \]
ここで:
\(W\; [\mathrm{J}]\):エネルギー(ジュール)
\(C\; [\mathrm{F}]\):静電容量
\(V\; [\mathrm{V}]\):端子間電圧
コンデンサの直列・並列接続
複数のコンデンサを組み合わせた場合の合成静電容量は、接続方法によって異なります。ここでは、代表的な2つの接続方法について説明します。
並列接続の合成静電容量
コンデンサを並列に接続した場合、合成静電容量は各コンデンサの静電容量の和になります。
\[ C = C_1 + C_2 + C_3 + \cdots + C_n \]
二つのコンデンサの場合:
\[ C = C_1 + C_2 \]
並列接続では、各コンデンサの端子間電圧は同じですが、コンデンサ全体に流れる電流は各コンデンサの電流の和になります。電荷も同様に加算されるため、合成静電容量は各静電容量の和となります。
直列接続の合成静電容量
コンデンサを直列に接続した場合、合成静電容量の逆数は各コンデンサの静電容量の逆数の和になります。
\[ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \cdots + \frac{1}{C_n} \]
二つのコンデンサの場合:
\[ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} \]
これを変形すると:
\[ C = \frac{C_1 C_2}{C_1 + C_2} \]
直列接続では、各コンデンサに蓄えられる電荷量は同じですが、全体の電圧は各コンデンサの電圧の和になります。そのため、合成静電容量は常に個々のコンデンサの静電容量よりも小さくなります。
注意点
直列接続の場合、特に静電容量の異なるコンデンサを接続すると、各コンデンサにかかる電圧が異なります。小さな静電容量のコンデンサほど高い電圧がかかるため、耐電圧を超えないよう注意が必要です。
並列接続のイメージ:
\[ \begin{aligned} C_{並列} &= C_1 + C_2 \\[10pt] \end{aligned} \]
直列接続のイメージ:
\[ \begin{aligned} C_{直列} &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] \end{aligned} \]
並列と直列の物理的意味
並列接続は電極面積を増やすことに相当し、直列接続は電極間距離を増やすことに相当します。これが並列接続で容量が増加し、直列接続で容量が減少する理由です。
計算例題
例題1:並列接続の合成静電容量
静電容量が \(C_1 = 10\; \mathrm{\mu F}\) と \(C_2 = 15\; \mathrm{\mu F}\) の2つのコンデンサを並列接続した場合の合成静電容量を求めよ。
\[ \begin{aligned} C &= C_1 + C_2 \\[10pt] &= 10\; \mathrm{\mu F} + 15\; \mathrm{\mu F} \\[10pt] &= 25\; \mathrm{\mu F} \end{aligned} \]
例題2:直列接続の合成静電容量
静電容量が \(C_1 = 6\; \mathrm{\mu F}\) と \(C_2 = 12\; \mathrm{\mu F}\) の2つのコンデンサを直列接続した場合の合成静電容量を求めよ。
\[ \begin{aligned} C &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &= \frac{6\; \mathrm{\mu F} \times 12\; \mathrm{\mu F}}{6\; \mathrm{\mu F} + 12\; \mathrm{\mu F}} \\[10pt] &= \frac{72\; \mathrm{\mu F}^2}{18\; \mathrm{\mu F}} \\[10pt] &= 4\; \mathrm{\mu F} \end{aligned} \]
例題3:直列と並列の組み合わせ
下図のような回路の合成静電容量を求めよ。各コンデンサの静電容量は \(C_1 = C_3 = 3\; \mathrm{\mu F}\)、\(C_2 = 6\; \mathrm{\mu F}\) とする。
(回路図:\(C_1\) と \(C_2\) が直列接続され、その組み合わせと \(C_3\) が並列接続されている)
\[ \begin{aligned} \text{まず}、C_1 と C_2 の直列合成:C_{12} &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &= \frac{3\; \mathrm{\mu F} \times 6\; \mathrm{\mu F}}{3\; \mathrm{\mu F} + 6\; \mathrm{\mu F}} \\[10pt] &= \frac{18\; \mathrm{\mu F}^2}{9\; \mathrm{\mu F}} \\[10pt] &= 2\; \mathrm{\mu F} \\[10pt] \text{次に}、C_{12} と C_3 の並列合成:C &= C_{12} + C_3 \\[10pt] &= 2\; \mathrm{\mu F} + 3\; \mathrm{\mu F} \\[10pt] &= 5\; \mathrm{\mu F} \end{aligned} \]
→ 横スクロールして下さい
計算のポイント
複雑な回路の合成静電容量を求める際は、次のステップで計算します:
1. 直列または並列の単純な部分回路に分解する
2. 各部分回路の合成静電容量を計算する
3. 部分回路を合成して全体の静電容量を求める
応用と発展
コンデンサの応用例
コンデンサの直列・並列接続の特性は、様々な電気回路で活用されています:
1. 電源のスムージング:並列接続による大容量化で電源のリップルを低減
2. フィルタ回路:特定の周波数を通過・遮断するRC回路
3. タイミング回路:時定数を利用した時間遅延回路
4. 共振回路:LC回路による特定周波数の共振
5. 電圧分圧回路:直列接続による高電圧の分圧
コンデンサの周波数特性
コンデンサのリアクタンス \(X_C\) は周波数に反比例します:
\[ X_C = \frac{1}{2\pi f C} \]
ここで:
\(X_C\; [\Omega]\):容量性リアクタンス
\(f\; [\mathrm{Hz}]\):周波数
\(C\; [\mathrm{F}]\):静電容量
この特性から、コンデンサは周波数が高くなるほど低いインピーダンスを示します。そのため、直流電流は通さず、交流電流は通す特性があります。
コンデンサバンクの設計
大容量のコンデンサバンク(例:電力用力率改善装置)では、耐電圧と容量を考慮した直列・並列の組み合わせが重要です:
1. 必要な耐電圧を確保するための直列接続
2. 必要な静電容量を確保するための並列接続
3. 各コンデンサの電圧バランスを取るための抵抗(均圧抵抗)の設置
発展例題:電圧分担
静電容量が \(C_1 = 4\; \mathrm{\mu F}\) と \(C_2 = 8\; \mathrm{\mu F}\) の2つのコンデンサを直列接続し、全体に \(120\; \mathrm{V}\) の電圧をかけた場合、各コンデンサにかかる電圧を求めよ。
\[ \begin{aligned} \text{全体の静電容量:} C &= \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &= \frac{4\; \mathrm{\mu F} \times 8\; \mathrm{\mu F}}{4\; \mathrm{\mu F} + 8\; \mathrm{\mu F}} \\[10pt] &= \frac{32\; \mathrm{\mu F}^2}{12\; \mathrm{\mu F}} \\[10pt] &= \frac{8}{3}\; \mathrm{\mu F} \\[10pt] \text{全体の電荷量:} Q &= C \times V \\[10pt] &= \frac{8}{3}\; \mathrm{\mu F} \times 120\; \mathrm{V} \\[10pt] &= 320\; \mathrm{\mu C} \\[10pt] \text{直列接続では、電荷量は同じなので:} \\[10pt] V_1 &= \frac{Q}{C_1} = \frac{320\; \mathrm{\mu C}}{4\; \mathrm{\mu F}} = 80\; \mathrm{V} \\[10pt] V_2 &= \frac{Q}{C_2} = \frac{320\; \mathrm{\mu C}}{8\; \mathrm{\mu F}} = 40\; \mathrm{V} \\[10pt] \end{aligned} \]
→ 横スクロールして下さい
確認:\(V_1 + V_2 = 80\; \mathrm{V} + 40\; \mathrm{V} = 120\; \mathrm{V}\)
このように、直列接続では静電容量に反比例して電圧が分担されます。容量の小さいコンデンサほど高い電圧がかかります。
現実のコンデンサにおける注意点
実際のコンデンサでは、以下の点に注意する必要があります:
1. 漏れ電流:理想的なコンデンサは絶縁体で完全に絶縁されているが、実際には微小な漏れ電流が存在
2. 等価直列抵抗(ESR):コンデンサの電極や端子の抵抗による損失
3. 等価直列インダクタンス(ESL):高周波領域での寄生インダクタンス
4. 温度特性:温度変化による容量値の変動
5. 経年変化:時間経過による容量低下や特性変化
🔍 ワンポイントアドバイス: コンデンサの直列・並列接続をよく理解するために、水タンクのアナロジーを考えてみましょう。並列接続は複数のタンクを横に並べるようなもので、水(電荷)の総貯水量(静電容量)は増えます。一方、直列接続は縦に細長いタンクを作るようなもので、同じ水量(電荷)でも水位(電圧)が高くなります。また、第3種電気主任技術者試験では、複雑な回路の合成静電容量を求める問題がよく出題されるので、段階的に部分回路に分解して計算する方法をマスターしておきましょう。
今日はコンデンサの直列・並列接続の問題を解いていくで!まずは問題文を読んでみよか。
この問題では、コンデンサの直列・並列接続があって、最大電圧を求めるんや。まず並列部分から考えていこか。静電容量1μFのコンデンサが2つ並列になっとるけど、並列接続のコンデンサの合成容量はどないなるか知っとる?
はい、先生!並列接続の場合は、静電容量を足し算します。なので、\(1\,\mu\mathrm{F} + 1\,\mu\mathrm{F} = 2\,\mu\mathrm{F}\)になります。
並列接続の合成静電容量の公式は次のようになります:
\( C_{\mathrm{合成}} = C_1 + C_2 + C_3 + ... + C_n \)
そうや!正解や!並列接続の場合は静電容量を足し算するんや。だから、下の図みたいに\(1\,\mu\mathrm{F}\)と\(1\,\mu\mathrm{F}\)の並列接続なら\(2\,\mu\mathrm{F}\)になる。
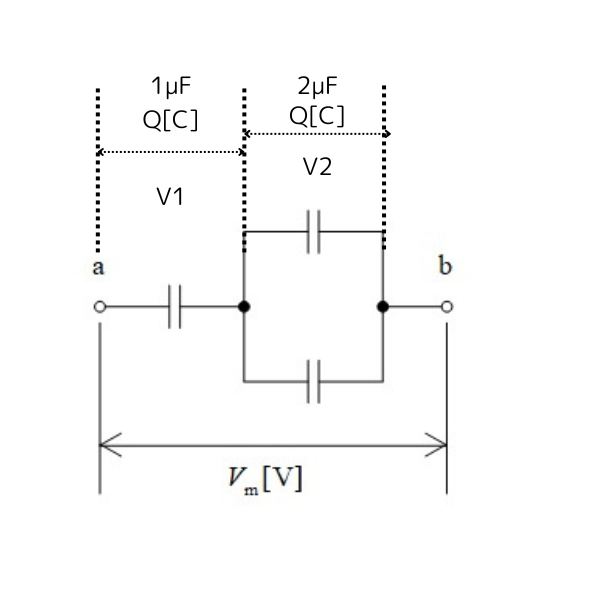
次は、この回路全体の最大電圧を考えるんやけど、まず直列接続したコンデンサの特徴について考えよか。直列接続したコンデンサには何が等しくなるか覚えてる?
はい!直列接続したコンデンサには「電荷\(Q\)」が等しくなります。どのコンデンサにも同じ量の電荷が蓄えられます。
これに対して、電圧は各コンデンサの静電容量によって分配されます。
ええ答えやな!直列接続したコンデンサには電荷\(Q\)が等しくなるんや。そこで、各コンデンサにかかる電圧を考えてみよか。
コンデンサの電荷\(Q\)と静電容量\(C\)と電圧\(V\)の関係式を思い出してみ?
コンデンサの電荷\(Q\)、静電容量\(C\)、電圧\(V\)の関係式は:
\( Q = CV \) または \( V = \frac{Q}{C} \) です。
電荷は静電容量と電圧の積、あるいは電圧は電荷を静電容量で割ったものになります。
そのとおり!じゃあ、この関係式を使って、直列になっとる\(1\,\mu\mathrm{F}\)のコンデンサと\(2\,\mu\mathrm{F}\)のコンデンサにかかる電圧\(V_1\)と\(V_2\)を求めてみよか。電荷は\(Q\)で同じやから、それぞれの静電容量に応じた電圧になるはずや。
はい、それぞれの電圧を求めてみます。
V₁(1μFのコンデンサの電圧):
\[ \begin{aligned} V_1 &= \frac{Q}{C_1} \\ &= \frac{Q}{1 \times 10^{-6}} \\ &= Q \times 10^6 \mathrm{[V]} \end{aligned} \]V₂(2μFのコンデンサの電圧):
\[ \begin{aligned} V_2 &= \frac{Q}{C_2} \\ &= \frac{Q}{2 \times 10^{-6}} \\ &= \frac{Q}{2} \times 10^6 \mathrm{[V]} \end{aligned} \]ナイス計算や!ちょっと比較してみようか。\(V_1\)と\(V_2\)の関係はどうなるかな?
V₁とV₂の関係を比較してみます。
\(V_1 = Q \times 10^6\) [V]
\(V_2 = \frac{Q}{2} \times 10^6\) [V] \(= \frac{Q \times 10^6}{2}\) [V]
これを比較すると:
\[ \begin{aligned} V_1 &= Q \times 10^6 \\ &= 2 \times \frac{Q \times 10^6}{2} \\ &= 2 \times V_2 \end{aligned} \]つまり、\(V_1 = 2V_2\) という関係があります。静電容量が\(1:2\)なので、電圧は\(2:1\)の比率になりました。静電容量が小さいほど、同じ電荷に対して大きな電圧がかかることがわかります。
よう考えられとるな!静電容量が小さいほど電圧は大きくなるんや。だから、静電容量が\(1\,\mu\mathrm{F}\)のコンデンサの方が、\(2\,\mu\mathrm{F}\)のコンデンサよりも2倍の電圧がかかる。
さて、問題ではコンデンサの耐電圧が\(500\,\mathrm{V}\)と決まっとるんやった。この条件から最大電圧はどう求めたらええかな?
最大電圧を求めるには、どのコンデンサも耐電圧の\(500\,\mathrm{V}\)を超えないようにする必要があります。
先ほど求めたように、\(V_1 = 2V_2\) という関係があるので、\(V_1\)の方が大きい電圧がかかります。したがって、\(V_1\)が\(500\,\mathrm{V}\)以下になるように設定すれば、\(V_2\)は自動的に\(250\,\mathrm{V}\)以下になります。
したがって:
\(V_1 = 500\,\mathrm{V}\)(限界値)
\(V_2 = 250\,\mathrm{V}\)(\(V_1\)の半分)
回路全体の電圧\(V_m\)は、直列接続のコンデンサの電圧の和になるので:
\[ \begin{aligned} V_m &= V_1 + V_2 \\ &= 500 + 250 \\ &= 750 \mathrm{[V]} \end{aligned} \]したがって、加えることができる最大電圧は750Vとなります。
選択肢の(3)が答えになります
素晴らしい解き方や!重要なポイントをまとめよか。
1. まず並列接続の部分を合成して、\(1\,\mu \mathrm{F} + 1\,\mu \mathrm{F} = 2\,\mu \mathrm{F}\)にした
2. 直列接続では電荷\(Q\)が等しくなるから、\(V = \frac{Q}{C}\)の関係で電圧を求めた
3. 静電容量が\(1:2\)だから、電圧は\(2:1\)の比率になった
4. 耐電圧\(500\,\mathrm{V}\)を考慮すると、\(V_1 = 500\,\mathrm{V}\)、\(V_2 = 250\,\mathrm{V}\)が限界値
5. 直列接続の合成電圧は\(V_1+V_2\)だから、最大電圧は\(750\,\mathrm{V}\)になる
このように、コンデンサの直列・並列接続では、静電容量と電圧の関係をしっかり理解することが大事やな!
はい、先生!とても分かりやすかったです。
特に重要なのは:
・並列接続では静電容量を足し算する(\(C = C_1 + C_2\))
・直列接続では電荷\(Q\)が等しくなる
・静電容量\(C\)が小さいほど、同じ電荷\(Q\)に対して大きな電圧\(V\)がかかる(\(V = \frac{Q}{C}\))
・直列接続の合成電圧は各コンデンサの電圧の和になる(\(V = V_1 + V_2\))
これらの原理を理解すれば、コンデンサの問題を解くことができますね!
解説まとめ
■ コンデンサの直列・並列接続とは
コンデンサ回路において、直列接続と並列接続は基本的な結合方法です。それぞれの接続方法によって、合成静電容量の計算方法や電圧・電荷の分配が異なります。並列接続では各コンデンサの電圧は同じで電荷は異なり、直列接続では各コンデンサの電荷は同じで電圧は異なります。電気回路の設計において、コンデンサの接続方法の特性を理解することは重要です。
■ 計算手順と公式
- コンデンサの合成静電容量の計算
コンデンサの接続方法によって、合成静電容量の計算式が異なります。
並列接続: \( C = C_1 + C_2 \)
直列接続: \( \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} \) または \( C = \frac{C_1 C_2}{C_1 + C_2} \)
- コンデンサの電圧と電荷の関係
コンデンサに蓄えられる電荷Qと電圧Vの関係は静電容量Cを用いて表されます。
\( Q = CV \) または \( V = \frac{Q}{C} \)
- 直列接続でのコンデンサの電圧分配
直列接続したコンデンサでは、電荷が等しく、電圧は静電容量に反比例して分配されます。
\( \frac{V_1}{V_2} = \frac{C_2}{C_1} \)
- コンデンサ回路の最大許容電圧の計算
各コンデンサの耐電圧を考慮した回路全体の最大許容電圧を計算します。
■ 具体的な計算例
問題条件
- 図のようなコンデンサ回路
- 各コンデンサの静電容量: 上部左右に1μF、上部中央と下部に2μF
- 各コンデンサの最大許容電圧: 500 V
- 求めるのは、回路全体に加えることができる最大電圧 Vm
回路の等価変換

上部左側の2つの1μFコンデンサは並列接続なので、合成静電容量は:
\[ \begin{aligned} C_{\text{並列}} &= 1 \ \mu\text{F} + 1 \ \mu\text{F} \\[5pt] &= 2 \ \mu\text{F} \end{aligned} \]よって、図は左側に2μF、右側に2μFの直列接続に変換できます。
直列接続したコンデンサの電圧分配
左側のコンデンサに蓄えられる電荷:
\[ \begin{aligned} Q &= C_1 V_1 \\[5pt] V_1 &= \frac{Q}{C_1} = \frac{Q}{1 \times 10^{-6}} = Q \times 10^6 \ \mathrm{[V]} \end{aligned} \]右側のコンデンサに蓄えられる電荷:
\[ \begin{aligned} Q &= C_2 V_2 \\[5pt] V_2 &= \frac{Q}{C_2} = \frac{Q}{2 \times 10^{-6}} = \frac{Q}{2} \times 10^6 \ \mathrm{[V]} \end{aligned} \]電圧の比:
\[ \begin{aligned} \frac{V_1}{V_2} &= \frac{C_2}{C_1} = \frac{2 \ \mu\mathrm{F}}{1 \ \mu\mathrm{F}} = 2 \\[5pt] V_1 &= 2V_2 \end{aligned} \]最大許容電圧の計算
各コンデンサの最大許容電圧は500 Vなので:
\[ \begin{aligned} V_1 &\leq 500 \ \mathrm{V} \end{aligned} \]これより:
\[ \begin{aligned} V_2 &= \frac{V_1}{2} \leq \frac{500}{2} = 250 \ \mathrm{V} \end{aligned} \]回路全体の最大電圧:
\[ \begin{aligned} V_m &= V_1 + V_2 \\[5pt] &= 500 + 250 \\[5pt] &= 750 \ \mathrm{V} \end{aligned} \]結論:回路全体に加えることができる最大電圧は 750 [V] である。(解答:選択肢(3))
■ 実務上の留意点
コンデンサ回路の設計と電圧分配の理解は、電気機器設計において重要です。
- 高電圧回路では、単一コンデンサの耐電圧を超える場合、複数コンデンサの直列接続を用いることがあります。
- 直列接続したコンデンサには電圧均等化のための抵抗(ブリーダ抵抗)を並列接続することが望ましいです。これにより、漏れ電流の差によるコンデンサ間の電圧アンバランスを防ぎます。
- 実際の回路では、コンデンサの製造公差も考慮する必要があり、定格よりも余裕を持った設計が求められます。
- 電源投入時の突入電流や充電時定数の違いによる過渡的な電圧分配の不均一にも注意が必要です。
- 温度変化や経年劣化によるコンデンサ特性の変化も、特に安全性が重要な回路では考慮すべき要素です。