【理論】平成24年 問1|コンデンサ回路におけるスイッチ動作後の電圧比に関する計算問題
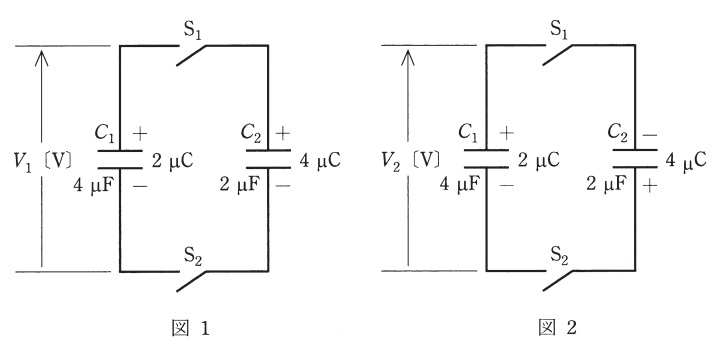
図\( 1 \) 及び図\( 2 \) のように、静電容量がそれぞれ \( 4 \) [μF] と \( 2 \) [μF] のコンデンサ \( C_1 \) 及び \( C_2 \),スイッチ \( S_1 \) 及び \( S_2 \) からなる回路がある。
コンデンサ \( C_1 \) と \( C_2 \) には、それぞれ \( 2 \) [μC] と \( 4 \) [μC] の電荷が図のような極性で蓄えられている。
この状態から両図ともスイッチ \( S_1 \) 及び \( S_2 \) を閉じたとき、図\( 1 \) のコンデンサ \( C_1 \) の端子電圧を \( V_1 \) [V],図\( 2 \) のコンデンサ \( C_1 \) の端子電圧を \( V_2 \) [V] とすると,電圧比 \( \left| \frac{V_1}{V_2} \right| \) の値として,正しいものを次の \( (1) \) ~ \( (5) \) のうちから一つ選べ。
なお,\( xyz \) 座標の定義は,破線の枠内の図で示したとおりとする。
合格への方程式
平行平板コンデンサの基本公式
平行平板コンデンサは、平行に配置された2枚の導体板(極板)の間に誘電体を挟んだ構造を持つ基本的なコンデンサです。
基本パラメータ:
- 極板の面積: S [m²]
- 極板間の距離: d [m]
- 誘電体の比誘電率: εr
- 真空の誘電率: ε0 = 8.85×10-12 [F/m]
1. 静電容量の公式:
\[ \begin{eqnarray} C &=& \frac{\varepsilon_r \varepsilon_0 S}{d} \end{eqnarray} \]
2. 電荷と電圧の関係:
\[ \begin{eqnarray} Q &=& CV \end{eqnarray} \]
3. 電界の強さ:
\[ \begin{eqnarray} E &=& \frac{V}{d} \end{eqnarray} \]
これらの公式は相互に関連しています。例えば、蓄えられる電荷を極板の面積などで表すには、式(1)と式(2)を組み合わせて:
\[ \begin{eqnarray} Q &=& CV \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 S}{d} \times V \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 SV}{d} \end{eqnarray} \]
静電容量の理解
静電容量とは、コンデンサが電荷を蓄える能力を表す物理量です。
静電容量の物理的意味:
静電容量 C [F] は、コンデンサに1ボルトの電圧をかけたときに蓄えられる電荷の量 [C] を示します。
平行平板コンデンサの静電容量に影響を与える要素:
- 極板の面積 S:面積が大きいほど静電容量は大きくなる(比例関係)
- 極板間の距離 d:距離が大きいほど静電容量は小さくなる(反比例関係)
- 誘電体の種類(比誘電率 εr):比誘電率が大きいほど静電容量は大きくなる(比例関係)
比誘電率とは:
比誘電率は、真空と比較してどれだけ電荷を蓄えられるかを表す無次元の係数です。
| 物質 | 比誘電率(εr) |
|---|---|
| 真空 | 1.0 |
| 空気 | 1.0006 |
| 紙 | 2.0~3.0 |
| ガラス | 4.0~7.0 |
| セラミック | 10~10,000以上 |
静電容量の単位:
静電容量の単位はファラド [F] ですが、実際のコンデンサでは μF(10-6 F)、nF(10-9 F)、pF(10-12 F)などの単位が使われることが多いです。
コンデンサに蓄えられるエネルギー
コンデンサは電荷を蓄えることでエネルギーを保存できます。
蓄積エネルギーの公式:
\[ \begin{eqnarray} U &=& \frac{1}{2}CV^2 \end{eqnarray} \]
この公式を極板の面積や距離などで表すと:
\[ \begin{eqnarray} U &=& \frac{1}{2}CV^2 \\[10pt] &=& \frac{1}{2} \times \frac{\varepsilon_r \varepsilon_0 S}{d} \times V^2 \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 SV^2}{2d} \end{eqnarray} \]
電界の強さ E = V/d を用いると:
\[ \begin{eqnarray} U &=& \frac{\varepsilon_r \varepsilon_0 SV^2}{2d} \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 S}{2} \times \frac{V^2}{d} \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 S}{2} \times E \times V \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 SE^2d}{2} \end{eqnarray} \]
エネルギー密度:
コンデンサ内部の単位体積あたりのエネルギー(エネルギー密度)は:
\[ \begin{eqnarray} \text{エネルギー密度} &=& \frac{U}{Sd} \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 SE^2d}{2} \times \frac{1}{Sd} \\[10pt] &=& \frac{\varepsilon_r \varepsilon_0 E^2}{2} \text{ [J/m³]} \end{eqnarray} \]
このエネルギーは、コンデンサが放電するときに外部回路に供給されます。これがフラッシュライトやカメラのフラッシュなどで利用されるエネルギーの源です。
コンデンサの接続と合成静電容量
複数のコンデンサを組み合わせた場合の合成静電容量の計算方法を見てみましょう。
1. 並列接続:
静電容量 C1 と C2 のコンデンサを並列に接続した場合の合成静電容量 C は:
\[ \begin{eqnarray} C &=& C_1 + C_2 \end{eqnarray} \]
これは極板の面積が実質的に増えることを意味します。
2. 直列接続:
静電容量 C1 と C2 のコンデンサを直列に接続した場合の合成静電容量 C は:
\[ \begin{eqnarray} \frac{1}{C} &=& \frac{1}{C_1} + \frac{1}{C_2} \\[10pt] C &=& \frac{C_1 C_2}{C_1 + C_2} \end{eqnarray} \]
これは実質的に極板間の距離が増えることを意味します。
並列接続と直列接続の特徴:
- 並列接続:合成静電容量は個々の静電容量の和(C > C1, C > C2)
- 直列接続:合成静電容量は常に個々の静電容量より小さい(C < C1, C < C2)
コンデンサを接続する方法によって、蓄えられる電荷量や電圧の分配が変わります:
- 並列接続:各コンデンサにかかる電圧は同じ、蓄える電荷は静電容量に比例
- 直列接続:各コンデンサが蓄える電荷は同じ、各コンデンサにかかる電圧は静電容量に反比例
計算問題
平行平板コンデンサの基本公式を活用した計算問題を解いてみましょう。
問題1:
面積 S = 100 cm² (= 0.01 m²)、間隔 d = 0.5 mm (= 0.0005 m) の平行平板の間に比誘電率 εr = 4.0 の誘電体を挟んだコンデンサがあります。このコンデンサの静電容量を求めなさい。
解答:
\[ \begin{aligned} C &= \frac{\varepsilon_r \varepsilon_0 S}{d} \\[10pt] &= \frac{4.0 \times 8.85 \times 10^{-12} \,\text{F/m} \times 0.01 \,\text{m}^2} {0.0005 \,\text{m}} \\[10pt] &= \frac{4.0 \times 8.85 \times 10^{-12} \times 0.01}{0.0005} \,\text{F} \\[10pt] &= 4.0 \times 8.85 \times 10^{-12} \times \frac{0.01}{0.0005} \,\text{F} \\[10pt] &= 4.0 \times 8.85 \times 10^{-12} \times 20 \,\text{F} \\[10pt] &= 7.08 \times 10^{-10} \,\text{F} \\[10pt] &= 708 \,\text{pF} \end{aligned} \]
問題2:
上記のコンデンサに 100 V の電圧をかけると、どれだけの電荷が蓄えられますか?また、そのときに蓄えられるエネルギーを求めなさい。
解答(電荷):
\[ \begin{eqnarray} Q &=& CV \\[10pt] &=& 7.08 \times 10^{-10} \text{ F} \times 100 \text{ V} \\[10pt] &=& 7.08 \times 10^{-8} \text{ C} \\[10pt] &=& 70.8 \text{ nC} \end{eqnarray} \]
解答(エネルギー):
\[ \begin{eqnarray} U &=& \frac{1}{2}CV^2 \\[10pt] &=& \frac{1}{2} \times 7.08 \times 10^{-10} \text{ F} \times (100 \text{ V})^2 \\[10pt] &=& \frac{1}{2} \times 7.08 \times 10^{-10} \times 10000 \text{ J} \\[10pt] &=& 3.54 \times 10^{-6} \text{ J} \\[10pt] &=& 3.54 \text{ μJ} \end{eqnarray} \]
問題3:
静電容量 C1 = 200 pF、C2 = 300 pF のコンデンサを(1)並列接続と(2)直列接続した場合の合成静電容量を求めなさい。
解答(1)並列接続:
\[ \begin{eqnarray} C &=& C_1 + C_2 \\[10pt] &=& 200 \text{ pF} + 300 \text{ pF} \\[10pt] &=& 500 \text{ pF} \end{eqnarray} \]
解答(2)直列接続:
\[ \begin{eqnarray} C &=& \frac{C_1 C_2}{C_1 + C_2} \\[10pt] &=& \frac{200 \text{ pF} \times 300 \text{ pF}}{200 \text{ pF} + 300 \text{ pF}} \\[10pt] &=& \frac{60000 \text{ pF}^2}{500 \text{ pF}} \\[10pt] &=& 120 \text{ pF} \end{eqnarray} \]
🔍 ワンポイントアドバイス: 平行平板コンデンサの公式を使いこなすには、単に式を覚えるだけでなく、各パラメータ(面積S、距離d、比誘電率εrなど)が静電容量や蓄えられる電荷にどう影響するかを理解することが重要です。特に注目すべきは、電荷Q、静電容量C、電圧Vの関係式(Q=CV)と、静電容量の公式(C=εrε0S/d)の組み合わせです。これにより、「極板間距離を2倍にすると電荷はどうなるか」といった応用問題も解けるようになります。また、単位の変換(mm→m、cm²→m²など)にも注意しましょう。
今日はコンデンサの電荷と電圧の関係について勉強するで!スイッチの開閉によって、コンデンサにどんな変化が起こるか見ていこか。まずはこの問題を考えてみるで。
図1と図2があって、図1ではコンデンサC1(2μF)とC2(4μF)が並列に接続されていて、C1には2μCの電荷が、C2には4μCの電荷がたまっている状態や。そこでスイッチを閉じると図2のように接続が変わるんやけど、このときの電圧の比はどうなるか考えてみよか。
まず大事な法則を思い出してみ。スイッチを閉じる前後で全体の電荷量はどうなる?
はい、先生!スイッチを閉じる前後で全体の電荷量は変わりません。電荷保存の法則により、回路内の総電荷量は一定に保たれます。
その通りや!電荷は保存されるんや。じゃあ、図1でのC1とC2に蓄えられてる電荷量Q1はいくらやろ?
図1での全電荷量Q1は、C1とC2にたまっている電荷の合計になります。
\[ \begin{aligned} Q_1 &= 2 + 4 \\ &= 6 \ \mathrm{[\mu C]} \end{aligned} \]よって、図1での全電荷量は6μCです。
ええやん!計算合ってるで。図1では上側が+になってるから、電荷の向きも考えて6μCやな。
次に、図2ではどうなるんやろ?スイッチを閉じた後、C1とC2の接続が変わるけど、電荷量Q2はどうなる?
図2では、C1とC2の接続が変わり、極性も変わっています。図2では下側が+になっていますので、それを考慮して計算します。
図2でのC1の電荷は初期状態と逆向きになるので-2μC、C2の電荷は4μCのままです。よって全電荷量Q2は:
\[ \begin{aligned} Q_2 &= 4 - 2 \\ &= 2 \ \mathrm{[\mu C]} \end{aligned} \]つまり、図2での全電荷量は2μCとなります。
よく考えられてるな!図2では極性が変わって、C1は-2μC、C2は+4μCだから、合計で+2μCになるんやね。
さて、次はこの回路の合成静電容量Cを求めよう。C1とC2が並列接続されているときの合成静電容量はどう計算する?
並列接続されたコンデンサの合成静電容量は、個々の静電容量の和になります。
\[ \begin{aligned} C &= C_1 + C_2 \\ &= 2 + 4 \\ &= 6 \ \mathrm{[\mu F]} \end{aligned} \]したがって、合成静電容量Cは6μFとなります。
その通り!並列回路の合成静電容量は足し算やな。C = C1 + C2 = 6μF。
さあ、ここからが大事やで。スイッチを閉じた後のそれぞれのコンデンサにかかる電圧V1とV2を求めよう。電圧Vと電荷Qと静電容量Cの関係式覚えてるか?
はい、先生!コンデンサの電圧V、電荷Q、静電容量Cの関係式は:
\( V = \frac{Q}{C} \)
この式を使って、V1とV2を計算します。
\[ \begin{aligned} V_1 &= \frac{Q_1}{C} \\ &= \frac{6 \times 10^{-6}}{6 \times 10^{-6}} \\ &= 1 \ \mathrm{[V]} \\[10pt] V_2 &= \frac{Q_2}{C} \\ &= \frac{2 \times 10^{-6}}{6 \times 10^{-6}} \\ &= \frac{1}{3} \ \mathrm{[V]} \end{aligned} \]あ、図2では下側が+になっているので、上から見た場合は電圧が負になりますね。正確には:
\[ V_2 = -\frac{1}{3} \ \mathrm{[V]} \]ほんまによう分かってるな!V2の符号に気づいたのはエライ!図2では下側が+だから、上から見ると-1/3 Vになるんやね。
さて、最後の問題や。電圧比|V1/V2|を求めてみよう。絶対値の計算やから、符号には気をつけてな。
はい、電圧比の絶対値|V1/V2|を計算します。
\[ \begin{aligned} \left| \frac{V_1}{V_2} \right| &= \left| \frac{1}{-\frac{1}{3}} \right| \\ &= \left| -3 \right| \\ &= 3 \end{aligned} \]したがって、電圧比の絶対値は3になります。
完璧や!計算も理解もばっちりやね!
まとめると、コンデンサの問題を解く時のポイントは次のようなものやで:
- 電荷保存の法則を使う(スイッチ開閉前後で全体の電荷量は変わらない)
- コンデンサの極性(向き)に注意して電荷を計算する
- 並列接続の合成静電容量は C = C1 + C2
- 電圧は V = Q/C で計算できる
- 極性が変わると電圧の符号が変わることに注意
こういう問題は第三種電気主任技術者試験でもよく出るから、しっかり覚えておいてな!
他に質問ある?
はい、先生!1つ質問があります。もしコンデンサが直列接続されている場合、合成静電容量はどのように計算するのでしょうか?また、その場合の電圧と電荷の関係も変わりますか?
ええ質問やな!コンデンサが直列接続されてる場合は、合成静電容量の計算が違うんや。
直列接続の場合の合成静電容量Cは次の式で計算するんや:
\[ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} \]または
\[ C = \frac{C_1 \times C_2}{C_1 + C_2} \]これは抵抗の並列接続と同じ形やから覚えやすいやろ?
また、直列接続では電荷Qは各コンデンサで同じになるけど、電圧は分圧されるんや。電圧の分配は静電容量に反比例する。つまり、静電容量が小さいコンデンサほど、大きな電圧がかかるんや。
例えば、2μFと4μFの直列接続では、2μFの方が4μFの2倍の電圧がかかることになるんや。
練習問題をやってみるか?
はい、先生!練習問題をやってみたいです。直列接続の式が抵抗の並列接続と同じ形なのはとても覚えやすいですね。また、電圧が静電容量に反比例するという点も理解できました。
よし、じゃあ練習問題やってみよか!
C1 = 3μF、C2 = 6μFのコンデンサが直列接続されていて、全体に12Vの電圧がかかっているとする。このとき:
- 合成静電容量Cを求めよ
- 各コンデンサにかかる電圧V1とV2を求めよ
- 各コンデンサに蓄えられる電荷Qを求めよ
まずは合成静電容量からやってみ!
はい、先生!直列接続の合成静電容量の公式を使います。
\[ \begin{aligned} C &= \frac{C_1 \times C_2}{C_1 + C_2} \\ &= \frac{3 \times 6}{3 + 6} \\ &= \frac{18}{9} \\ &= 2 \ \mathrm{[\mu F]} \end{aligned} \]したがって、合成静電容量Cは2μFです。
ええやん!計算合ってるで。3μFと6μFの直列接続だと2μFになるんやね。
次に、各コンデンサにかかる電圧V1とV2を求めてみよか。電圧の分配則を使うんやで。
はい、先生!直列接続での電圧の分配は静電容量に反比例します。全体の電圧が12Vですので:
\[ \begin{aligned} V_1 &= 12 \times \frac{C_2}{C_1 + C_2} \\ &= 12 \times \frac{6}{3 + 6} \\ &= 12 \times \frac{6}{9} \\ &= 12 \times \frac{2}{3} \\ &= 8 \ \mathrm{[V]} \\[10pt] V_2 &= 12 \times \frac{C_1}{C_1 + C_2} \\ &= 12 \times \frac{3}{3 + 6} \\ &= 12 \times \frac{3}{9} \\ &= 12 \times \frac{1}{3} \\ &= 4 \ \mathrm{[V]} \end{aligned} \]したがって、C1には8V、C2には4Vの電圧がかかります。静電容量が小さいC1の方が大きな電圧がかかっていることが確認できます。
ようできてるな!電圧の分配則をちゃんと使えてるで。静電容量が小さいC1(3μF)の方が大きな電圧(8V)がかかるんやね。
最後に、各コンデンサに蓄えられる電荷Qを求めてみよか。公式を思い出してやってみ!
はい、先生!コンデンサの電荷は Q = C × V で計算できます。
\[ \begin{aligned} Q_1 &= C_1 \times V_1 \\ &= 3 \times 10^{-6} \times 8 \\ &= 24 \times 10^{-6} \\ &= 24 \ \mathrm{[\mu C]} \\[10pt] Q_2 &= C_2 \times V_2 \\ &= 6 \times 10^{-6} \times 4 \\ &= 24 \times 10^{-6} \\ &= 24 \ \mathrm{[\mu C]} \end{aligned} \]したがって、両方のコンデンサに蓄えられる電荷は24μCで同じです。これは直列接続では電荷が同じになるという理論と一致します。
完璧や!計算も考え方も完全に理解できてるな!
直列接続のコンデンサでは電荷が同じになるっていう重要なポイントも確認できたな。今回の練習問題では、両方のコンデンサに24μCの電荷が蓄えられることが分かったわけや。
まとめると、コンデンサの問題では次のことを覚えておくとええで:
- 並列接続: C = C1 + C2 (静電容量は足し算)
- 直列接続: C = (C1 × C2) / (C1 + C2) (抵抗の並列と同じ形)
- 並列接続: 電圧は同じ、電荷は分配される
- 直列接続: 電荷は同じ、電圧は分配される(静電容量に反比例)
- 基本公式: Q = C × V
これらをしっかり覚えておけば、第三種電気主任技術者試験のコンデンサの問題は解けるようになるで!
ありがとうございます、先生!コンデンサの並列接続と直列接続の特性がよく理解できました。要点をまとめていただいたので、とても分かりやすいです。試験でもこれらの知識をしっかり活用できるように復習します!
解説まとめ
スイッチを閉じる前後で、全体の電荷量は変化しません。したがって、次のように考えることができます。
図1の場合
コンデンサ\( C_1 \) および 、\( C_2 \)に蓄えられている電荷量 \( Q_1 \)は、
\( Q_1 = 2 + 4 = 6 \ \mathrm{[\mu C]} \)
このとき、図の上側が正極(+)となっています。
図2の場合
同様に、図2での蓄えられた電荷量 \( Q_2 \) は、
\( Q_2 = 4 - 2 = 2 \ \mathrm{[\mu C]} \)
ただし、図2では下側が正極(+)となります。
合成容量
2つのコンデンサの合成静電容量 \( C \) は、
\( C = C_1 + C_2 = 4 + 2 = 6 \ \mathrm{[\mu F]} \)
スイッチを閉じた後の電圧
スイッチを閉じたあとの各コンデンサの電圧は、以下のように求められます。
\( V_1 = \frac{Q_1}{C} = \frac{6 \times 10^{-6}}{6 \times 10^{-6}} = 1 \ \mathrm{[V]} \)
\( V_2 = \frac{Q_2}{C} = \frac{2 \times 10^{-6}}{6 \times 10^{-6}} = \frac{1}{3} \ \mathrm{[V]} \)
電圧比
最後に、2つの電圧の比は次のようになります。
\( \left| \frac{V_1}{V_2} \right| = \left| \frac{1}{\frac{1}{3}} \right| = 3 \)
したがって、電圧比は 3 となります。