【理論】令和6年 (下期) 問4|直流電流が流れる平行導体間に働く力の方向に関する論説問題
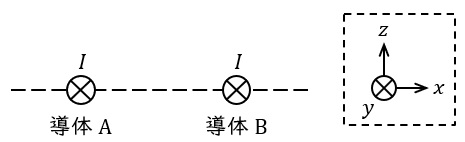
図に示すように,直線導体 \( \mathrm{A} \) および \( \mathrm{B} \) が \( y \) 方向に平行に配置され,両導体に同じ大きさの電流 \( I \) が共に \( +y \) 方向に流れているとする。
このとき,各導体に加わる力の方向について,正しいものを次の (1)~(5) のうちから一つ選べ。
なお,\( xyz \) 座標の定義は,破線の枠内の図で示したとおりとする。
\[ \begin{array}{cc} & \text{導体 A} \quad \text{導体 B} \\ \hline (1) & +x \text{ 方向} \quad +x \text{ 方向} \\ \hline (2) & +x \text{ 方向} \quad -x \text{ 方向} \\ \hline (3) & -x \text{ 方向} \quad +x \text{ 方向} \\ \hline (4) & -x \text{ 方向} \quad -x \text{ 方向} \\ \hline (5) & \text{どちらの導体にも力は働かない} \\ \hline \end{array} \]
合格への方程式
電流と磁場の基本関係
電流が作る磁場
電流が流れる導体の周りには磁場が発生します。この現象は1820年にエルステッドによって発見され、電気と磁気の関係を明らかにした歴史的な発見です。身近な例では、電磁石やモーターがこの原理を利用しています。
アンペールの法則(直線導体)
無限に長い直線導体に電流 I が流れるとき、導体から距離 r の点での磁場の強さ H は:
\[ H = \frac{I}{2\pi r} \]ここで:
- \( H \):磁場の強さ [A/m]
- \( I \):電流 [A]
- \( r \):導体からの距離 [m]
磁場の方向(右手の法則)
電流が作る磁場の方向は右手の法則で決まります。
右手の法則の使い方
- 右手の親指を電流の方向に向ける
- 残りの4本の指が巻きつく方向が磁場の方向
- 磁場は導体を中心とした同心円状に分布
磁場と磁束密度の関係
磁場の強さ H と磁束密度 B の間には、媒質の透磁率 μ を介して以下の関係があります:
\[ B = \mu H \]真空中では:
\[ B = \mu_0 H = \frac{\mu_0 I}{2\pi r} \]ここで \( \mu_0 = 4\pi \times 10^{-7} \, \mathrm{H/m} \) は真空の透磁率です。
単位の整理
- 磁場の強さ H:[A/m](アンペア毎メートル)
- 磁束密度 B:[T](テスラ)または [Wb/m²]
- 透磁率 μ:[H/m](ヘンリー毎メートル)
距離による磁場の変化
直線導体の磁場は距離に反比例します。これは重要な特徴です。
距離と磁場の関係
電流10Aが流れる導体の場合:
- 1m地点:\( H = \frac{10}{2\pi \times 1} = 1.59 \, \mathrm{A/m} \)
- 2m地点:\( H = \frac{10}{2\pi \times 2} = 0.80 \, \mathrm{A/m} \)(半分)
- 10m地点:\( H = \frac{10}{2\pi \times 10} = 0.16 \, \mathrm{A/m} \)(1/10)
重ね合わせの原理
複数の電流がある場合、各電流による磁場をベクトル的に加算します。
同方向電流の場合
2本の平行導体に同方向の電流が流れる場合:
- 導体間の領域では磁場が弱くなる
- 導体外側の領域では磁場が強くなる
反対方向電流の場合
2本の平行導体に反対方向の電流が流れる場合:
- 導体間の領域では磁場が強くなる
- 導体外側の領域では磁場が弱くなる
実用的な応用例
電流による磁場の主要応用
→ 横スクロールして下さい →
| 応用分野 | 具体例 | 原理の活用方法 |
|---|---|---|
| 電動機・発電機 | 誘導電動機、同期発電機 | 導体電流による回転磁場生成 |
| 変圧器 | 配電用変圧器、電源トランス | 一次電流による磁束生成 |
| 計測器 | 電流計、磁場センサ | 電流による磁場を利用した測定 |
| 電磁石 | リレー、ソレノイド、MRI | コイル電流による強磁場生成 |
| 送電線路 | 高圧送電線、配電線 | 線路電流による磁場の影響評価 |
磁場の測定方法
1. ガウスメーター
ホール素子を利用した磁束密度の直接測定:
- 高精度測定が可能
- DC~低周波対応
- 小型で取り扱いが容易
2. フラックスゲート磁力計
地磁気レベルの微弱磁場測定用:
- 極めて高感度
- 方向も同時測定
- 研究・調査用途
3. サーチコイル
変動磁場の測定:
- ファラデーの法則を利用
- 交流磁場専用
- 広帯域測定が可能
安全性への配慮
磁場による健康影響
強い磁場は人体に影響を与える可能性があります:
- ペースメーカー:数mT以上で誤動作の可能性
- 磁気カード:数十mTで情報消失
- 精密機器:CRTディスプレイや計測器への影響
電力設備での配慮
大電流が流れる電力設備では:
- 作業者の安全確保:磁場強度の事前計算
- 機器配置の最適化:相互干渉の回避
- シールド設計:必要に応じた磁気遮蔽
計算上の近似と実際
理論と実際の違い
- 無限長導体の仮定:実際は有限長だが、長さが距離より十分大きければ近似可能
- 導体の太さ:理論では線電流、実際は有限の太さを持つ
- 周囲環境の影響:鉄構造物による磁場の歪み
- 温度・周波数特性:導体抵抗や透磁率の変化
これらの基本原理を理解することで、平行導体間の相互作用も正確に解析できるようになります。
平行導体間の相互作用
相互作用の基本メカニズム
2本の平行導体に電流が流れるとき、一方の導体が作る磁場が他方の導体に流れる電流と相互作用して力が発生します。この現象は電磁力の基本的な現れ方の一つです。
相互作用の原理
- 導体Aの電流 → 磁場を生成
- 導体Bの電流 → 導体Aの磁場中で力を受ける
- 作用・反作用の法則により、導体Aも同じ大きさの逆向きの力を受ける
同方向電流の場合(引力)
両導体に同じ方向の電流が流れる場合、導体間には引力が働きます。
磁場の分布
同方向電流による磁場の特徴:
- 導体間の領域:2つの磁場が逆向きで弱くなる
- 導体外側の領域:2つの磁場が同向きで強くなる
- 磁力線の密度差により導体間に引力が発生
身近な例:送電線
送電線では、隣接する相導体間で引力が働きます:
- 通常時:設計上考慮された範囲内
- 短絡時:大電流により強大な引力が発生
- 対策:適切な支持構造物の設計が必要
反対方向電流の場合(斥力)
両導体に反対方向の電流が流れる場合、導体間には斥力が働きます。
磁場の分布
反対方向電流による磁場の特徴:
- 導体間の領域:2つの磁場が同向きで強くなる
- 導体外側の領域:2つの磁場が逆向きで弱くなる
- 磁力線の密度差により導体間に斥力が発生
力の大きさの計算
平行導体間に働く力の大きさは以下の式で求められます:
平行導体間の力(単位長さあたり)
\[ F = \frac{\mu I_1 I_2}{2\pi r} \]ここで:
- \( F \):単位長さあたりの力 [N/m]
- \( \mu \):透磁率 [H/m]
- \( I_1, I_2 \):各導体の電流 [A]
- \( r \):導体間の距離 [m]
導出過程
力の式の導出手順:
ステップ1:磁束密度の計算
導体1による導体2の位置での磁束密度:
\[ B_1 = \frac{\mu I_1}{2\pi r} \]ステップ2:力の計算
導体2(電流 \( I_2 \))が磁場 \( B_1 \) 中で受ける力:
\[ F = B_1 \times I_2 = \frac{\mu I_1 I_2}{2\pi r} \]実際の計算例
計算例
条件:
- 導体間距離:r = 0.5 m
- 電流:I₁ = I₂ = 1000 A
- 媒質:空気(μ = μ₀)
計算:
\[ \begin{aligned} F &= \frac{\mu_0 I_1 I_2}{2\pi r} \\[10pt] &= \frac{4\pi \times 10^{-7} \times 1000 \times 1000}{2\pi \times 0.5} \\[10pt] &= \frac{4 \times 10^{-4}}{1} \\[10pt] &= 0.4 \, \mathrm{N/m} \end{aligned} \]結果:単位長さあたり 0.4 N の力が働く
力の特性
1. 電流の積に比例
力は両導体の電流の積に比例します:
- 一方の電流が2倍 → 力も2倍
- 両方の電流が2倍 → 力は4倍
- 短絡事故時に巨大な力が発生する理由
2. 距離に反比例
力は導体間距離に反比例します:
- 距離が半分 → 力は2倍
- 距離が1/10 → 力は10倍
- 近接配置ほど大きな力が働く
3. 透磁率に比例
周囲の媒質によって力が変化:
- 空気中:μ ≈ μ₀
- 鉄心近傍:μ >> μ₀(力が大幅に増加)
電力システムへの影響
正常運転時
通常の運転電流による影響:
三相送電線の場合
- 相間力:隣接相間で引力・斥力が交番
- 機械的応力:導体やがいしに周期的な力
- 振動:風との相互作用で共振の可能性
異常時(短絡・地絡)
事故時の大電流による影響:
事故時の電磁力
- 巨大な瞬間力:通常の100倍以上も可能
- 機械的破壊:導体の変形、支持物の破損
- 設備損傷:開閉装置の接触部分離
- 安全対策:高速保護リレーによる早期遮断
設計上の考慮事項
1. 導体配置
電磁力を考慮した最適配置:
- 適切な相間距離:電磁力と絶縁性能のバランス
- 対称配置:不平衡力の最小化
- 支持点間隔:機械的強度の確保
2. 支持構造
電磁力に耐える構造設計:
- がいし強度:引張・圧縮・曲げ応力に対応
- 支持金具:繰り返し応力への耐久性
- 基礎構造:全体的な安定性の確保
測定と評価
理論計算の検証
実際の力の測定方法:
実験セットアップ
- 力センサー:ロードセルによる直接測定
- 変位測定:レーザー干渉計による微小変位観測
- ひずみゲージ:導体の機械的応力測定
- 高速カメラ:短絡時の動的挙動観察
シミュレーション
有限要素法による解析:
- 3次元磁場解析:複雑な形状での磁場分布
- 構造解析:機械的応力・変形の評価
- 連成解析:電磁場と構造の相互作用
実用的な応用例
平行導体の電磁力を利用した技術
→ 横スクロールして下さい →
| 技術分野 | 応用例 | 力の利用方法 |
|---|---|---|
| 電磁ブレーキ | 電車、エレベーター | 渦電流による制動力 |
| 電磁アクチュエータ | リニアモーター、ソレノイド | 導体間力による駆動 |
| 電磁成形 | 金属加工 | 高電流パルスによる成形力 |
| 計測器 | 電流計、力計 | 電流比例力の測定利用 |
| 核融合装置 | トカマク、ステラレータ | プラズマ閉じ込めコイルの支持 |
このような電磁力の理解は、電力機器の設計から先端技術の開発まで、幅広い分野で重要な基礎知識となります。
フレミングの法則応用
フレミングの左手の法則
フレミングの左手の法則は、電流、磁場、力の相互関係を表す重要な法則です。磁場中に置かれた電流が流れる導体に働く力の方向を決定します。
フレミングの左手の法則
左手の3本の指を互いに垂直にして:
- 人差し指:磁場(磁束密度 B)の方向
- 中指:電流(I)の方向
- 親指:力(F)の方向
数式で表すと:
\[ \vec{F} = I \vec{l} \times \vec{B} \]ここで \( \vec{l} \) は電流方向の単位ベクトルです。
力の大きさの計算
磁場中の電流に働く力の大きさは以下の式で計算されます:
\[ F = B I l \sin\theta \]ここで:
- \( F \):力の大きさ [N]
- \( B \):磁束密度 [T]
- \( I \):電流 [A]
- \( l \):導体の長さ [m]
- \( \theta \):電流と磁場のなす角
特別な場合
- 電流と磁場が垂直(θ = 90°):\( F = BIl \)(最大)
- 電流と磁場が平行(θ = 0°):\( F = 0 \)(力なし)
- 一般的な問題:垂直の場合が多い
平行導体問題への適用
平行導体間の力を求める際のフレミングの法則の適用手順:
ステップ1:磁場の方向決定
一方の導体による他方の導体位置での磁場方向を求める:
導体Aによる導体B位置での磁場
- 右手の法則で導体Aの電流による磁場方向を決定
- 導体Bの位置での磁場方向を特定
- 本問の場合:導体A(+y方向電流)により、導体B位置では-z方向の磁場
ステップ2:電流方向の確認
力を受ける導体(導体B)の電流方向:
- 本問の場合:導体Bの電流は+y方向
ステップ3:力の方向決定
フレミングの左手の法則を適用:
導体Bに働く力の方向
- 人差し指:磁場方向(-z方向)
- 中指:電流方向(+y方向)
- 親指:力の方向(-x方向)
同様に、導体Aに働く力は+x方向となります。
ベクトル外積による計算
より厳密には、ベクトル外積を用いて力の方向を計算できます:
\[ \vec{F} = I \vec{l} \times \vec{B} \]具体的な計算例
本問の場合の計算:
導体Bに働く力
条件:
- 電流方向:\( \vec{l} = (0, 1, 0) \)(+y方向)
- 磁場方向:\( \vec{B} = (0, 0, -B) \)(-z方向)
外積計算:
\[ \vec{l} \times \vec{B} = (0, 1, 0) \times (0, 0, -B) = (-B, 0, 0) \]結果:力は-x方向(導体A側への引力)
座標系との関係
問題では座標系が定義されているため、それに基づいて方向を判断する必要があります。
座標系の確認
- x軸:導体間の方向
- y軸:電流の方向
- z軸:右手座標系で決まる方向
右手座標系の確認
座標系の整合性確認:
- 右手の親指をx軸正方向に向ける
- 人差し指をy軸正方向に向ける
- 中指がz軸正方向を示す
実際の問題解法手順
標準解法手順
- 座標系の確認:x, y, z軸の定義を理解
- 電流方向の確認:各導体の電流方向
- 磁場方向の決定:右手の法則で各導体が作る磁場
- 力の方向計算:フレミングの左手の法則を適用
- 結果の検証:物理的妥当性の確認
よくある間違いとその対策
1. 座標軸の混同
よくある間違い
- 問題図の座標系を正しく読み取れない
- 右手座標系と左手座標系を混同
- 軸の正負を逆に理解
対策
- 問題図の座標系定義を最初に確認
- 右手を使って座標系の整合性をチェック
- 各軸の正方向を明確に把握
2. 法則の適用ミス
よくある間違い
- 右手の法則と左手の法則を混同
- 指の対応を間違える
- 磁場と電流の方向を逆に理解
対策
- 右手の法則:電流→磁場
- 左手の法則:磁場+電流→力
- 毎回指を使って確認する習慣をつける
記憶法と実践的コツ
フレミングの法則の覚え方
効果的な記憶法:
語呂合わせ
- 左手の法則:「電(でん)・磁(じ)・力(りき)」
- 人差し指:「電流」→実は「磁場」
- 中指:「磁場」→実は「電流」
- 親指:「力」
※注意:一般的な覚え方と指の対応が異なる場合があるので、自分に合った方法を確立することが重要
実践的な確認方法
- 図を描く:3次元的な関係を2次元図で表現
- 実際に手を使う:机上での理論確認
- 具体例で練習:身近な電気機器での確認
本問題への具体的適用
問題状況の整理
与えられた条件:
- 導体配置:AとBが平行(y方向)
- 電流方向:両導体とも+y方向
- 電流の大きさ:同じ(I)
- 求めるもの:各導体に働く力の方向
解法の実行
導体Bに働く力の計算
- 導体Aによる磁場:右手の法則で-z方向
- 導体Bの電流:+y方向
- フレミングの左手の法則:
- 人差し指:-z方向(磁場)
- 中指:+y方向(電流)
- 親指:-x方向(力)
- 結果:導体Bは-x方向に力を受ける
導体Aに働く力の計算
- 導体Bによる磁場:右手の法則で+z方向
- 導体Aの電流:+y方向
- フレミングの左手の法則:
- 人差し指:+z方向(磁場)
- 中指:+y方向(電流)
- 親指:+x方向(力)
- 結果:導体Aは+x方向に力を受ける
結果の検証
物理的妥当性の確認:
確認ポイント
- 同方向電流 → 引力(✓)
- 作用・反作用 → 両導体の力は逆向き(✓)
- 力の大きさ → 同じ電流なので同じ大きさ(✓)
最終答え
計算結果:
- 導体A:+x方向
- 導体B:-x方向
- 選択肢:(2)
答え:(2) 導体A:+x方向、導体B:-x方向
フレミングの法則は、電磁気学の最も基本的でありながら、最も実用的な法則の一つです。この問題を通じて、電磁力の基本的な理解を深めることができます。
🔍 ワンポイントアドバイス: 平行導体間の力の問題では、まず「同方向電流→引力」「反対方向電流→斥力」という基本原理で選択肢を絞り込みます。次に作用・反作用の法則により、両導体の力は大きさが等しく方向が逆になることを確認します。本問では同方向電流なので引力が働き、導体Aは+x方向、導体Bは-x方向の力を受けます。座標系の定義を正確に読み取り、右手の法則→左手の法則の順で段階的に解くことが確実な正解への近道です。
これはフレミングの左手の法則とアンペールの法則を組み合わせて考える問題やな。
まず電流の方向と座標系をしっかり確認していこか。
選択肢(1)から見ていこか。両方の導体が+x方向に力を受けるって考えはどうや?
しかし、同方向に電流が流れる平行導体は一般的に引き合う性質があるので、この選択肢は間違いだと考えます。
解説
正解は (2) です。
各選択肢の詳しい解説:
- 選択肢(1):両導体が+x方向に力を受ける → 反発を意味するが、同方向電流では引力が働くため誤り
- 選択肢(2):導体A(+x方向)、導体B(-x方向) → 互いに引き合う力を表し、同方向電流の性質と一致するため正解
- 選択肢(3):導体A(-x方向)、導体B(+x方向) → 反発を意味するため誤り
- 選択肢(4):両導体が-x方向に力を受ける → 作用・反作用の法則に反するため誤り
- 選択肢(5):力が働かない → 電流が流れる平行導体間には必ず力が働くため誤り
平行導体間に働く力は、電流の方向によって決まります。同方向電流では引力、反対方向電流では斥力が働きます。この問題では、フレミングの左手の法則とアンペールの法則を組み合わせて力の方向を求める基本的な応用問題です。
この問題のポイント
- 同方向に電流が流れる平行導体間には引力が働く
- 反対方向に電流が流れる平行導体間には斥力が働く
- 導体間に働く力は作用・反作用の関係にある
- 力の大きさは \( F = \frac{\mu I_a I_b}{2\pi r} \) で求められる