【理論】令和1年 問3｜磁化特性とヒステリシスループに関する穴埋め問題

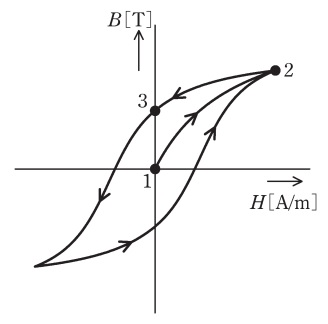
図は積層した電磁鋼板の鉄心の磁化特性（ヒステリシスループ）を示す。図中の \( B \) [T] および \( H \) [A/m] はそれぞれ磁束密度および磁界の強さを表す。

この鉄心にコイルを巻きリアクトルを製作し，商用交流電源に接続した。実効値が \( V \) [V] の電源電圧を印加すると，図中に矢印で示す軌跡が確認された。

コイル電流が最大のときの点は \( \fbox{（ア）} \) である。

次に，電源電圧実効値が一定に保たれたまま，周波数がやや低下したとき，ヒステリシスループの面積は \( \fbox{（イ）} \)。

一方，周波数が一定で，電源電圧実効値が低下したとき，ヒステリシスループの面積は \( \fbox{（ウ）} \)。

最後に，コイル電流実効値が一定で，周波数がやや低下したとき，ヒステリシスループの面積は \( \fbox{（エ）} \)。

回路図

→横スクロールしてください

\[ \begin{array}{ccccc} & （ア） & （イ） & （ウ） & （エ） \\ \hline (1) & 1 & \text{大きくなる} & \text{小さくなる} & \text{大きくなる} \\ \hline (2) & 2 & \text{大きくなる} & \text{小さくなる} & \text{あまり変わらない} \\ \hline (3) & 3 & \text{あまり変わらない} & \text{あまり変わらない} & \text{小さくなる} \\ \hline (4) & 2 & \text{小さくなる} & \text{大きくなる} & \text{あまり変わらない} \\ \hline (5) & 1 & \text{小さくなる} & \text{大きくなる} & \text{あまり変わらない} \\ \hline \end{array} \]

合格への方程式

ヒステリシスループの基本

ヒステリシスループとは？

定義：磁性体に磁界を加えたときの磁束密度B[T]と磁界の強さH[A/m]の関係をグラフにしたもので、特徴的な閉じたループを描きます。

形の特徴：磁界の強さを増加させていくときと減少させていくときで異なる経路をたどるため、履歴効果（ヒステリシス）と呼ばれます。

日常例で理解：磁石で鉄くぎを磁化した後、磁石を離しても鉄くぎが少し磁気を帯びたままになるのがヒステリシス現象です。

ヒステリシスループの重要な点

点1：残留磁束密度（Br）：磁界の強さがゼロでも残る磁束密度

点2：最大磁束密度：ループ上で磁束密度が最大となる点

点3：保磁力（Hc）：残留磁束を零にするのに必要な逆方向の磁界の強さ

試験ポイント：問題で「コイル電流が最大のとき」と聞かれたら、必ず点2（最大磁束密度の点）を選びましょう。

ヒステリシス損失

損失の発生：ヒステリシスループで囲まれた面積に比例して損失（ヒステリシス損）が発生します。

面積の意味：面積が大きいほど損失が大きく、面積が小さいほど損失が小さくなります。

実用上の重要性：変圧器や電動機の鉄心では、この損失を小さくするために珪素鋼板などの特殊な材料を使用します。

→　横スクロールして下さい　→

\[ \begin{aligned} P_h = k_h \times f \times B_{max}^n \quad [W/kg] \end{aligned} \]

意味：ヒステリシス損失の近似式。khは材料定数、fは周波数、Bmaxは最大磁束密度、nは1.6～2.0程度の指数です。

磁性体の種類と特性

軟磁性材料：

  • ヒステリシスループの面積が小さい
  • 電磁鋼板、パーマロイなど
  • 変圧器や電動機の鉄心に使用

硬磁性材料：

  • ヒステリシスループの面積が大きい
  • フェライト磁石、ネオジム磁石など
  • 永久磁石として使用

電磁気学の基礎法則

磁界と磁束密度の関係

真空中の関係：

→　横スクロールして下さい　→

\[ \begin{aligned} B = \mu_0 H \quad [T] \end{aligned} \]

ここで、μ₀ = 4π × 10⁻⁷ [H/m] は真空の透磁率です。

磁性体中の関係：

→　横スクロールして下さい　→

\[ \begin{aligned} B &= \mu H = \mu_0 \mu_r H \quad [T] \\[10pt] \mu &= \mu_0 \mu_r \quad [H/m] \end{aligned} \]

ここで、μは透磁率、μᵣは比透磁率です。

重要：磁性体では比透磁率μᵣが磁界の強さHによって変化するため、BとHは比例関係になりません。これがヒステリシス現象の原因です。

コイルと電流の関係

アンペアの法則：コイルに流れる電流Iと磁界の強さHは比例関係にあります。

→　横スクロールして下さい　→

\[ \begin{aligned} H = \frac{N \times I}{l} \quad [A/m] \end{aligned} \]

ここで、Nはコイルの巻数、Iは電流、lは磁路の長さです。

結論：電流I ∝ 磁界の強さH ∝ 磁束密度B（磁性体では近似的に）

試験での重要ポイント：コイル電流が最大 → 磁界の強さHが最大 → 磁束密度Bが最大

リアクトルの基本

リアクトルとは：インダクタンス成分を持つ受動素子。コイルに鉄心を入れたものが一般的です。

リアクタンスの計算：

→　横スクロールして下さい　→

\[ \begin{aligned} X_L &= \omega L = 2\pi f L \quad [\Omega] \\[10pt] I &= \frac{V}{X_L} = \frac{V}{2\pi f L} \quad [A] \end{aligned} \]

周波数との関係：

  • 周波数f↑ → リアクタンスXL↑ → 電流I↓
  • 周波数f↓ → リアクタンスXL↓ → 電流I↑

ファラデーの電磁誘導法則

誘導起電力：

→　横スクロールして下さい　→

\[ \begin{aligned} e = -N \frac{d\Phi}{dt} = -N \frac{d(BA)}{dt} \quad [V] \end{aligned} \]

正弦波交流での関係：

→　横スクロールして下さい　→

\[ \begin{aligned} V = 4.44 \times f \times N \times B_{max} \times A \quad [V] \end{aligned} \]

ここで、fは周波数、Nは巻数、Bmaxは最大磁束密度、Aは断面積です。

重要な関係：電圧V一定 → 周波数f↓なら → 最大磁束密度Bmax↑

問題解法のポイント

（ア）コイル電流が最大のときの点の判定

解法の手順：

  1. 電流I ∝ 磁界の強さH という関係を思い出す
  2. 磁性体では H ∝ B（近似的に）が成り立つ
  3. したがって、電流I ∝ 磁束密度B
  4. 電流が最大 = 磁束密度Bが最大の点を探す

判定のポイント：ヒステリシスループ上で磁束密度Bが最大となる点を見つけます。

間違いやすいポイント：残留磁束密度の点と混同しないよう注意しましょう。電流最大は必ず磁束密度最大の点です。

（イ）周波数低下時（電圧一定）の解法

解法の手順：

  1. XL = 2πfL なので、f↓ → XL↓
  2. I = V/XL なので、XL↓ → I↑
  3. I↑ → H↑ → B↑
  4. BとH両方が大きくなる → ループ面積の変化を判定

もう一つの考え方（誘導起電力から）：

V = 4.44fNBmaxA で、V一定、f↓ なら Bmax↑ という関係からも同じ結論が得られます。

（ウ）電圧低下時（周波数一定）の解法

解法の手順：

  1. 周波数一定 → XL = 2πfL は変わらず
  2. I = V/XL なので、V↓ → I↓
  3. I↓ → H↓ → B↓
  4. BとH両方が小さくなる → ループ面積の変化を判定

注意点：リアクタンスが変わらない状況での電圧変化なので、オームの法則がそのまま適用できます。

（エ）電流一定時（周波数低下）の解法

解法の手順：

  1. 電流I一定 → H = NI/l も一定
  2. H一定 → B もほぼ一定（磁性体の特性による）
  3. BとH両方がほぼ変わらず → ループ面積の変化を判定

重要ポイント：電流が一定に保たれている条件では、磁界も磁束密度もほぼ変化しないことを理解しましょう。

解答パターンの整理

ヒステリシスループ面積の変化要因：

  • 磁束密度Bが変化 → 面積も変化
  • 磁界の強さHが変化 → 面積も変化
  • BとH両方が同じ割合で変化 → 面積はその2乗に比例して変化

覚えるべき関係式：

  • XL = 2πfL （リアクタンス）
  • I = V/XL （オームの法則）
  • H ∝ I （アンペアの法則）
  • V = 4.44fNBmaxA （誘導起電力）

問題解法の基本戦略

Step1：条件の整理：

  • 何が一定で何が変化するかを明確にする
  • 電圧一定？電流一定？周波数一定？を確認

Step2：物理量の連鎖を追う：

  • 周波数f → リアクタンスXL → 電流I → 磁界H → 磁束密度B
  • 各段階で増加・減少・不変を判定

Step3：ループ面積への影響を判定：

  • BとHの変化からループの大きさの変化を推定
  • 大きくなる・小さくなる・あまり変わらないを選択

類似問題への対応

頻出パターン：

  • 周波数変化 + 電圧一定
  • 電圧変化 + 周波数一定
  • 電流一定 + 周波数変化
  • 温度変化による材料特性の変化

解法のコツ：まず「何が一定で何が変化するか」を整理してから、順番に関係式を適用していきましょう。物理量の因果関係を一つずつ丁寧に追うことが確実な解法への近道です。

🔍 ワンポイントアドバイス： ヒステリシスループ問題の攻略法は「電流→磁界→磁束密度→面積」の流れを確実に覚えることです。特に（ア）の「電流最大=磁束密度最大の点」は絶対に間違えてはいけない基本知識です。周波数や電圧が変化したときは、まずリアクタンスXL=2πfLがどう変わるかを考え、次にオームの法則I=V/XLで電流の変化を求めましょう。最後に「電流∝磁界∝磁束密度」の関係でループの大きさを判断します。この手順を身につければ、類似問題にも対応できます！

今日はヒステリシスループの問題や！

図を見ながら、磁化特性とコイル電流の関係を理解していこうな。

ヒステリシス損失も出てくるから、しっかり覚えとこうで！

解説

ヒステリシスループの問題は計算問題が出題されない分野です。真空中では\( B=\mu_0 H \)の関係が成立するとしていますが、磁性体ではこの関係は成立せず、磁界中で磁気を帯び磁化されます。磁化されることによって、ヒステリシスループで囲まれた面積に比例したヒステリシス損が発生します。

1.リアクトルのリアクタンス\( X_L \)

インダクタンスが\( L \mathrm{[H]} \)のリアクトル（コイル）のリアクタンス\( X_L \mathrm{[\Omega]} \)は、周波数を\( f \mathrm{[Hz]} \)、角周波数を\( \omega \mathrm{[rad/s]} \)とすると、

\[ X_L = j\omega L = j2\pi fL \mathrm{[\Omega]} \]

となります。

2.磁界と電流の関係

①基本的な比例関係

②ヒステリシスループの面積

3.各空欄の解説

(ア) 磁界の強さ\( H \)は電流\( I \)に比例し、磁束密度\( B \)は磁界の強さ\( H \)に比例します。したがって、コイル電流が最大となるのは磁束密度及び磁界の強さが最大となる点2となります。

(イ) 周波数が低下するとコイルのリアクタンス\( X_L = 2\pi fL \)が低下するので、コイル電流が増加し、磁界の強さ\( H \)及び磁束密度\( B \)が大きくなります。したがって、ヒステリシスループの面積は大きくなります。

(ウ) 周波数が変わらないので、リアクタンスの大きさが変わりません。この状況で電源電圧が低下すると、オームの法則によりコイル電流は減少します。コイル電流が減少すると、磁界の強さ\( H \)及び磁束密度\( B \)は小さくなります。したがって、ヒステリシスループの面積は小さくなります。

(エ) コイル電流が変わらなければ、磁界の強さ\( H \)及び磁束密度\( B \)はあまり変わりません。したがって、ヒステリシスループの面積はあまり変わりません。

4.ヒステリシス損失の実用的意義

ヒステリシス損失は変圧器、モーター、発電機などの回転機において重要な損失成分です。効率向上のためには、ヒステリシス損失の少ない磁性材料の選択や、適切な動作点の設定が重要です。現代の電力機器では、方向性電磁鋼板やアモルファス合金などの低損失材料が使用され、エネルギー効率の向上が図られています。