【理論】令和6年 (下期) 問13|固定バイアス回路を用いたエミッタ接地トランジスタ増幅回路の抵抗値計算問題
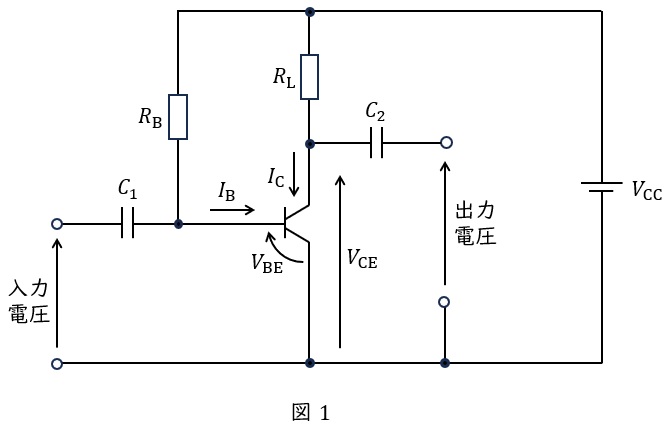
図1は,固定バイアス回路を用いた,\( R_{\mathrm{B}} \) の値が未知のエミッタ接地トランジスタ増幅回路である。
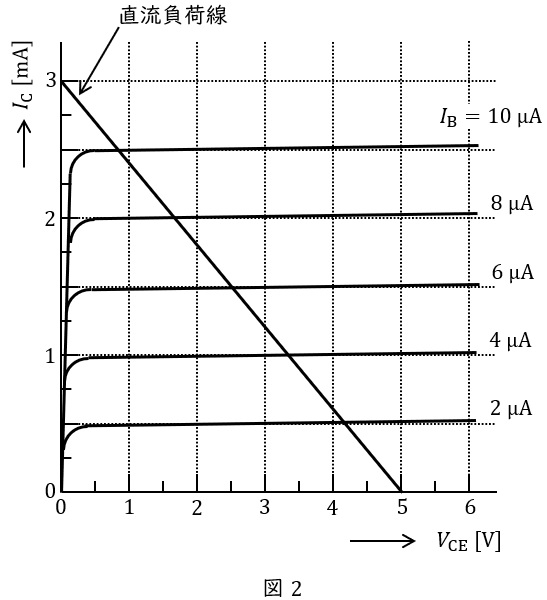
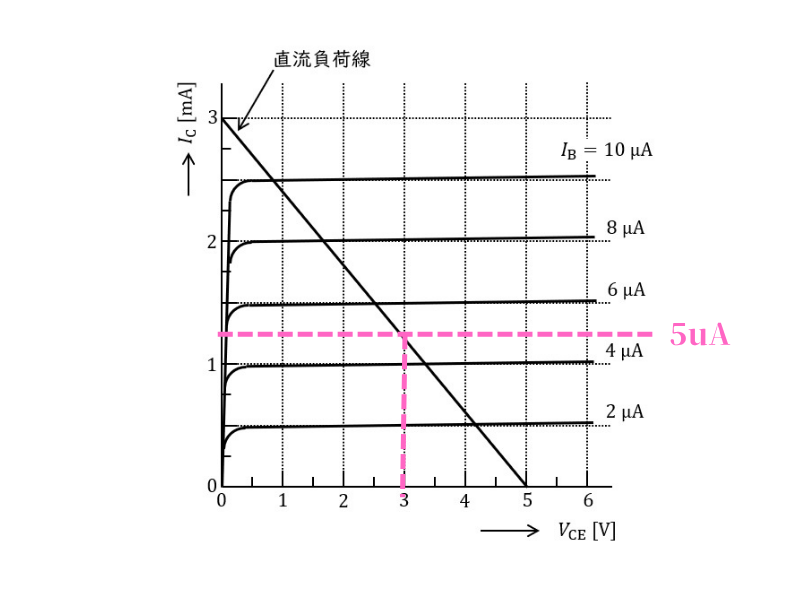
図2は,この増幅回路で用いているトランジスタのコレクタ-エミッタ間電圧 \( V_{\mathrm{CE}} \) とコレクタ電流 \( I_{\mathrm{C}} \) との関係を予め調べ示した静特性である。
ただし,五つのベース電流の値 \( I_{\mathrm{B}} \) [\( \mu \mathrm{A} \)] のみに対する曲線であり,増幅回路の負荷抵抗 \( R_{\mathrm{L}} \) の負荷線も重ねて示している。
今,増幅回路の動作点を測定したところ \( V_{\mathrm{CE}} = 3.0 \) [V] であった。
抵抗 \( R_{\mathrm{B}} \) の値 [\( \mathrm{M\Omega} \)] として最も近いものを次の (1) ~ (5) のうちから一つ選べ。
ただし,ベース-エミッタ間電圧 \( V_{\mathrm{BE}} \) を \( 0.7 \) [V] としてよい。
なお,\( C_1 \),\( C_2 \) は結合コンデンサであり,\( V_{\mathrm{CC}} \) は直流電圧源である。
合格への方程式
固定バイアス回路の基礎理論

回路構成と各素子の役割
固定バイアス回路は、トランジスタ増幅回路の最も基本的な形式です。この回路は以下の主要素子で構成されています:
主要素子とその役割
- トランジスタ(NPN型): 信号を増幅する能動素子
- バイアス抵抗 \( R_B \): ベース電流を制限し、動作点を設定
- 負荷抵抗 \( R_L \): コレクタ電流を制限し、出力電圧を決定
- 結合コンデンサ \( C_1, C_2 \): 直流成分をカットし、交流信号のみを通す
- 電源電圧 \( V_{CC} \): 回路に動作電力を供給
トランジスタの基本動作原理
NPNトランジスタは3つの端子(ベース、エミッタ、コレクタ)を持つ半導体素子です。その動作は「水道の蛇口」に例えることができます:
水道の蛇口に例えた動作原理
- ベース: 蛇口のハンドル(わずかな力で大きな水流を制御)
- エミッタ: 水の入口
- コレクタ: 水の出口
ベースに小さな電流を流すことで、エミッタ-コレクタ間に大きな電流を流すことができます。これが「電流増幅」の原理です。
キルヒホッフの法則の適用
この回路の解析では、キルヒホッフの電圧法則(KVL)が重要な役割を果たします。閉回路内の電圧降下の総和は零になるという法則です。
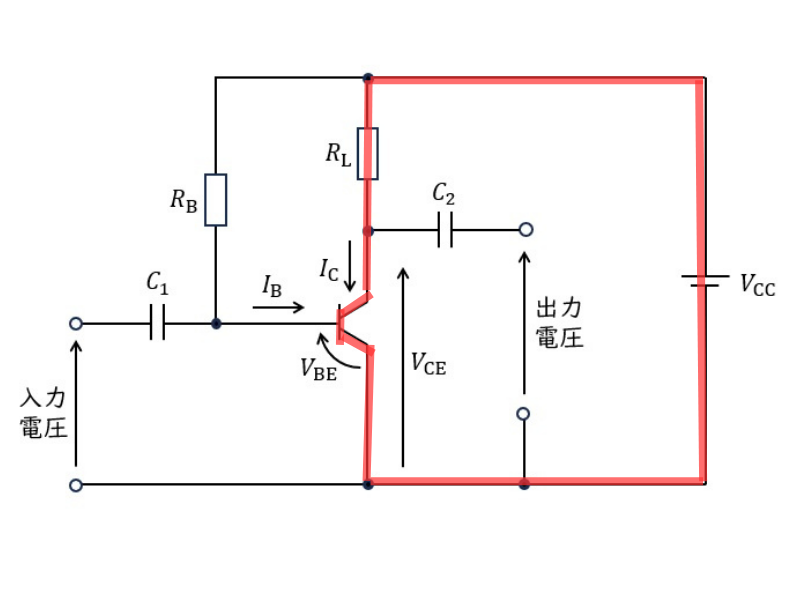
コレクタ回路での電圧関係
コレクタ回路(\( V_{CC} \) → \( R_L \) → トランジスタ → 接地)について:
\[ V_{CC} = V_{CE} + R_L I_C \]この式は、電源電圧が負荷抵抗での電圧降下とトランジスタのコレクタ-エミッタ間電圧に分配されることを示しています。
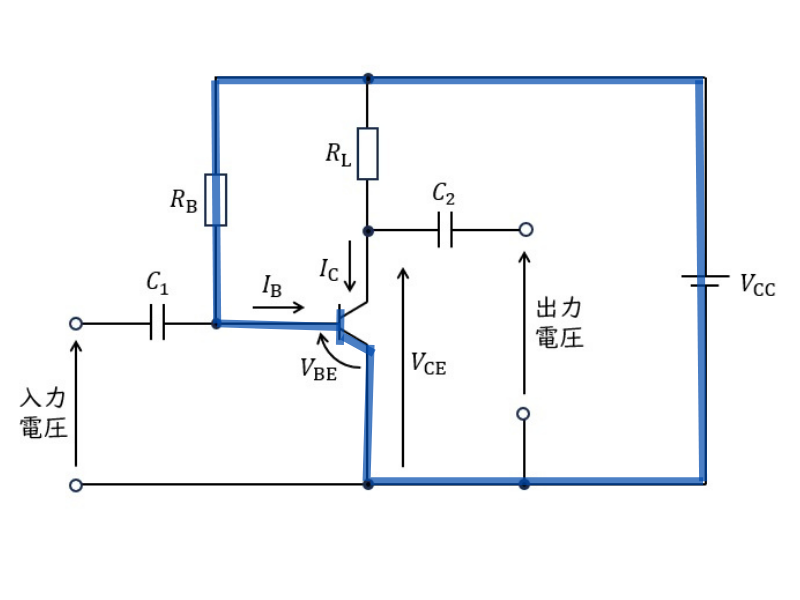
ベース回路での電圧関係
ベース回路(\( V_{CC} \) → \( R_B \) → ベース-エミッタ接合 → 接地)について:
\[ V_{CC} = R_B I_B + V_{BE} \]この式は、電源電圧がバイアス抵抗での電圧降下とベース-エミッタ間電圧(通常0.7V)に分配されることを示しています。
固定バイアス回路の特徴
固定バイアス回路の長所と短所
長所:
- 回路構成が非常に簡単
- 部品点数が少ない
- 解析が容易
短所:
- 温度変化に対する安定性が悪い
- トランジスタの個体差の影響を受けやすい
- 実用回路としては使用されることが少ない
トランジスタ静特性の読み方と活用

静特性とは何か
静特性(Static Characteristics)とは、トランジスタに直流電圧・電流を加えたときの電気的特性を表すグラフです。これは「トランジスタの性格を表す身分証明書」のようなものです。
静特性の基本的な見方
- 横軸: コレクタ-エミッタ間電圧 \( V_{CE} \) [V]
- 縦軸: コレクタ電流 \( I_C \) [mA]
- パラメータ: ベース電流 \( I_B \) [μA]の値
静特性の領域分析
静特性には主に3つの動作領域があります:
| 動作領域 | 特徴 | 用途 | 電圧・電流の状態 |
|---|---|---|---|
| 飽和領域 | \( V_{CE} \)が小さい(約0.2V以下) | スイッチング回路のON状態 | \( I_C \)が最大、\( V_{CE} \)≈ 0 |
| 活性領域 | \( I_C \)が\( I_B \)に比例 | 増幅回路の動作点 | 線形な電流増幅が可能 |
| 遮断領域 | \( I_B \) = 0、\( I_C \) ≈ 0 | スイッチング回路のOFF状態 | \( V_{CE} \)≈ \( V_{CC} \) |
負荷線の概念と読み方
負荷線(Load Line)は、回路の制約条件を静特性上に表したものです。これは「回路が許可する動作範囲」を示します。
負荷線の決定方法
負荷線は以下の2点を結んだ直線です:
- X切片: \( I_C = 0 \)のとき、\( V_{CE} = V_{CC} \)
- Y切片: \( V_{CE} = 0 \)のとき、\( I_C = V_{CC}/R_L \)
問題では、\( I_C = 0 \)で \( V_{CE} = 5.0V \)なので、\( V_{CC} = 5.0V \)と分かります。
動作点の読み取り
動作点(Operating Point)は、負荷線と特定の\( I_B \)曲線の交点で決まります。
動作点の意味
動作点は「信号が入力されていない状態(無信号時)でのトランジスタの電圧・電流値」を表します。これは増幅回路の「基準点」となります。
- 問題では \( V_{CE} = 3.0V \) が測定値
- 静特性から \( I_B ≈ 5.0μA \) と読み取れる
- 対応する \( I_C \) の値も求まる
電流増幅率(hFE)の読み取り
静特性からトランジスタの電流増幅率も読み取ることができます:
\[ h_{FE} = \frac{I_C}{I_B} \]増幅率の計算例
\( V_{CE} = 3.0V \)、\( I_B = 5.0μA \)の動作点で、\( I_C = 1.0mA \)だとすると:
\[ h_{FE} = \frac{1.0 \times 10^{-3}}{5.0 \times 10^{-6}} = 200 \]この値は一般的なトランジスタの増幅率の範囲内です。
計算手順と解法テクニック
問題解決の基本ステップ
トランジスタ回路の解析は、以下の手順で系統的に進めることが重要です:
解析の基本手順
- 回路の理解: 回路構成と各素子の役割を把握
- 既知条件の整理: 与えられた値と求める値を明確化
- 静特性の読み取り: グラフから必要な値を正確に読み取り
- 電圧方程式の立式: キルヒホッフの法則を適用
- 計算の実行: 数値を代入して解を求める
- 解答の検証: 結果の妥当性を確認
ステップ1:電源電圧VCCの決定
まず、負荷線から電源電圧を求めます。負荷線は \( I_C = 0 \) で \( V_{CE} = V_{CC} \) となることを利用します。
VCCの計算
静特性の負荷線より:
- \( I_C = 0 \)のとき \( V_{CE} = 5.0V \)
- したがって \( V_{CC} = 5.0V \)
ステップ2:動作点でのベース電流の読み取り
測定された \( V_{CE} = 3.0V \) における \( I_B \) の値を静特性から読み取ります。
グラフの読み取りのコツ
- 負荷線と \( V_{CE} = 3.0V \) の交点を見つける
- その点がどの \( I_B \) 曲線上にあるかを確認
- 曲線の間にある場合は内挿して推定
- 問題では \( I_B ≈ 5.0μA \) と読み取れる
ステップ3:ベース回路の電圧方程式
ベース回路にキルヒホッフの電圧法則を適用します:
\[ V_{CC} = R_B I_B + V_{BE} \]VBEの標準値
シリコントランジスタのベース-エミッタ間電圧 \( V_{BE} \) は、通常約0.7Vです。これはPN接合の順方向電圧降下によるものです。
- シリコン: 約0.7V(一般的)
- ゲルマニウム: 約0.3V(古い素子)
ステップ4:RBの計算
電圧方程式を \( R_B \) について解きます:
\[ \begin{aligned} R_B &= \frac{V_{CC} - V_{BE}}{I_B} \\[10pt] &= \frac{5.0 - 0.7}{5.0 \times 10^{-6}} \\[10pt] &= \frac{4.3}{5.0 \times 10^{-6}} \\[10pt] &= 0.86 \times 10^6 \text{ [Ω]} \\[10pt] &= 0.86 \text{ [MΩ]} \end{aligned} \]計算上の注意点
よくある計算ミス
- 単位の間違い: μA(マイクロアンペア)= \( 10^{-6} \)A
- VBEの忘れ: ベース-エミッタ間電圧を考慮し忘れる
- グラフの読み取り誤差: 静特性からの値読み取りが不正確
- 有効数字: 測定値の精度に応じた有効数字での表現
検算と妥当性の確認
解答の検証
求めた \( R_B = 0.86 \text{MΩ} \) について:
- 選択肢 (2) 0.9MΩ に最も近い
- バイアス抵抗としては妥当な値の範囲(通常0.1~10MΩ)
- ベース電流 5μA は一般的な動作電流
類似問題への応用
この解法は他の固定バイアス回路問題にも応用できます:
応用のポイント
- 負荷抵抗 \( R_L \) が与えられている場合の解析
- 異なる動作点での計算
- 温度変化を考慮した解析
- AC解析への展開
応用・設計のポイントと発展
固定バイアス回路の実用性
固定バイアス回路は理論学習には最適ですが、実用回路としては限界があります。その理由と改善方法を理解することが重要です。
実用上の問題点
- 温度依存性: 温度上昇でトランジスタの特性が変化
- 個体差: 同型番でもトランジスタごとに特性がばらつく
- 電源電圧変動: 電源電圧の変化が動作点に直接影響
- 経年変化: 長期使用による特性劣化
改良型バイアス回路
実用的な増幅回路では、より安定なバイアス方式が使用されます:
| バイアス方式 | 特徴 | 安定性 | 回路複雑さ | 用途 |
|---|---|---|---|---|
| 固定バイアス | 最も簡単 | 悪い | 非常に簡単 | 理論学習用 |
| 電流帰還バイアス | エミッタ抵抗追加 | 良い | 簡単 | 一般的な増幅回路 |
| 電圧分割バイアス | ベース電圧を分圧で決定 | 非常に良い | やや複雑 | 高安定性が必要な回路 |
| 定電流バイアス | 電流源でバイアス | 極めて良い | 複雑 | IC内部回路 |
温度特性の影響
トランジスタの特性は温度に大きく依存します。これを理解することは実用設計で重要です。
主な温度依存性
- VBEの温度係数: 約-2mV/℃(温度上昇でVBEは減少)
- hFEの温度特性: 温度上昇で増加(約0.5~1%/℃)
- 漏れ電流の増加: 温度上昇で指数的に増加
温度変化の影響計算例
室温25℃から60℃に上昇した場合:
→ 横スクロールして下さい →
\[ \begin{aligned} \Delta T &= 60 - 25 = 35 \text{℃} \\[10pt] \Delta V_{BE} &= -2 \times 10^{-3} \times 35 = -0.07 \text{V} \\[10pt] V_{BE}(60℃) &= 0.7 - 0.07 = 0.63 \text{V} \end{aligned} \]この変化により、ベース電流とコレクタ電流が変化し、動作点がずれます。
設計指針と選定基準
実際の回路設計では、以下の指針に従います:
抵抗値選定の指針
- バイアス抵抗: ベース電流の10~100倍の電流が流れるよう選定
- 負荷抵抗: 所要の利得と出力電圧を考慮して決定
- 標準抵抗値: E12系列(10%, 5%)やE24系列(5%, 1%)を使用
- 電力定格: 消費電力の2~3倍の定格を選択
AC解析への発展
DC解析で動作点を求めた後は、AC解析で増幅特性を求めます:
AC解析のポイント
- 等価回路: トランジスタをハイブリッドパラメータ(hパラメータ)で表現
- 電圧利得: \( A_v = -h_{fe} \times \frac{R_L}{h_{ie}} \)
- 入力インピーダンス: \( Z_{in} = R_B \parallel h_{ie} \)
- 出力インピーダンス: \( Z_{out} ≈ R_L \)
発展的な解析手法
コンピュータシミュレーション
現代の回路設計では、SPICE系シミュレータが広く使用されています:
- SPICE: アナログ回路シミュレーションの標準
- LTspice: 無料で使える高機能シミュレータ
- Multisim: 教育用として普及
- TINA: 解析機能が豊富
現代的な応用分野
トランジスタ回路の基礎知識は、現代の電子技術でも重要です:
応用分野
- アナログIC設計: オペアンプ、コンパレータの内部回路
- 電源回路: レギュレータ、DC-DCコンバータ
- RF回路: 高周波増幅器、発振器
- センサ回路: 微小信号の増幅処理
- パワーエレクトロニクス: スイッチング素子の制御
学習を深めるための課題
- 異なる動作点での解析を試してみる
- 温度変化を考慮した特性変化を計算する
- 他のバイアス方式との比較検討を行う
- シミュレーションソフトで実際の回路動作を確認する
- 実際の回路を組んで測定してみる
🔍 ワンポイントアドバイス: 静特性の読み取りは「グラフの交点を正確に見つける」ことが重要です。負荷線と指定された電圧での垂直線の交点が、どのIB曲線上にあるかを慎重に確認しましょう。また、キルヒホッフの法則は「回路内の電圧降下の収支」を表すので、各素子での電圧降下を漏れなく考慮することがポイントです。実際の試験では、計算ミスを防ぐため、単位の換算(μA→A)に特に注意してください。
今度はトランジスタの問題やで!これは電子回路の基本中の基本やけど、電験三種でも出題される重要な分野や。
固定バイアス回路っていうのは、トランジスタを適切に動作させるための基本的な回路なんや。静特性のグラフを読み取りながら、未知の抵抗値を求める問題やな。

この回路で、動作点が \( V_{CE} = 3.0 \, \mathrm{V} \) になるときの \( R_B \) を求めるんや。まず、回路の構成を理解してみよう。
【回路構成の理解】
主要な構成要素:
・NPNトランジスタ(エミッタ接地増幅回路)
・ベースバイアス抵抗:\( R_B \)(未知、求めたい値)
・負荷抵抗:\( R_L \)
・結合コンデンサ:\( C_1 \), \( C_2 \)(交流成分のみ通す)
・電源電圧:\( V_{CC} \)
与えられた条件:
・動作点:\( V_{CE} = 3.0 \, \mathrm{V} \)
・ベース-エミッタ間電圧:\( V_{BE} = 0.7 \, \mathrm{V} \)(シリコントランジスタの標準値)
・静特性グラフが与えられている
解法の方針:
1. 静特性グラフから電源電圧 \( V_{CC} \) と負荷抵抗 \( R_L \) の関係を読み取る
2. 動作点から必要なベース電流 \( I_B \) を求める
3. キルヒホッフの法則でベースバイアス回路を解析
4. ベース抵抗 \( R_B \) を計算する
よし、回路の構成は理解できたな!そしたら静特性のグラフを見てみよう。

このグラフには負荷線も描かれてるんや。負荷線っていうのは、電源電圧と負荷抵抗で決まる直線で、トランジスタの動作点を決めるのに重要やで。まず、この負荷線から回路の基本パラメータを読み取ってみよう。
【静特性グラフの読み取り】
負荷線の特徴:
負荷線は直流負荷線と呼ばれ、以下の式で表されます:
→ 横スクロールして下さい →
\[ V_{CC} = V_{CE} + R_L I_C \]
グラフからの読み取り:
・\( I_C = 0 \, \mathrm{mA} \) のとき:\( V_{CE} = 5.0 \, \mathrm{V} \)
・\( V_{CE} = 0 \, \mathrm{V} \) のとき:\( I_C = 3.0 \, \mathrm{mA} \)
電源電圧の決定:
\( I_C = 0 \) のとき、\( V_{CE} = V_{CC} \) なので:
\[ V_{CC} = 5.0 \, \mathrm{V} \]【重要なポイント】
今回の問題では、\( R_B \) を求めるために電源電圧 \( V_{CC} = 5.0 \, \mathrm{V} \) を知る必要がありますが、負荷抵抗 \( R_L \) の具体的な値は計算に不要です。
よし!電源電圧が5Vって分かったな。そしたら次に、動作点での状態を詳しく見てみよう。
\( V_{CE} = 3.0 \, \mathrm{V} \) のときの動作点から、必要なベース電流を読み取るんや。これが重要なポイントやで!

【動作点の解析】
動作点の条件:
\( V_{CE} = 3.0 \, \mathrm{V} \) での動作
グラフからの読み取り:
負荷線と \( V_{CE} = 3.0 \, \mathrm{V} \) の交点を見ると:
・コレクタ電流:\( I_C \approx 1.2 \, \mathrm{mA} \)
・ベース電流:\( I_B \approx 5 \, \mathrm{\mu A} \)
【重要な発見】
動作点は \( I_B = 5 \, \mathrm{\mu A} \) の特性曲線上にあることが分かります。
これは、この動作点を実現するために、ベース回路には \( 5 \, \mathrm{\mu A} \) の電流を流す必要があることを意味します。
【次のステップ】
このベース電流 \( 5 \, \mathrm{\mu A} \) を実現するための \( R_B \) の値を計算します。
完璧や!動作点で \( I_B = 5 \, \mathrm{\mu A} \) が必要って分かったな。そしたら次に、ベース回路の解析をしてみよう。
ベース回路では、電源 \( V_{CC} \) からベース抵抗 \( R_B \) を通ってベース電流が流れるんや。キルヒホッフの法則を使って計算してみよか。

【ベース回路のキルヒホッフ解析】
ベース回路の構成:
電源 \( V_{CC} \) → ベース抵抗 \( R_B \) → ベース-エミッタ間(\( V_{BE} \))→ 接地
キルヒホッフの電圧法則:
回路の電圧降下の合計 = 電源電圧
\[ V_{CC} = R_B I_B + V_{BE} \]既知の値:
・\( V_{CC} = 5.0 \, \mathrm{V} \)(グラフから読み取り)
・\( I_B = 5.0 \, \mathrm{\mu A} = 5.0 \times 10^{-6} \, \mathrm{A} \)(動作点から)
・\( V_{BE} = 0.7 \, \mathrm{V} \)(問題で与えられた条件)
求める値:
\( R_B \)(ベースバイアス抵抗)
よし、キルヒホッフの式が立ったな!そしたら \( R_B \) について解いてみよう。
\( V_{CC} = R_B I_B + V_{BE} \) の式で、\( R_B \) 以外の値は全部分かってるから、簡単に計算できるで。数値を代入して計算してみよか!
【ベース抵抗の計算】
キルヒホッフの式:
\[ V_{CC} = R_B I_B + V_{BE} \]\( R_B \) について整理:
\[ R_B = \frac{V_{CC} - V_{BE}}{I_B} \]数値代入:
\[ \begin{aligned} R_B &= \frac{5.0 - 0.7}{5.0 \times 10^{-6}} \\[10pt] &= \frac{4.3}{5.0 \times 10^{-6}} \\[10pt] &= 0.86 \times 10^6 \, \mathrm{\Omega} \\[10pt] &= 0.86 \, \mathrm{M\Omega} \end{aligned} \]【計算結果】
\( R_B = 0.86 \, \mathrm{M\Omega} \)
【選択肢との照合】
計算結果 0.86MΩ に最も近い選択肢は (2) 0.9 です。
完璧や!答えは (2) 0.9MΩ やな。でも計算だけやなくて、この結果が妥当かどうかも確認してみよう。
トランジスタ回路では、ベース抵抗の値が適切な範囲にあるかどうかが重要やからな。0.86MΩっていう値は理論的に正しいかな?
【結果の妥当性確認】
1. オーダーの確認
・ベース抵抗:0.86MΩ(約1MΩ)
・ベース電流:5μA(マイクロアンペア)
・これらの値は一般的なトランジスタ回路の範囲内 ✓
2. 計算の検算
逆算による確認:
\[ \begin{aligned} I_B &= \frac{V_{CC} - V_{BE}}{R_B} \\[10pt] &= \frac{5.0 - 0.7}{0.86 \times 10^6} \\[10pt] &= \frac{4.3}{0.86 \times 10^6} \\[10pt] &= 5.0 \times 10^{-6} \, \mathrm{A} = 5 \, \mathrm{\mu A} ✓ \end{aligned} \]3. 実用的な観点
・MΩオーダーの抵抗は高抵抗だが、ベースバイアス回路では一般的
・ベース電流が小さいため、大きな抵抗値が必要
・電流増幅率(hFE)を考慮すると妥当な設計 ✓
よし、結果も妥当やな!そしたら他の選択肢がなんでダメなのかも確認してみよう。
どんな間違いをすると他の値になってしまうかを理解しておけば、同じミスを避けられるからな。
【他の選択肢の検討】
選択肢(1) 0.5MΩ:過小評価
もし \( R_B = 0.5 \, \mathrm{M\Omega} \) だと:
\( I_B = \frac{4.3}{0.5 \times 10^6} = 8.6 \, \mathrm{\mu A} \)
これは必要な5μAより大きすぎる。
選択肢(2) 0.9MΩ:正解
✓ 計算結果0.86MΩに最も近い
選択肢(3) 1.5MΩ:過大評価
もし \( R_B = 1.5 \, \mathrm{M\Omega} \) だと:
\( I_B = \frac{4.3}{1.5 \times 10^6} = 2.9 \, \mathrm{\mu A} \)
これは必要な5μAより小さすぎる。
選択肢(4) 3.0MΩ、(5) 6.0MΩ:大幅な過大評価
これらの値では、ベース電流が1~2μA程度になってしまい、所望の動作点を実現できない。
【よくある間違いパターン】
・静特性グラフの読み取りミス
・\( V_{BE} \) を考慮し忘れ
・単位の変換ミス(μA → A)
・キルヒホッフの式の立て方の間違い
よっしゃ!選択肢の検討もばっちりやな。そしたら、この問題で重要な「静特性の読み取り方」についてもう少し詳しく説明しとこう。
トランジスタの静特性は電子回路設計の基本やから、グラフの読み方をしっかり覚えといてや。
【静特性グラフの読み取り方法】
1. 軸の理解
・横軸:\( V_{CE} \)(コレクタ-エミッタ間電圧)
・縦軸:\( I_C \)(コレクタ電流)
・パラメータ:\( I_B \)(ベース電流)
2. 負荷線の意味
・直線の式:\( V_{CC} = V_{CE} + R_L I_C \)
・切片:(\( V_{CC} \), 0) と (0, \( \frac{V_{CC}}{R_L} \))
・実際の動作点は負荷線上にしか存在できない
3. 動作点の決定
・負荷線と特性曲線の交点が動作点
・バイアス条件により、どの \( I_B \) 曲線上で動作するかが決まる
・動作点から \( V_{CE} \), \( I_C \), \( I_B \) が同時に読み取れる
4. 設計への活用
・所望の動作点を実現するバイアス回路の設計
・温度変化や素子ばらつきの影響評価
・増幅特性や歪み特性の予測
ええ感じで静特性の理解も深まったな!そしたら最後に、この問題で学んだトランジスタ回路の知識を実際の電子回路でどう活かせるかも考えてみよう。
固定バイアス回路は電子回路の基本やから、いろんなところで使われてるんやで。どんな応用があると思う?
トランジスタの固定バイアス回路について学んで、電子回路の基本原理が理解できました。
特に印象的だったのは、静特性グラフから動作点を読み取り、それを実現するためのバイアス回路を設計するという考え方です。これは実際の回路設計でも重要なプロセスになりそうですね。
応用例としては、まずオーディオアンプが思い浮かびます。音声信号を増幅するために、トランジスタを適切な動作点で動作させる必要があり、そのためにバイアス回路が不可欠でしょう。
また、スイッチング回路でも、トランジスタをON/OFF動作させるために、適切なベース電流を供給する回路が必要になると思います。
センサー回路では、微小な信号を増幅する際に、ノイズの少ない動作点を設定することが重要で、今日学んだバイアス設計の知識が活かされそうです。
デジタル回路の前段増幅器や、電源回路の制御部分でも、トランジスタの適切なバイアス設定が信頼性に直結するのではないでしょうか。
素晴らしい理解やな!まさにその通りや。
特にオーディオアンプの話は鋭いで。音質を左右する重要な部分やからな。動作点がずれると音が歪んでしまうんや。だから高級オーディオでは、温度補償付きのバイアス回路を使ったりするんやで。
それからスイッチング回路も重要やな。最近のパワーエレクトロニクスでは、IGBTやMOSFETが主流やけど、基本的な考え方は今日学んだバイアス設計と同じや。
センサー回路での微小信号増幅も、まさに今日の知識が生きてくる分野やで。医療機器の心電図とか、工業計測の温度センサーとか、精密なバイアス設計が要求されるんや。
君の理解力なら、きっとアナログ回路設計も得意になるで〜
先生の具体例を聞いて、トランジスタ回路の応用の広さに驚きました!
高級オーディオでの温度補償付きバイアス回路というのは興味深いです。音質追求のために、ここまで精密な制御をしているとは思いませんでした。温度が変わってもバイアス点を一定に保つ技術なのでしょうね。
IGBTやMOSFETでも基本考え方が同じというのも勉強になります。デバイスは進歩しても、基本原理は変わらないということですね。
医療機器の心電図での応用は特に印象的です。人の命に関わる微小信号を正確に増幅するために、今日学んだような精密なバイアス設計が使われているとは。責任の重さを感じます。
工業計測での温度センサーも、製品の品質管理に直結する重要な部分ですね。今日の基礎知識が、こんなに重要な分野で活用されていることを知って、もっと深く勉強したくなりました。
電験三種の範囲を超えて、実際の設計まで学んでみたいと思います!
その意気やで!そういう探究心があれば絶対に上達するわ。そしたら最後に、この問題から派生して覚えておくべき「電験三種での関連知識」をまとめとこう。
トランジスタ以外にも、電子回路関連の問題は出るからな。今日の基礎を踏まえて、次に学ぶべき内容も整理しておこうや!
【電験三種での関連知識と発展内容】
【頻出パターン1:トランジスタ回路の基本】
・エミッタ接地、ベース接地、コレクタ接地の各増幅回路
・バイアス回路の種類(固定バイアス、自己バイアス、電圧分割バイアス)
・増幅度、入力・出力インピーダンスの計算
【頻出パターン2:オペアンプ回路】
・反転・非反転増幅回路
・加算器、減算器、積分器、微分器
・帰還回路と安定性
【頻出パターン3:デジタル回路】
・論理ゲート(AND, OR, NOT等)
・フリップフロップとカウンタ回路
・A/D、D/A変換器
【頻出パターン4:電力用半導体】
・ダイオード、サイリスタの特性
・インバータ回路の基本動作
・電力変換回路の効率計算
【解法の共通スキル】
1. 特性グラフの正確な読み取り
2. キルヒホッフの法則の適用
3. 等価回路による簡略化
4. 動作点解析と安定性評価
完璧や!ここまで理解できたら、トランジスタ回路の問題はもう怖くないやろ?
最後に今日学んだことをまとめて、次の学習ステップも示しとくわ。これで電験三種の電子回路分野がまた一歩前進やな!
【今日の学習成果と次のステップ】
【本日のポイント総復習】
1. 静特性グラフの読み取り:負荷線と特性曲線から動作点を決定
2. キルヒホッフ解析:ベース回路の電圧方程式による設計計算
3. バイアス回路設計:所望の動作点を実現する抵抗値の算出
4. 実用的応用:オーディオアンプ、センサー回路、スイッチング回路
5. 計算技術:単位変換とオーダー感覚の重要性
【次の学習ステップ】
・他のバイアス回路(自己バイアス、電圧分割バイアス)
・交流等価回路と小信号解析
・温度特性と安定性の考慮
・FETとMOSFETの基本特性
・オペアンプを使った実用回路
【継続学習のコツ】
・静特性グラフは必ず正確に読み取る
・キルヒホッフの法則を確実に適用する
・実際の回路との関連を常に意識する
・計算結果の妥当性を必ず確認する
【重要な解法パターン】
1. グラフから基本パラメータ読み取り → 2. 動作点決定 → 3. 回路方程式 → 4. 未知数算出
お疲れさまでした!トランジスタ回路をマスターして、電験三種合格に向けて着実に前進しましょう!
解説まとめ
問題回路図

■ トランジスタ固定バイアス回路とは
固定バイアス回路は、トランジスタ増幅回路において動作点を設定するための基本的な回路構成です。ベース抵抗RBを通じてベース電流IBを供給し、トランジスタの動作点を決定します。この回路は電子制御装置や信号処理回路において広く使用され、電気主任技術者にとって重要な回路解析技術の一つです。
トランジスタ静特性

■ 計算手順と公式
キルヒホッフの電圧法則(KVL)
閉回路における電圧降下の総和は電源電圧と等しくなります。
コレクタ回路:\( V_{CC} = V_{CE} + R_L I_C \)
ベース回路:\( V_{CC} = R_B I_B + V_{BE} \)
トランジスタの基本特性
トランジスタの動作は静特性曲線で表現されます。
ベース-エミッタ間電圧:\( V_{BE} = 0.7 \ \mathrm{V} \)(シリコントランジスタ)
電流増幅率:\( I_C = h_{FE} \times I_B \)
負荷線の方程式
負荷抵抗による制約条件を直線で表します。
\( I_C = \frac{V_{CC} - V_{CE}}{R_L} \)
動作点の決定
静特性曲線と負荷線の交点が動作点となります。
動作点:\( (V_{CE}, I_C, I_B) \)の組み合わせ
■ 具体的な計算例
問題条件
動作点での測定値:\( V_{CE} = 3.0 \ \mathrm{V} \)、ベース-エミッタ間電圧:\( V_{BE} = 0.7 \ \mathrm{V} \)、ベース抵抗:\( R_B \)(未知)
Step 1: 電源電圧VCCの決定
コレクタ回路の解析

コレクタ回路にキルヒホッフの電圧法則を適用します:
\[ \begin{aligned} V_{CC} &= V_{CE} + R_L I_C \end{aligned} \]負荷線から \( I_C = 0 \ \mathrm{mA} \) のとき \( V_{CE} = 5.0 \ \mathrm{V} \) であることが読み取れるので:
\[ \begin{aligned} V_{CC} &= 5.0 + R_L \times 0 \\[5pt] &= 5.0 \ \mathrm{V} \end{aligned} \]Step 2: 動作点でのベース電流の読み取り
動作点の特定

静特性から \( V_{CE} = 3.0 \ \mathrm{V} \) のときの \( I_B \) を読み取ります:
図2の静特性曲線より、\( V_{CE} = 3.0 \ \mathrm{V} \) において負荷線との交点は \( I_B ≒ 5.0 \ \mathrm{\mu A} \) の特性曲線上にあることがわかります。
\[ \begin{aligned} I_B &≒ 5.0 \ \mathrm{\mu A} = 5.0 \times 10^{-6} \ \mathrm{A} \end{aligned} \]Step 3: ベース抵抗RBの計算
ベース回路の解析

ベース回路にキルヒホッフの電圧法則を適用します:
\[ \begin{aligned} V_{CC} &= R_B I_B + V_{BE} \end{aligned} \]各値を代入して計算します:
\[ \begin{aligned} 5.0 &= R_B \times 5.0 \times 10^{-6} + 0.7 \\[5pt] R_B \times 5.0 \times 10^{-6} &= 5.0 - 0.7 \\[5pt] R_B \times 5.0 \times 10^{-6} &= 4.3 \\[5pt] R_B &= \frac{4.3}{5.0 \times 10^{-6}} \\[5pt] &= 0.86 \times 10^6 \ \mathrm{\Omega} \\[5pt] &= 0.86 \ \mathrm{M\Omega} \end{aligned} \]解析のポイント
静特性曲線から正確に動作点を読み取ることが重要です。\( V_{CE} = 3.0 \ \mathrm{V} \) での負荷線との交点が \( I_B = 5.0 \ \mathrm{\mu A} \) の特性曲線上にあることを確認する必要があります。
計算結果の整理
| パラメータ | 記号 | 値 | 単位 |
|---|---|---|---|
| 電源電圧 | \( V_{CC} \) | 5.0 | V |
| 動作点電圧 | \( V_{CE} \) | 3.0 | V |
| ベース電流 | \( I_B \) | 5.0 | μA |
| ベース抵抗 | \( R_B \) | 0.86 | MΩ |
結論:抵抗 \( R_B = 0.86 \ \mathrm{M\Omega} \) ≒ 0.9 MΩ 答え:(2)
■ 実務上の留意点
トランジスタ固定バイアス回路は、電子制御装置や計測機器において基本的な増幅回路として使用されます。特に電力系統の保護制御装置や監視装置において重要な技術です。
温度特性の考慮:トランジスタのVBEは温度により変化するため(約-2mV/℃)、実用回路では温度補償回路の併用を検討する必要があります。電源電圧変動の影響:固定バイアス回路は電源電圧変動に敏感なため、安定化電源の使用や電圧安定化回路の追加が重要です。トランジスタのばらつき:hFE(電流増幅率)は個体差が大きいため、量産時には選別や調整用可変抵抗の使用を検討します。
保護継電器への応用:電流・電圧検出回路において、測定レンジに応じた適切なバイアス設定により高精度な測定を実現できます。制御回路の設計:開閉装置の制御信号処理において、ノイズ耐性と応答速度を両立させるためのバイアス設計が重要です。絶縁設計:高電圧回路との絶縁を確保するため、光結合器やトランス結合との組み合わせを検討する必要があります。EMC対策:電磁ノイズによる誤動作を防ぐため、適切なフィルタ回路やシールド設計を併用することが重要です。