【理論】令和6年 (下期) 問7|直流電源を加えた抵抗の直並列回路における合成抵抗の計算問題
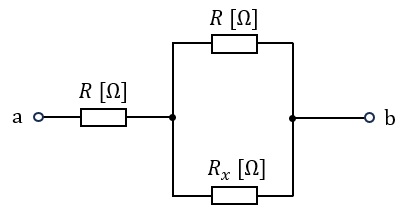
図の抵抗回路において,端子 \( \mathrm{a} \),\( \mathrm{b} \) 間の合成抵抗 \( R_{\mathrm{ab}} \) の値 \( [\Omega] \) は \( 1.8R \) [Ω] であった。
このとき,抵抗 \( R_x \) の値 \( [\Omega] \) として,正しいものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
問題と基本概念
今回の問題
図の抵抗回路において,端子 \( a \),\( b \) 間の合成抵抗 \( R_{\mathrm{ab}} \) の値 \( \mathrm{[\Omega]} \) は \( 1.8R \, \mathrm{[\Omega]} \) であった。このとき,抵抗 \( R_x \) の値 \( \mathrm{[\Omega]} \) として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( R \) (2) \( 2R \) (3) \( 3R \) (4) \( 4R \) (5) \( 5R \)

この問題のポイント
この問題は、既に分かっている抵抗 \( R \) と合成抵抗の値から、未知の抵抗 \( R_x \) を求める典型的な問題です。
重要なポイント
- 回路の構造をしっかり理解する
- どの部分が直列で、どの部分が並列かを見分ける
- 合成抵抗の公式を正しく使う
- 計算ミスをしないよう丁寧に計算する
回路の読み方
まず回路図を見て、電流の流れ方を考えましょう。端子 \( a \) から入った電流は:
- 最初に抵抗 \( R \) を通る(これは必ず通る道)
- その後、二手に分かれて抵抗 \( R \) と \( R_x \) に流れる(並列部分)
- 最後に合流して端子 \( b \) から出る
身近な例で考えてみよう
これは川の流れに似ています。川(電流)が最初は一本の道を通り、途中で二股に分かれ、最後にまた合流するようなイメージです。最初の一本道が直列部分、二股に分かれる部分が並列部分になります。
合成抵抗の公式と使い方
直列接続の合成抵抗
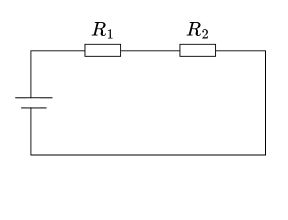
抵抗が一列に並んでいる(直列)場合、電流は必ずすべての抵抗を通ります。
直列の公式
\[ R = R_1 + R_2 + R_3 + \cdots \]つまり、足し算で求められます。
覚え方のコツ
直列は「まっすぐ列に並ぶ」→「足し算で合計」と覚えましょう。道路で考えると、信号が3つ連続であれば、全部の信号での待ち時間を足し合わせるのと同じです。
並列接続の合成抵抗
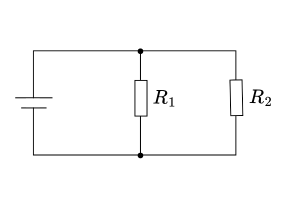
抵抗が並行に配置されている(並列)場合、電流は複数の道に分かれて流れます。
並列の公式
→ 横スクロールして下さい →
\[ \begin{aligned} \frac{1}{R} &= \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots \\[10pt] \text{2つの場合:} \quad R &= \frac{R_1 R_2}{R_1 + R_2} \end{aligned} \]覚え方のコツ
並列は「逆数の足し算」です。道路で考えると、複数の道があれば通りやすくなる(抵抗が小さくなる)のと同じです。
特別な場合の覚えておくと便利な公式
→ 横スクロールして下さい →
| 接続方法 | 条件 | 公式 |
|---|---|---|
| 並列 | 同じ抵抗値 \( R \) が \( n \) 個 | \( R_{\text{合}} = \frac{R}{n} \) |
| 並列 | 2つの抵抗が同じ値 \( R \) | \( R_{\text{合}} = \frac{R}{2} \) |
| 並列 | 一方が非常に小さい | 小さい方に近い値 |
計算例
抵抗値 \( 6\,\Omega \) と \( 3\,\Omega \) が並列接続されている場合:
\[ R = \frac{6 \times 3}{6 + 3} = \frac{18}{9} = 2\,\Omega \]元の抵抗より小さくなることに注目しましょう。
よくある間違い
- 並列で普通に足してしまう(直列の公式と混同)
- 逆数を取り忘れる
- 計算の途中で分数の計算を間違える
実際の解き方・計算手順
ステップ1:回路の構造を理解する
問題の回路は以下のような構造になっています:
- 端子 \( a \) から抵抗 \( R \) まで
- 抵抗 \( R \) の後で、上の枝の抵抗 \( R \) と下の枝の抵抗 \( R_x \) に分岐(並列部分)
- 並列部分が合流して端子 \( b \) へ
回路の見方のコツ
端子 \( a \) から \( b \) へ電流が流れる道筋を考えます。最初の \( R \) は必ず通る道なので直列、その後の \( R \) と \( R_x \) は選択できる道なので並列です。
ステップ2:並列部分の合成抵抗を求める
上の枝の抵抗 \( R \) と下の枝の抵抗 \( R_x \) が並列なので:
\[ R_{\text{並列}} = \frac{R \cdot R_x}{R + R_x} \]ステップ3:全体の合成抵抗を求める式を立てる
最初の抵抗 \( R \) と並列部分は直列なので:
\[ R_{\mathrm{ab}} = R + \frac{R \cdot R_x}{R + R_x} \]与えられた条件を代入
問題文より \( R_{\mathrm{ab}} = 1.8R \) なので:
\[ 1.8R = R + \frac{R \cdot R_x}{R + R_x} \]ステップ4:方程式を解いて \( R_x \) を求める
両辺から \( R \) を引いて:
\[ 0.8R = \frac{R \cdot R_x}{R + R_x} \]両辺に \( (R + R_x) \) をかけて:
→ 横スクロールして下さい →
\[ \begin{aligned} 0.8R(R + R_x) &= R \cdot R_x \\[10pt] 0.8R^2 + 0.8R \cdot R_x &= R \cdot R_x \\[10pt] 0.8R^2 &= R \cdot R_x - 0.8R \cdot R_x \\[10pt] 0.8R^2 &= 0.2R \cdot R_x \\[10pt] R_x &= \frac{0.8R^2}{0.2R} = 4R \end{aligned} \]検算してみよう
\( R_x = 4R \) を元の式に代入して確認:
\[ R_{\mathrm{ab}} = R + \frac{R \cdot 4R}{R + 4R} = R + \frac{4R^2}{5R} = R + 0.8R = 1.8R \,\checkmark \]正しく計算できました!
別解:代数の技法
最初から両辺を \( R \) で割って計算すると:
\[ 1.8 = 1 + \frac{R_x/R}{1 + R_x/R} \]\( R_x/R = k \) とおくと計算が簡単になります。
答え:(4) \( 4R \)
応用問題と発展的な考え方
類似問題のパターン
この種の問題は以下のようなバリエーションがあります:
パターン1:複数の未知抵抗
2つ以上の未知抵抗がある場合、複数の条件式が必要になります。
パターン2:異なる端子間の抵抗
端子の組み合わせを変えた場合の合成抵抗を求める問題もあります。
実際の回路での応用
このような計算は実際の電気回路設計でも重要です:
→ 横スクロールして下さい →
| 応用分野 | 具体例 | 重要性 |
|---|---|---|
| 電源回路 | 負荷抵抗の設計 | 適切な電流を流すため |
| フィルタ回路 | 周波数特性の調整 | ノイズ除去のため |
| 分圧回路 | 電圧の分割 | 必要な電圧を得るため |
| 測定回路 | 計器の内部抵抗 | 正確な測定のため |
より複雑な回路への発展
基本的な直列・並列の組み合わせから、さらに複雑な回路も解けるようになります:
ブリッジ回路
4つの抵抗が正方形状に配置され、対角線上に負荷がある回路です。平衡条件などの特別な解法が必要になります。
Δ-Y変換
三角形状(Δ)と星型(Y)の抵抗接続を相互変換する技法です。複雑な回路を簡単にできます。
問題を解くときの心構え
段階的なアプローチ
- 回路図をよく見る:どこが直列でどこが並列かを明確にする
- 簡単な部分から計算:まず分かりやすい部分の合成抵抗を求める
- 一歩ずつ合成:複雑な回路も段階的に合成していく
- 検算を忘れずに:最後に答えが条件を満たすか確認する
注意すべきポイント
- 回路図の読み間違い(特に交差点での接続の有無)
- 並列抵抗の計算での分数の取り扱い
- 単位の統一(\( \Omega \)、\( \mathrm{k\Omega} \)、\( \mathrm{M\Omega} \) など)
- 有効数字の処理
実習での確認方法
理論計算の結果は、実際に抵抗器を使った実験で確認できます:
- 計算値通りの抵抗器を用意
- ブレッドボードで回路を組む
- マルチメーターで合成抵抗を測定
- 理論値と実測値を比較
実験上の注意
実際の抵抗器には誤差があります(5%、1%など)。また、配線抵抗や接触抵抗も影響するため、理論値と完全に一致することは稀です。
🔍 ワンポイントアドバイス: 合成抵抗の問題は「回路の見方」が最も重要です。複雑に見える回路も、電流の流れる道筋を追って「直列」と「並列」に分けて考えれば、必ず解けます。計算ミスを防ぐため、途中の式も丁寧に書いて、最後は必ず検算しましょう。この基本がマスターできれば、より複雑な回路問題にも対応できるようになります。
まずは、この問題を一緒に見てみようか!回路図を見ながら、何が分かってて何を求めたいのかを整理してみよう。

端子 \( a \) と \( b \) の間の合成抵抗が \( 1.8R \, \mathrm{[\Omega]} \) やって分かってるんやな。そして、未知の抵抗 \( R_x \) を求めたいんや。どんな情報が見えるかな?
回路図を見ますと、端子 \( a \) と \( b \) の間に以下の構成があることが分かります:
・抵抗 \( R \) が1個直列に接続されている
・その後に、抵抗 \( R \) と \( R_x \) が並列に接続されている
つまり、\( R \) と「\( R \) と \( R_x \) の並列回路」が直列に接続された構成になっています。
与えられた条件:
・端子 \( a \), \( b \) 間の合成抵抗:\( R_{ab} = 1.8R \, \mathrm{[\Omega]} \)
・求めたい値:\( R_x \, \mathrm{[\Omega]} \)
よし、回路の構成が分かったな!そしたら次に、合成抵抗の基本を確認しとこか。直列と並列の合成抵抗の公式、覚えてるかな?


これらの公式、しっかり理解しておかんと後で困るで〜
合成抵抗の基本公式を確認いたします:
【直列合成抵抗】
抵抗 \( R_1 \) と \( R_2 \) が直列に接続されている場合:
\( R = R_1 + R_2 \)
電流の通り道が1つしかないので、抵抗値を単純に足し算します。
【並列合成抵抗】
抵抗 \( R_1 \) と \( R_2 \) が並列に接続されている場合:
→ 横スクロールして下さい →
\[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \]これを整理すると:
→ 横スクロールして下さい →
\[ R = \frac{R_1 R_2}{R_1 + R_2} \]並列接続では電流の通り道が複数あるため、全体の抵抗は各抵抗よりも小さくなります。
公式は大丈夫やな!じゃあ、この問題の回路をもう一回よ〜く見てみよか。
端子 \( a \) から端子 \( b \) に向かって、どういう順番で抵抗が繋がってるか分析してみよう。ここがポイントやで!
回路を端子 \( a \) から端子 \( b \) に向かって詳しく分析いたします:
【回路の構成分析】
1. 端子 \( a \) を出発点として、まず抵抗 \( R \) を通ります
2. その後、電流は2つの経路に分かれます:
・経路1:抵抗 \( R \) を通る
・経路2:抵抗 \( R_x \) を通る
3. 2つの経路は再び合流して端子 \( b \) に到達します
【回路の種類判定】
・最初の抵抗 \( R \) : 直列接続
・後半の抵抗 \( R \) と \( R_x \) : 並列接続
つまり、「直列の \( R \)」と「並列の \( R \) と \( R_x \)」が直列に接続された直並列回路です。
そうそう!直並列回路やな。そしたら計算の手順を考えてみよか。
まずは並列部分の合成抵抗を求めて、それから全体の合成抵抗を求めるんや。段階的にやっていけば絶対できるで!
まずは、\( R \) と \( R_x \) の並列合成抵抗を \( R_{\text{並}} \) として表してみよう。
並列部分の合成抵抗を求めます:
【ステップ1:並列合成抵抗の計算】
抵抗 \( R \) と \( R_x \) が並列接続されている部分の合成抵抗を \( R_{\text{並}} \) とします。
並列合成抵抗の公式を適用すると:
→ 横スクロールして下さい →
\[ R_{\text{並}} = \frac{R \cdot R_x}{R + R_x} \]【計算のポイント】
・分子:2つの抵抗値の積 \( R \times R_x \)
・分母:2つの抵抗値の和 \( R + R_x \)
この \( R_{\text{並}} \) が、後半部分を1つの抵抗として見たときの値になります。
よし!並列部分の式ができたな。そしたら次は、全体の合成抵抗を考えてみよう。
最初の \( R \) と、いま求めた \( R_{\text{並}} \) が直列に繋がってるってことやから、全体の合成抵抗 \( R_{ab} \) はどう表せるかな?
【ステップ2:全体の合成抵抗の表現】
回路全体は以下のような構成になっています:
・最初の抵抗:\( R \)
・後半の並列部分:\( R_{\text{並}} = \frac{R \cdot R_x}{R + R_x} \)
これらが直列に接続されているので、直列合成抵抗の公式を適用します:
→ 横スクロールして下さい →
\[ R_{ab} = R + R_{\text{並}} = R + \frac{R \cdot R_x}{R + R_x} \]【式の意味】
・第1項 \( R \):最初の直列抵抗
・第2項 \( \frac{R \cdot R_x}{R + R_x} \):並列部分の合成抵抗
この式が、端子 \( a \), \( b \) 間の合成抵抗の一般式です。
完璧や!そしたら、問題で与えられた条件を使って方程式を立ててみよう。
\( R_{ab} = 1.8R \) やったよな。これを使って \( R_x \) を求める方程式を作ってみよか。ここからが本番やで!
【ステップ3:方程式の設定】
問題の条件:\( R_{ab} = 1.8R \, \mathrm{[\Omega]} \)
前のステップで求めた式:\( R_{ab} = R + \frac{R \cdot R_x}{R + R_x} \)
これらを等しいとおくと:
→ 横スクロールして下さい →
\[ 1.8R = R + \frac{R \cdot R_x}{R + R_x} \]【方程式の整理の準備】
この方程式を \( R_x \) について解けば答えが求まります。
まずは左辺から右辺の \( R \) を移項して整理していきましょう。
よし、方程式ができたな!そしたら \( R_x \) について解いていこう。
まずは両辺から \( R \) を引いて、並列部分だけを残してみよか。計算ミスせんように注意深くやっていこな〜
【ステップ4:方程式の変形(第1段階)】
元の方程式:
→ 横スクロールして下さい →
\[ 1.8R = R + \frac{R \cdot R_x}{R + R_x} \]両辺から \( R \) を引きます:
→ 横スクロールして下さい →
\[ \begin{aligned} 1.8R - R &= \frac{R \cdot R_x}{R + R_x} \\[10pt] 0.8R &= \frac{R \cdot R_x}{R + R_x} \end{aligned} \]【変形のポイント】
・\( 1.8R - R = 0.8R \) となります
・これで並列部分の合成抵抗が \( 0.8R \) であることが分かりました
ええ感じや!\( 0.8R \) になったな。そしたら次は、分数を消すために両辺に \( (R + R_x) \) を掛けてみよう。
分数の計算が苦手な人も多いけど、ゆっくりやれば大丈夫やで!
【ステップ5:分数の消去】
現在の式:
→ 横スクロールして下さい →
\[ 0.8R = \frac{R \cdot R_x}{R + R_x} \]両辺に \( (R + R_x) \) を掛けます:
→ 横スクロールして下さい →
\[ \begin{aligned} 0.8R \times (R + R_x) &= \frac{R \cdot R_x}{R + R_x} \times (R + R_x) \\[10pt] 0.8R(R + R_x) &= R \cdot R_x \end{aligned} \]【計算の確認】
・右辺:分数の分母と分子の \( (R + R_x) \) が約分されて \( R \cdot R_x \) だけが残ります
・左辺:\( 0.8R \) に \( (R + R_x) \) が掛けられた状態です
よし、分数が消えたな!そしたら左辺の \( 0.8R(R + R_x) \) を展開してみよう。
分配法則を使うんや。\( a(b + c) = ab + ac \) っていうやつやな。中学校の数学を思い出してくれ〜
【ステップ6:左辺の展開】
現在の式:
→ 横スクロールして下さい →
\[ 0.8R(R + R_x) = R \cdot R_x \]左辺を分配法則で展開します:
→ 横スクロールして下さい →
\[ \begin{aligned} 0.8R \times R + 0.8R \times R_x &= R \cdot R_x \\[10pt] 0.8R^2 + 0.8R \cdot R_x &= R \cdot R_x \end{aligned} \]【展開の詳細】
・第1項:\( 0.8R \times R = 0.8R^2 \)
・第2項:\( 0.8R \times R_x = 0.8R \cdot R_x \)
これで左辺がすっきりと展開できました。
ナイス!展開できたな。そしたら次は、\( R_x \) の項を左辺に集めて、定数項を右辺に移してみよう。
方程式の基本は「同類項をまとめる」ことやからな。\( R_x \) が付いてる項と付いてない項を分けて考えるんや。
【ステップ7:項の移項と整理】
現在の式:
→ 横スクロールして下さい →
\[ 0.8R^2 + 0.8R \cdot R_x = R \cdot R_x \]\( R_x \) の項を左辺に集めるため、右辺の \( R \cdot R_x \) を左辺に移項します:
→ 横スクロールして下さい →
\[ \begin{aligned} 0.8R^2 + 0.8R \cdot R_x - R \cdot R_x &= 0 \\[10pt] 0.8R^2 + (0.8R - R) \cdot R_x &= 0 \\[10pt] 0.8R^2 + (-0.2R) \cdot R_x &= 0 \\[10pt] 0.8R^2 - 0.2R \cdot R_x &= 0 \end{aligned} \]【計算の確認】
\( 0.8R - R = 0.8R - 1.0R = -0.2R \) となります。
よっしゃ!もうちょっとやで。そしたら \( 0.8R^2 \) を右辺に移して、\( R_x \) について解いてみよう。
最後の仕上げや。計算ミスせんように慎重にいこな〜
【ステップ8:最終的な解の導出】
現在の式:
→ 横スクロールして下さい →
\[ 0.8R^2 - 0.2R \cdot R_x = 0 \]\( 0.8R^2 \) を右辺に移項します:
→ 横スクロールして下さい →
\[ \begin{aligned} -0.2R \cdot R_x &= -0.8R^2 \\[10pt] 0.2R \cdot R_x &= 0.8R^2 \\[10pt] R_x &= \frac{0.8R^2}{0.2R} \\[10pt] R_x &= \frac{0.8R^2}{0.2R} = \frac{0.8}{0.2} \times \frac{R^2}{R} \\[10pt] R_x &= 4 \times R = 4R \end{aligned} \]【計算の詳細】
・\( \frac{0.8}{0.2} = 4 \)
・\( \frac{R^2}{R} = R \)
したがって、\( R_x = 4R \, \mathrm{[\Omega]} \) です。
完璧や!\( R_x = 4R \) が求まったな。でも答えを出しただけじゃアカン。
この答えが本当に正しいか、元の式に代入して確認してみよう。これを「検算」っていうんや。試験でも絶対やっとくべきやで!
【ステップ9:解の検算】
求めた解:\( R_x = 4R \)
これを元の合成抵抗の式に代入して確認します:
→ 横スクロールして下さい →
\[ \begin{aligned} R_{ab} &= R + \frac{R \cdot R_x}{R + R_x} \\[10pt] &= R + \frac{R \times 4R}{R + 4R} \\[10pt] &= R + \frac{4R^2}{5R} \\[10pt] &= R + \frac{4R^2}{5R} \\[10pt] &= R + \frac{4R}{5} \\[10pt] &= \frac{5R}{5} + \frac{4R}{5} \\[10pt] &= \frac{9R}{5} = 1.8R \end{aligned} \]【検算結果】
計算結果が \( 1.8R \) となり、問題で与えられた条件と一致しました!
したがって、\( R_x = 4R \, \mathrm{[\Omega]} \) が正解です。
素晴らしい!検算もばっちりやな。そしたら選択肢を確認してみよう。
(1) \( R \) (2) \( 2R \) (3) \( 3R \) (4) \( 4R \) (5) \( 5R \)
答えは (4) \( 4R \) やな!一応、ほかの選択肢でも確認しよか
【ステップ10:選択肢の検討と最終確認】
正解:(4) \( 4R \)
【他の選択肢だとどうなるか】
例として (2) \( 2R \) の場合を確認してみましょう:
→ 横スクロールして下さい →
\[ \begin{aligned} R_{ab} &= R + \frac{R \times 2R}{R + 2R} \\[10pt] &= R + \frac{2R^2}{3R} \\[10pt] &= R + \frac{2R}{3} \\[10pt] &= \frac{3R + 2R}{3} = \frac{5R}{3} \approx 1.67R \end{aligned} \]これは \( 1.8R \) と一致しません。
【問題の特徴】
・この問題は合成抵抗の基本公式だけで解ける標準問題です
・計算過程で分数や小数が出てきますが、最終的には整数倍の答えになります
・検算を必ず行うことで、計算ミスを防げます
よっしゃ!完璧に解けたな。せやけど、もうちょっと深く考えてみよう。
この問題で使った「直並列回路の解法」は電験三種でよく出るパターンやから、解き方の手順をしっかり覚えとこな。どんな手順やったか振り返ってみよか?
【ステップ11:解法パターンの整理】
【直並列回路の標準解法手順】
1. 回路構造の把握:どの部分が直列で、どの部分が並列かを明確にする
2. 並列部分の処理:並列接続された抵抗の合成抵抗を先に求める
3. 直列部分の処理:並列合成抵抗と直列抵抗を足し合わせる
4. 方程式の設定:与えられた条件と合成抵抗の式を等式で結ぶ
5. 代数的解法:分数を消去し、移項を行い、未知数について解く
6. 検算による確認:求めた解を元の式に代入して条件を満たすか確認する
【この手順の重要性】
・電験三種の「理論」科目では、このパターンが頻出です
・一度覚えれば、抵抗値や回路構成が変わっても同じ手順で解けます
・計算ミスを防ぐために、各ステップを丁寧に行うことが重要です
ええ感じで整理できたな!そしたら最後に、この問題で学んだことを実際の電気回路でどう活かせるかも教えたるわ。
電験三種は資格試験やけど、実際の現場でも使える知識やからな。実務でこんな場面で役立つんやで!
まず配電系統の設計や。複数の負荷が並列接続された配電回路の抵抗計算、これは毎日のように使うで。ケーブルの直列抵抗と負荷の並列抵抗を考慮した電圧降下計算なんか、まさに今日やった内容そのものや。
それから接地抵抗の計算もそうや。複数の接地極が並列接続された場合の合成接地抵抗を求めたり、接地線の直列抵抗との組み合わせを考えたりするんは日常茶飯事やからな。
故障診断でも活躍するで。回路の一部に異常抵抗が発生した場合の影響度計算や、正常時と異常時の抵抗値比較による故障箇所の特定なんかで使うんや。
今回の \( R_x = 4R \) っていう結果も、現場的には「比較的大きな抵抗が並列に追加されたケースで、全体の抵抗は大きく下がらん」って判断材料になるんやで。数値感覚、大事やからな〜
なるほど!理論の勉強が実際の仕事に直結しているのですね。特に配電系統の設計で使われているというのは驚きです。
接地抵抗の並列接続による抵抗低下も、今日学んだ理論そのものですね。安全のために接地抵抗を小さくしたい時に、複数の接地極を使うという実用的な解決策になっているのが興味深いです。
故障診断では、正常値との比較で異常を発見するということですが、これはまさに「基準となる計算値」の重要性を示していますね。理論計算ができないと、故障かどうかの判断もできないということでしょうか。
数値感覚については、まだまだ身についていませんが、「4倍の抵抗が並列に追加されても大きな変化はない」ということを覚えておきます。現場ではこういう瞬間的な判断が求められるのですね。
そうそう、よう理解してくれたな!そしたら次に、この類の問題を解くときの「よくある間違い」と「対策」を教えたるわ。
試験本番で間違えんように、しっかり覚えときや〜。まず一番多いんが回路構造の読み違えや。全部を並列回路と勘違いしてしまう人が多いんやけど、回路図を端子から端子まで丁寧に辿って、電流の流れ方向を意識するのが大事やで。
それから公式の取り違えもよくあるな。並列合成抵抗の公式で分子と分母を逆にしてしまうんや。「分子は積、分母は和」って覚えとけば大丈夫や。「積和公式」って呼ぶ人も多いからな。
計算の途中でのミスも要注意や。\( 0.8R - R = 0.2R \) みたいな符号ミスは本当によくあるで。\( 0.8 - 1.0 = -0.2 \) を確実に計算するんや。小数の引き算は特に注意せなアカン。
そして一番もったいないんが検算の省略や。答えが出たらそのまま終了してしまう人が多いけど、必ず元の条件に代入して確認するんやで。時間がかかっても必須や!
覚え方のコツとしては、並列抵抗は「抵抗が小さくなる」ことを感覚的に覚えることと、\( 1.8R \) は \( R \) より大きいから直列部分があることを確認できるってことやな。
先生のお話で、自分の弱点がよく分かりました!確かに回路図を見るとき、つい全体を一度に理解しようとして混乱することがあります。一歩ずつ辿るという基本を大切にします。
「分子は積、分母は和」は覚えやすいですね!今まで毎回公式を思い出すのに時間がかかっていましたが、この覚え方なら迷わなくて済みそうです。
符号のミスは本当によくやってしまいます。\( 0.8 - 1.0 \) のような計算で、つい急いでしまって間違えるんです。もっと丁寧に、一つ一つ確認しながら計算することにします。
検算については、正直面倒に感じることもあったのですが、今日実際にやってみて「答えが合っている」という安心感が得られました。試験本番では特に重要ですね。
数値感覚はまだまだ不足していますが、「1.8は1より大きいから直列成分がある」という見方は、問題を解く前の予想に使えそうです!
よっしゃ!そういう意識を持ってくれれば安心や。最後に、この問題から派生して覚えておくべき「電験三種での頻出パターン」を教えたるで。
こういう応用問題が出ても慌てんように、しっかり頭に入れておこな〜
まず複数段の直並列回路や。今回は2段構成やったけど、3段、4段の組み合わせも出題されるからな。解法は同じで、外側から順番に合成抵抗を求めていくんや。
それから対称回路での等価変換もよく出る。ブリッジ回路や星形⇔三角形変換との組み合わせやけど、基本は今回と同じ合成抵抗の考え方やで。
条件付き問題も頻出やな。「電流が流れない条件は?」「電圧が等しくなる条件は?」みたいなやつや。これも合成抵抗の式を使って解けるんや。
そして今回みたいな数値の逆算問題も定番や。「結果から原因を求める」タイプやけど、方程式を立てて解く手順は共通やからな。
学習のポイントは、基本公式をしっかり覚えることが最重要や。計算練習を繰り返してミスを減らして、検算の習慣をつけて確実に得点する。そして回路図を正しく読み取る力を養う。この4つを意識してくれや!
わあ、電験三種ではこんなにバリエーションがあるのですね!今回の2段構成でも結構大変だったのに、3段、4段となると...でも「外側から順番に」という解法は同じということで、安心しました。
ブリッジ回路は名前だけは聞いたことがありますが、星形⇔三角形変換は初耳です。でも基本は合成抵抗ということなら、今日の学習が無駄にならないということですね。
「電流が流れない条件」や「電圧が等しくなる条件」という条件付き問題は、物理的な意味を理解していないと解けなさそうです。合成抵抗の計算だけでなく、回路の動作原理も勉強する必要がありますね。
逆算問題は今回初めて解きましたが、確かに方程式の立て方と解き方は同じパターンでした。慣れれば色々な問題に応用できそうです。
4つの学習ポイント、メモしました!特に「回路図を正しく読み取る力」は、全ての問題の出発点になりそうですね。図面を見る訓練も必要だと感じました。
完璧や!ここまでできれば、この手の問題はもう怖くないやろ?
最後に今日学んだことを簡単にまとめておこか。これで電験三種の抵抗回路問題は一歩前進やな!
今日のポイントを総復習すると、まず問題文の理解で \( R_{ab} = 1.8R \) から \( R_x = 4R \) を求める逆算問題やったな。回路構造の把握では、直列の \( R \) と並列の \( R \), \( R_x \) の組み合わせを正確に読み取った。段階的解法では、並列合成→全体合成→方程式→解法→検算の流れを確実にこなした。計算技術では、分数の処理、移項、因数分解を正確に行った。そして実務応用では、配電設計、接地抵抗、故障診断での活用方法を学んだな。
次のステップとしては、より複雑な直並列回路(3段、4段構成)、ブリッジ回路や対称回路の解法、インピーダンスを含む交流回路への発展、キルヒホフの法則を使った解法との比較なんかを勉強していけばええで。
継続学習のコツは、毎日少しずつでも計算練習を続ける、間違えた問題は必ず解き直す、公式の意味を理解して暗記する、実際の電気設備を見て回路をイメージするってことやな。
お疲れさまでした!この調子で頑張って、電験三種合格を目指そうな!
先生、今日はありがとうございました!
正直、最初は「また難しい計算問題か...」と思っていたのですが、先生の説明で一つ一つの手順がクリアになって、最後は「解ける!」という実感が持てました。
特に印象に残ったのは、「直並列回路は外側から順番に処理する」という考え方です。複雑に見える回路も、基本パターンの組み合わせなんですね。
検算で答えが一致したときは、本当に嬉しかったです。自分で計算した結果が正しいと確認できる瞬間は、達成感がありますね。
実務での応用例を聞いて、電験三種の勉強が「資格のためだけではない」ということも分かりました。将来現場で働くときのことを想像すると、やる気が出てきます。
明日からは、先生に教わった4つのポイントを意識して、毎日少しずつでも問題を解いてみます。次に出会う問題でも、今日の手順を思い出して落ち着いて取り組めそうです。
電験三種合格まで、頑張ります!
解説まとめ
問題回路図

■ 合成抵抗とは
合成抵抗とは、複数の抵抗が接続された回路において、それらを等価な一つの抵抗値として表現したものです。電気回路の解析において最も基本的かつ重要な概念の一つで、実務では配電設計や保護装置の選定において必須の知識となります。抵抗の接続方法(直列・並列)によって合成抵抗の計算方法が異なることを理解することが重要です。
直列合成抵抗

並列合成抵抗

■ 計算手順と公式
- 直列合成抵抗の計算
直列に接続された抵抗の合成抵抗は、各抵抗値の単純な和となります。
\( R = R_1 + R_2 + R_3 + \cdots \)
- 並列合成抵抗の計算
並列に接続された抵抗の合成抵抗は、各抵抗の逆数の和の逆数となります。
\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots \)
2つの抵抗が並列接続の場合は以下の公式が便利です:
\( R = \frac{R_1 R_2}{R_1 + R_2} \)
- 混合回路の解析手順
直列と並列が混在する回路では、電源から遠い部分から順次合成抵抗を計算していきます。
■ 具体的な計算例
問題条件
- 端子a,b間の合成抵抗:\( R_{ab} = 1.8R \ \mathrm{[\Omega]} \)
- 既知抵抗:\( R \ \mathrm{[\Omega]} \)
- 未知抵抗:\( R_x \ \mathrm{[\Omega]} \)
- 回路構成:抵抗\( R \)と抵抗\( R_x \)の並列接続が、別の抵抗\( R \)と直列接続
回路解析
回路図から、抵抗\( R \)と\( R_x \)が並列接続され、その合成抵抗が別の抵抗\( R \)と直列接続されています。
並列部分の合成抵抗:
\[ \begin{aligned} R_{parallel} &= \frac{R \cdot R_x}{R + R_x} \end{aligned} \]全体の合成抵抗:
\[ \begin{aligned} R_{ab} &= R + R_{parallel} \\[5pt] 1.8R &= R + \frac{R \cdot R_x}{R + R_x} \end{aligned} \]\( R_x \)の計算
上式を\( R_x \)について解きます:
→ 横スクロールして下さい
\[ \begin{aligned} 1.8R - R &= \frac{R \cdot R_x}{R + R_x} \\[5pt] 0.8R &= \frac{R \cdot R_x}{R + R_x} \\[5pt] 0.8R(R + R_x) &= R \cdot R_x \\[5pt] 0.8R^2 + 0.8R \cdot R_x &= R \cdot R_x \\[5pt] 0.8R^2 &= R \cdot R_x - 0.8R \cdot R_x \\[5pt] 0.8R^2 &= 0.2R \cdot R_x \\[5pt] R_x &= \frac{0.8R^2}{0.2R} = \frac{0.8R}{0.2} = 4R \ \mathrm{[\Omega]} \end{aligned} \]検算
\( R_x = 4R \)を代入して確認:
\[ \begin{aligned} R_{ab} &= R + \frac{R \cdot 4R}{R + 4R} \\[5pt] &= R + \frac{4R^2}{5R} \\[5pt] &= R + \frac{4R}{5} \\[5pt] &= \frac{5R + 4R}{5} = \frac{9R}{5} = 1.8R \ \mathrm{[\Omega]} \quad \checkmark \end{aligned} \]結論:抵抗\( R_x = 4R \ \mathrm{[\Omega]} \) 答え:(4)
■ 実務上の留意点
合成抵抗の計算は電気設備の設計・保守において極めて重要な基礎技術です。特に配電系統の短絡電流計算や保護装置の協調設定において必須の知識となります。
- 計算精度の重要性:保護装置の設定値に直接影響するため、計算ミスは設備事故につながる可能性があります
- 温度特性の考慮:実際の抵抗値は温度によって変化するため、設計時には温度係数を考慮する必要があります
- 配線抵抗の影響:長距離配線では配線自体の抵抗も合成抵抗に含めて計算する必要があります
- 並列回路の冗長性:並列接続は一つの経路が断線しても他の経路で電流が流れるため、信頼性向上に寄与します
- 電力損失の計算:合成抵抗値から回路全体の電力損失を計算し、エネルギー効率を評価できます