【理論】令和6年 (下期) 問6|直流電源を加えた抵抗の直並列回路における各抵抗の電流の計算問題
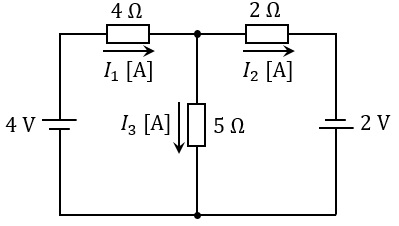
図のように,二つの直流電源と三つの抵抗からなる回路がある。
各抵抗に流れる電流を図に示す向きに定義するとき,電流 \( I_1 \),\( I_2 \),\( I_3 \) の値 \( [\mathrm{A}] \) の組合せとして,正しいものを次の (1)~(5) のうちから一つ選べ。
\[ \begin{array}{cccc} & I_1 & I_2 & I_3 \\ \hline (1) & -1 & -1 & 0 \\ \hline (2) & -1 & 1 & -2 \\ \hline (3) & 2 & 1 & 1 \\ \hline (4) & 1 & 1 & 0 \\ \hline (5) & 1 & -1 & 2 \\ \hline \end{array} \]
合格への方程式
重ね合わせの理
重ね合わせの理とは
重ね合わせの理(重ね合わせの定理)とは、複数の電源がある回路で、それぞれの電源を一つずつ動かして電流や電圧を計算し、最後にそれらを足し算して全体の値を求める方法です。例えば、複数のスピーカーから出る音が混ざって聞こえたり、いくつかの電球の明かりが重なって部屋全体を照らすのと同じ考え方です。
重ね合わせの理の適用条件
- 線形回路:抵抗、コイル、コンデンサなど線形素子のみ
- 独立電源:各電源が互いに独立している
- 時不変性:回路パラメータが時間変化しない
重ね合わせの理の手順
基本手順
- 電源の個別化:一つの電源のみを残し、他を無効化
- 個別回路の解析:各回路で電流・電圧を計算
- 結果の合成:各結果を代数的に加算
電源の無効化方法
電源を無効化する際の置き換え:
電源の置き換え規則
- 電圧源 → 短絡(電圧ゼロの導線)
- 電流源 → 開放(電流ゼロの空隙)
- 内部抵抗 → そのまま残す
具体的な解析例
本問題への適用
本問題の回路を重ね合わせの理で解いていきます。:

ステップ1:4V電源のみ作用させる
2V電源を短絡(導線)に置き換えます:
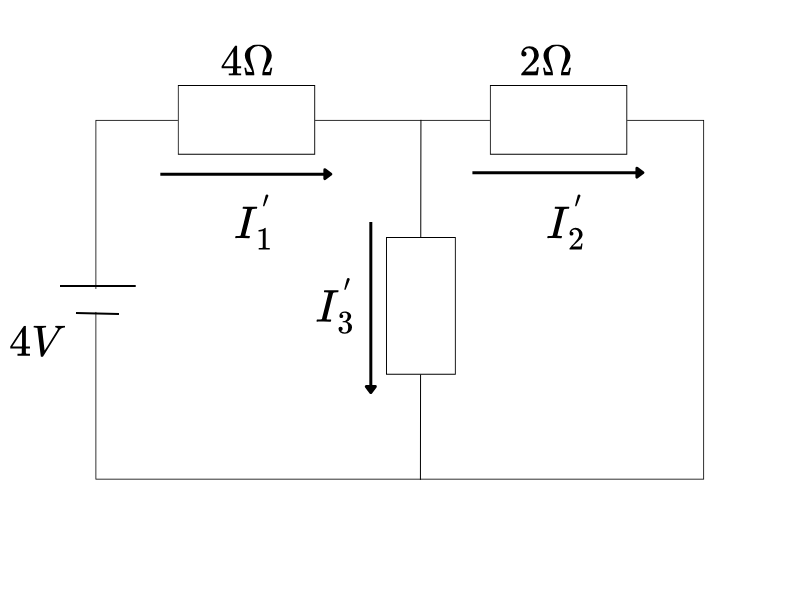
4V電源のみの場合の計算
合成抵抗の計算:
\[ R' = 4 + \frac{2 \times 5}{2 + 5} = 4 + \frac{10}{7} = \frac{38}{7} \, \Omega \]主回路電流:
\[ I_1' = \frac{4}{38/7} = \frac{28}{38} = \frac{14}{19} \, \mathrm{A} \]分流による各電流:
\[ I_2' = \frac{5}{2+5} \times I_1' = \frac{5}{7} \times \frac{14}{19} = \frac{10}{19} \, \mathrm{A} \] \[ I_3' = \frac{2}{2+5} \times I_1' = \frac{2}{7} \times \frac{14}{19} = \frac{4}{19} \, \mathrm{A} \]ステップ2:2V電源のみ作用させる
4V電源を短絡(導線)に置き換えます:
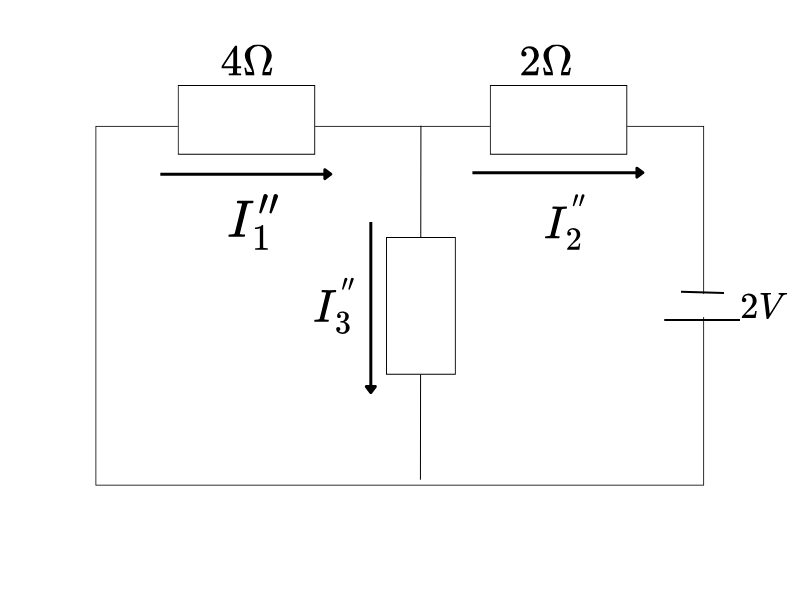
2V電源のみの場合の計算
合成抵抗の計算:
\[ R'' = 2 + \frac{4 \times 5}{4 + 5} = 2 + \frac{20}{9} = \frac{38}{9} \, \Omega \]主回路電流:
\[ I_2'' = \frac{2}{38/9} = \frac{18}{38} = \frac{9}{19} \, \mathrm{A} \]分流による各電流(方向に注意):
\[ I_1'' = \frac{5}{4+5} \times I_2'' = \frac{5}{9} \times \frac{9}{19} = \frac{5}{19} \, \mathrm{A} \] \[ I_3'' = -\frac{4}{4+5} \times I_2'' = -\frac{4}{9} \times \frac{9}{19} = -\frac{4}{19} \, \mathrm{A} \]ステップ3:結果の合成
各電源による結果を代数的に加算:
最終結果
\[ I_1 = I_1' + I_1'' = \frac{14}{19} + \frac{5}{19} = \frac{19}{19} = 1 \, \mathrm{A} \] \[ I_2 = I_2' + I_2'' = \frac{10}{19} + \frac{9}{19} = \frac{19}{19} = 1 \, \mathrm{A} \] \[ I_3 = I_3' + I_3'' = \frac{4}{19} + \left(-\frac{4}{19}\right) = 0 \, \mathrm{A} \]分圧・分流の法則
重ね合わせの理の計算では、分圧・分流の法則を頻繁に使用します。
分流の法則
並列回路において、電流は抵抗に反比例して分流されます:
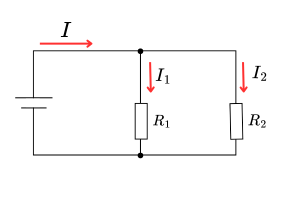
分流公式
総電流 I が抵抗 R₁ と R₂ に分流される場合:
\[ I_1 = \frac{R_2}{R_1 + R_2} \times I \] \[ I_2 = \frac{R_1}{R_1 + R_2} \times I \]重要:分子に来るのは相手の抵抗です(分圧とは逆)
分圧の法則
直列回路において、電圧は抵抗に比例して分圧されます:
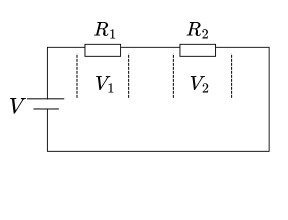
分圧公式
電圧 V が抵抗 R₁ と R₂ に分圧される場合:
\[ V_1 = \frac{R_1}{R_1 + R_2} \times V \] \[ V_2 = \frac{R_2}{R_1 + R_2} \times V \]合成抵抗の計算
直列合成
抵抗が直列に接続されている場合:
\[ R = R_1 + R_2 + R_3 + \cdots \]並列合成
抵抗が並列に接続されている場合:
\[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots \]2つの抵抗の場合:
\[ R = \frac{R_1 R_2}{R_1 + R_2} \]重ね合わせの理の利点と注意点
利点
- 計算の簡単化:複雑な回路を単純な回路に分解
- 直感的理解:各電源の寄与を個別に把握
- 設計への応用:各電源の影響を個別に評価
注意点
適用上の注意
- 線形素子のみ:ダイオードなど非線形素子には適用不可
- 電力計算:電力は重ね合わせできない(I²R、V²/R など)
- 符号の管理:電流・電圧の方向に注意
実用的な応用
回路設計での応用
重ね合わせの理は実際の回路設計で重要な役割を果たします:
実用応用例
- 電源回路:複数電源による電圧安定化の解析
- 信号処理:複数信号の合成・分離
- ノイズ解析:各ノイズ源の個別評価
- 感度解析:各パラメータ変化の影響評価
故障解析への応用
- 故障箇所の特定:各電源ごとの異常検出
- 負荷分散:各電源の負荷分担の評価
- 保護協調:複数保護装置の動作解析
重ね合わせの理は、複雑な電気回路を体系的に解析するための強力な手法です。各電源の個別の影響を理解することで、回路全体の動作を深く把握することができます。
ミルマンの定理
ミルマンの定理とは
ミルマンの定理とは、複数の電圧源と抵抗が並列につながった回路で、接続点の電圧を一度の計算で直接求められる定理です。重ね合わせの理よりも計算が楽になることが多く、特に並列回路を調べるときに便利な方法です。
ミルマンの定理の公式
n個の電圧源と抵抗の並列回路において、共通点の電位V は:
\[ V = \frac{\frac{E_1}{R_1} + \frac{E_2}{R_2} + \frac{E_3}{R_3} + \cdots + \frac{E_n}{R_n}}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots + \frac{1}{R_n}} \]ここで:
- \( E_i \):各電圧源の電圧 [V]
- \( R_i \):各枝の抵抗 [Ω]
- \( V \):共通接続点の電位 [V]
ミルマンの定理の物理的意味
コンダクタンスによる重み付け平均
ミルマンの定理は、各電圧源の電圧をコンダクタンス(1/R)で重み付けした平均として理解できます:
重み付け平均の考え方
- 分子:各電圧源が「どれだけ電流を送り出せるか」の合計
- 分母:全体の「電流の流れやすさ」の合計
- 結果:電流をたくさん流せる枝の電圧ほど、最終的な電圧への影響が大きい
電流源との類似性
各枝を電流源 \( I_i = E_i/R_i \)(電圧÷抵抗=電流)とコンダクタンス \( G_i = 1/R_i \)(電流の流れやすさ)の並列接続と考えることができます:
\[ V = \frac{I_1 + I_2 + \cdots + I_n}{G_1 + G_2 + \cdots + G_n} \]つまり、「全ての電流源から流れ出る電流の合計」を「全体の電流の流れやすさ」で割ることで、共通点の電圧が求まります。
ミルマンの定理の適用手順
基本手順
- 並列部分の特定:共通接続点を持つ枝を識別
- 各枝の値の設定:電圧源と抵抗の値を確認
- 符号の決定:電圧源の極性を統一
- 公式の適用:分子・分母を計算
- 電流の計算:必要に応じて各枝の電流を求める
符号の規則
電圧源の符号設定
- 正方向:共通点に向かう電圧源は正(+E)
- 負方向:共通点から離れる電圧源は負(-E)
- 電源なし:単純な抵抗の場合は E = 0
本問題への適用
回路の準備
本問題の回路をミルマンの定理で解析します:
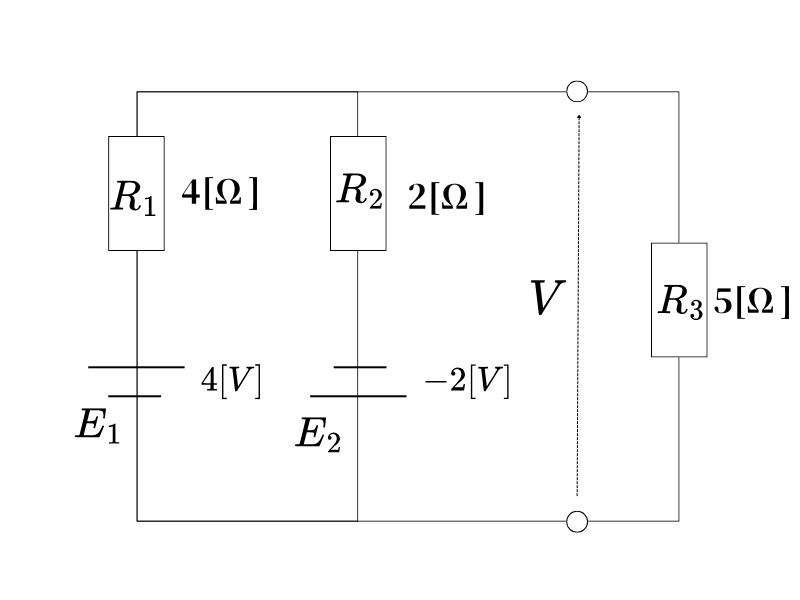
共通接続点の特定
5Ω抵抗の両端を共通接続点として考えます。この点の電位を求めることで、5Ω抵抗に流れる電流がわかります。
各枝の設定
- 枝1:E₁ = 4V、R₁ = 4Ω
- 枝2:E₂ = -2V、R₂ = 2Ω(極性に注意)
- 枝3:E₃ = 0V、R₃ = 5Ω(電源なし)
ミルマンの定理の適用
共通点電位の計算
\[ V = \frac{\frac{4}{4} + \frac{(-2)}{2} + \frac{0}{5}}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \] \[ V = \frac{1 - 1 + 0}{0.25 + 0.5 + 0.2} = \frac{0}{0.95} = 0 \, \mathrm{V} \]結果の解釈
5Ω抵抗の両端電位差がゼロということは:
I₃ = 0 の意味
- 電位差なし:5Ω抵抗の両端が同電位
- 電流ゼロ:I₃ = V/5 = 0/5 = 0 A
- 回路の簡化:5Ω抵抗は回路から除去可能
簡化された回路の解析
5Ω抵抗除去後の回路
I₃ = 0 がわかったので、5Ω抵抗を除去して考えることができます:
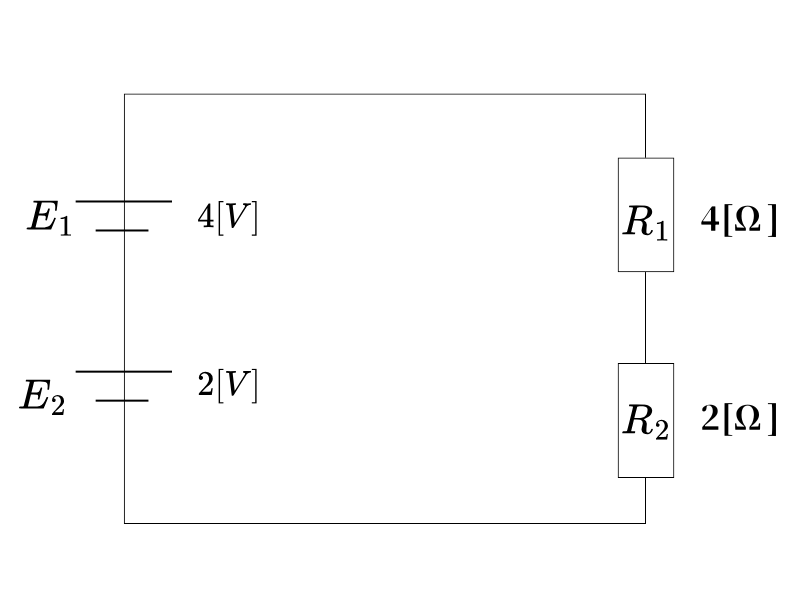
簡化回路での計算
4Ω抵抗と2Ω抵抗が直列接続され、全体に6Vが印加:
\[ I_1 = I_2 = \frac{4 + 2}{4 + 2} = \frac{6}{6} = 1 \, \mathrm{A} \]ミルマンの定理の応用技法
複雑な回路への適用
より複雑な回路でも、適切に分割することでミルマンの定理を適用できます:
適用のコツ
- 節点の選択:最も多くの枝が集まる点を選ぶ
- 基準点の設定:接地点(0V)を適切に設定
- 等価変換:複雑な枝を等価な電圧源と抵抗に変換
テブナンの定理との関係
ミルマンの定理は、テブナンの定理の特殊ケースとも考えられます:
\[ V_{th} = \frac{\frac{E_1}{R_1} + \frac{E_2}{R_2} + \cdots + \frac{E_n}{R_n}}{\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}}, \quad R_{th} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}} \]計算上の利点
重ね合わせの理との比較
計算量の比較
→ 横スクロールして下さい →
| 手法 | 計算回数 | 適用場面 | 利点 |
|---|---|---|---|
| 重ね合わせの理 | 電源数×回路解析 | 一般的な複数電源回路 | 理解しやすい、汎用性高い |
| ミルマンの定理 | 1回の計算 | 並列回路、節点電位 | 計算が速い、直接的 |
実用的な応用例
電力システムでの応用
実際の応用分野
- 配電システム:複数フィーダーの電圧計算
- 並列運転:複数発電機の負荷分担
- 電圧調整:複数調整器の協調動作
- 故障解析:短絡点の電位計算
回路設計での利用
- 基準電圧生成:分圧回路の設計
- バイアス回路:能動素子の動作点設定
- レベルシフト:信号電位の調整
注意事項と限界
適用上の注意
- 並列構造の確認:真に並列接続されている部分のみ適用
- 基準点の統一:全ての電圧の基準を統一
- 符号の管理:電圧源の極性を正確に把握
- 単位の統一:電圧・抵抗の単位を統一
発展的な理解
行列解法との関係
ミルマンの定理は、節点電位法(回路の各点の電圧を求める一般的な方法)の簡単な場合として考えることができます。節点電位法では次のような式を使います:
\[ [G][V] = [I] \]この式の意味は以下の通りです:
- [G]:各抵抗の「電流の流れやすさ」をまとめた表
- [V]:各点の電圧をまとめたリスト
- [I]:各点に流れ込む電流をまとめたリスト
ミルマンの定理は、この複雑な計算を並列回路に限って簡単にしたものです。つまり、面倒な連立方程式を解かなくても、一つの式で答えが出せる便利な方法なのです。
実践問題の解法
問題解法の基本戦略
複数電源を持つ直流回路の解析では、適切な解法手段の選択が重要です。回路の構造と求めるものに応じて、最も効率的な方法を選びましょう。
解法選択の指針
- ミルマンの定理:並列部分が多い、節点電位を求める
- 重ね合わせの理:全ての電流・電圧を求める、理解重視
- キルヒホッフの法則:複雑な回路、確実に解きたい
- 等価回路変換:対称性がある、回路を簡化できる
本問題の詳細解法
ステップ1:問題の理解と回路図の確認
与えられた条件を整理します:

- 電圧源:4V、2V
- 抵抗:4Ω、2Ω、5Ω
- 求めるもの:I₁、I₂、I₃の値
- 電流方向:図に示された向きで定義
ステップ2:解法の選択
本問題では2つの効果的な解法があります:
解法A:ミルマンの定理(推奨)
- 適用理由:5Ω抵抗の電位を直接求められる
- 計算量:少ない(1回の計算で解決)
- 理解:回路の本質的な特徴を把握
解法B:重ね合わせの理
- 適用理由:各電源の寄与を個別に理解
- 計算量:多い(2回の回路解析が必要)
- 理解:段階的で理解しやすい
解法A:ミルマンの定理による解法
ステップ1:5Ω抵抗の電位計算
5Ω抵抗の両端を共通接続点として、ミルマンの定理を適用:
並列枝の設定
- 枝1:4V電源 + 4Ω抵抗
- 枝2:2V電源 + 2Ω抵抗(逆向き)
- 枝3:5Ω抵抗(電源なし)
ミルマンの定理の適用:
\[ V_3 = \frac{\frac{4}{4} + \frac{(-2)}{2} + \frac{0}{5}}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \] \[ V_3 = \frac{1 - 1 + 0}{0.25 + 0.5 + 0.2} = \frac{0}{0.95} = 0 \, \mathrm{V} \]ステップ2:I₃の計算
5Ω抵抗の両端電位差がゼロなので:
\[ I_3 = \frac{V_3}{5} = \frac{0}{5} = 0 \, \mathrm{A} \]ステップ3:回路の簡化
I₃ = 0 なので、5Ω抵抗は回路から除去できます:

4Ω抵抗と2Ω抵抗が直列で、合計6Vが印加されています。
ステップ4:I₁、I₂の計算
簡化回路での計算
\[ I_1 = I_2 = \frac{4 + 2}{4 + 2} = \frac{6}{6} = 1 \, \mathrm{A} \]解法B:重ね合わせの理による解法
ステップ1:4V電源のみ作用させる
2V電源を短絡に置き換えます:

4V電源のみの場合
合成抵抗:
\[ R' = 4 + \frac{2 \times 5}{2 + 5} = 4 + \frac{10}{7} = \frac{38}{7} \, \Omega \]主電流:
\[ I_1' = \frac{4}{38/7} = \frac{28}{38} = \frac{14}{19} \, \mathrm{A} \]分流計算:
\[ I_2' = \frac{5}{2+5} \times \frac{14}{19} = \frac{5}{7} \times \frac{14}{19} = \frac{10}{19} \, \mathrm{A} \] \[ I_3' = \frac{2}{2+5} \times \frac{14}{19} = \frac{2}{7} \times \frac{14}{19} = \frac{4}{19} \, \mathrm{A} \]ステップ2:2V電源のみ作用させる
4V電源を短絡に置き換えます:

2V電源のみの場合
合成抵抗:
\[ R'' = 2 + \frac{4 \times 5}{4 + 5} = 2 + \frac{20}{9} = \frac{38}{9} \, \Omega \]主電流:
\[ I_2'' = \frac{2}{38/9} = \frac{18}{38} = \frac{9}{19} \, \mathrm{A} \]分流計算:
\[ I_1'' = \frac{5}{4+5} \times \frac{9}{19} = \frac{5}{9} \times \frac{9}{19} = \frac{5}{19} \, \mathrm{A} \] \[ I_3'' = -\frac{4}{4+5} \times \frac{9}{19} = -\frac{4}{9} \times \frac{9}{19} = -\frac{4}{19} \, \mathrm{A} \]ステップ3:重ね合わせ
最終結果の計算
\[ I_1 = I_1' + I_1'' = \frac{14}{19} + \frac{5}{19} = \frac{19}{19} = 1 \, \mathrm{A} \] \[ I_2 = I_2' + I_2'' = \frac{10}{19} + \frac{9}{19} = \frac{19}{19} = 1 \, \mathrm{A} \] \[ I_3 = I_3' + I_3'' = \frac{4}{19} + \left(-\frac{4}{19}\right) = 0 \, \mathrm{A} \]結果の検証
キルヒホッフの法則による確認
電流則(KCL)の確認
節点Aでの電流バランス:
\[ I_1 = I_2 + I_3 = 1 + 0 = 1 \, \mathrm{A} \quad \checkmark \]電圧則(KVL)の確認
左ループ:4V = 4Ω × 1A = 4V ✓
右ループ:2V = 2Ω × 1A = 2V ✓
選択肢との照合
計算結果:I₁ = 1A、I₂ = 1A、I₃ = 0A
- (1) -1, -1, 0 ← 符号が違う
- (2) -1, 1, -2 ← I₁の符号が違う
- (3) 2, 1, 1 ← I₁とI₃が違う
- (4) 1, 1, 0 ← 完全一致
- (5) 1, -1, 2 ← I₂とI₃が違う
答え:(4) I₁ = 1, I₂ = 1, I₃ = 0
計算のポイントと注意事項
1. 電流方向の定義
方向に関する注意
- 定義の確認:問題図の電流方向を正確に把握
- 符号の管理:計算中の符号を一貫して管理
- 結果の解釈:負の値は定義方向と逆向き
2. 計算精度の管理
分数計算を正確に行うか、十分な桁数で小数計算を行います:
計算方法の選択
- 分数計算:正確だが計算が複雑
- 小数計算:簡単だが丸め誤差に注意
- 検算:どちらの方法でも最終確認は必須
類似問題への対応
パターン1:電源数の変化
3個以上の電源がある場合:
- 重ね合わせの理:電源数だけ個別解析が必要
- ミルマンの定理:分子・分母に項を追加するだけ
パターン2:回路構造の変化
より複雑な回路の場合:
- 節点解析:多節点回路に適用
- 網目解析:多ループ回路に適用
- 等価変換:Δ-Y変換など
パターン3:非線形素子を含む場合
ダイオードなどが含まれる場合:
- 重ね合わせの理:適用不可
- 区分線形近似:各領域で線形化
- 数値解法:反復計算による解法
効率的な解法テクニック
1. 対称性の活用
本問題では4V/4Ωと2V/2Ωの比が同じ(1A相当)であることがポイント:
対称性による直感的理解
- 等価電流源:両方とも1Aの電流源として働く
- 方向の相殺:5Ω抵抗では電流が相殺
- 簡単な計算:複雑な計算が不要
2. 概算による検算
詳細計算前の概算確認:
- 電圧・抵抗比:4V/4Ω = 1A、2V/2Ω = 1A
- 対称性:同じ電流源効果 → I₃ = 0 の予想
- 直列回路:5Ω除去後は (4+2)V/(4+2)Ω = 1A
実用的な応用
電力システムでの類似問題
実際の応用例
- 配電フィーダー:複数変圧器からの電力供給
- 発電機並列運転:負荷分担の計算
- 系統連系:異なる電圧レベルの接続
- 故障解析:短絡時の電流分布
回路設計での応用
- 電源回路:複数電源による電圧安定化
- バッテリーシステム:並列接続による容量増加
- 負荷分散:複数電源による負荷分担
まとめ
この問題は、複数の解法が適用できる良い例題です。ミルマンの定理による解法は計算が簡潔で、回路の本質的な特徴(5Ω抵抗に電流が流れない)を直接的に示します。重ね合わせの理による解法は計算量は多いですが、各電源の寄与を明確に理解できます。
重要なポイント
- 解法選択:問題の構造に応じた最適な手法の選択
- 対称性の認識:4V/4Ω = 2V/2Ω = 1A という対称性
- 回路の簡化:I₃ = 0 による5Ω抵抗の除去
- 結果の検証:キルヒホッフの法則による確認
🔍 ワンポイントアドバイス: 複数電源回路では、まず回路の対称性や特徴を確認しましょう。本問では4V/4Ω = 2V/2Ω = 1Aという対称性から、5Ω抵抗に電流が流れないことが予想できます。ミルマンの定理で5Ω抵抗の電位がゼロであることを確認し、この抵抗を除去すれば簡単な直列回路になります。重ね合わせの理も有効ですが、計算量が多くなります。どちらの解法でも、最後はキルヒホッフの法則で検算を行い、選択肢と照合して正解を確定させましょう。
よっしゃ!今回は複数の電源がある回路の問題やな。まず最初に回路を見てもらおか。この回路、どんな特徴があるか分かるか?

はい、先生。この回路を見ると以下の特徴がありますね:
【回路の構成】
・2つの直流電源:4V と 2V
・3つの抵抗:4Ω、2Ω、5Ω
・電源と抵抗が組み合わさった複合回路
【回路の特徴】
・複数の電源があるため、単純なオームの法則だけでは解けない
・各抵抗に流れる電流の向きが定義されている
・5Ωの抵抗が中央に配置されて、他の回路と並列接続されている
【解法の選択肢】
このような回路は以下の方法で解析できます:
1. 重ね合わせの理(各電源の影響を個別に計算)
2. ミルマンの定理(並列回路の等価電圧を求める)
3. キルヒホッフの法則(連立方程式)
どの方法を使うかで計算の複雑さが変わりますね。
完璧な分析やな!複数電源の回路解析の理解もバッチリや。せやったら、まずは重ね合わせの理で解いてみよか。重ね合わせの理って、どんな原理やったか覚えてるか?
はい、重ね合わせの理(重ね合わせの定理)は:
【重ね合わせの理の原理】
複数の電源で構成された線形回路では、各電源が単独で動作したときの効果を個別に計算し、それらを代数的に加算することで全体の解を求めることができます。
【適用手順】
1. 電源を1つずつ残して、他の電源を除去
・電圧源 → 短絡(導線で置き換え)
・電流源 → 開放(切断)
2. 各電源単独での電流・電圧を計算
3. すべての結果を代数的に加算
・同じ向きなら加算
・逆向きなら減算
【なぜ使えるのか】
線形回路(抵抗、コイル、コンデンサ)では、オームの法則やキルヒホッフの法則がすべて線形関係なので、重ね合わせの原理が成り立ちます。
この問題では、4V電源と2V電源を1つずつ動作させて計算しますね。
その通りや!重ね合わせの理の理解も完璧やな。せやったら、まず4V電源だけを動作させた場合を考えてみよか。2V電源を短絡(除去)するとどんな回路になると思う?

はい、4V電源のみが動作している回路を見ると:
【回路の状態】
・4V電源:そのまま残す
・2V電源:短絡(導線に置き換え)
・結果:4V電源、4Ω抵抗、2Ωと5Ωの並列回路
【回路の解析】
1. 2Ωと5Ωの並列合成抵抗を求める
→ 横スクロールして下さい →
\[ \begin{aligned} R_{parallel} &= \frac{2 \times 5}{2 + 5} \\[10pt] &= \frac{10}{7} \\[10pt] &≈ 1.429 \, \mathrm{[\Omega]} \end{aligned} \]2. 全体の合成抵抗
→ 横スクロールして下さい →
\[ \begin{aligned} R' &= 4 + \frac{10}{7} \\[10pt] &= \frac{28 + 10}{7} \\[10pt] &= \frac{38}{7} ≈ 5.429 \, \mathrm{[\Omega]} \end{aligned} \]ええぞ!合成抵抗の計算も正確やな。せやったら、4V電源から流れる全電流 \(I_1'\) を求めて、それから分流の法則で \(I_2'\) と \(I_3'\) を計算してみよか。
はい、4V電源側の電流を計算します:
【全電流 \(I_1'\) の計算】
→ 横スクロールして下さい →
\[ \begin{aligned} I_1' &= \frac{4V}{R'} \\[10pt] &= \frac{4}{\frac{38}{7}} \\[10pt] &= \frac{4 \times 7}{38} \\[10pt] &= \frac{28}{38} \\[10pt] &≈ 0.7368 \, \mathrm{[A]} \end{aligned} \]【分流の法則で \(I_2'\) と \(I_3'\) を計算】
2Ωと5Ωの並列回路で、全電流 \(I_1'\) が分流します:
→ 横スクロールして下さい →
\[ \begin{aligned} I_2' &= \frac{5}{2+5} \times I_1' \\[10pt] &= \frac{5}{7} \times 0.7368 \\[10pt] &≈ 0.5263 \, \mathrm{[A]} \\[15pt] I_3' &= \frac{2}{2+5} \times I_1' \\[10pt] &= \frac{2}{7} \times 0.7368 \\[10pt] &≈ 0.2105 \, \mathrm{[A]} \end{aligned} \]【分流の法則のポイント】
並列回路では、抵抗値が小さい方により多くの電流が流れます。2Ω < 5Ωなので、\(I_2' > I_3'\) となっていますね。
完璧や!分流の法則の適用もバッチリやな。せやったら今度は、2V電源だけを動作させた場合を考えてみよか。4V電源を短絡するとどんな回路になるかな?

はい、2V電源のみが動作している回路を解析します:
【回路の状態】
・2V電源:そのまま残す
・4V電源:短絡(導線に置き換え)
・結果:2V電源、2Ω抵抗、4Ωと5Ωの並列回路
【4Ωと5Ωの並列合成抵抗】
→ 横スクロールして下さい →
\[ \begin{aligned} R_{parallel} &= \frac{4 \times 5}{4 + 5} \\[10pt] &= \frac{20}{9} \\[10pt] &≈ 2.222 \, \mathrm{[\Omega]} \end{aligned} \]【全体の合成抵抗】
→ 横スクロールして下さい →
\[ \begin{aligned} R'' &= 2 + \frac{20}{9} \\[10pt] &= \frac{18 + 20}{9} \\[10pt] &= \frac{38}{9} ≈ 4.222 \, \mathrm{[\Omega]} \end{aligned} \]興味深いことに、どちらの場合も分子が38になっていますね!これは偶然ではなく、回路の対称性を反映しています。
よう気づいたな!回路の対称性まで見抜くとは、さすがや。せやったら、2V電源から流れる全電流 \(I_2''\) を求めて、それから分流で \(I_1''\) と \(I_3''\) を計算してみよか。電流の向きに注意してな。
はい、2V電源側の電流を計算します:
【全電流 \(I_2''\) の計算】
→ 横スクロールして下さい →
\[ \begin{aligned} I_2'' &= \frac{2V}{R''} \\[10pt] &= \frac{2}{\frac{38}{9}} \\[10pt] &= \frac{2 \times 9}{38} \\[10pt] &= \frac{18}{38} \\[10pt] &≈ 0.4737 \, \mathrm{[A]} \end{aligned} \]【分流の法則で \(I_1''\) と \(I_3''\) を計算】
4Ωと5Ωの並列回路で、全電流 \(I_2''\) が分流します:
→ 横スクロールして下さい →
\[ \begin{aligned} I_1'' &= \frac{5}{4+5} \times I_2'' \\[10pt] &= \frac{5}{9} \times 0.4737 \\[10pt] &≈ 0.2632 \, \mathrm{[A]} \\[15pt] I_3'' &= -\frac{4}{4+5} \times I_2'' \\[10pt] &= -\frac{4}{9} \times 0.4737 \\[10pt] &≈ -0.2105 \, \mathrm{[A]} \end{aligned} \]【\(I_3''\) がマイナスの理由】
図を見ると、\(I_3''\) の向きが定義された \(I_3\) の向きと逆になっているため、マイナス符号がつきます。これは重ね合わせでは重要なポイントですね。
ええぞ!電流の向きまで正確に考慮できてるな。マイナス符号の理由も完璧や。せやったら、重ね合わせの最後のステップ、各電流成分を足し合わせて最終的な \(I_1\)、\(I_2\)、\(I_3\) を求めてみよか。
はい、重ね合わせの理により各電流を加算します:
【最終的な電流の計算】
→ 横スクロールして下さい →
\[ \begin{aligned} I_1 &= I_1' + I_1'' \\[10pt] &= 0.7368 + 0.2632 \\[10pt] &= 1.00 \, \mathrm{[A]} \\[15pt] I_2 &= I_2' + I_2'' \\[10pt] &= 0.5263 + 0.4737 \\[10pt] &= 1.00 \, \mathrm{[A]} \\[15pt] I_3 &= I_3' + I_3'' \\[10pt] &= 0.2105 + (-0.2105) \\[10pt] &= 0.00 \, \mathrm{[A]} \end{aligned} \]【結果の確認】
・\(I_1 = 1\,\mathrm{A}\)、\(I_2 = 1\,\mathrm{A}\)、\(I_3 = 0\,\mathrm{A}\)
選択肢と比較すると、(4) の組み合わせと一致しますね。
【興味深い結果】
\(I_3 = 0\) ということは、5Ωの抵抗には電流が流れていないということです。これは偶然ではなく、回路の電圧バランスによるものですね。
よっしゃ!重ね合わせの理による解法が完璧にできたな。\(I_3 = 0\) っていう結果、実は意味があるんや。せやったら今度は、ミルマンの定理でも解いてみよか。なんで \(I_3 = 0\) になるか、ミルマンの定理で確認してみ。

はい、ミルマンの定理を使って5Ωの抵抗の電圧を求めてみます:
【ミルマンの定理の適用】
図のように、3つの枝が並列接続されています:
・枝1:4V電源と4Ω抵抗
・枝2:2V電源と2Ω抵抗(逆向きなので-2V)
・枝3:5Ω抵抗のみ(電源なし、0V)
【5Ω抵抗にかかる電圧 \(V_3\) の計算】
→ 横スクロールして下さい →
\[ \begin{aligned} V_3 &= \frac{\frac{E_1}{R_1} + \frac{E_2}{R_2} + \frac{E_3}{R_3}}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} \\[15pt] &= \frac{\frac{4}{4} + \frac{-2}{2} + \frac{0}{5}}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[15pt] &= \frac{1 - 1 + 0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[15pt] &= \frac{0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} = 0 \, \mathrm{[V]} \end{aligned} \]【結果の解釈】
\(V_3 = 0\,\mathrm{V}\) なので、5Ω抵抗に電流は流れません:
\(I_3 = \frac{V_3}{5} = \frac{0}{5} = 0\,\mathrm{A}\)
これで重ね合わせの結果と一致しました!
完璧や!ミルマンの定理でも同じ結果が得られたな。\(I_3 = 0\) っていうのは、4V電源と2V電源の影響がちょうど打ち消し合ってるからなんや。せやったら、\(I_3 = 0\) を利用して、もっと簡単に \(I_1\) と \(I_2\) を求める方法があるで。どんな回路になると思う?

なるほど!\(I_3 = 0\) ということは、5Ωの抵抗を取り除いても回路の動作に影響しないということですね。
【簡略化された回路】
5Ωを除去すると、4V電源と4Ω抵抗、2V電源と2Ω抵抗が直列接続された単純な回路になります。
【電流の計算】
この回路では、4V + 2V = 6V の電圧が、4Ω + 2Ω = 6Ω の抵抗に加わります:
→ 横スクロールして下さい →
\[ \begin{aligned} I_1 = I_2 &= \frac{4 + 2}{4 + 2} \\[10pt] &= \frac{6}{6} \\[10pt] &= 1 \, \mathrm{[A]} \end{aligned} \]【この解法の利点】
1. 計算が圧倒的に簡単
2. 複雑な分流計算が不要
3. ミルマンの定理で先に \(I_3 = 0\) を確認できれば、この方法が使える
電験では、このような「回路の特性を見抜いて効率的に解く」技術が重要ですね。
素晴らしい解法やな!この「ミルマンで \(I_3 = 0\) を確認してから簡略化」っていうのは、電験でよく使われる技やから覚えとき。せやったら、なんで4V電源と2V電源の影響が5Ωでちょうど打ち消し合うんやろ?その理由を考えてみよか。
面白い質問ですね!これには回路の対称性と電圧比が関係しています:
【電圧と抵抗の比率】
・4V電源側:\(\frac{4V}{4Ω} = 1\,\mathrm{A/Ω}\)
・2V電源側:\(\frac{2V}{2Ω} = 1\,\mathrm{A/Ω}\)
この比率が同じなので、5Ωの両端の電位が等しくなります。
【物理的な説明】
5Ωの抵抗の両端を考えると:
・左端:4V電源から4Ωを通って到達する電位
・右端:2V電源から2Ωを通って到達する電位
4V電源が4Ωに対する影響と、2V電源が2Ωに対する影響が同じ「強さ」なので、中央点(5Ωの両端)の電位が等しくなります。
【一般的な条件】
この現象は \(\frac{E_1}{R_1} = \frac{E_2}{R_2}\) のとき発生します。
【実用的な意味】
・ブリッジ回路の平衡条件
・測定回路の零点調整
・電力系統の負荷分散
などでこの原理が活用されています。
よっしゃ!回路の本質まで理解できてるとは、本当に素晴らしいな。最後に、この問題を通して学んだことと、よくある間違いをまとめてもらえるか?電験でこの手の問題を確実に解くポイントも教えてな。
【この問題で学んだ重要ポイント】
1. 複数解法の習得
・重ね合わせの理:確実だが計算量多め
・ミルマンの定理:特定条件で効果的
・回路簡略化:最も効率的(条件が合えば)
2. 回路の物理的理解
・\(\frac{E_1}{R_1} = \frac{E_2}{R_2}\) で中央素子の電流が0
・対称性の認識で計算簡略化
【よくある間違いとその対策】
❌ 重ね合わせでの符号ミス
⭕ 電流の向きを図で必ず確認
❌ 分流の法則の公式間違い
⭕ 分子は「相手の抵抗」(分圧と逆)
❌ ミルマンで電源の極性無視
⭕ 逆向き電源は負の値で計算
❌ 並列合成抵抗の計算ミス
⭕ \(\frac{R_1 R_2}{R_1 + R_2}\) を確実に
【電験攻略のコツ】
1. まずミルマンで特殊条件をチェック
2. 対称性があれば簡略化を検討
3. 重ね合わせは最後の手段として確保
4. 計算結果は必ずキルヒホッフで検証
【実用的な応用】
・電力系統の潮流計算
・電子回路のバイアス設計
・測定機器の校正回路
・太陽光発電の並列運転
【時間短縮テクニック】
1. 選択肢から逆算:\(I_3 = 0\) の選択肢があれば、まずミルマンで確認
2. 対称性の活用:\(\frac{E_1}{R_1} = \frac{E_2}{R_2}\) なら即座に簡略化
3. 概算での検証:計算結果が物理的に妥当か確認
【答え:(4) \(I_1 = 1\), \(I_2 = 1\), \(I_3 = 0\)】
複数電源回路は電験の頻出分野なので、この3つの解法をマスターしておけば、どんな問題にも対応できますね!特に「効率的な解法の選択」ができるようになると、試験時間の大幅短縮につながります。
解説まとめ
■ 重ね合わせの理とミルマンの定理とは
複数の電源を含む直流回路の解析には、重ね合わせの理とミルマンの定理という2つの有効な手法があります。重ね合わせの理は、各電源が単独で作用する場合の電流を個別に計算し、それらを代数的に加算して最終的な電流を求める方法です。一方、ミルマンの定理は、並列に接続された複数の電源と抵抗を含む回路において、直接的に合成電圧を求めることができる定理です。両手法とも複雑な回路を効率的に解析するための重要な技法です。
■ 計算手順と公式
- 重ね合わせの理の適用
複数の電源がある回路では、各電源を個別に考えて電流を計算し、最後に合成します。
- 電圧源を短絡、電流源を開放して各電源の影響を個別に計算
- 各電源による電流を代数的に加算
- 合成抵抗の計算
直列接続と並列接続の合成抵抗を正確に計算します。
直列:\( R = R_1 + R_2 \)
並列:\( R = \frac{R_1 R_2}{R_1 + R_2} \)
- 分流の法則
並列回路での電流分配を計算します。
\( I_{R1} = \frac{R_2}{R_1 + R_2}I \)
\( I_{R2} = \frac{R_1}{R_1 + R_2}I \)
- ミルマンの定理
並列に接続された電源と抵抗の合成電圧を直接求めることができます。
\( V = \frac{\frac{E_1}{R_1} + \frac{E_2}{R_2} + \cdots}{\frac{1}{R_1} + \frac{1}{R_2} + \cdots} \)
■ 具体的な計算例
問題条件

- 電源1: 4V
- 電源2: 2V
- 抵抗1: 4Ω
- 抵抗2: 2Ω
- 抵抗3: 5Ω
解法1:重ね合わせの理による解析
4V電源のみが作用する場合

合成抵抗の計算:
\[ \begin{aligned} R' &= 4 + \frac{2 \times 5}{2 + 5} \\[5pt] &= 4 + \frac{10}{7} \\[5pt] &\approx 5.429 \ \Omega \end{aligned} \]4Ω抵抗を流れる電流:
\[ \begin{aligned} I_1' &= \frac{4}{R'} \\[5pt] &= \frac{4}{5.429} \\[5pt] &\approx 0.7368 \ \mathrm{[A]} \end{aligned} \]分流の法則により2Ω、5Ω抵抗の電流:
\[ \begin{aligned} I_2' &= \frac{5}{2+5} \times I_1' \\[5pt] &= \frac{5}{7} \times 0.7368 \\[5pt] &\approx 0.5263 \ \mathrm{[A]} \\[10pt] I_3' &= \frac{2}{2+5} \times I_1' \\[5pt] &= \frac{2}{7} \times 0.7368 \\[5pt] &\approx 0.2105 \ \mathrm{[A]} \end{aligned} \]2V電源のみが作用する場合

合成抵抗の計算:
\[ \begin{aligned} R'' &= 2 + \frac{4 \times 5}{4 + 5} \\[5pt] &= 2 + \frac{20}{9} \\[5pt] &\approx 4.222 \ \Omega \end{aligned} \]2Ω抵抗を流れる電流:
\[ \begin{aligned} I_2'' &= \frac{2}{R''} \\[5pt] &= \frac{2}{4.222} \\[5pt] &\approx 0.4737 \ \mathrm{[A]} \end{aligned} \]分流の法則により4Ω、5Ω抵抗の電流(電流方向に注意):
\[ \begin{aligned} I_1'' &= \frac{5}{4+5} \times I_2'' \\[5pt] &= \frac{5}{9} \times 0.4737 \\[5pt] &\approx 0.2632 \ \mathrm{[A]} \\[10pt] I_3'' &= -\frac{4}{4+5} \times I_2'' \\[5pt] &= -\frac{4}{9} \times 0.4737 \\[5pt] &\approx -0.2105 \ \mathrm{[A]} \end{aligned} \]重ね合わせによる最終結果
\[ \begin{aligned} I_1 &= I_1' + I_1'' \\[5pt] &= 0.7368 + 0.2632 \\[5pt] &= 1.00 \ \mathrm{[A]} \\[10pt] I_2 &= I_2' + I_2'' \\[5pt] &= 0.5263 + 0.4737 \\[5pt] &= 1.00 \ \mathrm{[A]} \\[10pt] I_3 &= I_3' + I_3'' \\[5pt] &= 0.2105 + (-0.2105) \\[5pt] &= 0.00 \ \mathrm{[A]} \end{aligned} \]解法2:ミルマンの定理による解析
ミルマンの定理を適用して5Ω抵抗の電圧を求めます:
 \[
\begin{aligned}
V_3 &= \frac{\frac{4}{4} - \frac{2}{2} + \frac{0}{5}}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= \frac{1 - 1 + 0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= \frac{0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= 0 \ \mathrm{[V]}
\end{aligned}
\]
\[
\begin{aligned}
V_3 &= \frac{\frac{4}{4} - \frac{2}{2} + \frac{0}{5}}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= \frac{1 - 1 + 0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= \frac{0}{\frac{1}{4} + \frac{1}{2} + \frac{1}{5}} \\[5pt]
&= 0 \ \mathrm{[V]}
\end{aligned}
\]
5Ω抵抗の電圧が0Vであるため、電流も0Aとなります:
\[ \begin{aligned} I_3 &= \frac{V_3}{5} = \frac{0}{5} = 0 \ \mathrm{[A]} \end{aligned} \]5Ω抵抗を取り除いた簡略回路:

残りの電流は簡単に計算できます:
\[ \begin{aligned} I_1 = I_2 &= \frac{4 + 2}{4 + 2} \\[5pt] &= \frac{6}{6} \\[5pt] &= 1 \ \mathrm{[A]} \end{aligned} \]結論:I₁ = 1 [A]、I₂ = 1 [A]、I₃ = 0 [A] である。(解答:選択肢(4))
■ 実務上の留意点
直流回路解析における重ね合わせの理とミルマンの定理の実務応用です。
- 重ね合わせの理は線形回路にのみ適用可能で、電力の計算には使用できません。電力は電流と電圧の積であり、非線形な関係があるためです。
- ミルマンの定理は、特に電源が多数ある並列回路で威力を発揮し、計算時間を大幅に短縮できます。
- 実際の回路では、内部抵抗や接触抵抗などの寄生要素も考慮する必要があり、理想的な計算値と実測値に差が生じることがあります。
- 電池を並列接続する際は、各電池の起電力や内部抵抗の違いにより循環電流が流れる可能性があるため、注意が必要です。
- 複雑な電力系統の解析では、これらの基本原理を応用したコンピュータシミュレーションが広く使用されています。
- 故障解析では、正常時と故障時の回路を重ね合わせの理で比較することにより、故障箇所の影響を定量的に評価できます。