【理論】令和6年 (下期) 問5|直流電源を加えた抵抗・コイル・コンデンサの直並列回路における蓄積エネルギーの計算問題
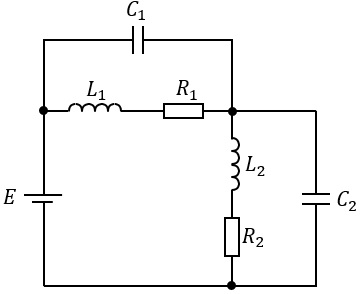
\( R_1 = 20 \ \Omega \),\( R_2 = 30 \ \Omega \) の抵抗,
インダクタンス \( L_1 = 20 \ \mathrm{mH} \),\( L_2 = 40 \ \mathrm{mH} \) のコイル,
および静電容量 \( C_1 = 400 \ \mu\mathrm{F} \),\( C_2 = 600 \ \mu\mathrm{F} \) のコンデンサからなる,図のような直並列回路がある。
直流電圧 \( E = 100 \ \mathrm{V} \) を加えたとき,定常状態において \( L_1 \),\( L_2 \),\( C_1 \) および \( C_2 \) に蓄えられるエネルギーの総和の値 \( [\mathrm{J}] \) として,
最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
過渡現象と定常状態
過渡現象とは何か?
過渡現象とは、回路の状態が変化してから新しい安定状態に達するまでの期間に起こる現象です。身近な例では、電灯のスイッチを入れた瞬間から安定して点灯するまでの僅かな時間や、モーターが始動してから定格回転数に達するまでの時間がこれに相当します。
過渡現象の特徴
- 時間的変化:電流や電圧が時間とともに変化
- 有限の継続時間:通常は数秒から数分で終了
- 初期条件依存:変化前の状態によって挙動が変わる
- 最終的安定:必ず定常状態に収束
コイル(インダクタンス)の過渡特性
コイルは電流の変化を妨げる性質があります。これはファラデーの電磁誘導の法則によるものです。
過渡状態(スイッチ投入直後)
コイルに電圧を印加した瞬間:
コイルの初期状態
- 電流:ほぼゼロ(急激な変化を妨げる)
- 電圧降下:印加電圧とほぼ等しい
- 等価回路:開放(無限大の抵抗)として扱う
- 物理的意味:磁場を作るためのエネルギー蓄積過程
定常状態(十分時間経過後)
コイルに電圧を印加して十分時間が経過した後:
コイルの定常状態
- 電流:オームの法則に従った一定値
- 電圧降下:巻線抵抗による降下のみ(理想的にはゼロ)
- 等価回路:短絡(抵抗ゼロ)として扱う
- 物理的意味:磁場エネルギーが最大で一定
コンデンサ(キャパシタンス)の過渡特性
コンデンサは電圧の変化を妨げる性質があります。これは電荷の蓄積・放出による現象です。
過渡状態(スイッチ投入直後)
コンデンサに電圧を印加した瞬間:
コンデンサの初期状態
- 電圧:ほぼゼロ(急激な変化を妨げる)
- 電流:最大値(充電電流)
- 等価回路:短絡(抵抗ゼロ)として扱う
- 物理的意味:電荷を蓄積するための充電過程
定常状態(十分時間経過後)
コンデンサに電圧を印加して十分時間が経過した後:
コンデンサの定常状態
- 電圧:印加電圧と等しい一定値
- 電流:ゼロ(これ以上充電されない)
- 等価回路:開放(無限大の抵抗)として扱う
- 物理的意味:電場エネルギーが最大で一定
コイルとコンデンサの対比
過渡特性の比較
| 素子 | 過渡状態(瞬間) | 定常状態(十分後) | 妨げる変化 |
|---|---|---|---|
| コイル(L) | 開放(電流≈0) | 短絡(電圧≈0) | 電流の変化 |
| コンデンサ(C) | 短絡(電圧≈0) | 開放(電流≈0) | 電圧の変化 |
| 抵抗(R) | 抵抗値R | 抵抗値R | 変化しない |
時定数の概念
過渡現象の継続時間は時定数によって決まります。
RC回路の時定数
抵抗RとコンデンサCからなる回路:
\[ \tau = RC \]ここで τ は時定数 [s] です。
RL回路の時定数
抵抗RとコイルLからなる回路:
\[ \tau = \frac{L}{R} \]時定数の意味
- 時間の目安:約5τ で定常状態の99%に到達
- 変化の速さ:時定数が小さいほど速く定常状態に到達
- 実用的判断:3τ で95%、5τ で99%が一般的な目安
直流回路における定常状態の重要性
直流回路の解析では、多くの場合定常状態を考えます。これは以下の理由によります:
- 実用性:機器の正常運転状態を表す
- 設計基準:定格値は定常状態での値
- 計算簡便:複雑な微分方程式が不要
- エネルギー評価:蓄積エネルギーは定常状態で最大
実際の回路での適用
本問題での適用
本問題では「定常状態において」という条件があるため:
等価回路の簡化
- L₁, L₂ → 短絡線(抵抗ゼロの導線)
- C₁, C₂ → 開放(電流の流れない空隙)
- R₁, R₂ → そのまま(抵抗値不変)
これにより複雑な回路が単純な抵抗回路に変換されます。
過渡現象の数学的表現
RC回路の過渡応答
コンデンサの充電過程:
\[ v_C(t) = V(1 - e^{-t/RC}) \]ここで V は印加電圧です。
RL回路の過渡応答
コイルの電流立ち上がり:
\[ i_L(t) = \frac{V}{R}(1 - e^{-Rt/L}) \]注意点
- 理想素子の仮定:実際には寄生成分がある
- 線形性の仮定:非線形素子では異なる挙動
- 温度依存性:温度により特性が変化
工学的意義
過渡現象の理解は以下の分野で重要です:
- 電源回路設計:起動時の過電流対策
- 保護装置:過渡的な異常値の判別
- 制御回路:応答速度の最適化
- EMC設計:スイッチングノイズの抑制
このような基礎理解により、実際の電気回路の動作を正確に予測・解析できるようになります。
エネルギー蓄積の基本
電気エネルギーとは
電気エネルギーは、電場や磁場に蓄えられるエネルギーのことです。身近な例では、携帯電話のバッテリーに蓄えられる化学エネルギーが電気エネルギーに変換されて利用されたり、雷雲に蓄積される静電エネルギーが放電時に大きな電流として現れます。
電気回路におけるエネルギー蓄積素子
- コイル(インダクタンス):磁場エネルギーを蓄積
- コンデンサ(キャパシタンス):電場エネルギーを蓄積
- 抵抗:エネルギーを蓄積せず、熱として消費
コイルの磁場エネルギー
コイルに電流が流れると、周囲に磁場が形成され、そこにエネルギーが蓄積されます。
基本公式
インダクタンス L [H] のコイルに電流 I [A] が流れるとき、蓄積される磁場エネルギー W [J] は:
\[ W = \frac{1}{2}LI^2 \]公式の導出
この公式は以下のように導出されます:
エネルギー導出の考え方
- コイルの基本式:\( v = L \frac{di}{dt} \)
- 瞬間電力:\( p = vi = Li \frac{di}{dt} \)
- エネルギー積分:\( W = \int_0^T p \, dt = \int_0^I Li \, di \)
- 積分実行:\( W = L \int_0^I i \, di = L \left[ \frac{i^2}{2} \right]_0^I = \frac{1}{2}LI^2 \)
物理的意味
磁場エネルギーの特徴:
磁場エネルギーの性質
- 可逆性:電流を切ると蓄積エネルギーが放出される
- 瞬時性:電流変化と同時にエネルギーも変化
- 空間分布:磁場が存在する空間全体に分布
- 非消費性:理想的なコイルではエネルギー損失なし
コンデンサの電場エネルギー
コンデンサに電圧が印加されると、電極間に電場が形成され、そこにエネルギーが蓄積されます。
基本公式
静電容量 C [F] のコンデンサに電圧 V [V] が印加されるとき、蓄積される電場エネルギー W [J] は:
\[ W = \frac{1}{2}CV^2 \]別の表現形式
電荷 Q = CV の関係を使うと、以下の形でも表現できます:
\[ W = \frac{1}{2}QV = \frac{Q^2}{2C} \]表現形式の使い分け
- \( W = \frac{1}{2}CV^2 \):電圧が既知の場合
- \( W = \frac{1}{2}QV \):電荷と電圧が既知の場合
- \( W = \frac{Q^2}{2C} \):電荷が既知の場合
公式の導出
コンデンサのエネルギー公式の導出:
充電過程でのエネルギー計算
- 充電電流:\( i = C \frac{dv}{dt} \)
- 瞬間電力:\( p = vi = Cv \frac{dv}{dt} \)
- エネルギー積分:\( W = \int_0^T p \, dt = \int_0^V Cv \, dv \)
- 積分実行:\( W = C \int_0^V v \, dv = C \left[ \frac{v^2}{2} \right]_0^V = \frac{1}{2}CV^2 \)
エネルギー密度の概念
電場・磁場エネルギーは空間に分布しており、単位体積あたりのエネルギー密度で表現できます。
電場エネルギー密度
電場の強さ E [V/m] の領域における電場エネルギー密度 u [J/m³] は:
\[ u = \frac{1}{2}\varepsilon E^2 \]ここで ε は誘電率 [F/m] です。
磁場エネルギー密度
磁束密度 B [T] の領域における磁場エネルギー密度 u [J/m³] は:
\[ u = \frac{1}{2\mu}B^2 \]ここで μ は透磁率 [H/m] です。
実際の計算例
コイルのエネルギー計算
計算例1:コイルのエネルギー
条件:L = 20 mH、I = 2 A
\[ \begin{aligned} W &= \frac{1}{2}LI^2 \\[10pt] &= \frac{1}{2} \times 20 \times 10^{-3} \times 2^2 \\[10pt] &= \frac{1}{2} \times 0.02 \times 4 \\[10pt] &= 0.04 \, \mathrm{J} \end{aligned} \]コンデンサのエネルギー計算
計算例2:コンデンサのエネルギー
条件:C = 400 μF、V = 40 V
\[ \begin{aligned} W &= \frac{1}{2}CV^2 \\[10pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 40^2 \\[10pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 1600 \\[10pt] &= 0.32 \, \mathrm{J} \end{aligned} \]エネルギーの保存と変換
電気回路におけるエネルギーは保存され、異なる形態間で変換されます。
エネルギー変換の例
- 充電過程:電源のエネルギー → コンデンサの電場エネルギー
- 放電過程:コンデンサの電場エネルギー → 回路の電気エネルギー
- 磁場蓄積:電源のエネルギー → コイルの磁場エネルギー
- 磁場放出:コイルの磁場エネルギー → 回路の電気エネルギー
単位の確認
エネルギー計算では単位の確認が重要です:
単位の整合性確認
コイルの場合:
\[ [W] = [L][I^2] = \mathrm{H} \cdot \mathrm{A^2} = \mathrm{J} \]コンデンサの場合:
\[ [W] = [C][V^2] = \mathrm{F} \cdot \mathrm{V^2} = \mathrm{J} \]実用的な応用
エネルギー貯蔵システム
エネルギー蓄積の原理は様々な技術に応用されています:
実用応用例
- スーパーキャパシタ:大容量コンデンサによる高速充放電
- SMES:超伝導コイルによる大容量磁場エネルギー貯蔵
- UPS:無停電電源装置での短時間エネルギー供給
- パルス電源:短時間での大電力供給
設計上の考慮事項
- エネルギー効率:蓄積・放出時の損失最小化
- 安全性:大エネルギー蓄積時の安全対策
- 寿命:繰り返し充放電に対する耐久性
- 温度特性:動作環境での特性変化
安全上の注意
大きなエネルギーを蓄積する素子では:
- 高電圧コンデンサ:感電や放電による危険
- 大電流コイル:開放時の誘導電圧による危険
- 適切な放電回路:安全な放電経路の確保
実践問題の解法
問題解法の基本戦略
直流回路におけるエネルギー蓄積問題は、定常状態での等価回路を正確に求めることが最も重要です。
解法の基本ステップ
- 定常状態の理解:コイル→短絡、コンデンサ→開放
- 等価回路の作成:簡化された回路図を描く
- 電流・電圧の計算:基本的な直流回路解析
- 各素子のエネルギー計算:適切な公式を適用
- 総エネルギーの算出:各エネルギーの合計
- 結果の確認:単位と桁数の妥当性チェック
本問題の詳細解法
ステップ1:与えられた条件の整理
回路定数を確認します:
- 抵抗:R₁ = 20Ω、R₂ = 30Ω
- インダクタンス:L₁ = 20mH、L₂ = 40mH
- 静電容量:C₁ = 400μF、C₂ = 600μF
- 直流電源:E = 100V
- 状態:定常状態
ステップ2:定常状態での等価回路
定常状態では:
素子の等価化
- L₁、L₂ → 短絡線(抵抗ゼロの導線)
- C₁、C₂ → 開放(電流が流れない)
- R₁、R₂ → そのまま(変化なし)
結果として、R₁とR₂が直列接続された単純な回路になります。
ステップ3:電流の計算
簡化された回路での電流計算:
直列回路の電流
全体の抵抗:\( R_{total} = R_1 + R_2 = 20 + 30 = 50\Omega \)
回路電流:
\[ I = \frac{E}{R_{total}} = \frac{100}{50} = 2 \, \mathrm{A} \]この電流がL₁とL₂の両方に流れます(直列接続のため)。
ステップ4:各コンデンサの電圧計算
コンデンサは開放状態なので、並列接続された抵抗の電圧降下と等しくなります:
コンデンサ電圧の計算
C₁の電圧(R₁と並列):
\[ V_1 = R_1 \times I = 20 \times 2 = 40 \, \mathrm{V} \]C₂の電圧(R₂と並列):
\[ V_2 = R_2 \times I = 30 \times 2 = 60 \, \mathrm{V} \]確認:V₁ + V₂ = 40 + 60 = 100V = E ✓
ステップ5:各素子の蓄積エネルギー計算
コイルのエネルギー計算
L₁のエネルギー:
\[ W_{L1} = \frac{1}{2}L_1 I^2 = \frac{1}{2} \times 20 \times 10^{-3} \times 2^2 = 0.04 \, \mathrm{J} \]L₂のエネルギー:
\[ W_{L2} = \frac{1}{2}L_2 I^2 = \frac{1}{2} \times 40 \times 10^{-3} \times 2^2 = 0.08 \, \mathrm{J} \]コンデンサのエネルギー計算
C₁のエネルギー:
\[ W_{C1} = \frac{1}{2}C_1 V_1^2 = \frac{1}{2} \times 400 \times 10^{-6} \times 40^2 = 0.32 \, \mathrm{J} \]C₂のエネルギー:
\[ W_{C2} = \frac{1}{2}C_2 V_2^2 = \frac{1}{2} \times 600 \times 10^{-6} \times 60^2 = 1.08 \, \mathrm{J} \]ステップ6:総エネルギーの計算
エネルギーの総和
\[ \begin{aligned} W_{total} &= W_{L1} + W_{L2} + W_{C1} + W_{C2} \\[10pt] &= 0.04 + 0.08 + 0.32 + 1.08 \\[10pt] &= 1.52 \, \mathrm{J} \end{aligned} \]ステップ7:選択肢との照合
計算結果1.52Jと選択肢を比較:
- (1) 0.12 ← 大幅に小さい
- (2) 1.20 ← やや小さい
- (3) 1.32 ← やや小さい
- (4) 1.40 ← 少し小さい
- (5) 1.52 ← 完全一致
答え:(5) 1.52
計算のポイントと注意事項
1. 単位変換の確認
重要な単位変換
- mH → H:20 mH = 20 × 10⁻³ H
- μF → F:400 μF = 400 × 10⁻⁶ F
- 最終単位:エネルギーは [J](ジュール)
2. 定常状態の正確な理解
よくある間違い
- コイルを開放として扱う → 正しくは短絡
- コンデンサを短絡として扱う → 正しくは開放
- 過渡状態と混同 → 問題文の「定常状態」を見落とす
3. 回路図の正確な読み取り
回路図から以下を正確に把握:
- 直列・並列関係:各素子の接続方法
- 電圧分担:どの素子間にどの電圧が印加されるか
- 電流経路:定常状態での電流の流れ
検算方法
1. 電圧の確認
キルヒホッフの電圧則による確認:
電圧バランス確認
E = V₁ + V₂ = 40 + 60 = 100V ✓
これは電源電圧と一致するので正しい。
2. エネルギー配分の確認
各素子のエネルギー比率を確認:
エネルギー配分
- コイル:0.04 + 0.08 = 0.12 J (約8%)
- コンデンサ:0.32 + 1.08 = 1.40 J (約92%)
- 合計:1.52 J
コンデンサの方がエネルギー蓄積量が大きいのは、電圧の2乗に比例するためです。
類似問題への対応
パターン1:異なる回路構成
並列接続が含まれる場合:
- 並列部分の合成:抵抗やリアクタンスの並列合成
- 電流分流:各枝の電流を個別に計算
- 電圧共通:並列部分では電圧が共通
パターン2:交流回路での応用
交流回路では:
- 実効値:交流電流・電圧の実効値を使用
- 位相関係:電流と電圧の位相差を考慮
- 平均エネルギー:時間平均のエネルギー
パターン3:過渡状態での問題
過渡現象を含む場合:
- 微分方程式:過渡応答の解析
- 初期条件:スイッチ投入前の状態
- 時間関数:エネルギーの時間変化
実用的な応用
電力システムでの応用
実際の応用例
- 電力コンデンサ:無効電力補償での蓄積エネルギー
- リアクトル:電流制限での磁場エネルギー
- UPS設計:必要エネルギー容量の算出
- 雷サージ対策:吸収エネルギーの評価
効率的な解法テクニック
1. 回路簡化の優先
複雑な計算前に回路を可能な限り簡化:
- 定常状態の適用:L→短絡、C→開放
- 直並列の整理:等価抵抗の計算
- 電圧・電流の一括計算:各素子の値を効率的に求める
2. 計算の系統化
計算ミスを防ぐための手順:
- 素子ごとの整理:L₁、L₂、C₁、C₂を個別に計算
- 中間結果の確認:各段階で妥当性をチェック
- 最終合計:全てのエネルギーを加算
3. 桁数の管理
適切な有効数字での計算:
- 中間計算:余分な桁数を保持
- 最終結果:問題で要求される精度に丸める
- 選択肢比較:有効数字を考慮した判定
エラーチェックのポイント
最終確認事項
- 単位の整合性:全ての計算で単位が[J]になっているか
- 物理的妥当性:エネルギーは正値か
- 桁数の妥当性:選択肢の範囲内か
- 計算の再現性:同じ結果が得られるか
まとめ
この問題は電気回路の基本的な解析能力を問う重要な問題です。定常状態での素子特性の理解、基本的な回路解析、エネルギー計算の各段階を確実にマスターすることで、より複雑な電力システムの問題にも対応できるようになります。
重要なポイントの再確認
- 定常状態:L→短絡、C→開放の原則
- エネルギー公式:\( W_L = \frac{1}{2}LI^2 \)、\( W_C = \frac{1}{2}CV^2 \)
- 回路解析:オームの法則とキルヒホッフの法則
- 計算精度:単位変換と有効数字の管理
🔍 ワンポイントアドバイス: 直流回路のエネルギー問題では、「定常状態」という条件が最重要です。この状態では、コイルは短絡(電流は流れるが電圧降下なし)、コンデンサは開放(電圧は加わるが電流は流れない)として扱います。回路が大幅に簡化されるので、まず等価回路を正確に描くことから始めましょう。その後、基本的なオームの法則で電流・電圧を求め、エネルギー公式 \( W_L = \frac{1}{2}LI^2 \)、\( W_C = \frac{1}{2}CV^2 \) で各素子のエネルギーを計算します。単位変換(mH→H、μF→F)に注意し、最後に全エネルギーを合計すれば答えが得られます。
よっしゃ!今回はRLC回路の直流定常状態でのエネルギー問題やな。まず最初に大事なことを聞くで。直流回路で「定常状態」って言われたら、コイルとコンデンサはどんな状態になるか分かるか?
はい、先生。直流回路の定常状態では:
【コイル(インダクタンス)】
・定常状態では電流が一定になるため、\(\frac{di}{dt} = 0\)
・コイルの電圧は \(v = L\frac{di}{dt} = 0\) になる
・つまり、コイルは短絡(ショート)として働く
【コンデンサ】
・定常状態では電圧が一定になるため、\(\frac{dv}{dt} = 0\)
・コンデンサの電流は \(i = C\frac{dv}{dt} = 0\) になる
・つまり、コンデンサは開放として働く
これは過渡現象の基本で、電源投入直後とは逆の状態になります。定常状態の回路解析では、コイルを導線に、コンデンサを切断した状態で考えます。
完璧や!過渡現象の理解もバッチリやな。「コイルは短絡、コンデンサは開放」これが定常状態の鉄則や。せやったら、この原理を使って与えられた回路を定常状態で簡略化してみよか。どんな回路になると思う?
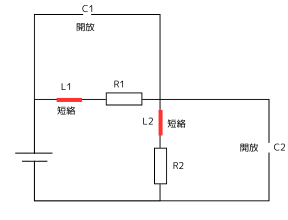
はい、定常状態での回路を考えてみます:
【回路の簡略化】
・\(L_1\) と \(L_2\):短絡(導線)として扱う
・\(C_1\) と \(C_2\):開放として扱う
すると、元の回路は以下のようになります:
・上の枝:\(R_1\) のみ(\(L_1\) は短絡、\(C_1\) は開放)
・下の枝:\(R_2\) のみ(\(L_2\) は短絡、\(C_2\) は開放)
【簡略化された回路】
電源 \(E = 100\,\mathrm{V}\) に対して、\(R_1 = 20\,\Omega\) と \(R_2 = 30\,\Omega\) が直列接続された単純な直流回路になります。
これで電流計算ができますし、各抵抗の電圧降下も求められます。コンデンサには各抵抗と同じ電圧が加わることになりますね。
その通りや!回路の見方が完璧やな。\(R_1\) と \(R_2\) が直列になった単純な回路になるわけや。せやったら、この回路に流れる電流を計算してみよか。オームの法則の出番やで!
はい、オームの法則を使って電流を計算します:
【回路の全抵抗】
\(R_1\) と \(R_2\) が直列接続されているので:
→ 横スクロールして下さい →
\[ \begin{aligned} R_{total} &= R_1 + R_2 \\[10pt] &= 20 + 30 \\[10pt] &= 50 \, \mathrm{[\Omega]} \end{aligned} \]【回路電流の計算】
オームの法則 \(I = \frac{V}{R}\) より:
→ 横スクロールして下さい →
\[ \begin{aligned} I &= \frac{E}{R_{total}} \\[10pt] &= \frac{100}{50} \\[10pt] &= 2 \, \mathrm{[A]} \end{aligned} \]つまり、\(L_1\) と \(L_2\) には同じ 2A の電流が流れることになります。
ええぞ!電流も正確に求められたな。2Aが \(L_1\) と \(L_2\) の両方に流れるんや。せやったら今度は、各抵抗にかかる電圧を求めてみよか。これがコンデンサの電圧にもなるからな。
はい、各抵抗の電圧降下を計算します:
【抵抗 \(R_1\) の電圧】
オームの法則 \(V = IR\) より:
→ 横スクロールして下さい →
\[ \begin{aligned} V_1 &= R_1 \times I \\[10pt] &= 20 \times 2 \\[10pt] &= 40 \, \mathrm{[V]} \end{aligned} \]【抵抗 \(R_2\) の電圧】
→ 横スクロールして下さい →
\[ \begin{aligned} V_2 &= R_2 \times I \\[10pt] &= 30 \times 2 \\[10pt] &= 60 \, \mathrm{[V]} \end{aligned} \]【検算】
\(V_1 + V_2 = 40 + 60 = 100\,\mathrm{V}\) で電源電圧と一致しているので正しいですね。
【コンデンサの電圧】
・\(C_1\) には \(V_1 = 40\,\mathrm{V}\) が印加
・\(C_2\) には \(V_2 = 60\,\mathrm{V}\) が印加
完璧や!電圧配分も正確やし、検算もバッチリやな。せやったら、エネルギー計算に入ろか。まずはコイルに蓄えられるエネルギーの公式、覚えてるか?
はい、コイル(インダクタンス)に蓄えられる磁気エネルギーの公式は:
→ 横スクロールして下さい →
\[ W_L = \frac{1}{2}LI^2 \]ここで、
・\(W_L\):磁気エネルギー \(\mathrm{[J]}\)
・\(L\):インダクタンス \(\mathrm{[H]}\)
・\(I\):電流 \(\mathrm{[A]}\)
【物理的意味】
コイルに電流が流れると磁界が発生し、その磁界にエネルギーが蓄えられます。電流が大きいほど、またインダクタンスが大きいほど、蓄えられるエネルギーも大きくなります。
この公式を使って \(L_1\) と \(L_2\) のエネルギーを計算できますね。両方とも同じ 2A の電流が流れているので計算しやすいです。
ええぞ!公式の理解もバッチリや。せやったら、\(L_1\) と \(L_2\) それぞれの磁気エネルギーを計算してみよか。単位に注意してな。インダクタンスはmH(ミリヘンリー)で与えられてるからな。
はい、各コイルの磁気エネルギーを計算します:
【\(L_1\) の磁気エネルギー】
与えられた値:\(L_1 = 20\,\mathrm{mH} = 20 \times 10^{-3}\,\mathrm{H}\)、\(I = 2\,\mathrm{A}\)
→ 横スクロールして下さい →
\[ \begin{aligned} W_{L1} &= \frac{1}{2}L_1 I^2 \\[10pt] &= \frac{1}{2} \times 20 \times 10^{-3} \times 2^2 \\[10pt] &= \frac{1}{2} \times 20 \times 10^{-3} \times 4 \\[10pt] &= \frac{1}{2} \times 80 \times 10^{-3} \\[10pt] &= 40 \times 10^{-3} \\[10pt] &= 0.04 \, \mathrm{[J]} \end{aligned} \]【\(L_2\) の磁気エネルギー】
与えられた値:\(L_2 = 40\,\mathrm{mH} = 40 \times 10^{-3}\,\mathrm{H}\)、\(I = 2\,\mathrm{A}\)
→ 横スクロールして下さい →
\[ \begin{aligned} W_{L2} &= \frac{1}{2}L_2 I^2 \\[10pt] &= \frac{1}{2} \times 40 \times 10^{-3} \times 4 \\[10pt] &= 0.08 \, \mathrm{[J]} \end{aligned} \]よっしゃ!コイルのエネルギー計算もバッチリやな。\(L_2\) は \(L_1\) の2倍のインダクタンスやから、エネルギーも2倍になってるのが分かるやろ?せやったら今度は、コンデンサのエネルギー公式はどうやったかな?
はい、コンデンサに蓄えられる静電エネルギーの公式は:
→ 横スクロールして下さい →
\[ W_C = \frac{1}{2}CV^2 \]ここで、
・\(W_C\):静電エネルギー \(\mathrm{[J]}\)
・\(C\):静電容量 \(\mathrm{[F]}\)
・\(V\):電圧 \(\mathrm{[V]}\)
【他の表現形式】
\(Q = CV\) の関係を使うと:
・\(\displaystyle W_C = \frac{1}{2}QV\)
・\(\displaystyle W_C = \frac{Q^2}{2C}\)
【物理的意味】
コンデンサに電荷が蓄えられると電界が発生し、その電界にエネルギーが蓄えられます。電圧の2乗に比例するので、電圧が高いほどエネルギーは急激に増加します。
今回は電圧で与えられているので、\(W_C = \frac{1}{2}CV^2\) を使いますね。
完璧や!コンデンサのエネルギーは電圧の2乗に比例するのがポイントやな。せやったら、\(C_1\) と \(C_2\) それぞれの静電エネルギーを計算してみよか。こっちも単位に注意や。μF(マイクロファラド)やからな。
はい、各コンデンサの静電エネルギーを計算します:
【\(C_1\) の静電エネルギー】
与えられた値:\(C_1 = 400\,\mathrm{\mu F} = 400 \times 10^{-6}\,\mathrm{F}\)、\(V_1 = 40\,\mathrm{V}\)
→ 横スクロールして下さい →
\[ \begin{aligned} W_{C1} &= \frac{1}{2}C_1 V_1^2 \\[10pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 40^2 \\[10pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 1600 \\[10pt] &= \frac{1}{2} \times 640 \times 10^{-3} \\[10pt] &= 320 \times 10^{-3} \\[10pt] &= 0.32 \, \mathrm{[J]} \end{aligned} \]【\(C_2\) の静電エネルギー】
与えられた値:\(C_2 = 600\,\mathrm{\mu F} = 600 \times 10^{-6}\,\mathrm{F}\)、\(V_2 = 60\,\mathrm{V}\)
→ 横スクロールして下さい →
\[ \begin{aligned} W_{C2} &= \frac{1}{2}C_2 V_2^2 \\[10pt] &= \frac{1}{2} \times 600 \times 10^{-6} \times 60^2 \\[10pt] &= \frac{1}{2} \times 600 \times 10^{-6} \times 3600 \\[10pt] &= 1.08 \, \mathrm{[J]} \end{aligned} \]ええぞ!コンデンサのエネルギー計算も正確やな。\(C_2\) のエネルギーが一番大きいのは、電圧が高い(60V)上に静電容量も大きい(600μF)からやな。せやったら、全部のエネルギーを合計してみよか。
はい、すべてのエネルギーを合計します:
【エネルギーの総和】
→ 横スクロールして下さい →
\[ \begin{aligned} W_{total} &= W_{L1} + W_{L2} + W_{C1} + W_{C2} \\[10pt] &= 0.04 + 0.08 + 0.32 + 1.08 \\[10pt] &= 1.52 \, \mathrm{[J]} \end{aligned} \]【各成分の内訳】
・コイル \(L_1\):0.04 J(2.6%)
・コイル \(L_2\):0.08 J(5.3%)
・コンデンサ \(C_1\):0.32 J(21.1%)
・コンデンサ \(C_2\):1.08 J(71.1%)
選択肢と比較すると、(5) \(1.52\) が正解ですね。
興味深いことに、\(C_2\) だけで全体の約7割のエネルギーを占めています。これは電圧の2乗効果(60V vs 40V)と大きな静電容量の相乗効果ですね。
完璧や!計算も正確やし、エネルギー配分の分析まで素晴らしいな。\(C_2\) が7割も占めてるのは、まさに電圧の2乗効果やな。ところで、なんで直流なのにコイルとコンデンサにエネルギーが蓄えられるんやろ?これって不思議やと思わへん?
確かに最初は不思議に感じますね!でも、これには明確な理由があります:
【なぜエネルギーが蓄えられるのか】
1. 電源投入の瞬間から定常状態まで
・電源を入れた瞬間:コイルは開放、コンデンサは短絡状態
・時間経過:徐々に電流と電圧が変化
・定常状態:コイルは短絡、コンデンサは開放状態
2. エネルギー蓄積の過程
・コイル:電流が0Aから2Aまで増加する過程で磁界エネルギーを蓄積
・コンデンサ:電圧が0Vから所定値まで充電される過程で静電エネルギーを蓄積
3. 定常状態での意味
定常状態では「変化がない」だけで、「エネルギーがない」わけではありません。むしろ、過渡現象の結果として確定した電流・電圧値に対応するエネルギーが蓄えられています。
つまり、直流だからこそ安定してエネルギーが蓄えられるんですね!
素晴らしい解説やな!過渡現象から定常状態への流れまで理解してるとは、さすがや。せやったら、実際の電気設備でこんなエネルギー蓄積がどう活用されてるか、知ってるか?
はい、実際の電気設備での活用例をご紹介します:
【コイルのエネルギー蓄積の活用】
・フライホイール効果:モーターの慣性と併せて回転の安定化
・チョークコイル:電流の急変を抑制して機器保護
・超電導磁気エネルギー貯蔵(SMES):大容量の瞬時電力供給
【コンデンサのエネルギー蓄積の活用】
・力率改善コンデンサ:誘導性負荷の無効電力補償
・平滑コンデンサ:整流回路の出力電圧安定化
・バックアップ電源:瞬停時の一時的な電力供給
・電気自動車:回生ブレーキのエネルギー回収
【この問題の実用的意味】
1.52Jというエネルギーは小さく見えますが、これは設計上重要な値です:
・機器の安全設計(放電時の危険性評価)
・エネルギー効率の計算
・保護回路の設計基準
特に高電圧機器では、蓄積エネルギーが人体に危険を与える可能性があるため、正確な計算が必要不可欠なんです。
よう勉強してるな!実用面まで考えられるとは感心するで。最後に、この問題でよくある間違いと、覚えておくべきポイントをまとめてもらえるか?
【よくある間違いとその対策】
1. 定常状態の理解不足
・❌ 交流のようにインピーダンスで計算してしまう
・⭕ 直流定常状態では「コイル短絡、コンデンサ開放」
2. 単位変換ミス
・❌ mH、μFをそのまま使用
・⭕ H、Fに変換してから計算(×10⁻³、×10⁻⁶)
3. エネルギー公式の混同
・❌ コイル:\(\frac{1}{2}LV^2\)、コンデンサ:\(\frac{1}{2}CI^2\)
・⭕ コイル:\(\frac{1}{2}LI^2\)、コンデンサ:\(\frac{1}{2}CV^2\)
4. 回路解析ミス
・❌ 各素子に異なる電流・電圧を考えてしまう
・⭕ 簡略化した回路で正確に電流・電圧を求める
【重要ポイントまとめ】
✅ 定常状態での素子の扱い:コイル短絡、コンデンサ開放
✅ エネルギー公式:コイル \(\frac{1}{2}LI^2\)、コンデンサ \(\frac{1}{2}CV^2\)
✅ 単位変換の確実な実行
✅ 過渡現象の物理的理解
答え:(5) 1.52
解説まとめ
■ RLC回路の定常状態とエネルギー蓄積とは
RLC回路において直流電圧を印加した場合、過渡状態を経て定常状態に至ります。定常状態では、コイル(インダクタ)は短絡として振る舞い、コンデンサは開放として振る舞います。この特性により、コイルには電流が流れて磁気エネルギーが蓄積され、コンデンサには電圧が加わって静電エネルギーが蓄積されます。各素子に蓄えられるエネルギーの総和を求めることで、回路全体のエネルギー収支を理解できます。
■ 計算手順と公式
- 定常状態における素子の振る舞い
直流定常状態では各素子の特性が変化します。
- コイル(インダクタ):短絡として振る舞う(抵抗 ≈ 0)
- コンデンサ:開放として振る舞う(抵抗 → ∞)
- 抵抗:そのままの抵抗値を維持
- コイルの磁気エネルギー
コイルに蓄えられる磁気エネルギーは次式で計算されます。
\( W_L = \frac{1}{2}LI^2 \)
ここで、WLは磁気エネルギー[J]、Lはインダクタンス[H]、Iは電流[A]です。
- コンデンサの静電エネルギー
コンデンサに蓄えられる静電エネルギーは次式で計算されます。
\( W_C = \frac{1}{2}CV^2 \)
ここで、WCは静電エネルギー[J]、Cは静電容量[F]、Vは電圧[V]です。
- 回路解析
定常状態における電流と電圧を計算し、各素子のエネルギーを求めます。
■ 具体的な計算例
問題条件
- 抵抗: \( R_1 = 20 \ \Omega \)、\( R_2 = 30 \ \Omega \)
- インダクタンス: \( L_1 = 20 \ \mathrm{mH} = 20 \times 10^{-3} \ \mathrm{H} \)
- インダクタンス: \( L_2 = 40 \ \mathrm{mH} = 40 \times 10^{-3} \ \mathrm{H} \)
- 静電容量: \( C_1 = 400 \ \mu\mathrm{F} = 400 \times 10^{-6} \ \mathrm{F} \)
- 静電容量: \( C_2 = 600 \ \mu\mathrm{F} = 600 \times 10^{-6} \ \mathrm{F} \)
- 直流電圧: \( E = 100 \ \mathrm{V} \)
定常状態における等価回路の解析
定常状態では、コイルは短絡、コンデンサは開放として振る舞うため、回路は抵抗 \( R_1 \) と \( R_2 \) の直列回路となります。
電流の計算
\( L_1 \) および \( L_2 \) に流れる電流は:
\[ \begin{aligned} I &= \frac{E}{R_1 + R_2} \\[5pt] &= \frac{100}{20 + 30} \\[5pt] &= \frac{100}{50} \\[5pt] &= 2 \ \mathrm{[A]} \end{aligned} \]各コンデンサの電圧計算
\( C_1 \) に加わる電圧(\( R_1 \) の両端電圧):
\[ \begin{aligned} V_1 &= R_1 I \\[5pt] &= 20 \times 2 \\[5pt] &= 40 \ \mathrm{[V]} \end{aligned} \]\( C_2 \) に加わる電圧(\( R_2 \) の両端電圧):
\[ \begin{aligned} V_2 &= R_2 I \\[5pt] &= 30 \times 2 \\[5pt] &= 60 \ \mathrm{[V]} \end{aligned} \]各素子の蓄積エネルギー計算
\( L_1 \) の磁気エネルギー:
\[ \begin{aligned} W_{L1} &= \frac{1}{2}L_1 I^2 \\[5pt] &= \frac{1}{2} \times 20 \times 10^{-3} \times 2^2 \\[5pt] &= \frac{1}{2} \times 20 \times 10^{-3} \times 4 \\[5pt] &= 0.04 \ \mathrm{[J]} \end{aligned} \]\( L_2 \) の磁気エネルギー:
\[ \begin{aligned} W_{L2} &= \frac{1}{2}L_2 I^2 \\[5pt] &= \frac{1}{2} \times 40 \times 10^{-3} \times 2^2 \\[5pt] &= \frac{1}{2} \times 40 \times 10^{-3} \times 4 \\[5pt] &= 0.08 \ \mathrm{[J]} \end{aligned} \]\( C_1 \) の静電エネルギー:
\[ \begin{aligned} W_{C1} &= \frac{1}{2}C_1 V_1^2 \\[5pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 40^2 \\[5pt] &= \frac{1}{2} \times 400 \times 10^{-6} \times 1600 \\[5pt] &= 0.32 \ \mathrm{[J]} \end{aligned} \]\( C_2 \) の静電エネルギー:
\[ \begin{aligned} W_{C2} &= \frac{1}{2}C_2 V_2^2 \\[5pt] &= \frac{1}{2} \times 600 \times 10^{-6} \times 60^2 \\[5pt] &= \frac{1}{2} \times 600 \times 10^{-6} \times 3600 \\[5pt] &= 1.08 \ \mathrm{[J]} \end{aligned} \]総エネルギーの計算
\[ \begin{aligned} W_{total} &= W_{L1} + W_{L2} + W_{C1} + W_{C2} \\[5pt] &= 0.04 + 0.08 + 0.32 + 1.08 \\[5pt] &= 1.52 \ \mathrm{[J]} \end{aligned} \]結論:L₁、L₂、C₁およびC₂に蓄えられるエネルギーの総和は 1.52 [J] である。(解答:選択肢(5))
■ 実務上の留意点
RLC回路のエネルギー蓄積に関する実務上の知見です。
- 電力系統では、コンデンサは無効電力の補償に使用され、その蓄積エネルギーは系統の安定性に影響します。適切な容量設計が重要です。
- 電子回路のスイッチング時には、コイルとコンデンサの蓄積エネルギーが急激に放出されることがあり、保護回路の設計に考慮が必要です。
- UPS(無停電電源装置)や電気自動車のエネルギー貯蔵では、コンデンサやインダクタの蓄積エネルギー特性を活用した設計が行われます。
- 高周波回路では、配線の寄生インダクタンスや寄生容量による予期しないエネルギー蓄積が回路性能に影響することがあります。
- 過渡現象の解析では、初期蓄積エネルギーが回路の応答特性を決定する重要な要素となります。
- エネルギー効率の観点から、不要なリアクティブエネルギーの蓄積を最小化する回路設計が求められます。