【理論】令和6年 (下期) 問16|ブリッジ回路による未知抵抗と電流に関する計算問題
図のブリッジ回路を用いて,未知抵抗 \( R_{x} \) を測定したい。
抵抗 \( R_{1} = 3 \) [kΩ],\( R_{2} = 2 \) [kΩ],\( R_{4} = 3 \) [kΩ] とし,\( R_{3} = 6 \) [kΩ] の滑り抵抗器の接触子の接点 \( \mathrm{C} \) をちょうど中央に調整したとき \( \left( R_{\mathrm{ac}} = R_{\mathrm{bc}} = 3 \ \mathrm{k\Omega} \right) \) ブリッジが平衡したという。
次の (a) 及び (b) の問に答えよ。
ただし,直流電圧源は \( 6 \) [V] とし,電流計の内部抵抗は無視できるものとする。
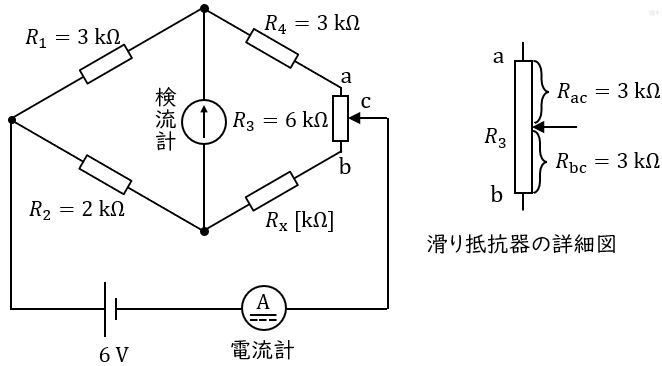
(a) 未知抵抗 \( R_{x} \) の値 [kΩ] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
(b) 平衡時の電流計の指示値 [mA] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
合格への方程式
ブリッジ回路の基本原理

ブリッジ回路とは何か?
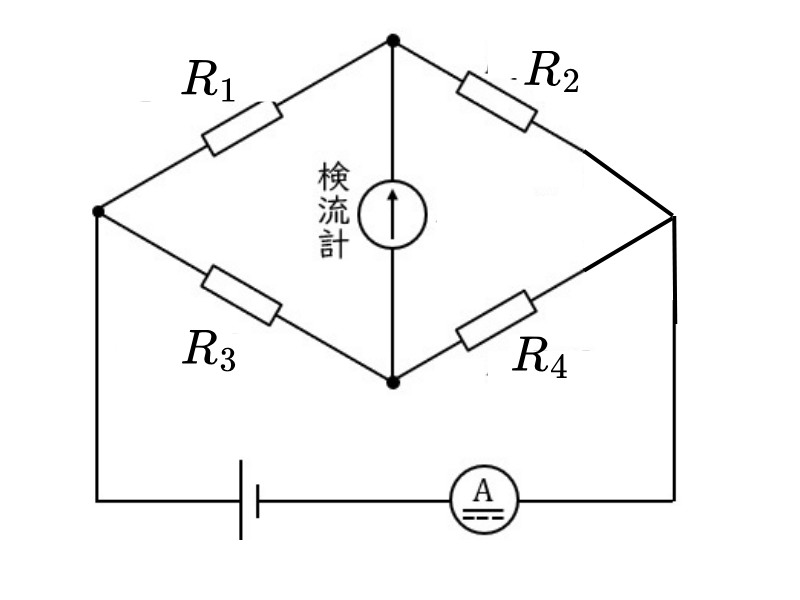
ブリッジ回路(ホイートストンブリッジ)は、未知の抵抗値を正確に測定するための回路です。この回路は、4つの抵抗がダイヤモンド型(菱形)に配置され、その中央に検流計(電流を測る器械)が接続されています。
なぜブリッジ回路が便利なのか?
普通の方法で抵抗を測ろうとすると、電圧計や電流計の内部抵抗が測定に影響してしまい、正確な値が得られないことがあります。しかし、ブリッジ回路なら検流計に電流が流れない「平衡状態」を利用するため、測定器の内部抵抗の影響を受けずに正確な測定ができます。
回路の構成要素
ブリッジ回路は以下の部品で構成されています:
- 4つの抵抗:\( R_1 \), \( R_2 \), \( R_3 \), \( R_4 \)(または \( R_x \))
- 直流電源:回路に電流を流すための電池
- 検流計:微小な電流を検出する精密な電流計
- 可変抵抗器:抵抗値を調整できる抵抗(滑り抵抗器)
検流計と電流計の違い
検流計は微小な電流(マイクロアンペア~ミリアンペア)を測定する精密な器械です。普通の電流計よりもずっと感度が高く、わずかな電流の変化も検出できます。ブリッジ回路では、この検流計の指示が「0」になる点を見つけることが重要です。
測定の基本的な考え方
ブリッジ回路の測定原理は、「電位差がゼロになる点を見つける」ことです。これは日常生活で例えると、シーソーのバランスを取るのと似ています。
シーソーの例え
シーソーで左右のバランスを取るとき、重い人は支点に近く、軽い人は支点から遠くに座りますよね。ブリッジ回路も同じで、抵抗の大きさと位置のバランスが取れたとき「平衡状態」になります。
ブリッジ回路の動作原理
電源から供給された電流は、回路の上下2つの経路に分かれて流れます:
- 上の経路:\( R_1 \) → \( R_4 \)
- 下の経路:\( R_2 \) → \( R_3 \)
検流計は、この2つの経路の中間点を結んでいます。もし上下の経路で電位の落ち方が同じなら、検流計の両端に電位差は生じず、電流は流れません。
よくある間違い
「検流計に電流が流れない」というのは、回路全体に電流が流れていないという意味ではありません。上下の経路にはそれぞれ電流が流れていますが、検流計の部分だけに電流が流れていない状態です。
ブリッジの平衡条件
平衡条件の式
ブリッジが平衡状態(検流計に電流が流れない状態)になるための条件は、以下の式で表されます:
 \[
R_1 \times R_4 = R_2 \times R_3
\]
\[
R_1 \times R_4 = R_2 \times R_3
\]
この式は「対角の抵抗の積が等しい」ことを表しています。
平衡条件の覚え方
ダイヤモンド型の回路で、「向かい合う抵抗をかけ算したものが等しい」と覚えましょう。つまり、斜め向かいの抵抗同士を掛け算します。
なぜこの式が成り立つのか?
平衡条件の式がなぜ成り立つのかを、電位の考え方で説明します。
検流計の両端をA点、B点とすると、平衡時には:
- A点の電位 = B点の電位
- つまり、A点とB点の電位差 = 0
これを数式で表すと:
\[ \begin{aligned} \frac{R_4}{R_1 + R_4} \times V &= \frac{R_3}{R_2 + R_3} \times V \\[10pt] \frac{R_4}{R_1 + R_4} &= \frac{R_3}{R_2 + R_3} \\[10pt] R_4(R_2 + R_3) &= R_3(R_1 + R_4) \\[10pt] R_4 R_2 + R_4 R_3 &= R_3 R_1 + R_3 R_4 \\[10pt] R_4 R_2 &= R_3 R_1 \\[10pt] R_1 R_4 &= R_2 R_3 \end{aligned} \]電位分割の考え方
上の計算では「電位分割」という考え方を使っています。抵抗が直列に接続されているとき、各抵抗にかかる電圧は、その抵抗値に比例して分割されます。これは、ケーキを人数に比例して分けるのと同じ考え方です。
平衡条件の実用的な使い方
実際の測定では、3つの抵抗値が分かっていて、1つの未知抵抗を求める場合がほとんどです。
未知抵抗の計算方法
\( R_x \) が未知抵抗の場合:
\[ R_x = \frac{R_2 \times R_3}{R_1} \]この式は平衡条件 \( R_1 R_x = R_2 R_3 \) を \( R_x \) について解いたものです。
滑り抵抗器を使った測定
実際のブリッジ回路では、滑り抵抗器(可変抵抗器)を使って平衡点を見つけます。
滑り抵抗器では、接触子の位置によって抵抗が2つの部分に分かれます:
- \( R_{ac} \):接触子より上の部分の抵抗
- \( R_{bc} \):接触子より下の部分の抵抗
- \( R_{ac} + R_{bc} = R_3 \)(全体の抵抗)
滑り抵抗器の平衡条件
滑り抵抗器を使った場合の平衡条件は:
\[ R_1(R_x + R_{bc}) = R_2(R_4 + R_{ac}) \]これは、各経路の合成抵抗を考慮した平衡条件です。
平衡点の見つけ方
実際の測定では、以下の手順で平衡点を見つけます:
- 滑り抵抗器の接触子を適当な位置に設定
- 検流計の指示を確認
- 電流が流れている場合は接触子を移動
- 検流計の指示が「0」になるまで調整を続ける
- 平衡点で接触子の位置を記録
測定時の注意点
検流計は非常に敏感な器械なので、平衡点近くでは接触子をゆっくりと動かして微調整することが大切です。急激に動かすと針が振り切れてしまうことがあります。
計算手順とテクニック
基本的な計算の流れ
ブリッジ回路の問題を解くときは、以下の順序で計算を進めます:
計算手順
- 平衡条件の確認:どの抵抗が未知かを把握
- 平衡条件式の適用:\( R_1 R_4 = R_2 R_3 \) を使用
- 未知抵抗の計算:式を変形して未知数を求める
- 合成抵抗の計算:平衡時の全体抵抗を求める
- 電流の計算:オームの法則で電流を求める
合成抵抗の計算方法
ブリッジが平衡している場合、検流計に電流が流れないので、検流計を取り除いて考えることができます。
平衡時の合成抵抗
平衡時は、上下の2つの経路が並列に接続された状態として計算します:
\[ R_{合成} = \frac{R_{上経路} \times R_{下経路}}{R_{上経路} + R_{下経路}} \]各経路の抵抗は:
- 上経路:\( R_1 + R_4 \)(直列接続)
- 下経路:\( R_2 + R_3 \)(直列接続)
滑り抵抗器がある場合の計算
滑り抵抗器を含む回路では、接触子の位置によって抵抗が分割されます。
滑り抵抗器を含む場合の各経路
- 上経路:\( R_1 + R_4 + R_{ac} \)
- 下経路:\( R_2 + R_x + R_{bc} \)
→ 横スクロールして下さい →
\[ \begin{aligned} R_{合成} &= \frac{(R_1 + R_4 + R_{ac})(R_2 + R_x + R_{bc})}{(R_1 + R_4 + R_{ac}) + (R_2 + R_x + R_{bc})} \\[10pt] &= \frac{上経路の抵抗 \times 下経路の抵抗}{上経路の抵抗 + 下経路の抵抗} \end{aligned} \]電流計算のポイント
全体の電流は、オームの法則を使って計算します:
\[ I = \frac{V}{R_{合成}} \]電流計と検流計の区別
問題文で「電流計の指示値」と聞かれた場合は、回路全体に流れる電流のことです。「検流計の指示値」と聞かれた場合は、平衡時には0になります。この区別を間違えやすいので注意しましょう。
単位の取り扱い
計算では単位に注意が必要です:
- 抵抗:\( \mathrm{k\Omega} \) と \( \mathrm{\Omega} \) の変換
- 電流:\( \mathrm{A} \) と \( \mathrm{mA} \) の変換
- 電圧:通常は \( \mathrm{V} \) で統一
単位変換のミス
\( 1 \mathrm{k\Omega} = 1000 \mathrm{\Omega} = 10^3 \mathrm{\Omega} \)
\( 1 \mathrm{A} = 1000 \mathrm{mA} = 10^3 \mathrm{mA} \)
計算の最後に単位を正しく変換することを忘れずに!
計算の検証方法
答えが正しいかどうかを確認する方法:
- 平衡条件の確認:求めた値で平衡条件式が成り立つか
- オーダーの確認:現実的な値になっているか
- 単位の確認:問題で求められている単位になっているか
検証の例
求めた \( R_x = 1 \mathrm{k\Omega} \) が正しいか確認:
\[ \begin{aligned} R_1 \times R_x &= 3 \times 1 = 3 \\[10pt] R_2 \times R_{ac} &= 2 \times 1.5 = 3 \end{aligned} \]両辺が等しいので、計算は正しいことが分かります。
よくある計算ミス
受験でよく見られる間違いとその対策:
| 間違いの種類 | 具体例 | 対策 |
|---|---|---|
| 平衡条件の適用ミス | 隣り合う抵抗を掛け算してしまう | 必ず「対角」の抵抗を確認 |
| 合成抵抗の計算ミス | 直列と並列の公式を間違える | 回路図を正確に読み取る |
| 単位変換ミス | k と m を混同する | 最後に単位を必ず確認 |
| 検流計と電流計の混同 | 平衡時の電流を間違える | 問題文をよく読む |
実践問題の解法
問題の概要
今回の問題では、以下の条件でブリッジ回路の測定を行います:
- \( R_1 = 3 \mathrm{k\Omega} \)、\( R_2 = 2 \mathrm{k\Omega} \)、\( R_4 = 3 \mathrm{k\Omega} \)
- \( R_3 = 6 \mathrm{k\Omega} \)の滑り抵抗器
- 接触子を中央に調整:\( R_{ac} = R_{bc} = 3 \mathrm{k\Omega} \)
- 直流電源:\( 6 \mathrm{V} \)
(a) 未知抵抗 \( R_x \) の計算
解法の手順
ステップ1:平衡条件式の設定
滑り抵抗器を含む場合の平衡条件:
\[ R_1(R_x + R_{bc}) = R_2(R_4 + R_{ac}) \]ステップ2:数値の代入
\[ \begin{aligned} 3(R_x + 3) &= 2(3 + 3) \\[10pt] 3(R_x + 3) &= 2 \times 6 \\[10pt] 3(R_x + 3) &= 12 \end{aligned} \]ステップ3:方程式を解く
\[ \begin{aligned} R_x + 3 &= \frac{12}{3} = 4 \\[10pt] R_x &= 4 - 3 = 1 \mathrm{k\Omega} \end{aligned} \]答え:(3) \( 1.0 \mathrm{k\Omega} \)
平衡条件を正確に適用することで、未知抵抗の値を求めることができました。
(b) 電流計の指示値の計算
解法の手順
ステップ1:回路の合成抵抗を求める
平衡時は検流計を無視して、2つの経路の並列接続として考えます:
- 上経路:\( R_1 + R_4 + R_{ac} = 3 + 3 + 3 = 9 \mathrm{k\Omega} \)
- 下経路:\( R_2 + R_x + R_{bc} = 2 + 1 + 3 = 6 \mathrm{k\Omega} \)
ステップ2:並列合成抵抗の計算
\[ \begin{aligned} R_{合成} &= \frac{R_{上} \times R_{下}}{R_{上} + R_{下}} \\[10pt] &= \frac{9 \times 6}{9 + 6} \\[10pt] &= \frac{54}{15} = 3.6 \mathrm{k\Omega} \end{aligned} \]ステップ3:電流の計算
\[ \begin{aligned} I &= \frac{V}{R_{合成}} \\[10pt] &= \frac{6}{3.6 \times 10^3} \\[10pt] &= \frac{6}{3600} \\[10pt] &= 1.67 \times 10^{-3} \mathrm{A} \\[10pt] &= 1.67 \mathrm{mA} \end{aligned} \]答え:(4) \( 1.7 \mathrm{mA} \)
合成抵抗の計算とオームの法則を組み合わせることで、回路全体に流れる電流を求めることができました。
解答の検証
平衡条件の検証
求めた \( R_x = 1 \mathrm{k\Omega} \) で平衡条件が成り立つか確認:
\[ \begin{aligned} \text{左辺:} R_1(R_x + R_{bc}) &= 3(1 + 3) = 12 \\[10pt] \text{右辺:} R_2(R_4 + R_{ac}) &= 2(3 + 3) = 12 \end{aligned} \]左辺 = 右辺なので、計算は正しいことが確認できます。
この問題のポイント
重要な注意点
- 電流計≠検流計:問題文の「電流計の指示値」は回路全体の電流のこと
- 滑り抵抗器の取り扱い:接触子の位置で抵抗が分割されることを理解
- 平衡条件の正確な適用:各経路の合成抵抗を考慮する
- 単位変換:最終的に求められている単位で答える
類似問題への応用
この解法は、以下のような類似問題にも応用できます:
- 異なる抵抗値を持つブリッジ回路
- 接触子の位置が異なる場合
- 電源電圧が異なる場合
- 複数の未知抵抗がある場合
応用問題の考え方
どのような変形問題でも、以下の基本手順は変わりません:
- 回路図を正確に読み取る
- 平衡条件式を正しく立てる
- 数値を代入して計算する
- 合成抵抗を求める
- 電流を計算する
- 答えを検証する
実際の測定での注意点
実際にブリッジ回路を使って測定する場合の注意点:
- 温度の影響:抵抗値は温度によって変化するため、測定環境に注意
- 接触抵抗:接触子と抵抗線の接触が悪いと誤差が生じる
- 電源の安定性:電源電圧が変動すると測定精度が落ちる
- 外部ノイズ:周囲の電磁気的ノイズが測定に影響することがある
🔍 ワンポイントアドバイス: ブリッジ回路の問題では「検流計の指示値」と「電流計の指示値」を区別することが最重要!平衡時は検流計=0、電流計=回路全体の電流です。また、平衡条件は「対角の抵抗の積が等しい」と覚え、滑り抵抗器では接触子で分割された各部分を含めて経路の合成抵抗を正確に計算しましょう。
今日はブリッジ回路の問題やな!これは電験三種でもよく出る重要な分野やで。まず回路図を見てもらおか。

このブリッジ回路で未知抵抗 \( R_x \) を測定するんや。ブリッジ回路って知ってるか?
はい、ブリッジ回路は抵抗値を精密に測定するための回路ですね。ホイートストンブリッジとも呼ばれています。4つの抵抗をダイヤモンド状に配置し、対角線上に電源と検流計を接続した構造になっています。
そうや!よく知ってるやん。このブリッジ回路の最大の特徴は「平衡条件」っちゅうのがあることなんや。平衡状態になったら検流計に電流が流れへん。この平衡条件、覚えてるか?
はい、ブリッジの平衡条件は次の式で表されます:
\[ R_1 \times R_4 = R_2 \times R_3 \]これは向かい合う抵抗の積が等しくなるという条件ですね。この状態では検流計に電流が流れません。
正解や!でもちょっと待ってや。回路図をよう見てみ。左上が \( R_1 = 3 \, \mathrm{k\Omega} \)、左下が \( R_2 = 2 \, \mathrm{k\Omega} \)、右上が \( R_4 = 3 \, \mathrm{k\Omega} \)、右下が \( R_x \) やな。そして \( R_3 \) の滑り抵抗器の接点Cが中央にあるから、この回路の平衡条件はどうなると思う?
回路図を確認すると、
・左上の辺が:\( R_1 = 3 \, \mathrm{k\Omega} \)
・左下の辺が:\( R_2 = 2 \, \mathrm{k\Omega} \)
・右上から接点のC辺が:\( R_4 + R_{ac} = 3 + 3 = 6 \, \mathrm{k\Omega} \)
・右下から接点Cの辺が:\( R_x + R_{bc} = R_x + 3 \, \mathrm{k\Omega} \)
したがって平衡条件は:\( R_1 \times (R_x + R_{bc}) = R_2 \times (R_4 + R_{ac}) \)
そうそう!よう考えてるな。ほんなら平衡条件を使って \( R_x \) を求めてみよか。数値を代入して計算してみて。
数値を代入して計算します:
\[ \begin{aligned} 3 \times (R_x + 3) &= 2 \times (3 + 3) \\[10pt] 3 \times (R_x + 3) &= 2 \times 6 \\[10pt] 3 \times (R_x + 3) &= 12 \end{aligned} \]ええ感じや!ほんなら両辺を3で割って \( R_x \) を求めてみよか。
両辺を3で割ります:
\[ \begin{aligned} R_x + 3 &= \frac{12}{3} \\[10pt] R_x + 3 &= 4 \\[10pt] R_x &= 4 - 3 \\[10pt] R_x &= 1 \, \mathrm{k\Omega} \end{aligned} \]したがって、未知抵抗 \( R_x = 1 \, \mathrm{k\Omega} \) となります。
正解や!(a)の答えは (3) の \( 1.0 \, \mathrm{k\Omega} \) やな。ところで、ブリッジが平衡してるときの検流計の電流は分かるやろ?
はい、ブリッジが平衡しているときは、検流計には電流が流れません。つまり検流計の電流は \( 0 \, \mathrm{mA} \) です。
これがブリッジ平衡の定義そのものですね。
そうや!でも問題文をもう一回よう読んでみ。(b)では「電流計の指示値」を聞いてるやろ?検流計やないで。電流計はどこにあると思う?
あっ、そうですね!問題をよく読み返すと、「電流計の指示値」となっています。
回路図を見ると、電流計は電源から回路全体に流れる電流を測定する位置にあります。つまり、回路全体の合成抵抗から全体の電流を求める必要があるということですね。
これは受験でよくある引っかけポイントですね。
その通りや!この間違い、受験生がよくやるパターンやから気ぃつけや。ブリッジが平衡してるときは、検流計の部分は切り離して考えてええねん。ほんなら回路全体の合成抵抗を求めてみよか。どんな風に計算したらええと思う?
ブリッジが平衡しているとき、検流計部分は電流が流れないので切り離して考えることができます。
すると回路は2つの並列回路になります:
・左側の経路:\( R_1 + R_2 = 3 + 2 = 5 \, \mathrm{k\Omega} \)
・右側の経路:\( (R_4 + R_{ac}) + (R_x + R_{bc}) = (3 + 3) + (1 + 3) = 6 + 4 = 10 \, \mathrm{k\Omega} \)
この2つが並列接続されているので、並列合成抵抗の公式を使います。
ちょっと待ってや!その考え方やと計算がおかしなるで。ブリッジが平衡してるとき、電流の流れ方をもうちょっと詳しく考えてみよか。検流計に電流が流れへんっちゅうことは、どういう経路で電流が流れるんやろ?
あっ、すみません!考え直してみます。
ブリッジが平衡しているとき、検流計には電流が流れないので、電流は次の2つの経路に分かれて流れます:
・経路1:電源 → \( R_1 \) → \( R_4 + R_{ac} \) → 電源
・経路2:電源 → \( R_2 \) → \( R_x + R_{bc} \) → 電源
つまり:
・経路1の抵抗:\( 3 + (3 + 3) = 9 \, \mathrm{k\Omega} \)
・経路2の抵抗:\( 2 + (1 + 3) = 6 \, \mathrm{k\Omega} \)
この2つが並列接続されています。
そうや!今度は正しいで。並列合成抵抗の公式、覚えてるか?2つの抵抗 \( R_a \) と \( R_b \) が並列に接続されてるとき、合成抵抗はどうなる?
並列合成抵抗の公式は次のとおりです:
\[ R = \frac{R_a \times R_b}{R_a + R_b} \]これを今回の場合に適用すると:
\[ R = \frac{9 \times 6}{9 + 6} = \frac{54}{15} \]ええ感じや!ほんなら \( \frac{54}{15} \) を計算してみよか。小数点で表すとどうなる?
\( \frac{54}{15} \) を計算します:
\[ \begin{aligned} R &= \frac{54}{15} \\[10pt] &= 3.6 \, \mathrm{k\Omega} \end{aligned} \]したがって、回路全体の合成抵抗は \( 3.6 \, \mathrm{k\Omega} \) です。
完璧や!ほんなら最後に電流計に流れる電流を求めてみよか。オームの法則使うねんで。電源電圧は6Vやったな。
オームの法則 \( I = \frac{V}{R} \) を使って電流を求めます:
\[ \begin{aligned} I &= \frac{V}{R} \\[10pt] &= \frac{6}{3.6 \times 10^3} \\[10pt] &= \frac{6}{3600} \\[10pt] &= 1.67 \times 10^{-3} \, \mathrm{A} \\[10pt] &= 1.67 \, \mathrm{mA} \end{aligned} \]ええ計算や!1.67mAやな。選択肢を見ると、一番近いのはどれやと思う?
計算結果は 1.67mA でした。選択肢を確認すると:
(1) 0 (2) 0.4 (3) 1.5 (4) 1.7 (5) 2.0
1.67 に最も近いのは (4) 1.7 ですね。
したがって、(b)の答えは (4) 1.7mA です。
正解や!よう頑張ったな。最後に今回のポイントをまとめてみよか。ブリッジ回路で一番重要なことは何やったと思う?
今回の重要ポイントをまとめます:
1. ブリッジの平衡条件
向かい合う抵抗の積が等しい:\( R_1 \times R_4 = R_2 \times R_3 \)
2. 滑り抵抗器の扱い
接点位置によって実効的な抵抗値が変わることを理解する
3. 検流計と電流計の違い
検流計:平衡時は0A、電流計:回路全体の電流を測定
4. 平衡時の回路解析
検流計部分を切り離して並列合成抵抗を計算
5. 計算の注意点
単位換算(kΩ → Ω、A → mA)を正確に行う
完璧やな!ブリッジ回路は測定技術でめちゃくちゃ重要やねん。実際の現場でも抵抗やインピーダンスの精密測定に使われてるで。この原理を応用したのがLCRメーターなんかの測定器や。電験三種でもよく出題されるから、今回の解法パターンはしっかり覚えといてな!
ありがとうございました!ブリッジ回路の理論と実際の応用がよく理解できました。
実用面での豆知識:
ホイートストンブリッジは1843年にサミュエル・ハンター・クリスティが発明し、チャールズ・ホイートストンが改良したことからこの名前がついています。現在でも高精度な抵抗測定の基本原理として、デジタル測定器の内部でも使われています。
覚え方のコツ:
平衡条件は「向かい合う抵抗の積が等しい」→「ダイヤモンドの対角線同士をかけて等しい」と覚えると忘れにくいです。
この問題形式は電験三種で頻出ですので、類似問題でも同じ解法が適用できます!
解説まとめ
問題回路図

■ ホイートストンブリッジ回路とは
ホイートストンブリッジ回路は、未知抵抗を高精度で測定するための代表的な測定回路です。4つの抵抗で構成されたブリッジ回路において、検流計の指示が零になる平衡条件を利用して未知抵抗値を求めます。この原理は電力系統の絶縁監視装置や各種センサーの校正において広く応用されており、電気主任技術者にとって重要な測定技術の基礎となります。
■ 計算手順と公式
ブリッジの平衡条件
検流計に電流が流れない(平衡)条件での抵抗の関係式です。
平衡条件:\( R_1 \times R_4 = R_2 \times R_3 \)
未知抵抗:\( R_x = \frac{R_2 \times R_3}{R_1} \)
合成抵抗の計算
平衡時は検流計を切り離して考えることができます。
直列:\( R = R_1 + R_2 + \cdots \)
並列:\( R = \frac{R_1 \times R_2}{R_1 + R_2} \)
オームの法則
電流計を流れる電流を求めるために使用します。
\( I = \frac{V}{R} \ \mathrm{[A]} \)
■ 具体的な計算例
問題条件
R₁=3kΩ、R₂=2kΩ、R₄=3kΩ、滑り抵抗器R₃=6kΩ(中央で分割:Rac=Rbc=3kΩ)、電源電圧6V、ブリッジ平衡状態
ブリッジ回路の構成

(a) 未知抵抗Rxの計算
Step 1: 平衡条件の適用
ブリッジ平衡時の条件式を立てます。接点Cで分割された回路では:
\[ \begin{aligned} R_1 \times (R_x + R_{bc}) &= R_2 \times (R_4 + R_{ac}) \end{aligned} \]Step 2: 数値の代入
\[ \begin{aligned} 3 \times (R_x + 3) &= 2 \times (3 + 3) \\[5pt] 3 \times (R_x + 3) &= 2 \times 6 \\[5pt] 3 \times (R_x + 3) &= 12 \end{aligned} \]Step 3: 未知抵抗の計算
\[ \begin{aligned} R_x + 3 &= \frac{12}{3} \\[5pt] R_x + 3 &= 4 \\[5pt] R_x &= 4 - 3 \\[5pt] R_x &= 1 \ \mathrm{k\Omega} \end{aligned} \](b) 平衡時の電流計指示値の計算
Step 1: 等価回路の考え方
ブリッジが平衡しているとき、検流計には電流が流れないので、検流計を切り離して考えることができます。この場合、2つの直列回路が並列接続されている状態となります。
Step 2: 各枝の抵抗計算
上側の枝:
\[ \begin{aligned} R_{上} &= R_1 + R_4 + R_{ac} \\[5pt] &= 3 + 3 + 3 \\[5pt] &= 9 \ \mathrm{k\Omega} \end{aligned} \]下側の枝:
\[ \begin{aligned} R_{下} &= R_2 + R_x + R_{bc} \\[5pt] &= 2 + 1 + 3 \\[5pt] &= 6 \ \mathrm{k\Omega} \end{aligned} \]Step 3: 並列合成抵抗の計算
\[ \begin{aligned} R_{合成} &= \frac{R_{上} \times R_{下}}{R_{上} + R_{下}} \\[5pt] &= \frac{9 \times 6}{9 + 6} \\[5pt] &= \frac{54}{15} \\[5pt] &= 3.6 \ \mathrm{k\Omega} \end{aligned} \]Step 4: 電流計の電流計算
\[ \begin{aligned} I &= \frac{V}{R_{合成}} \\[5pt] &= \frac{6}{3.6 \times 10^3} \\[5pt] &= \frac{6}{3600} \\[5pt] &= 1.67 \times 10^{-3} \ \mathrm{A} \\[5pt] &= 1.67 \ \mathrm{mA} \end{aligned} \]重要なポイント
問題(b)で求めるのは「電流計」の指示値です。「検流計」の指示値ではありません。ブリッジが平衡している状態では検流計の指示は0mAですが、電源から回路全体に流れる電流(電流計の指示)は0ではありません。
計算結果まとめ
| 項目 | 記号 | 値 | 単位 |
|---|---|---|---|
| 未知抵抗 | \( R_x \) | 1.0 | kΩ |
| 上側枝抵抗 | \( R_{上} \) | 9.0 | kΩ |
| 下側枝抵抗 | \( R_{下} \) | 6.0 | kΩ |
| 合成抵抗 | \( R_{合成} \) | 3.6 | kΩ |
| 電流計指示値 | \( I \) | 1.67 | mA |
結論:
(a) 未知抵抗 Rx = 1.0 kΩ 答え:(3)
(b) 電流計指示値 I = 1.67 mA ≈ 1.7 mA 答え:(4)
■ 実務上の留意点
ホイートストンブリッジ回路は、精密測定や校正において重要な役割を果たします。特に絶縁監視や温度測定において広く活用されている技術です。
測定精度の向上:高精度測定のためには温度変化による抵抗値変動を考慮し、温度補償回路や恒温槽での測定を検討する必要があります。絶縁監視への応用:接地系統の絶縁監視装置では、ブリッジ回路の原理を応用して地絡抵抗を監視し、絶縁劣化の早期発見を図っています。センサー校正:測温抵抗体(RTD)や歪みゲージなどの抵抗式センサーの校正において、標準抵抗器との比較測定に使用されます。
ノイズ対策:高精度測定では電磁ノイズの影響を避けるため、シールド線の使用や測定環境の改善が重要です。また、交流励起を用いた交流ブリッジも検討されます。自動平衡装置:連続監視システムでは、機械的な平衡操作に代わり、電子回路による自動平衡機能を持つデジタルブリッジが使用されます。安全対策:高電圧回路での絶縁測定では、測定者の安全確保と測定回路の絶縁設計が重要です。適切な保護具の使用と安全手順の遵守が必要です。校正管理:測定精度を維持するため、標準抵抗器の定期校正と測定器の校正証明書管理を適切に行う必要があります。