【理論】令和6年(上期)　問5｜直流電源を加えた直並列回路における特定抵抗の消費電力に関する計算問題

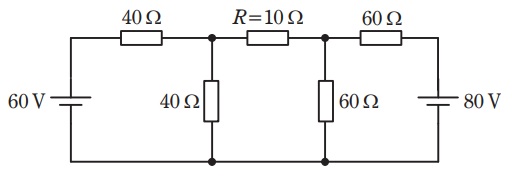
図の直流回路において，抵抗 \( R = 10 \ \mathrm{\Omega} \) で消費される電力の値 [W] として，最も近いものを次の (1)～(5) のうちから一つ選べ。

回路図

合格への方程式

重ね合わせの理（重ね合わせの定理）の基礎

重ね合わせの理とは？

複数の電源を持つ回路において、各電源が単独で作る電流（または電圧）を別々に計算し、それらを足し合わせて全体の電流（または電圧）を求める方法です。線形回路でのみ使える超便利な解法です！

■ 重ね合わせの理の手順

ステップ 作業内容 注意点
Step 1 1つの電源だけを残す 他の電源は除去する
Step 2 電源の除去方法
・電圧源→短絡
・電流源→開放		 抵抗はそのまま残す
Step 3 各電源での電流を計算 方向に注意
Step 4 全電流を重ね合わせ 向きを考慮して加減算

■ なぜ電圧源は短絡、電流源は開放？

理想電源の特性から理解する

• 理想電圧源：内部抵抗ゼロ
　→ 電圧0Vの電圧源 = 導線（短絡）
• 理想電流源：内部抵抗無限大
　→ 電流0Aの電流源 = 断線（開放）

■ 問題の回路を重ね合わせで分解

元の回路（2つの電源がある）：

元の回路

これを2つに分解すると：

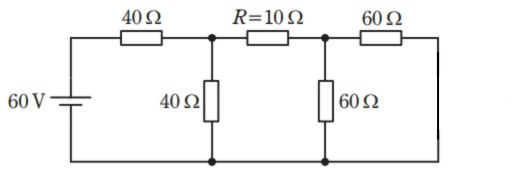
左の60V電源のみの回路（右の80V電源を短絡）

左電源のみ

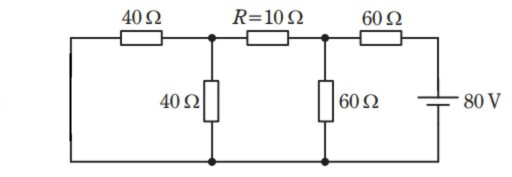
右の80V電源のみの回路（左の60V電源を短絡）

右電源のみ

■ 重ね合わせの理が使える条件

線形回路であること！

以下の要素のみで構成される回路：
• 線形抵抗（オームの法則に従う）
• 理想電圧源・電流源
• 線形インダクタンス・キャパシタンス

ダイオードやトランジスタなど非線形素子がある回路では使えません！

■ 電流の向きの取り方

重要なルール

1. 各電源単独の回路で電流の向きを仮定
2. 計算結果が正→仮定の向きが正しい
3. 計算結果が負→実際は逆向き
4. 最後に向きを考慮して加減算

分圧・分流の法則の理解と活用

分圧・分流の法則とは？

直列回路での電圧の分配（分圧）と、並列回路での電流の分配（分流）を簡単に計算できる法則です。複雑な回路計算を大幅に簡略化できる重要テクニックです！

■ 分圧の法則（直列回路）

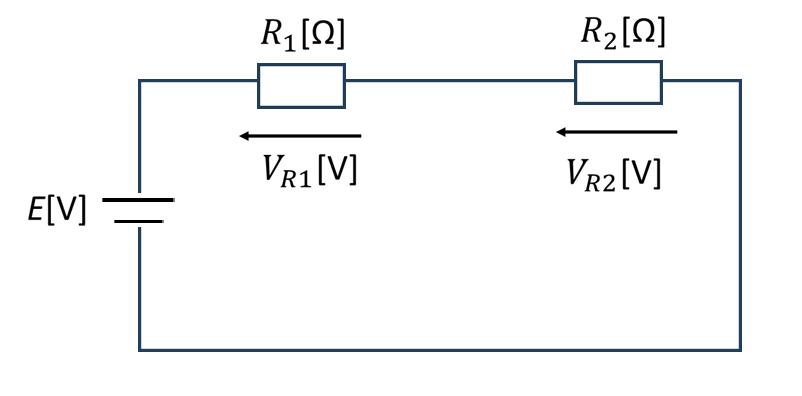
分圧の法則

基本公式

\[ V_{R1} = \frac{R_1}{R_1 + R_2} \times E \] \[ V_{R2} = \frac{R_2}{R_1 + R_2} \times E \]

覚え方：「自分の抵抗÷全抵抗×全電圧」

■ 分流の法則（並列回路）

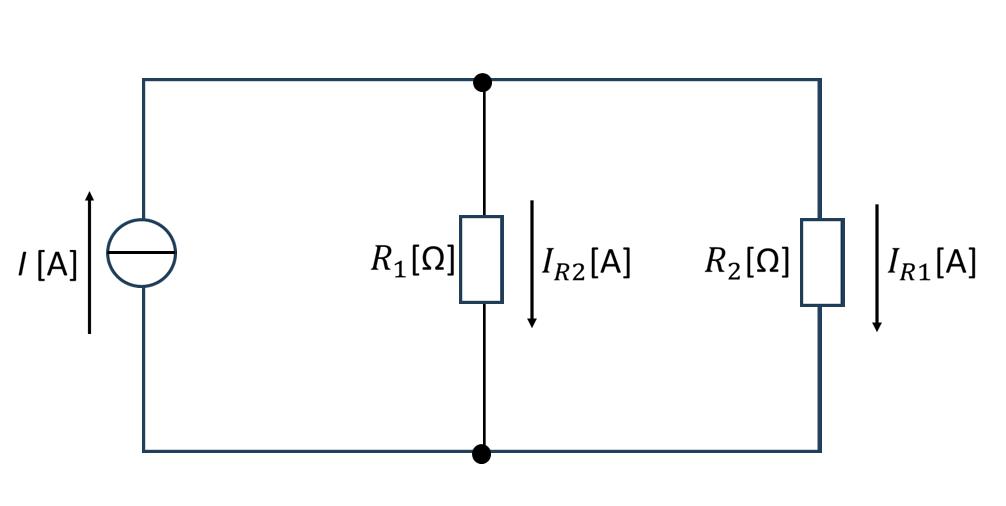
分流の法則

基本公式（要注意！）

\[ I_{R1} = \frac{\color{red}{R_2}}{R_1 + R_2} \times I \] \[ I_{R2} = \frac{\color{red}{R_1}}{R_1 + R_2} \times I \]

注意：分子が相手の抵抗！
覚え方：「相手の抵抗÷全抵抗×全電流」

■ なぜ分流では分子が逆になるの？

物理的な意味から理解

• 抵抗が小さい方に電流は多く流れる
• R₁が小さい → I₁が大きい
• でも式では分子にR₂が来る

理由：並列では電圧が同じ
V = R₁I₁ = R₂I₂
→ I₁/I₂ = R₂/R₁（反比例）

■ 実用的な覚え方

法則 覚え方 チェック方法
分圧 「自分/全体」 V₁ + V₂ = E になるか確認
分流 「相手/全体」 I₁ + I₂ = I になるか確認

■ 3つ以上の素子での分圧・分流

3つの抵抗の直列（分圧）

\[ V_{R1} = \frac{R_1}{R_1 + R_2 + R_3} \times E \]

3つの抵抗の並列（分流）

\[ I_{R1} = \frac{\frac{1}{R_1}}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} \times I \]

または合成抵抗を使って2段階で計算

■ よくある間違いと対策

間違いやすいポイント

• 分流で自分の抵抗を分子にする
　→ 必ず「相手の抵抗」を分子に！
• 単位を間違える
　→ kΩとΩを混在させない
• 部分的な分圧・分流
　→ どこからどこまでが対象か明確に

合成抵抗の計算テクニック

合成抵抗の基本

複数の抵抗を1つの等価な抵抗に置き換えることで、回路を簡単化できます。直列は足し算、並列は逆数の和の逆数というルールを確実に使いこなしましょう！

■ 直列合成抵抗

基本公式（単純な足し算）

\[ R_{合成} = R_1 + R_2 + R_3 + \cdots \]

理由：電流が同じで電圧が加算される

■ 並列合成抵抗

基本公式（逆数の和の逆数）

\[ \frac{1}{R_{合成}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots \]

2つの抵抗の場合の便利な公式

\[ R_{合成} = \frac{R_1 \times R_2}{R_1 + R_2} \]

「積÷和」と覚える！

■ 特殊なケースの合成抵抗

ケース 合成抵抗 覚え方
同じ抵抗R×2個（直列） 2R 2倍になる
同じ抵抗R×2個（並列） R/2 半分になる
同じ抵抗R×n個（直列） nR n倍になる
同じ抵抗R×n個（並列） R/n 1/nになる

■ Y-Δ変換（参考）

複雑な回路で使う変換

3つの抵抗がY型（スター）またはΔ型（デルタ）に接続されているとき、等価変換できます。
電験三種では基本的に出題されませんが、知っておくと便利です。

■ 合成抵抗計算の順序

効率的な計算手順

1. 回路図を整理（電源を基準に描き直す）
2. 最も遠い部分から合成開始
3. 並列→直列の順で計算が楽
4. 同じ値の抵抗は公式を活用
5. 最後に全体の合成抵抗を確認

■ 実際の計算例（問題から）

左側60V電源のみの回路での計算

1. 右側の60Ω×2個の並列：60/2 = 30Ω
2. 30ΩとR(10Ω)の直列：30+10 = 40Ω
3. 40Ωと左下40Ωの並列：40×40/(40+40) = 20Ω
4. 20Ωと左上40Ωの直列：20+40 = 60Ω（全体）

重ね合わせの理による実践的解法

問題を確実に解くための手順

2つの電源がある回路で、中央の抵抗R=10Ωで消費される電力を求めます。重ね合わせの理を使って、各電源による電流を別々に計算し、最後に合成します。

■ Step 1：回路を2つに分解

元の回路

元の回路

60V電源と80V電源、R=10Ωを含む複雑な回路

■ Step 2：左の60V電源のみの解析

右の80V電源を短絡した回路

左電源のみ

合成抵抗の計算

1. 右側60Ω×2の並列：30Ω
2. R(10Ω)と直列：40Ω
3. 左下40Ωと並列：20Ω
4. 左上40Ωと直列：60Ω（全体）

電流計算

• 電源電流：60V÷60Ω = 1A
• 分流でR通過分：40/(40+40)×1 = 0.5A

■ Step 3：右の80V電源のみの解析

左の60V電源を短絡した回路

右電源のみ

合成抵抗の計算

1. 左側40Ω×2の並列：20Ω
2. R(10Ω)と直列：30Ω
3. 右下60Ωと並列：20Ω
4. 右上60Ωと直列：80Ω（全体）

電流計算

• 電源電流：80V÷80Ω = 1A
• 分流でR通過分：60/(30+60)×1 = 0.667A

■ Step 4：電流の重ね合わせ

電流の向きに注意！

• 左60V電源による電流：0.5A（左→右）
• 右80V電源による電流：0.667A（右→左）

実際の電流（右→左を正）：
I = 0.667 - 0.5 = 0.167A

■ Step 5：消費電力の計算

電力の公式

\[ P = RI^2 = 10 \times 0.167^2 = 0.28 \text{ W} \]

答え：0.28W

■ 他の解法との比較

解法 メリット デメリット 適する問題
重ね合わせの理 理解しやすい
計算ミスを発見しやすい		 計算量が多い 電源が2～3個
キルヒホッフ 確実に解ける 連立方程式が必要 複雑な回路
テブナンの定理 特定素子の解析に便利 慣れが必要 1素子に注目
ミルマンの定理 並列電源で高速 適用条件が限定的 並列電源回路

■ よくある計算ミスと対策

注意すべきポイント

• 電源を除去する際の短絡・開放を間違えない
• 分流の公式で分子を間違えない（相手の抵抗！）
• 電流の向きを最後まで追跡する
• 小数の計算は最後にまとめて行う
• 単位（W、mW）を確認する

■ 試験での時間配分

効率的な解答方法

1. 回路図の整理：2分
2. 各電源の計算：各5分（計10分）
3. 重ね合わせと電力計算：3分
合計：15分程度で解答可能

🔍 ワンポイントアドバイス：重ね合わせの理は「電圧源は短絡、電流源は開放」が鉄則です！分流の法則では「相手の抵抗が分子」という点に特に注意しましょう。この問題のように2つの電源がある場合、各電源で別々に計算して最後に電流の向きを考慮して足し合わせます。計算は多いですが、一つ一つ確実に進めれば必ず解けます。練習を重ねて15分以内で解けるようになりましょう！

今日は直流回路の重ね合わせの理を使った問題やで！2つの電源がある回路で、抵抗 \( R = 10 \ \mathrm{\Omega} \) で消費される電力を求める問題や。これ、令和5年上期と平成25年にも全く同じ問題が出てるから、めっちゃ重要やねん。

2つの電源がある複雑な回路ですね。60Vと80Vの電源があって、それぞれ40Ωと60Ωの抵抗でつながっています。真ん中の10Ωの抵抗で消費される電力を求めるには、重ね合わせの理を使えばいいんですね。まず電源を1つずつ考えるということでしょうか？

その通りや！重ね合わせの理ってのはな、複数の電源がある回路を電源ごとに分解して計算する方法なんや。電圧源は短絡、電流源は開放にするんやで。

なるほど！つまり、まず左側の60V電源だけを考えて右側の80V電源を短絡した回路と、右側の80V電源だけを考えて左側の60V電源を短絡した回路の2つに分けるんですね。それぞれで10Ωに流れる電流を計算して、最後に重ね合わせるという流れですね。

完璧や！じゃあまず左の60V電源だけの回路から見ていこか。右の80V電源を短絡すると、こんな回路になるんや。

右側の電源を短絡すると、右側の60Ω抵抗2つが並列になってますね。この並列合成抵抗は \( \frac{60 \times 60}{60 + 60} = 30 \ \mathrm{\Omega} \) です。そして10Ωと直列になるから、合計で40Ωになります。さらにこれが左側の40Ωと並列になるという構造ですね。

よう計算できてるな！じゃあ続きの合成抵抗も計算してみよか。40Ωと40Ωの並列はどうなる？

40Ωと40Ωの並列合成抵抗は \( \frac{40 \times 40}{40 + 40} = 20 \ \mathrm{\Omega} \) になります。これに左上の40Ωが直列につながるので、電源から見た全体の抵抗は \( 20 + 40 = 60 \ \mathrm{\Omega} \) です。

したがって、電源から流れる電流は \( I_{v1} = \frac{60}{60} = 1 \ \mathrm{A} \) ですね。

ええ感じや！次は分流の法則を使って、10Ωに流れる電流を求めるで。並列回路での分流、覚えてるか？

分流の法則では、電流は抵抗に反比例して流れますね。10Ωを含む経路の抵抗は40Ω、もう一方も40Ωなので、1Aの電流は均等に分かれます。

つまり \( I_1 = \frac{40}{40 + 40} \times 1 = 0.5 \ \mathrm{A} \) が10Ωに流れます。電流の向きは左から右ですね。

完璧や！じゃあ今度は右の80V電源だけの回路を見てみよか。左の60V電源を短絡するとこうなるで。

今度は左側の40Ω抵抗2つが並列になって \( \frac{40}{2} = 20 \ \mathrm{\Omega} \) になりますね。これに10Ωが直列だから合計30Ω。この30Ωが右側の60Ωと並列になります。

並列合成抵抗は \( \frac{30 \times 60}{30 + 60} = 20 \ \mathrm{\Omega} \) で、右上の60Ωと直列だから全体は80Ωです。

ばっちりやな！電源から流れる電流と、10Ωに流れる電流も計算してみよか。

電源から流れる電流は \( I_{v2} = \frac{80}{80} = 1 \ \mathrm{A} \) です。

分流の法則より、10Ωを含む経路（30Ω）には \( I_2 = \frac{60}{30 + 60} \times 1 = \frac{2}{3} \approx 0.667 \ \mathrm{A} \) が流れます。

この電流は右から左に流れますね。

よし！ここからが重要やで。2つの電流の向きに注意して重ね合わせるんや。電流の向きはどうなってる？

左の電源による電流 \( I_1 = 0.5 \ \mathrm{A} \) は左から右へ、右の電源による電流 \( I_2 = 0.667 \ \mathrm{A} \) は右から左へ流れています。

向きが逆なので、実際に10Ωに流れる電流は \( I = I_2 - I_1 = 0.667 - 0.5 = 0.167 \ \mathrm{A} \) で、右から左へ流れることになります。

その通りや！最後に消費電力を計算するで。電力の公式は3つあるけど、どれ使う？

電力の公式は \( P = VI \)、\( P = RI^2 \)、\( P = \frac{V^2}{R} \) の3つがありますが、抵抗値と電流が分かっているので \( P = RI^2 \) を使います。

\( P = 10 \times 0.167^2 = 10 \times 0.0279 = 0.279 \approx 0.28 \ \mathrm{W} \)

答えは(1)の0.28Wですね！

完璧や！ところで、なんで \( P = RI^2 \) を選んだか分かるか？実はこれ、試験のテクニックでもあるんやで。

抵抗で消費される電力を求める問題では、抵抗値は必ず与えられています。今回は電流を求めたので \( P = RI^2 \) が最も簡単ですね。

もし電圧を求めていたら \( P = \frac{V^2}{R} \) を使う方が早いということですね。計算の手間を減らすことで、ミスも減らせます。

そうやそうや！実際の現場でもこの重ね合わせの理はよく使うんやで。例えば、複数の発電機がつながってる系統とかな。

確かに実際の電力系統では、複数の発電所から電力が供給されていますよね。事故解析や潮流計算でも、重ね合わせの理の考え方が基礎になっているんでしょうね。

電験三種でこの問題が繰り返し出題されるのも、実務で重要だからですね。

最後に、この問題のポイントをまとめとこか。試験で似た問題が出たときの対策にもなるで！

重ね合わせの理を使う問題のポイント：

1. 電源を1つずつ考え、他は短絡（電圧源）か開放（電流源）

2. 合成抵抗を丁寧に計算（並列→直列の順番に注意）

3. 分流の法則では分母が逆になることに注意

4. 電流の向きを考慮して重ね合わせ

5. 電力計算は適切な公式を選択

これで類題にも対応できますね！

解説まとめ

■ 重ね合わせの理とは

重ね合わせの理（重ね合わせの原理）は、複数の電源を含む線形回路において、各電源が単独で存在する場合の電流・電圧を個別に計算し、それらを重ね合わせることで全体の電流・電圧を求める解析手法です。計算時は、着目する電源以外の電圧源は短絡、電流源は開放として扱います。複雑な回路を単純な回路の組み合わせとして解析できるため、電気主任技術者試験で頻出の重要な手法です。

問題回路図

■ 計算手順と公式

  1. 重ね合わせの理の適用

    複数電源回路を電源ごとに分解し、個別に解析します。

    ・電圧源は短絡として扱う

    ・電流源は開放として扱う

  2. 合成抵抗の計算

    直列合成抵抗：

    \( R = R_1 + R_2 \)

    並列合成抵抗：

    \( R = \frac{R_1 R_2}{R_1 + R_2} \)

  3. 分流の法則

    並列回路での電流分配：

    \( I_{R1} = \frac{R_2}{R_1 + R_2} \times I \)

    ※分母は抵抗の和、分子は相手側の抵抗値

    分流の法則
  4. 分圧の法則

    直列回路での電圧分配：

    \( V_{R1} = \frac{R_1}{R_1 + R_2} \times V \)

    分圧の法則

■ 具体的な計算例

問題条件

  • 左側電源：\( V_1 = 60 \ \mathrm{V} \)
  • 右側電源：\( V_2 = 80 \ \mathrm{V} \)
  • 中央の抵抗：\( R = 10 \ \mathrm{\Omega} \)
  • 左側の抵抗：\( R_1 = 40 \ \mathrm{\Omega} \)
  • 右側の抵抗：\( R_2 = 60 \ \mathrm{\Omega} \)

【Step 1】60V電源のみの場合（80V電源を短絡）

左側電源のみの回路

① 右側の並列抵抗の合成：

\[ \begin{aligned} R_2' &= \frac{R_2 \times R_2}{R_2 + R_2} = \frac{60 \times 60}{60 + 60} \\[5pt] &= \frac{60}{2} = 30 \ \mathrm{[\Omega]} \end{aligned} \]

② R と R₂' の直列合成：

\[ \begin{aligned} R' &= R + R_2' = 10 + 30 = 40 \ \mathrm{[\Omega]} \end{aligned} \]

③ R' と左側 R₁ の並列合成：

\[ \begin{aligned} R_1' &= \frac{R' \times R_1}{R' + R_1} = \frac{40 \times 40}{40 + 40} \\[5pt] &= 20 \ \mathrm{[\Omega]} \end{aligned} \]

④ 電源電流の計算：

\[ \begin{aligned} I_{v1} &= \frac{V_1}{R_1' + R_1} = \frac{60}{20 + 40} \\[5pt] &= 1 \ \mathrm{[A]} \end{aligned} \]

⑤ 抵抗 R を流れる電流（分流の法則）：

\[ \begin{aligned} I_1 &= \frac{R_1}{R' + R_1} \times I_{v1} = \frac{40}{40 + 40} \times 1 \\[5pt] &= 0.5 \ \mathrm{[A]} \end{aligned} \]

【Step 2】80V電源のみの場合（60V電源を短絡）

右側電源のみの回路

① 左側の並列抵抗の合成：

\[ \begin{aligned} R_1'' &= \frac{R_1 \times R_1}{R_1 + R_1} = \frac{40 \times 40}{40 + 40} \\[5pt] &= \frac{40}{2} = 20 \ \mathrm{[\Omega]} \end{aligned} \]

② R と R₁'' の直列合成：

\[ \begin{aligned} R'' &= R + R_1'' = 10 + 20 = 30 \ \mathrm{[\Omega]} \end{aligned} \]

③ R'' と右側 R₂ の並列合成：

\[ \begin{aligned} R_2'' &= \frac{R'' \times R_2}{R'' + R_2} = \frac{30 \times 60}{30 + 60} \\[5pt] &= 20 \ \mathrm{[\Omega]} \end{aligned} \]

④ 電源電流の計算：

\[ \begin{aligned} I_{v2} &= \frac{V_2}{R_2'' + R_2} = \frac{80}{20 + 60} \\[5pt] &= 1 \ \mathrm{[A]} \end{aligned} \]

⑤ 抵抗 R を流れる電流（分流の法則）：

\[ \begin{aligned} I_2 &= \frac{R_2}{R'' + R_2} \times I_{v2} = \frac{60}{30 + 60} \times 1 \\[5pt] &= \frac{2}{3} \approx 0.6667 \ \mathrm{[A]} \end{aligned} \]

【Step 3】重ね合わせと電力計算

抵抗 R を流れる正味の電流（電流の向きに注意）：

\[ \begin{aligned} I &= I_2 - I_1 = 0.6667 - 0.5 \\[5pt] &= 0.1667 \ \mathrm{[A]} \end{aligned} \]

抵抗 R で消費される電力：

\[ \begin{aligned} P &= R \times I^2 = 10 \times (0.1667)^2 \\[5pt] &= 10 \times 0.0278 \\[5pt] &\approx 0.28 \ \mathrm{[W]} \end{aligned} \]

結論：抵抗 R = 10Ω で消費される電力は 0.28 W（選択肢(1)）

■ 実務上の留意点

重ね合わせの理を用いた回路解析において、以下の点に注意が必要です。