第三種電気主任技術者試験(電験三種)
直流回路学習ページ
オームの法則から始まり、複雑な回路網の解析まで、論理的思考と数学的手法を身につけていきましょう。
第1節 電気回路の基礎
1. 電気回路とは
電気回路とは、電気エネルギーを伝達・変換・制御するために、電気的素子(抵抗、コンデンサ、コイル、電源など)を導線で接続して構成したものです。私たちの身の回りにある電化製品は、すべて電気回路によって動作しています。スマートフォンの充電器、電気ポット、エアコン、LED照明など、現代生活は電気回路なしには成り立ちません。
電気回路を理解するためには、まず基本的な概念を整理する必要があります。電気回路における基本的な物理量として、電圧(V)、電流(I)、抵抗(R)があります。これらの関係を表すオームの法則は、電気回路解析の根幹をなす最も重要な法則です。
電気回路の基本的な構成要素について詳しく見てみましょう。電源は電気エネルギーを供給する部分で、乾電池、蓄電池、発電機などがあります。負荷は電気エネルギーを消費する部分で、電灯、モータ、ヒータなどがこれにあたります。導線は電流を流すための経路で、通常は銅線が使用されます。
電気回路には直流回路と交流回路の2つの基本的な種類があります。直流(DC: Direct Current)は、電流の大きさと方向が時間とともに変化しない電流です。乾電池や蓄電池から得られる電流がこれにあたります。一方、交流(AC: Alternating Current)は、電流の大きさと方向が周期的に変化する電流で、家庭用コンセントから供給される電力がこれにあたります。
- オームの法則:V = IR(電圧 = 電流 × 抵抗)
- キルヒホッフの電流則:節点に流入する電流の総和 = 流出する電流の総和
- キルヒホッフの電圧則:閉回路における電圧降下の総和 = 起電力の総和
- ジュールの法則:P = I²R(電力 = 電流の2乗 × 抵抗)
2. オームの法則
オームの法則は、1827年にドイツの物理学者ゲオルク・ジーモン・オーム(Georg Simon Ohm)によって発見された、電気回路における最も基本的で重要な法則です。この法則は、導体における電圧、電流、抵抗の関係を定量的に表現しており、すべての電気回路解析の基礎となっています。
オームの法則は、「導体に流れる電流は、その両端に加えられた電圧に比例し、導体の抵抗に反比例する」と表現されます。これを数式で表すと、V = IR となります。この単純な式が、複雑な電気回路の解析から電気機器の設計まで、あらゆる電気工学の分野で活用されています。
V:電圧[V]、I:電流[A]、R:抵抗[Ω]
オームの法則を理解するために、水の流れとの類推を考えてみましょう。電圧は水圧に、電流は水の流れる量に、抵抗は配管の太さや長さによる流れにくさに対応します。水圧が高いほど多くの水が流れ、配管が細いほど流れにくくなるのと同様に、電圧が高いほど多くの電流が流れ、抵抗が大きいほど電流は流れにくくなります。
12Vの電源に20Ωの抵抗を接続した。この回路に流れる電流と、抵抗で消費される電力を求めよ。
解答:
電流を求める:
\[ \begin{aligned} I &= \frac{V}{R} \\[10pt] &= \frac{12}{20} \\[10pt] &= 0.6 \quad \mathrm{[A]} \end{aligned} \]電力を求める:
\[ \begin{aligned} P &= V \times I \\[10pt] &= 12 \times 0.6 \\[10pt] &= 7.2 \quad \mathrm{[W]} \end{aligned} \]オームの法則には重要な適用条件があります。この法則は、温度が一定で、線形な抵抗素子(オーム性素子)にのみ適用されます。半導体素子やガス放電管などの非線形素子では、オームの法則は成り立ちません。また、温度が変化すると抵抗値も変化するため、厳密にはオームの法則の適用には注意が必要です。
実用的な観点から、オームの法則は電気回路の設計や故障診断において極めて重要です。例えば、LED照明の設計では、LEDに適切な電流を流すために必要な抵抗値をオームの法則で計算します。また、電気機器の故障診断では、予想される電圧・電流値と実測値を比較することで、異常箇所を特定できます。
12Vの電源を使って、定格電流20mAのLEDを点灯させたい。必要な制限抵抗の値を求めよ。(LEDの順方向電圧を2Vとする)
解答:
制限抵抗にかかる電圧:
\[ \begin{aligned} V_R &= V_{電源} - V_{LED} \\[10pt] &= 12 - 2 \\[10pt] &= 10 \quad \mathrm{[V]} \end{aligned} \]必要な抵抗値:
\[ \begin{aligned} R &= \frac{V_R}{I} \\[10pt] &= \frac{10}{0.02} \\[10pt] &= 500 \quad \mathrm{[Ω]} \end{aligned} \]3. 抵抗の直列接続
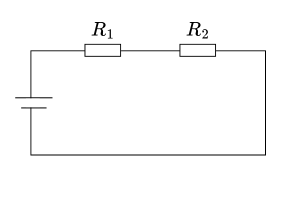
抵抗の直列接続は、複数の抵抗を一列に並べて接続する方法です。直列接続された抵抗には同じ電流が流れ、各抵抗での電圧降下の合計が電源電圧に等しくなります。この接続方法は、電圧分割回路や電流制限回路として広く使用されています。
直列接続の最も重要な特徴は、合成抵抗が各抵抗の単純な和になることです。これは、電流が各抵抗を順番に通過するため、それぞれの抵抗による電圧降下が累積されるためです。2つの抵抗 \(R_1\) と \(R_2\) を直列接続した場合、合成抵抗 \(R_t\) は次のように表されます。
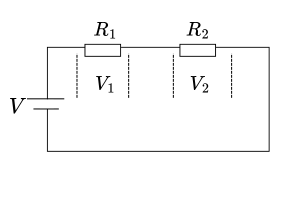
直列接続における電圧分割の原理は、電子回路設計において極めて重要です。各抵抗にかかる電圧は、その抵抗値に比例して配分されます。これを利用して、所望の電圧を得る電圧分割回路を構成できます。
24Vの電源に、\(R_1 = 100Ω\)、\(R_2 = 200Ω\)、\(R_3 = 300Ω\) の抵抗を直列接続した。
(1) 合成抵抗
(2) 回路に流れる電流
(3) 各抵抗にかかる電圧
解答:
(1) 合成抵抗:
\[ \begin{aligned} R_t &= R_1 + R_2 + R_3 \\[10pt] &= 100 + 200 + 300 \\[10pt] &= 600 \quad \mathrm{[Ω]} \end{aligned} \](2) 回路電流:
\[ \begin{aligned} I &= \frac{V}{R_t} \\[10pt] &= \frac{24}{600} \\[10pt] &= 0.04 \quad \mathrm{[A]} = 40 \quad \mathrm{[mA]} \end{aligned} \](3) 各抵抗の電圧:
\[ \begin{aligned} V_1 &= I \times R_1 = 0.04 \times 100 = 4 \quad \mathrm{[V]} \\[10pt] V_2 &= I \times R_2 = 0.04 \times 200 = 8 \quad \mathrm{[V]} \\[10pt] V_3 &= I \times R_3 = 0.04 \times 300 = 12 \quad \mathrm{[V]} \\[10pt] \text{検算:} \quad &V_1 + V_2 + V_3 = 4 + 8 + 12 = 24 \quad \mathrm{[V]} ✓ \end{aligned} \]直列接続の実用例として、ボリューム(可変抵抗器)があります。ボリュームは抵抗体に可動接点を持つ素子で、音響機器の音量調節に使用されます。全抵抗値が一定で、可動接点の位置により出力電圧が連続的に変化する電圧分割回路として機能します。
4. 抵抗の並列接続
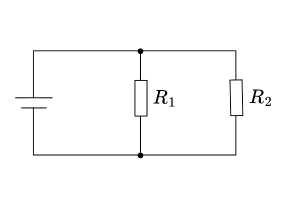
抵抗の並列接続は、複数の抵抗の両端を共通の点で接続する方法です。並列接続された各抵抗には同じ電圧が加わり、各抵抗に流れる電流の合計が全電流になります。この接続方法は、電流分割回路や負荷の冗長化に使用されます。
並列接続の合成抵抗は、各抵抗の逆数の和の逆数として求められます。これは、並列接続により電流の通り道が増えるため、全体として抵抗が小さくなることを表しています。並列接続の合成抵抗は、常に最小の抵抗値よりも小さくなります。
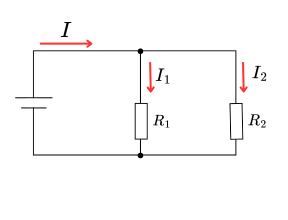
並列接続における電流分割の原理も重要です。各抵抗に流れる電流は、その抵抗値に反比例します。抵抗が小さいほど多くの電流が流れ、抵抗が大きいほど少ない電流が流れます。この性質を利用して、電流計の測定範囲を拡大する分流器が作られています。
12Vの電源に、\(R_1 = 60Ω\)、\(R_2 = 30Ω\)、\(R_3 = 20Ω\) の抵抗を並列接続した。
(1) 合成抵抗
(2) 各抵抗に流れる電流
(3) 電源から供給される全電流
解答:
(1) 合成抵抗:
\[ \begin{aligned} \frac{1}{R_t} &= \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \\[10pt] &= \frac{1}{60} + \frac{1}{30} + \frac{1}{20} \\[10pt] &= \frac{1 + 2 + 3}{60} = \frac{6}{60} = \frac{1}{10} \\[10pt] R_t &= 10 \quad \mathrm{[Ω]} \end{aligned} \](2) 各抵抗の電流:
\[ \begin{aligned} I_1 &= \frac{V}{R_1} = \frac{12}{60} = 0.2 \quad \mathrm{[A]} \\[10pt] I_2 &= \frac{V}{R_2} = \frac{12}{30} = 0.4 \quad \mathrm{[A]} \\[10pt] I_3 &= \frac{V}{R_3} = \frac{12}{20} = 0.6 \quad \mathrm{[A]} \end{aligned} \](3) 全電流:
\[ \begin{aligned} I &= I_1 + I_2 + I_3 \\[10pt] &= 0.2 + 0.4 + 0.6 \\[10pt] &= 1.2 \quad \mathrm{[A]} \end{aligned} \]検算(オームの法則):
\[I = \frac{V}{R_t} = \frac{12}{10} = 1.2 \quad \mathrm{[A]} ✓\]並列接続の実用例として、家庭用配線があります。各部屋の照明やコンセントは並列接続されており、一つの機器が故障しても他の機器は正常に動作します。また、自動車のヘッドライトも左右が並列接続されており、一方が切れても他方は点灯し続けます。
5. 複合回路の解析
複合回路とは、直列接続と並列接続が組み合わされた回路のことです。実際の電気回路では、単純な直列や並列接続だけでなく、これらが複雑に組み合わされることが一般的です。複合回路の解析には、基本的な直列・並列の公式を段階的に適用していく方法が有効です。
複合回路を解析する際の基本的な手順は以下の通りです: 1. 回路図を詳しく観察し、直列部分と並列部分を識別する 2. 最も内側(電源から遠い部分)から順に合成抵抗を計算する 3. 合成された抵抗を一つの抵抗として扱い、段階的に簡単化する 4. 最終的に得られた合成抵抗を用いて全電流を求める 5. 逆算により各部分の電圧・電流を求める
図に示す回路において、各抵抗に流れる電流を求めよ。
\(R_1 = 10Ω\)、\(R_2 = 20Ω\)、\(R_3 = 30Ω\)、\(R_4 = 15Ω\)、\(V = 24V\)
(\(R_2\)と\(R_3\)が並列、これと\(R_1\)、\(R_4\)が直列接続)
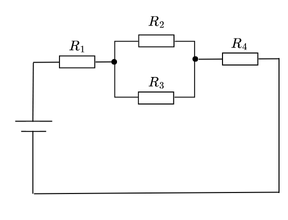
解答:
ステップ1:\(R_2\)と\(R_3\)の並列合成抵抗:
\[ \begin{aligned} R_{23} &= \frac{R_2 \times R_3}{R_2 + R_3} \\[10pt] &= \frac{20 \times 30}{20 + 30} \\[10pt] &= \frac{600}{50} = 12 \quad \mathrm{[Ω]} \end{aligned} \]ステップ2:全体の合成抵抗:
\[ \begin{aligned} R_t &= R_1 + R_{23} + R_4 \\[10pt] &= 10 + 12 + 15 \\[10pt] &= 37 \quad \mathrm{[Ω]} \end{aligned} \]ステップ3:主回路電流:
\[ \begin{aligned} I &= \frac{V}{R_t} \\[10pt] &= \frac{24}{37} \\[10pt] &≈ 0.649 \quad \mathrm{[A]} \end{aligned} \]ステップ4:\(R_{23}\)にかかる電圧:
\[ \begin{aligned} V_{23} &= I \times R_{23} \\[10pt] &= 0.649 \times 12 \\[10pt] &≈ 7.78 \quad \mathrm{[V]} \end{aligned} \]ステップ5:\(R_2\)、\(R_3\)の各電流:
\[ \begin{aligned} I_2 &= \frac{V_{23}}{R_2} = \frac{7.78}{20} ≈ 0.389 \quad \mathrm{[A]} \\[10pt] I_3 &= \frac{V_{23}}{R_3} = \frac{7.78}{30} ≈ 0.259 \quad \mathrm{[A]} \\[10pt] I_1 = I_4 &= I = 0.649 \quad \mathrm{[A]} \end{aligned} \]6. 電池の接続方法
電池の接続方法には、直列接続、並列接続、および直並列接続があります。それぞれの接続方法により、出力電圧、電流供給能力、持続時間などの特性が変化します。実用的な電池パックでは、用途に応じてこれらの接続方法を組み合わせて使用します。
電池の直列接続では、各電池の起電力が加算され、より高い電圧を得ることができます。例えば、1.5Vの乾電池を4個直列接続すると6Vの電源となります。しかし、電流供給能力は1個の電池と同じです。また、1個の電池が劣化すると全体の性能が低下するという欠点があります。
電池の並列接続では、起電力は1個の電池と同じですが、電流供給能力が向上し、動作時間が延長されます。また、1個の電池が故障しても他の電池で動作を継続できるという利点があります。ただし、電池の特性が揃っていないと、電池間で電流のやり取りが生じ、効率が低下する可能性があります。
起電力1.5V、内部抵抗0.1Ωの乾電池6個を使用して、3Vの電源を作りたい。
(1) 直列接続の場合の特性
(2) 2個直列×3組並列の場合の特性
(3) 負荷抵抗2.8Ωを接続した時の出力電流
解答:
(1) 直列接続(6個):
\[ \begin{aligned} E_t &= 6 \times 1.5 = 9 \quad \mathrm{[V]} \\[10pt] r_t &= 6 \times 0.1 = 0.6 \quad \mathrm{[Ω]} \end{aligned} \]→3Vにならないため不適切
(2) 2個直列×3組並列:
\[ \begin{aligned} E_t &= 2 \times 1.5 = 3 \quad \mathrm{[V]} \\[10pt] r_t &= \frac{2 \times 0.1}{3} = \frac{0.2}{3} ≈ 0.067 \quad \mathrm{[Ω]} \end{aligned} \](3) 負荷電流:
\[ \begin{aligned} I &= \frac{E_t}{r_t + R_L} \\[10pt] &= \frac{3}{0.067 + 2.8} \\[10pt] &= \frac{3}{2.867} ≈ 1.05 \quad \mathrm{[A]} \end{aligned} \]7. キルヒホッフの法則
キルヒホッフの法則は、ドイツの物理学者グスタフ・キルヒホッフ(Gustav Kirchhoff)によって1845年に発表された、電気回路解析の基本法則です。この法則は、オームの法則だけでは解析困難な複雑な回路網を体系的に解析するための強力な手法を提供します。キルヒホッフの法則には、電流則(第1法則)と電圧則(第2法則)の2つがあります。
キルヒホッフの電流則(KCL: Kirchhoff's Current Law)は、「任意の節点(接続点)において、流入する電流の総和と流出する電流の総和は等しい」という法則です。これは電荷保存の法則に基づいており、電流の連続性を表現しています。数式では、節点における電流の代数和は零であると表現されます。
または、流入を正、流出を負として:
\[ \sum I = 0 \]キルヒホッフの電圧則(KVL: Kirchhoff's Voltage Law)は、「任意の閉回路において、起電力の総和と電圧降下の総和は等しい」という法則です。これはエネルギー保存の法則に基づいており、閉回路を一周した時の電位変化の総和が零であることを表現しています。
または、一方向に回った時:
\[ \sum E - \sum IR = 0 \]図に示す回路において、各枝路の電流を求めよ。
\(E_1 = 12V\)、\(E_2 = 6V\)、\(R_1 = 2Ω\)、\(R_2 = 3Ω\)、\(R_3 = 6Ω\)
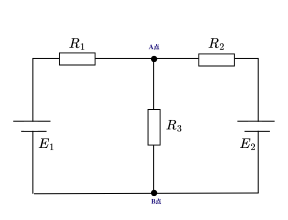
解答:
ステップ1:電流の方向を仮定
\(I_1\):\(R_1\)を流れる電流(右向き)
\(I_2\):\(R_2\)を流れる電流(右向き)
\(I_3\):\(R_3\)を流れる電流(下向き)
ステップ2:節点Aでの電流則
\[I_1 = I_2 + I_3 \quad \cdots (1)\]ステップ3:左ループでの電圧則
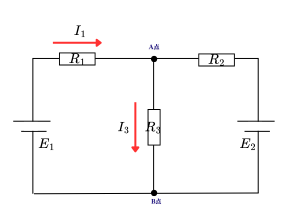
ステップ4:右ループでの電圧則
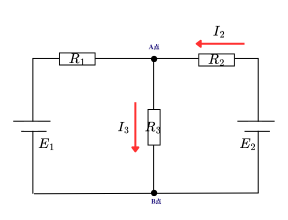
ステップ5:連立方程式を解く
式(1)を式(2)に代入:
\[ \begin{aligned} 12 &= 2(I_2 + I_3) + 6I_3 \\[10pt] 12 &= 2I_2 + 8I_3 \quad \cdots (4) \end{aligned} \]式(3)から:
\[I_2 = 2I_3 - 2 \quad \cdots (5)\]式(5)を式(4)に代入:
\[ \begin{aligned} 12 &= 2(2I_3 - 2) + 8I_3 \\[10pt] 12 &= 4I_3 - 4 + 8I_3 \\[10pt] 16 &= 12I_3 \\[10pt] I_3 &= \frac{4}{3} \quad \mathrm{[A]} \end{aligned} \]各電流値:
\[ \begin{aligned} I_3 &= \frac{4}{3} = 1.33 \quad \mathrm{[A]} \\[10pt] I_2 &= 2 \times \frac{4}{3} - 2 = \frac{2}{3} = 0.67 \quad \mathrm{[A]} \\[10pt] I_1 &= I_2 + I_3 = \frac{2}{3} + \frac{4}{3} = 2 \quad \mathrm{[A]} \end{aligned} \]キルヒホッフの法則は、電気回路の設計や故障診断において極めて実用的です。例えば、配電系統の負荷分散計算、電子回路の動作点解析、太陽電池パネルの直並列接続設計など、様々な分野で応用されています。また、コンピュータを用いた回路シミュレーションソフトウェアも、基本的にはキルヒホッフの法則に基づいて動作しています。
- 電流の方向:任意に設定し、負の値が出れば逆方向
- 電圧の極性:一定の規則で統一する(時計回りなど)
- 独立方程式:n個の未知数にはn個の独立した方程式が必要
- 検算の重要性:求めた解が各法則を満たすか確認
- オームの法則:V = IR、電気回路解析の基礎
- 直列接続:抵抗加算、電圧分割、電流共通
- 並列接続:抵抗逆数加算、電流分割、電圧共通
- 複合回路:段階的簡略化による解析
- 電池接続:直列で電圧増加、並列で電流増加
- キルヒホッフの法則:電流則(節点)、電圧則(閉回路)
- 公式の暗記:オームの法則、合成抵抗の公式
- 単位の換算:mA⇔A、kΩ⇔Ω、MΩ⇔Ω
- 計算精度:有効数字、小数点以下の桁数に注意
- 回路図の読解:直列・並列の判別、節点の特定
- 検算の習慣:キルヒホッフの法則による確認
- 実用問題:LED回路、分圧回路、電池の寿命計算
| 接続方法 | 合成抵抗 | 電流分布 | 電圧分布 | 用途例 |
|---|---|---|---|---|
| 直列 | \(R_1 + R_2\) | 各部共通 | 抵抗比に応じて分割 | 電圧分割、電流制限 |
| 並列 | \(\frac{R_1 R_2}{R_1 + R_2}\) | 抵抗に反比例して分割 | 各部共通 | 電流分割、冗長化 |
第2節 電力と熱エネルギー
1. 電流による発熱作用
電流が導体を流れると、導体の電気抵抗により電気エネルギーが熱エネルギーに変換されます。この現象は「ジュール熱」または「抵抗損失」と呼ばれ、1841年にイギリスの物理学者ジェームズ・プレスコット・ジュール(James Prescott Joule)によって定量的に解明されました。この発熱作用は、電気ヒータや白熱電球などで有効利用される一方で、送電線や電子機器では損失として問題となります。
電流による発熱の物理的メカニズムを理解してみましょう。導体内の自由電子が電界によって加速されると、原子核や他の電子との衝突により運動エネルギーを失います。この失われた運動エネルギーが熱エネルギーとして導体に蓄積され、温度上昇を引き起こします。抵抗が大きいほど、また電流が大きいほど、より多くの衝突が発生し、発熱量が増加します。
ジュール熱の発生量は、電流の2乗に比例することが重要なポイントです。これは、電流が2倍になると発熱量は4倍になることを意味します。この性質により、高電圧・低電流の送電方式が採用されており、送電効率の向上が図られています。例えば、同じ電力を送電する場合、電圧を10倍にして電流を1/10にすると、送電線での損失は1/100に削減できます。
H:発熱量[J]、I:電流[A]、R:抵抗[Ω]、V:電圧[V]、t:時間[s]
100Vの電源に接続された抵抗50Ωの電気ヒータを30分間使用した。
(1) ヒータに流れる電流
(2) 消費電力
(3) 発生する熱量(カロリー換算も含む)
解答:
(1) ヒータ電流:
\[ \begin{aligned} I &= \frac{V}{R} \\[10pt] &= \frac{100}{50} \\[10pt] &= 2 \quad \mathrm{[A]} \end{aligned} \](2) 消費電力:
\[ \begin{aligned} P &= V \times I \\[10pt] &= 100 \times 2 \\[10pt] &= 200 \quad \mathrm{[W]} \end{aligned} \](3) 発生熱量:
\[ \begin{aligned} t &= 30 \times 60 = 1800 \quad \mathrm{[s]} \\[10pt] H &= P \times t \\[10pt] &= 200 \times 1800 \\[10pt] &= 360,000 \quad \mathrm{[J]} = 360 \quad \mathrm{[kJ]} \end{aligned} \]カロリー換算(1cal = 4.18J):
\[ \begin{aligned} H &= \frac{360,000}{4.18} \\[10pt] &≈ 86,124 \quad \mathrm{[cal]} ≈ 86.1 \quad \mathrm{[kcal]} \end{aligned} \]電流による発熱の実用例は多岐にわたります。電気ストーブ、オーブン、電気ポットなどの加熱機器では、この原理を積極的に利用しています。一方、モータや変圧器では、巻線の抵抗による発熱は損失となるため、効率向上のために銅損(巻線での損失)の削減が重要な設計課題となります。
電子機器における発熱問題も重要です。CPUやパワー半導体では、高密度で電流が流れるため大量の熱が発生します。この熱を適切に放散しないと、素子の性能劣化や破損につながります。そのため、ヒートシンク、ファン、熱伝導材料などを用いた冷却技術が不可欠となっています。
- 電流の2乗比例:電流が2倍になると発熱は4倍
- 抵抗に比例:抵抗が大きいほど発熱量増加
- 時間に比例:使用時間が長いほど総発熱量増加
- 熱の蓄積:連続使用により温度が上昇し続ける
2. 電力および電力量
電力(Power)は単位時間あたりに消費または供給される電気エネルギーの量を表し、電力量(Electric Energy)は一定時間に消費または供給された電気エネルギーの総量を表します。この区別は、電気料金の計算や電気機器の性能評価において極めて重要です。電力の単位はワット[W]、電力量の単位はワット時[Wh]またはジュール[J]で表されます。
電力の基本概念を理解するために、機械的な仕事との類推を考えてみましょう。重い物を持ち上げる際、どれくらいの力でどれくらいの速さで持ち上げるかが仕事率(パワー)に相当し、最終的にどれくらいの高さまで持ち上げたかが仕事量に相当します。電気回路では、電圧が「力」、電流が「速さ」、電力が「仕事率」、電力量が「仕事量」に対応します。
W:電力量[Wh]、P:電力[W]、t:時間[h]
電力量の単位換算は実用上重要です。電力会社では通常kWh(キロワット時)を単位として電気料金を計算します。1kWh = 1000Wh = 3,600,000J = 3.6MJ の関係があります。家庭用電力メータは、この電力量を積算して表示しています。
以下の電気機器を1日使用した場合の電力量と電気料金を計算せよ。
- エアコン:1200W、8時間使用
- 冷蔵庫:150W、24時間使用
- LED照明:60W、6時間使用
(電気料金単価:27円/kWh)
解答:
各機器の電力量:
\[ \begin{aligned} W_{エアコン} &= 1200 \times 8 = 9600 \quad \mathrm{[Wh]} = 9.6 \quad \mathrm{[kWh]} \\[10pt] W_{冷蔵庫} &= 150 \times 24 = 3600 \quad \mathrm{[Wh]} = 3.6 \quad \mathrm{[kWh]} \\[10pt] W_{照明} &= 60 \times 6 = 360 \quad \mathrm{[Wh]} = 0.36 \quad \mathrm{[kWh]} \end{aligned} \]総電力量:
\[ \begin{aligned} W_{合計} &= 9.6 + 3.6 + 0.36 \\[10pt] &= 13.56 \quad \mathrm{[kWh]} \end{aligned} \]電気料金:
\[ \begin{aligned} \text{料金} &= 13.56 \times 27 \\[10pt] &= 366.12 \quad \mathrm{[円]} \end{aligned} \]電力効率の概念も重要です。効率 \(\eta\) は、有効に利用される電力と入力電力の比で定義されます。白熱電球の効率は約5%(残り95%は熱として放散)、LED照明は約20%、モータは90%以上の高効率を実現しています。効率向上は省エネルギーと環境負荷軽減の観点から極めて重要な技術課題です。
3. 温度上昇と許容電流
電気導体に電流が流れると、ジュール熱により導体の温度が上昇します。この温度上昇は、導体の材料特性、周囲環境、冷却条件などに依存します。導体の温度が過度に上昇すると、絶縁材料の劣化、導体の機械的強度低下、火災の危険性などが生じるため、許容温度以下に抑制する必要があります。
導体の温度上昇は、発生する熱量と放散する熱量のバランスによって決まります。定常状態では、ジュール熱による発熱量と、対流・輻射・伝導による放熱量が等しくなります。導体の太さ(断面積)、材質、周囲の冷却条件を適切に設計することで、許容温度以下に温度上昇を抑制できます。
電線の許容電流は、日本工業規格(JIS)や電気設備技術基準で規定されています。例えば、600V以下の配線用電線では、導体温度を60℃以下に抑制するよう定められています。電線サイズ(スケア)が大きいほど、断面積が増加して抵抗が減少し、より多くの電流を流すことができます。
長さ100m、断面積2.0mm²の銅導線(抵抗率 1.7×10⁻⁸Ω·m)に10Aの電流を流した。
(1) 導線の抵抗値
(2) 1時間あたりの発熱量
(3) 温度上昇(熱容量を無視し、放熱を考慮しない場合)
解答:
(1) 導線抵抗:
\[ \begin{aligned} R &= \rho \times \frac{l}{A} \\[10pt] &= 1.7 \times 10^{-8} \times \frac{100}{2.0 \times 10^{-6}} \\[10pt] &= \frac{1.7 \times 10^{-6}}{2.0 \times 10^{-6}} \\[10pt] &= 0.85 \quad \mathrm{[Ω]} \end{aligned} \](2) 1時間の発熱量:
\[ \begin{aligned} P &= I^2 \times R \\[10pt] &= 10^2 \times 0.85 \\[10pt] &= 85 \quad \mathrm{[W]} \\[10pt] H &= P \times t = 85 \times 3600 = 306,000 \quad \mathrm{[J]} \end{aligned} \](3) 銅の質量と温度上昇:
\[ \begin{aligned} \text{銅の密度:} &\quad 8900 \quad \mathrm{[kg/m^3]} \\[10pt] \text{銅の比熱:} &\quad 385 \quad \mathrm{[J/(kg \cdot K)]} \\[10pt] \text{導線体積:} &\quad V = A \times l = 2.0 \times 10^{-6} \times 100 = 2.0 \times 10^{-4} \quad \mathrm{[m^3]} \\[10pt] \text{導線質量:} &\quad m = 8900 \times 2.0 \times 10^{-4} = 1.78 \quad \mathrm{[kg]} \\[10pt] \text{温度上昇:} &\quad \Delta T = \frac{H}{m \times c} = \frac{306,000}{1.78 \times 385} ≈ 446 \quad \mathrm{[K]} \end{aligned} \]※実際は放熱により温度上昇は大幅に抑制される
実際の電気設備では、安全率を考慮して許容電流の70-80%程度で使用することが一般的です。また、電線を束ねて配線する場合や、高温環境で使用する場合は、許容電流をさらに低減する必要があります。これらの低減係数は、電気設備技術基準で詳細に規定されています。
- 導体断面積:太いほど抵抗が小さく許容電流大
- 導体材質:銅は銀に次ぐ良導体
- 周囲温度:高温環境では許容電流減少
- 冷却条件:空冷、強制冷却で許容電流向上
- 配線方法:密集配線では熱がこもりやすい
4. 熱エネルギーと電気エネルギーの関係
熱エネルギーと電気エネルギーの相互変換は、現代社会の基盤技術です。火力発電では熱エネルギーを電気エネルギーに変換し、電気ヒータでは電気エネルギーを熱エネルギーに変換します。また、熱電効果により、温度差から直接電気エネルギーを取り出すことも可能です。これらの変換過程を定量的に理解することは、エネルギー効率の向上と環境負荷軽減において重要です。
エネルギー変換の基本原理は、エネルギー保存の法則に基づいています。入力エネルギーは、有効出力エネルギーと損失エネルギーに分かれます。損失エネルギーの多くは熱として放散されるため、高効率化には損失の最小化が重要となります。特に電気機器では、電気損失(銅損、鉄損)、機械損失(摩擦損、風損)が主要な損失要因となります。
各種エネルギー変換装置の効率を比較してみましょう。火力発電所の総合効率は約40%、水力発電は90%以上、太陽電池は15-20%、燃料電池は40-60%、電気自動車のモータは90%以上となっています。これらの効率差は、変換メカニズムの違いと技術的制約によるものです。
石炭火力発電所において、石炭の燃焼熱量100MJから30MJの電気エネルギーを得た。残りは排熱として大気に放散された。
(1) 発電効率
(2) 排熱量
(3) 同じ電気エネルギーを電気ヒータで熱エネルギーに変換した場合の効率
解答:
(1) 発電効率:
\[ \begin{aligned} \eta_{発電} &= \frac{\text{電気エネルギー}}{\text{燃焼熱量}} \times 100 \\[10pt] &= \frac{30}{100} \times 100 \\[10pt] &= 30 \quad \mathrm{[\%]} \end{aligned} \](2) 排熱量:
\[ \begin{aligned} \text{排熱量} &= \text{燃焼熱量} - \text{電気エネルギー} \\[10pt] &= 100 - 30 \\[10pt] &= 70 \quad \mathrm{[MJ]} \end{aligned} \](3) 電気ヒータの効率:
\[ \begin{aligned} \eta_{ヒータ} &= \frac{\text{熱エネルギー}}{\text{電気エネルギー}} \times 100 \\[10pt] &= \frac{30}{30} \times 100 \\[10pt] &= 100 \quad \mathrm{[\%]} \end{aligned} \](電気ヒータは電気エネルギーをほぼ100%熱エネルギーに変換)
熱力学の第2法則により、熱エネルギーから電気エネルギーへの変換には理論的な限界があります。カルノー効率 \(\eta_c = 1 - T_L/T_H\)(\(T_H\):高温熱源温度、\(T_L\):低温熱源温度、単位はケルビン)が理論的な最大効率となります。実際の熱機関の効率は、この理論値を大幅に下回ります。
一方、電気エネルギーから熱エネルギーへの変換は、理論的に100%の効率が可能です。電気ヒータ、電気炉、電気溶接機などでは、ジュール熱を利用してほぼ完全な変換が実現されています。ただし、ヒートポンプ技術を用いれば、投入電気エネルギーの3-5倍の熱エネルギーを得ることも可能です。
電気エネルギーの貯蔵技術も重要な課題です。電気エネルギーは直接貯蔵が困難なため、他の形態のエネルギーに変換して貯蔵します。蓄電池では化学エネルギー、揚水発電では位置エネルギー、フライホイールでは運動エネルギー、圧縮空気貯蔵では圧力エネルギーとして貯蔵されます。
- 電気→熱:ほぼ100%効率、制御容易、瞬時応答
- 熱→電気:効率制限あり、大型設備、環境負荷
- 化学→電気:高エネルギー密度、携帯可能、充放電効率
- 光→電気:クリーン、無騒音、変換効率向上中
- 運動→電気:高効率、大容量、立地制約
コージェネレーション(熱電併給)システムは、廃熱の有効利用により総合効率を向上させる技術です。発電時に発生する排熱を暖房や給湯に利用することで、総合エネルギー効率を80%以上に向上できます。これは、エネルギーの多段階利用による効率向上の典型例です。
| 変換装置 | 入力エネルギー | 出力エネルギー | 効率[%] | 特徴 |
|---|---|---|---|---|
| 火力発電 | 化学エネルギー | 電気エネルギー | 35-45 | 大容量、安定供給 |
| 水力発電 | 位置エネルギー | 電気エネルギー | 85-95 | 高効率、長寿命 |
| 太陽電池 | 光エネルギー | 電気エネルギー | 15-25 | クリーン、分散型 |
| 電動機 | 電気エネルギー | 機械エネルギー | 85-95 | 制御性良好 |
| 電気ヒータ | 電気エネルギー | 熱エネルギー | 95-100 | 高効率、瞬時制御 |
| LED照明 | 電気エネルギー | 光エネルギー | 15-25 | 長寿命、低発熱 |
家庭用太陽光発電システム(3kW、効率20%)を設置した。晴天時の太陽光強度を1000W/m²とする。
(1) 必要な太陽電池パネル面積
(2) 1日8時間の日照で得られる電力量
(3) この電力をすべて電気ヒータで暖房に使用した場合の熱量
(4) 同じ熱量を石油ストーブ(効率80%)で得る場合の石油消費量
解答:
(1) パネル面積:
\[ \begin{aligned} \text{太陽光入力} &= \text{太陽光強度} \times \text{面積} \\[10pt] \text{電気出力} &= \text{太陽光入力} \times \text{効率} \\[10pt] 3000 &= 1000 \times S \times 0.20 \\[10pt] S &= \frac{3000}{1000 \times 0.20} = 15 \quad \mathrm{[m^2]} \end{aligned} \](2) 1日の電力量:
\[ \begin{aligned} W &= P \times t \\[10pt] &= 3 \times 8 \\[10pt] &= 24 \quad \mathrm{[kWh]} \end{aligned} \](3) 電気ヒータでの熱量:
\[ \begin{aligned} Q &= W \times \eta_{ヒータ} \\[10pt] &= 24 \times 1.0 \\[10pt] &= 24 \quad \mathrm{[kWh]} = 86.4 \quad \mathrm{[MJ]} \end{aligned} \](4) 石油消費量:
\[ \begin{aligned} \text{石油発熱量} &= \frac{Q}{\eta_{石油}} \\[10pt] &= \frac{86.4}{0.80} = 108 \quad \mathrm{[MJ]} \\[10pt] \text{石油消費量} &= \frac{108}{43} ≈ 2.5 \quad \mathrm{[L]} \\[10pt] &\text{(灯油の発熱量:43MJ/L)} \end{aligned} \]- ジュール熱:H = I²Rt、電流の2乗に比例
- 電力計算:P = VI = I²R = V²/R
- 電力量計算:W = Pt、単位換算(kWh、MJ)
- 許容電流:温度上昇を許容値以下に抑制
- 効率計算:η = P_out/P_in、損失最小化が重要
- エネルギー変換:各技術の特徴と効率差
- ジュール熱公式:3つの形(P=VI、I²R、V²/R)の使い分け
- 単位換算:kWh⇔MJ、カロリー変換(1cal=4.18J)
- 効率計算:入力・出力・損失の関係式
- 温度上昇:比熱、熱容量の概念理解
- 実用計算:電気料金、燃料消費量の算出
- 有効数字:計算精度と結果の表現方法
| 物理量 | 単位 | 換算関係 | 用途 |
|---|---|---|---|
| 電力 | W, kW, MW | 1kW = 1000W | 機器の定格表示 |
| 電力量 | Wh, kWh, MWh | 1kWh = 1000Wh | 電気料金計算 |
| エネルギー | J, kJ, MJ | 1kWh = 3.6MJ | 熱量計算 |
| 熱量 | cal, kcal | 1cal = 4.18J | 燃焼熱表示 |
第3節 電気抵抗の性質
1. 抵抗率と導電率
抵抗率(比抵抗)は、物質固有の電気的性質を表す重要な物理量です。同じ材料でも形状や寸法によって抵抗値は変化しますが、抵抗率は材料固有の値として一定です。抵抗率を理解することで、任意の形状・寸法の導体の抵抗値を計算でき、電気設備の設計や材料選択に活用できます。
抵抗率 \(\rho\)(ロー)は、単位長さ・単位断面積あたりの抵抗値として定義されます。長さ \(l\) [m]、断面積 \(A\) [m²]の導体の抵抗 \(R\) [Ω]は、抵抗率を用いて \(R = \rho l/A\) で表されます。この式から、導体を細く長くするほど抵抗が大きくなり、太く短くするほど抵抗が小さくなることが分かります。
R:抵抗[Ω]、ρ:抵抗率[Ω·m]、σ:導電率[S/m]、G:コンダクタンス[S]
l:長さ[m]、A:断面積[m²]
材料の導電性は、その結晶構造と電子の挙動によって決まります。金属では自由電子が多数存在し、低い抵抗率を示します。半導体では温度上昇により導電性が向上し、絶縁体では自由電子がほとんど存在せず、非常に高い抵抗率を示します。この分類は、材料の導電性の桁違いの差によって決まります。
アルミニウム線(抵抗率 2.8×10⁻⁸ Ω·m)を用いた送電線について、以下を求めよ。
線の直径:20mm、長さ:10km
(1) 断面積
(2) 送電線の抵抗
(3) 同じ抵抗の銅線(抵抗率 1.7×10⁻⁸ Ω·m)の直径
解答:
(1) 断面積:
\[ \begin{aligned} A &= \pi \times \left(\frac{d}{2}\right)^2 \\[10pt] &= \pi \times \left(\frac{20 \times 10^{-3}}{2}\right)^2 \\[10pt] &= \pi \times (10^{-2})^2 \\[10pt] &= \pi \times 10^{-4} ≈ 3.14 \times 10^{-4} \quad \mathrm{[m^2]} \end{aligned} \](2) 送電線抵抗:
\[ \begin{aligned} R &= \rho \frac{l}{A} \\[10pt] &= 2.8 \times 10^{-8} \times \frac{10 \times 10^3}{3.14 \times 10^{-4}} \\[10pt] &= 2.8 \times 10^{-8} \times \frac{10^4}{3.14 \times 10^{-4}} \\[10pt] &= 2.8 \times 10^{-8} \times 3.18 \times 10^7 \\[10pt] &≈ 0.89 \quad \mathrm{[Ω]} \end{aligned} \](3) 同じ抵抗の銅線直径:
\[ \begin{aligned} R_{銅} &= R_{Al} = 0.89 \quad \mathrm{[Ω]} \\[10pt] A_{銅} &= \rho_{銅} \frac{l}{R} \\[10pt] &= 1.7 \times 10^{-8} \times \frac{10^4}{0.89} \\[10pt] &≈ 1.91 \times 10^{-4} \quad \mathrm{[m^2]} \\[10pt] d_{銅} &= 2\sqrt{\frac{A_{銅}}{\pi}} \\[10pt] &= 2\sqrt{\frac{1.91 \times 10^{-4}}{\pi}} \\[10pt] &≈ 0.0156 \quad \mathrm{[m]} = 15.6 \quad \mathrm{[mm]} \end{aligned} \]抵抗率の実用的な応用として、電気探査法があります。地中に電流を流して抵抗率分布を測定することで、地質構造や地下水の分布を調べることができます。乾燥した土壌は高い抵抗率を示し、湿潤な土壌や金属鉱脈は低い抵抗率を示すため、この性質を利用して資源探査や地盤調査が行われています。
導電率の概念は、電解質溶液の分析にも重要です。イオン濃度が高い溶液ほど導電率が高くなるため、水質検査や化学分析で導電率測定が広く利用されています。純水の導電率は非常に低く(約5.5×10⁻⁶ S/m)、海水は約5 S/mと高い値を示します。
| 材料分類 | 材料名 | 抵抗率[Ω·m] | 用途例 |
|---|---|---|---|
| 金属導体 | 銀 | 1.6×10⁻⁸ | 高周波用導体 |
| 銅 | 1.7×10⁻⁸ | 電線、巻線 | |
| アルミニウム | 2.8×10⁻⁸ | 送電線、軽量化 | |
| 鉄 | 1.0×10⁻⁷ | 構造材、磁心 | |
| 半導体 | シリコン(純粋) | 10³ | 電子素子 |
| ゲルマニウム | 0.5 | ダイオード | |
| 絶縁体 | ガラス | 10¹² | 絶縁材料 |
| ゴム | 10¹³ | 電線被覆 | |
| 雲母 | 10¹⁵ | 高温絶縁 |
2. 抵抗の温度特性
ほとんどの材料において、抵抗値は温度によって変化します。この温度特性は、材料の種類によって大きく異なり、電気機器の設計や使用条件の設定において重要な考慮事項となります。金属では一般的に温度上昇とともに抵抗が増加し、半導体では逆に抵抗が減少します。この特性を理解することで、温度センサーの原理や電気機器の温度補償技術を理解できます。
金属の抵抗温度特性は、結晶格子の熱振動による電子散乱の増加により説明されます。温度が上昇すると原子の熱振動が激しくなり、自由電子の流れが妨げられるため抵抗が増加します。この現象は線形近似が可能で、温度係数という概念で定量化されます。
R_t:温度t℃での抵抗[Ω]、R_0:基準温度での抵抗[Ω]
α:温度係数[/℃]、t:温度[℃]
銅電線の抵抗が20℃で0.5Ωである。この電線の抵抗を以下の温度で求めよ。
銅の温度係数:α = 3.9×10⁻³ /℃(20℃基準)
(1) 0℃での抵抗
(2) 60℃での抵抗
(3) 抵抗が2倍になる温度
解答:
(1) 0℃での抵抗:
\[ \begin{aligned} R_0 &= R_{20}(1 + \alpha(0 - 20)) \\[10pt] R_0 &= 0.5 \times (1 + 3.9 \times 10^{-3} \times (-20)) \\[10pt] &= 0.5 \times (1 - 0.078) \\[10pt] &= 0.5 \times 0.922 \\[10pt] &= 0.461 \quad \mathrm{[Ω]} \end{aligned} \](2) 60℃での抵抗:
\[ \begin{aligned} R_{60} &= R_{20}(1 + \alpha(60 - 20)) \\[10pt] &= 0.5 \times (1 + 3.9 \times 10^{-3} \times 40) \\[10pt] &= 0.5 \times (1 + 0.156) \\[10pt] &= 0.5 \times 1.156 \\[10pt] &= 0.578 \quad \mathrm{[Ω]} \end{aligned} \](3) 抵抗が2倍になる温度:
\[ \begin{aligned} 2 \times 0.5 &= 0.5(1 + \alpha(t - 20)) \\[10pt] 2 &= 1 + 3.9 \times 10^{-3}(t - 20) \\[10pt] 1 &= 3.9 \times 10^{-3}(t - 20) \\[10pt] t - 20 &= \frac{1}{3.9 \times 10^{-3}} \\[10pt] t &= 20 + 256.4 = 276.4 \quad \mathrm{[℃]} \end{aligned} \]半導体の温度特性は金属とは大きく異なります。純粋な半導体では、温度上昇により価電子帯から伝導帯への電子の熱励起が増加し、キャリア(電子と正孔)の数が指数関数的に増加します。このため、半導体の抵抗は温度上昇とともに急激に減少します。この特性を利用したのがサーミスタ(熱敏抵抗器)です。
温度センサーとしての抵抗素子には、主に3つのタイプがあります。白金測温抵抗体(Pt100、Pt1000)は高精度で安定性に優れ、工業用途で広く使用されています。サーミスタは感度が高く小型化が容易で、家電製品の温度制御に使用されます。また、IC温度センサーは線形性に優れ、デジタル出力が可能です。
- 金属導体:正の温度係数、線形変化、高い安定性
- 半導体:負の温度係数、指数的変化、高い感度
- 絶縁体:負の温度係数、非線形変化、高温で導電性出現
- 超合金:温度係数極小、精密抵抗器に使用
3. 各種物質の抵抗値
材料の電気抵抗は、その原子構造と電子状態によって決まります。導体、半導体、絶縁体という分類は、電子のエネルギーバンド理論に基づいており、抵抗値は約20桁にわたって変化します。この巨大な範囲の違いにより、用途に応じた材料選択が可能になり、現代の電子技術が実現されています。
導体の中でも、銀は最も低い抵抗率を持ちますが、高価なため一般的には銅が使用されます。銅は優れた導電性と加工性、経済性を兼ね備えており、電線や巻線の標準材料となっています。アルミニウムは銅より導電性は劣りますが、軽量で安価なため、送電線や航空機用配線に使用されます。
半導体材料では、純粋なシリコンの抵抗率は約10³ Ω·mですが、微量の不純物を添加(ドーピング)することで、抵抗率を10⁻³ Ω·mから10⁶ Ω·mまで制御できます。この制御可能性が、トランジスタやダイオードなどの半導体素子の動作原理となっています。
同じ形状(長さ1m、断面積1mm²)の導体を銅、アルミニウム、鉄で作製した場合の抵抗値を比較せよ。
抵抗率:銅 1.7×10⁻⁸ Ω·m、アルミニウム 2.8×10⁻⁸ Ω·m、鉄 1.0×10⁻⁷ Ω·m
解答:
共通条件:
\[ \begin{aligned} l &= 1 \quad \mathrm{[m]} \\[10pt] A &= 1 \times 10^{-6} \quad \mathrm{[m^2]} \end{aligned} \]各材料の抵抗:
\[ \begin{aligned} R_{銅} &= 1.7 \times 10^{-8} \times \frac{1}{1 \times 10^{-6}} = 0.017 \quad \mathrm{[Ω]} \\[10pt] R_{Al} &= 2.8 \times 10^{-8} \times \frac{1}{1 \times 10^{-6}} = 0.028 \quad \mathrm{[Ω]} \\[10pt] R_{鉄} &= 1.0 \times 10^{-7} \times \frac{1}{1 \times 10^{-6}} = 0.10 \quad \mathrm{[Ω]} \end{aligned} \]銅を基準とした比:
\[ \begin{aligned} \text{Al/Cu} &= \frac{0.028}{0.017} ≈ 1.65 \text{倍} \\[10pt] \text{Fe/Cu} &= \frac{0.10}{0.017} ≈ 5.9 \text{倍} \end{aligned} \]絶縁材料の選択は、電気的特性だけでなく、機械的強度、耐熱性、耐薬品性も重要です。プラスチック系絶縁材料は軽量で加工しやすく、家電製品に広く使用されています。セラミック系材料は高温特性に優れ、電力機器の絶縁に使用されます。ガラス繊維強化プラスチック(FRP)は機械的強度と電気絶縁性を両立し、電気機器の構造材として重要です。
超導体は、特定の温度以下で電気抵抗が完全に零になる特殊な材料です。1911年にオランダの物理学者カメルリング・オンネスによって発見されました。従来の金属系超導体は極低温でのみ超導体となりましたが、1986年に発見された酸化物系高温超導体は液体窒素温度(-196℃)でも超導体となり、実用化への道を開きました。
| 材料分類 | 抵抗率範囲[Ω·m] | 温度特性 | 主な応用 |
|---|---|---|---|
| 超導体 | 0(転移温度以下) | 急激な転移 | 電力貯蔵、MRI、リニア |
| 良導体 | 10⁻⁸~10⁻⁶ | 正の温度係数 | 配線、送電線、接点 |
| 抵抗材料 | 10⁻⁷~10⁻⁴ | 小さい温度係数 | 抵抗器、ヒータ線 |
| 半導体 | 10⁻³~10⁶ | 負の温度係数 | ダイオード、トランジスタ |
| 絶縁体 | 10⁸~10¹⁶ | 負の温度係数 | 電線被覆、基板材料 |
4. 抵抗器の種類と用途
抵抗器は電子回路の基本素子として、電流制限、電圧分割、信号調整などの重要な役割を果たします。用途や要求仕様に応じて、様々な構造と材料の抵抗器が開発されています。適切な抵抗器の選択は、回路の性能と信頼性を左右する重要な設計要素です。抵抗値、許容電力、精度、温度特性、周波数特性などを総合的に考慮する必要があります。
固定抵抗器は、一定の抵抗値を持つ最も基本的な抵抗器です。炭素皮膜抵抗器は安価で汎用的ですが、精度と安定性は中程度です。金属皮膜抵抗器は高精度で温度特性に優れ、精密測定回路に使用されます。巻線抵抗器は大電力に対応でき、電力制御回路で重要な役割を果たします。
可変抵抗器(ボリューム、ポテンショメータ)は、抵抗値を連続的に変化させることができる抵抗器です。音量調節、明るさ調節、モータ速度制御など、様々な制御回路で使用されます。回転型と直線型があり、単連(1回路)から多連(複数回路同時制御)まで様々な形態があります。
12Vの電源に以下の抵抗器を接続した場合の消費電力を求め、許容電力と比較せよ。
(1) 100Ω、1/4W(0.25W)抵抗器
(2) 10Ω、2W抵抗器
(3) 1kΩ、1/8W(0.125W)抵抗器
解答:
(1) 100Ω抵抗器:
\[ \begin{aligned} P_1 &= \frac{V^2}{R} = \frac{12^2}{100} = \frac{144}{100} = 1.44 \quad \mathrm{[W]} \\[10pt] &\text{許容電力0.25Wを超過} → \text{使用不可} \end{aligned} \](2) 10Ω抵抗器:
\[ \begin{aligned} P_2 &= \frac{V^2}{R} = \frac{12^2}{10} = \frac{144}{10} = 14.4 \quad \mathrm{[W]} \\[10pt] &\text{許容電力2Wを大幅に超過} → \text{使用不可} \end{aligned} \](3) 1kΩ抵抗器:
\[ \begin{aligned} P_3 &= \frac{V^2}{R} = \frac{12^2}{1000} = \frac{144}{1000} = 0.144 \quad \mathrm{[W]} \\[10pt] &\text{許容電力0.125Wを超過} → \text{使用不可} \end{aligned} \]安全に使用するには、消費電力が許容電力の50-80%以下になるよう設計することが推奨される。
特殊抵抗器には、温度によって抵抗値が変化するサーミスタ、光によって抵抗値が変化するCdSセル(光導電素子)、電圧によって抵抗値が変化するバリスタなどがあります。これらの素子は、センサーや保護回路として重要な役割を果たしています。
表面実装型(SMD:Surface Mount Device)抵抗器は、現代の電子機器では主流となっています。小型化、自動実装対応、高密度実装が可能で、スマートフォンやコンピュータなどの小型電子機器に不可欠です。サイズは0201(0.6×0.3mm)から2512(6.4×3.2mm)まで標準化されています。
- 抵抗値:回路設計で決定される基本パラメータ
- 許容電力:消費電力の2-5倍の余裕を確保
- 精度:±1%、±5%など、回路要求に応じて選択
- 温度特性:動作温度範囲での抵抗変化
- 周波数特性:高周波回路では寄生成分を考慮
- 信頼性:故障率、寿命、耐環境性
| 種類 | 構造・材料 | 精度 | 電力範囲 | 主な用途 |
|---|---|---|---|---|
| 炭素皮膜 | 炭素膜をセラミック棒に蒸着 | ±5%~±20% | 1/8W~2W | 一般回路、汎用 |
| 金属皮膜 | 金属膜をセラミック棒に蒸着 | ±1%~±5% | 1/16W~1W | 精密回路、測定器 |
| 巻線型 | 抵抗線をボビンに巻く | ±1%~±5% | 1W~100W | 電力制御、負荷 |
| チップ型 | 厚膜または薄膜技術 | ±1%~±5% | 1/32W~1W | 高密度実装 |
| 可変型 | 炭素膜+摺動接点 | ±20%~±30% | 0.1W~2W | 調整、制御 |
第4節 電流の化学作用と電池
1. 電流の化学的作用
電流の化学的作用(電解作用)は、電流が電解質溶液や融解塩を通過する際に生じる化学反応です。この現象は1833年にマイケル・ファラデーによって定量的に解明され、現在では電解精錬、電気めっき、電池の動作原理など、工業的に極めて重要な技術となっています。電流の化学作用を理解することで、電池や電解プロセスの本質的な仕組みを把握できます。
電解現象の基本メカニズムは、イオンの移動と電極での酸化還元反応です。電解質溶液中では、正イオン(陽イオン)は陰極(カソード)に向かって移動し、負イオン(陰イオン)は陽極(アノード)に向かって移動します。電極表面では、電子の授受により化学反応が起こり、物質の分解や合成が進行します。
ファラデーの電解の法則は、電解により析出する物質の量と通電量の関係を定量的に表現します。第1法則では析出量が通電量に比例し、第2法則では同じ通電量でも物質の原子価によって析出量が異なることを示しています。これらの法則は、電気めっきの厚さ計算や電池容量の理論値算出に不可欠です。
m:析出量[g]、k:電気化学当量[g/C]、Q:電気量[C]
A:原子量[g/mol]、z:価数、F:ファラデー定数(96485 C/mol)
銅メッキを行うため、硫酸銅水溶液に2Aの電流を30分間流した。
銅の原子量:63.5、価数:2
(1) 通電電気量
(2) 理論析出量
(3) 電流効率80%の場合の実際の析出量
解答:
(1) 通電電気量:
\[ \begin{aligned} Q &= I \times t \\[10pt] &= 2 \times (30 \times 60) \\[10pt] &= 2 \times 1800 \\[10pt] &= 3600 \quad \mathrm{[C]} \end{aligned} \](2) 理論析出量:
\[ \begin{aligned} m &= \frac{A}{z \times F} \times Q \\[10pt] &= \frac{63.5}{2 \times 96485} \times 3600 \\[10pt] &= \frac{63.5}{192970} \times 3600 \\[10pt] &= 3.292 \times 10^{-4} \times 3600 \\[10pt] &≈ 1.185 \quad \mathrm{[g]} \end{aligned} \](3) 実際の析出量:
\[ \begin{aligned} m_{実際} &= m_{理論} \times \eta \\[10pt] &= 1.185 \times 0.80 \\[10pt] &= 0.948 \quad \mathrm{[g]} \end{aligned} \]電解作用の工業応用は多岐にわたります。電解精錬では、粗銅から純度99.99%以上の電気銅を製造します。電気めっきでは、装飾目的や防食目的で様々な金属を薄く析出させます。電解加工では、金属の精密切削が可能です。また、水の電解により水素と酸素を製造することは、クリーンエネルギーの観点から注目されています。
電解効率は実用的に重要な概念です。理論値と実際の析出量の比として定義され、副反応の発生、電極の過電圧、イオンの拡散律速などにより100%を下回ります。工業プロセスでは、電解効率の向上が経済性と環境負荷軽減の両面で重要な課題となっています。
- 電解精錬:銅、亜鉛、アルミニウムなどの高純度金属製造
- 電気めっき:防食、装飾、電気接点の改良
- 電解加工:精密部品の加工、バリ取り
- 水電解:水素製造、酸素製造
- 電解合成:塩素、水酸化ナトリウムの工業製造
2. 電池の原理と分類
電池は化学エネルギーを電気エネルギーに変換する装置で、現代社会のモバイル機器や電気自動車の普及に不可欠な技術です。電池の動作原理は、異なる2つの電極間で生じる酸化還元反応の電位差を利用したものです。1800年にアレッサンドロ・ボルタが発明したボルタ電池が現代電池技術の出発点となっています。
電池の基本構造は、正極(陽極)、負極(陰極)、電解質から構成されます。負極では酸化反応により電子を放出し、正極では還元反応により電子を受け取ります。電解質はイオンの移動経路となり、外部回路で電子の流れ(電流)が生じます。この化学反応により生じる電位差が電池の起電力となります。
電池は大きく一次電池(使い捨て)と二次電池(充電式)に分類されます。一次電池は化学反応が不可逆で、放電のみ可能です。マンガン乾電池、アルカリ電池、リチウム一次電池などがあります。二次電池は充放電反応が可逆で、繰り返し使用可能です。鉛蓄電池、ニッケル水素電池、リチウムイオン電池などが代表例です。
V:端子電圧[V]、E:起電力[V]、I:電流[A]、r:内部抵抗[Ω]
C:容量[Ah]、W:エネルギー[Wh]、η:効率[%]
起電力12V、内部抵抗0.1Ωの鉛蓄電池に、抵抗値2.9Ωの負荷を接続した。
(1) 負荷電流
(2) 端子電圧
(3) 負荷での消費電力
(4) 内部抵抗での損失電力
解答:
(1) 負荷電流:
\[ \begin{aligned} I &= \frac{E}{r + R_L} \\[10pt] &= \frac{12}{0.1 + 2.9} \\[10pt] &= \frac{12}{3.0} \\[10pt] &= 4 \quad \mathrm{[A]} \end{aligned} \](2) 端子電圧:
\[ \begin{aligned} V &= E - I \times r \\[10pt] &= 12 - 4 \times 0.1 \\[10pt] &= 12 - 0.4 \\[10pt] &= 11.6 \quad \mathrm{[V]} \end{aligned} \](3) 負荷消費電力:
\[ \begin{aligned} P_L &= I^2 \times R_L \\[10pt] &= 4^2 \times 2.9 \\[10pt] &= 16 \times 2.9 \\[10pt] &= 46.4 \quad \mathrm{[W]} \end{aligned} \](4) 内部損失電力:
\[ \begin{aligned} P_r &= I^2 \times r \\[10pt] &= 4^2 \times 0.1 \\[10pt] &= 16 \times 0.1 \\[10pt] &= 1.6 \quad \mathrm{[W]} \end{aligned} \]現代の電池技術で最も注目されているのはリチウムイオン電池です。1991年にソニーが実用化して以来、携帯電話、ノートパソコン、電気自動車まで幅広く使用されています。高いエネルギー密度、長寿命、メモリー効果がないなどの優れた特性を持ちますが、安全性確保のための保護回路が必要です。
電池の性能指標として、エネルギー密度(Wh/kg)、出力密度(W/kg)、サイクル寿命(充放電回数)、安全性、コストが重要です。用途により重視される特性が異なり、電気自動車用ではエネルギー密度と安全性、電力貯蔵用では寿命とコスト、携帯機器用では小型軽量化が優先されます。
次世代電池として、全固体電池、金属空気電池、燃料電池などの研究が活発です。全固体電池は電解質を固体化することで安全性と性能の向上を図り、金属空気電池は理論的に非常に高いエネルギー密度を持ちます。燃料電池は水素と酸素の反応により発電し、排出物が水のみというクリーンな特性を持っています。
| 電池種類 | 公称電圧[V] | エネルギー密度[Wh/kg] | サイクル寿命 | 主な用途 |
|---|---|---|---|---|
| マンガン乾電池 | 1.5 | 80-120 | -(一次電池) | 時計、リモコン |
| アルカリ電池 | 1.5 | 120-160 | -(一次電池) | 懐中電灯、玩具 |
| 鉛蓄電池 | 2.0 | 30-50 | 500-1000 | 自動車、UPS |
| ニッケル水素 | 1.2 | 60-90 | 500-1000 | ハイブリッド車 |
| リチウムイオン | 3.6-3.7 | 120-250 | 1000-3000 | スマホ、EV |
| 燃料電池 | 0.7-1.0 | 500-1000 | 5000-10000 | FCV、定置用 |
- 電圧・容量:回路設計に必要な電気的仕様
- エネルギー密度:軽量化・小型化の要求
- 出力密度:瞬間的な大電流供給能力
- 寿命特性:充放電サイクル数、保存特性
- 安全性:過充電、過放電、短絡に対する安全性
- 環境性:動作温度範囲、廃棄・リサイクル
- 経済性:初期コスト、ランニングコスト
- 抵抗率と導電率:R = ρl/A、材料固有の電気的性質
- 温度特性:金属は正、半導体は負の温度係数
- 抵抗器:許容電力、精度、温度特性が重要
- 電解作用:ファラデーの法則、工業応用
- 電池の原理:化学エネルギー→電気エネルギー変換
- 電池特性:起電力、内部抵抗、容量、寿命
- 抵抗率計算:R = ρl/A の公式適用
- 温度補正:R_t = R_0(1 + αt) の使い方
- 電力計算:P = V²/R = I²R、許容電力との比較
- 電解計算:ファラデー定数96485 C/mol の活用
- 電池回路:内部抵抗を含む回路計算
- 単位換算:Ah⇔C、Wh⇔J の関係