【第三種電気主任技術者試験】送電分野の完全ガイド - 架空送電線路・送電損失・中性点接地方式
目次
1. イントロダクション
送電とは、発電所で発電された電力を変電所や配電設備を経由して、需要地まで送り届けるための技術です。現代の電力系統において、送電技術は電力の安定供給を支える重要な役割を担っています。


送電の重要性
送電技術は、発電所から離れた場所に電力を効率よく届けるために不可欠です。日本の電力系統では、主に高電圧の交流送電が採用されており、電力損失を低減するために様々な技術が用いられています。
日常生活や産業での応用例
私たちの日常生活や産業活動は、送電技術によって支えられています:
- 家庭や事業所へ安定した電力供給を実現
- 遠隔地の大規模発電所(火力、水力、原子力など)からの電力輸送
- 再生可能エネルギー(太陽光、風力など)の系統連系と電力輸送
- 電力会社間の電力融通による広域的な電力安定供給
第三種電気主任技術者試験における位置づけ
送電分野は、第三種電気主任技術者試験の「電力科目」において重要な出題範囲となっています。特に以下の項目が頻出です:
- 送電線路の構成と種類
- 送電線路の電気的特性(電力損失、電圧降下など)
- 中性点接地方式
- 送電線路の保護方式
- 高電圧工学の基礎知識
学習の進め方
送電技術を効果的に学習するためには、以下のステップで進めることをお勧めします:
- 送電線路の基本構成と設備について理解する
- 送電方式の種類と特徴を学ぶ
- 送電線路の電気的特性と関連する計算方法を習得する
- 送電線路の運用と保護について理解する
- 高電圧工学の基礎概念を学ぶ
- 演習問題を解いて理解度を確認する
2. 基礎概念
2.1 送電線路の構成と設備
送電線路は、発電所から変電所、あるいは変電所から変電所へ電力を送るための設備です。送電線路は主に架空送電線路と地中送電線路に分類されます。第三種電気主任技術者試験では、送電線路の構成と設備に関する問題が頻出するため、各構成要素の特徴と役割を正確に理解することが重要です。
架空送電線路
架空送電線路は、鉄塔や電柱などの支持物を用いて、空中に送電線を張り巡らせる方式です。日本の送電線路の大部分はこの架空送電線路で構成されており、特に郊外や山間部で多く採用されています。
架空送電線路の主な構成要素には以下のものがあります:
- 導体(電線):電流を流すための金属線。電圧階級や必要な送電容量によって種類と太さが選定されます。
- アルミ導体鋼心より線(ACSR: Aluminum Conductor Steel Reinforced):中心に鋼線を配置し、その周りにアルミ導体を撚り合わせた構造。機械的強度と導電性のバランスが良く、最も一般的に使用されています。
- アルミ合金導体鋼心より線(TACSR: Thermal-resistant Aluminum alloy Conductor Steel Reinforced):耐熱アルミ合金を使用し、高温でも機械的強度を維持できるため、大容量送電に適しています。
- ギャップ形アルミ導体鋼心より線(GACSR: Gap-type Aluminum Conductor Steel Reinforced):鋼心とアルミ導体の間に隙間があり、熱膨張差による弛度増加を抑制できます。
- 低弛度電線(TACIR/ZTACIR):インバー合金を使用し、熱膨張係数が小さいため、温度上昇による弛度増加が少なく、鉄塔間隔を広げることができます。
 イメージ図:アルミ合金導体鋼心より線
イメージ図:アルミ合金導体鋼心より線 - がいし(碍子):導体を支持物に絶縁して取り付けるための部品。送電電圧に応じて必要連数が決定されます。
- 懸垂がいし:鉄塔上部から垂直に吊り下げる形式で使用され、複数のがいしを連結して使用します。高圧・特別高圧の送電線に多く使用されます。
- 長幹がいし:水平方向に取り付けられ、主に電柱や小型支持物に使用されます。
- ポリマーがいし:シリコーンゴムなどの高分子材料を使用したがいしで、軽量で汚損に強いという特徴があります。
がいしの選定では、送電電圧に応じた絶縁耐力、機械的強度、汚損耐電圧などを考慮します。電圧が高くなるほど、がいしの連数を増やして絶縁距離を確保する必要があります。
- 支持物:鉄塔や電柱などの構造物。送電電圧や線路条件によって様々な形状があります。
- 鉄塔の種類:
- 懸垂型(I型)鉄塔:直線部に使用される最も基本的な形状の鉄塔
- 耐張型(V型)鉄塔:線路の方向変化点や引留め箇所に使用される鉄塔
- 分岐型(Y型)鉄塔:送電線路の分岐点に使用される鉄塔
- 終端型鉄塔:送電線路の終端に使用される鉄塔
- 鉄塔の設計要素:風圧荷重、着氷荷重、短絡時の電磁力、安全率などを考慮して設計されます。
鉄塔の高さや形状は、送電電圧、送電容量、鉄塔間隔(径間)、地形条件などによって決定されます。特別高圧送電線では、電線間および電線と地面との離隔距離を確保するため、高さが数十メートルに達する大型鉄塔が使用されます。
- 鉄塔の種類:
- 架空地線(OHGW: Overhead Ground Wire):雷撃から送電線を保護するために設置される接地線。
- 一般的な架空地線:鋼より線または亜鉛めっき鋼より線が使用されます。
- OPGW(Optical fiber composite Ground Wire):架空地線の中に光ファイバーを内蔵したもので、雷保護機能と通信機能を兼ね備えています。現代の送電線路では広く採用されており、電力系統の監視・制御データや通信データの伝送に利用されます。
架空地線の保護角(送電線と架空地線を結ぶ線と鉛直線のなす角)は、一般的に30度以下に設定され、この範囲内に送電線が収まるように配置されます。
- 腕金:支持物から張り出して、がいしを取り付けるための部材。
- 電線の配置パターン(水平配列、三角配列、逆三角配列など)に応じた形状があります。
- 送電容量や電圧によって必要な電線間隔を確保できる長さに設計されます。
- アーマロッド:がいし近傍の電線に取り付けられる保護金具で、電線のコロナ放電による損傷や、振動による疲労損傷を防止します。
- スペーサ:複導体(1相あたり複数の導体を使用)の場合に、導体間隔を一定に保つための金具です。
- ダンパ:風による電線の振動(ギャロッピング、バイブレーションなど)を抑制するための装置です。

架空送電線路の特徴
・建設コストが比較的低い(地中送電線路の1/3〜1/5程度)
・保守・点検が容易で、故障時の修復も比較的短時間で可能
・自然環境(雷、風、雪、塩害など)の影響を受けやすい
・景観への影響がある
・広い用地と鉄塔間の空間が必要
・電圧階級によって必要な絶縁離隔距離が異なる(66kV:約1m、154kV:約2m、275kV:約3m、500kV:約5m)
・コロナ放電による電力損失やノイズが発生することがある(特に高電圧送電線)
絶縁離隔距離の計算例(第三種電気主任技術者試験対策)
送電電圧が77kVの架空送電線路における最小絶縁離隔距離を簡易的に計算する。
解答:
架空送電線路の相間および相-大地間の絶縁離隔距離は、一般的に次の簡易式で概算できます:
\[d ≈ \frac{U}{150} + 0.5 \, \text{[m]}\]
ここで、\(U\)は送電線路の最高電圧[kV]です。
77kVの場合:
\[d ≈ \frac{77}{150} + 0.5 ≈ 0.51 + 0.5 = 1.01 \, \text{[m]}\]
したがって、最小絶縁離隔距離は約1.01mとなります。実際の設計では安全率を考慮して、これより大きな離隔距離を確保します。
地中送電線路
地中送電線路は、ケーブルを地中に埋設して電力を送る方式です。主に都市部や景観への配慮が必要な地域、あるいは空港周辺などの上空制限がある地域で採用されています。また、海峡や河川を横断する場合には海底・河底ケーブルとして使用されます。

地中送電線路の主な構成要素には以下のものがあります:
- ケーブル:地中送電に使用される専用の電力ケーブル。
- CVケーブル(Cross-linked polyethylene insulated Vinyl sheathed cable):架橋ポリエチレン絶縁ビニルシースケーブル。現在最も広く使用されている絶縁材料で、耐熱性、耐久性に優れています。
- OFケーブル(Oil-Filled cable):油浸絶縁紙ケーブル。絶縁油を循環させて冷却する方式で、主に大容量・高電圧送電に使用されてきましたが、現在は環境への配慮からCVケーブルへの置き換えが進んでいます。
- POFケーブル(Pipe-type Oil-Filled cable):鋼管に収納した油浸絶縁紙ケーブル。高電圧・大容量送電に適していますが、設置コストが高く、近年は使用が減少しています。
- ガス絶縁ケーブル(GIL: Gas Insulated transmission Line):SF6ガス(六フッ化硫黄)を絶縁媒体とした金属管内に導体を配置する方式。超高圧大容量送電に適しています。
ケーブルの構造は、内側から導体、絶縁体、遮蔽層、外装(防水層)という多層構造になっています。特に高電圧ケーブルでは、絶縁体内の電界分布を均一化するために導体表面に半導電層が設けられています。
- 布設方式:地中ケーブルの設置方法には以下の種類があります。
- 管路式:コンクリート管や塩化ビニル管内にケーブルを引き込む方式。最も一般的な布設方法で、ケーブルの交換や増設が比較的容易です。
- 直接埋設式:ケーブルを直接地中に埋設する方式。コスト面で有利ですが、ケーブルの修理や交換時に再掘削が必要です。
- 暗渠式(トラフ式):コンクリート製の箱形暗渠内にケーブルを敷設する方式。複数のケーブルを整然と配置できます。
- 洞道式:人が入れる大きさのトンネル(共同溝など)内にケーブルを敷設する方式。都市部の主要幹線で採用され、保守点検が容易ですが、建設コストが高いです。
- マンホール:ケーブルの接続や点検のために設置される空間。
- 一般的に50〜100m間隔で設置され、ケーブルの引き込み、接続作業、点検などに使用されます。
- 人が入って作業できる広さが確保され、換気、排水、照明などの設備を備えています。
- 接続部(ジョイント):ケーブル同士を接続するための部分。
- 直線接続部(ストレートジョイント)、分岐接続部(ブランチジョイント)などがあります。
- 接続部は電気的・機械的に弱点となりやすいため、高度な接続技術と品質管理が必要です。
- 終端部(ターミネーション):地中ケーブルと架空線を接続するための部分。
- 地中ケーブルと架空線の接続部分では、電界集中を緩和する特殊な構造が採用されています。
- 屋外用と屋内用(GIS接続用など)があります。
- 冷却設備:大容量送電の場合、ケーブルの許容電流を増加させるために冷却設備が設置されることがあります。
- 強制冷却方式(油循環や水循環など)により、ケーブル温度を下げて送電容量を増加させます。
地中送電線路の特徴
・自然環境(雷、風、雪、塩害など)の影響を受けにくい
・景観への影響が少なく、都市部での送電に適している
・建設コストが高い(架空送電線路の3〜5倍)
・静電容量が大きく、充電電流が増加する(長距離送電では補償設備が必要)
・故障時の探査や修理が難しく、復旧に時間がかかる
・ケーブルの冷却が重要で、許容電流は熱的制約を受ける
・電磁界が地表で遮蔽されるため、電磁環境への影響が小さい
・ケーブルの絶縁設計が重要(特に高電圧送電の場合)
地中ケーブルの充電電流の計算
地中ケーブルの静電容量は架空線よりも大きく、充電電流が問題となります。充電電流は以下の式で計算できます:
\[I_c = 2\pi f C V \,\, [A/km/相]\]
ここで、
\(I_c\) = 充電電流 [A/km/相]
\(f\) = 周波数 [Hz]
\(C\) = 静電容量 [F/km/相]
\(V\) = 相電圧 [V]
例えば、66kVのCVケーブル(静電容量:0.25μF/km/相)の場合、充電電流は:
\[I_c = 2\pi \times 60 \times 0.25 \times 10^{-6} \times \frac{66 \times 10^3}{\sqrt{3}} \approx 3.0 \,\, [A/km/相]\]
架空線と地中ケーブルの比較(試験対策)
架空送電線路と地中送電線路の違いについて、以下の項目で比較してください。
(1) 建設コスト (2) 送電可能距離 (3) 許容電流 (4) 故障率と復旧時間
解答:
(1) 建設コスト:地中送電線路は架空送電線路に比べて3〜5倍高い。これは、掘削工事、管路設置、マンホール設置などの土木工事費用に加え、ケーブル自体の価格も高いためである。
(2) 送電可能距離:地中ケーブルは静電容量が大きく充電電流が増加するため、補償設備なしでの送電可能距離は架空線に比べて短い。一般的に、高圧CVケーブルでは10〜20km程度が経済的な限界とされている。
(3) 許容電流:同じ導体断面積の場合、地中ケーブルは熱放散が困難なため、架空線よりも許容電流が小さい。ただし、複数回線の敷設が容易なため、総送電容量は確保しやすい。
(4) 故障率と復旧時間:地中ケーブルは外部環境の影響を受けにくいため故障率は架空線よりも低いが、一旦故障した場合の原因特定や修復に要する時間は長く、数日から数週間かかることもある。一方、架空線は故障率が高いものの、目視点検が可能で復旧も比較的短時間(数時間〜数日)で可能なことが多い。
2.2 送電方式とその特徴
交流送電と直流送電の比較
送電方式は大きく交流送電と直流送電(HVDC: High Voltage Direct Current)に分けられます。
| 項目 | 交流送電 | 直流送電(HVDC) |
|---|---|---|
| 主な特徴 | ・変圧器で電圧変換が容易 ・多数地点への送電が容易 |
・長距離送電に適する ・異周波数系統の連系が可能 |
| 損失 | ・静電容量による充電電流損 ・表皮効果による損失 |
・変換所での損失 ・線路損失は少ない |
| 設備 | ・変圧器による電圧変換 ・CB(遮断器)などの開閉機器 |
・変換所(サイリスタなど) ・フィルタ設備 |
| 適用例 | ・一般的な電力系統 ・近・中距離送電 |
・長距離送電(北海道-本州間連系など) ・海底ケーブル ・異周波数連系(東西日本間) |
直流送電の実例
日本国内では、以下のような直流送電設備があります:
- 北海道・本州間電力連系設備(±250kV、600MW)
- 阿南紀北直流連系設備(±500kV、1,400MW)- 東西日本の周波数変換設備
- 四国・本州間連系設備(±500kV、1,400MW)
単回線送電と複回線送電
送電線路の回線数による分類として、単回線送電と複回線送電があります。
| 項目 | 単回線送電 | 複回線送電 |
|---|---|---|
| 構成 | 1つの回線(三相線)のみで構成 | 2つ以上の回線を並行して設置 |
| 信頼性 | 1回線故障で全停電 | 1回線故障でも他回線で送電可能 |
| 送電容量 | 単一回線の容量に制限 | 複数回線の合計容量まで送電可能 |
| 建設コスト | 比較的低い | 高い(鉄塔が大型化) |
| 用地 | 比較的狭い | 広い(ただし単回線を2ルート確保するより狭い) |
複回線送電の利点
複回線送電は、供給信頼度の向上、送電容量の増加、将来の容量拡張への対応などの利点があります。特に重要な送電線路では、信頼性向上のために複回線方式が採用されています。
3. 数式と理論
3.1 送電線路の電気的特性
送電線路は電気的に分布定数回路として扱われ、以下の4つの基本的なパラメータで特性が表されます:
- 直列抵抗 \(R\):導体の抵抗による電力損失を引き起こす要素
- 直列インダクタンス \(L\):導体に電流が流れるとき、自己および相互インダクタンスにより生じる要素
- 並列コンダクタンス \(G\):絶縁体を通じての漏れ電流を表す要素
- 並列キャパシタンス \(C\):導体間および導体と大地間の静電容量を表す要素
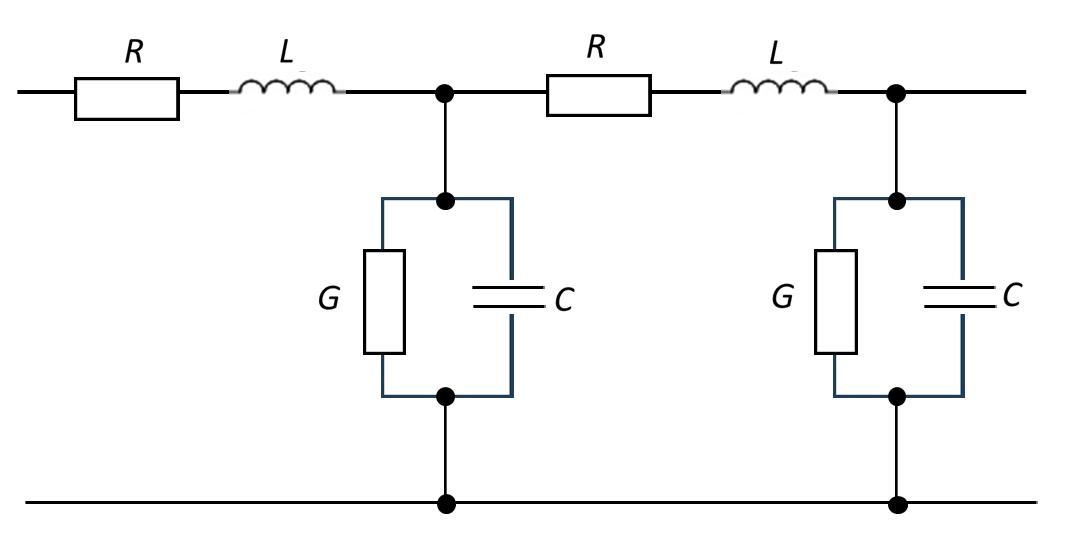
これらのパラメータは単位長さあたりの値として表され、以下のように線路定数と呼ばれています:
\(r\) = 単位長さあたりの抵抗 [Ω/km]
\(l\) = 単位長さあたりのインダクタンス [H/km]
\(g\) = 単位長さあたりのコンダクタンス [S/km]
\(c\) = 単位長さあたりのキャパシタンス [F/km]
送電線路の全長を \(l\) [km] とすると、全体のパラメータは次のようになります:
\[R = r \times l \,\, [\Omega]\]
\[L = l \times l \,\, [H]\]
\[G = g \times l \,\, [S]\]
\[C = c \times l \,\, [F]\]
一般的に送電線路の解析では、\(G\) は非常に小さいため無視されることが多いです。
3.2 送電損失と電圧降下
送電損失(電力損失)
送電線路における電力損失は主に導体の抵抗によるジュール熱として発生します。三相送電線路の電力損失は以下の式で計算できます:
\[P_{loss} = 3 I^2 R \,\, [W]\]
ここで、
- \(P_{loss}\) = 電力損失 [W]
- \(I\) = 線路電流 [A]
- \(R\) = 線路一相あたりの抵抗 [Ω]
送電電力 \(P\) と受電端電圧 \(V\)、力率 \(\cos \phi\) を用いると、電力損失は次のように表すこともできます:
\[P_{loss} = \frac{P^2 R}{V^2 \cos^2 \phi} \,\, [W]\]
例題:送電損失の計算
抵抗 \(R = 5 \,\Omega\) の送電線路で、線路電流 \(I = 200 \,A\) が流れている場合の三相送電線路の電力損失を求めなさい。
解答:
三相送電線路の電力損失は次の式で計算できます:
\[P_{loss} = 3 I^2 R\]
各値を代入して:
\begin{align*} P_{loss} &= 3 \times (200 \,A)^2 \times 5 \,\Omega \\ &= 3 \times 40,000 \times 5 \\ &= 600,000 \,W \\ &= 600 \,kW \end{align*}
したがって、電力損失は 600 kW となります。
電圧降下
送電線路の電圧降下は、抵抗とインダクタンスによって生じます。短距離送電線路(100km以下)の場合、送電線路を集中定数回路として扱い、電圧降下は以下の式で近似できます:
\[\Delta V \approx IR\cos\phi + IX\sin\phi \,\, [V]\]
ここで、
- \(\Delta V\) = 電圧降下 [V]
- \(I\) = 線路電流 [A]
- \(R\) = 線路抵抗 [Ω]
- \(X\) = 線路リアクタンス [Ω]
- \(\cos\phi\) = 力率
- \(\sin\phi\) = \(\sqrt{1-\cos^2\phi}\)
送電電力 \(P\) と受電端電圧 \(V\) を用いると、電圧降下率は次のように表されます:
\[\varepsilon = \frac{\Delta V}{V} \times 100 \,\, [\%]\]
電圧降下の低減方法
・送電電圧を上げる(送電電圧を2倍にすると電流は1/2になり、電圧降下は1/2に、電力損失は1/4になる)
・導体断面積を大きくする(抵抗を下げる)
・力率を改善する(進相コンデンサの設置など)
・直列コンデンサを設置する(線路リアクタンスを相殺)
例題:電圧降下の計算
抵抗 \(R = 2 \,\Omega\)、リアクタンス \(X = 5 \,\Omega\) の送電線路で、電流 \(I = 100 \,A\)、力率 \(\cos\phi = 0.8\)(遅れ)の負荷に送電している場合の電圧降下を求めなさい。
解答:
電圧降下は次の式で計算できます:
\[\Delta V = IR\cos\phi + IX\sin\phi\]
\(\sin\phi = \sqrt{1-\cos^2\phi} = \sqrt{1-0.8^2} = \sqrt{1-0.64} = \sqrt{0.36} = 0.6\)
各値を代入して:
\begin{align*} \Delta V &= 100 \,A \times 2 \,\Omega \times 0.8 + 100 \,A \times 5 \,\Omega \times 0.6 \\ &= 160 + 300 \\ &= 460 \,V \end{align*}
したがって、電圧降下は 460 V となります。
3.3 力率の影響と改善
力率は、皮相電力に対する有効電力の比率で、電力システムの効率を表す重要な指標です。第三種電気主任技術者試験では、力率に関する計算問題が頻出するため、計算方法の理解と演習が重要です。力率は以下の式で表されます:
\[\cos\phi = \frac{P}{S} = \frac{P}{\sqrt{P^2+Q^2}}\]
ここで、
- \(\cos\phi\) = 力率
- \(P\) = 有効電力 [W]
- \(S\) = 皮相電力 [VA]
- \(Q\) = 無効電力 [var]
- \(\phi\) = 電圧と電流の位相差 [rad]
力率に関する重要な関係式
電力の三角形から導かれる重要な関係式:
・\(S^2 = P^2 + Q^2\)(皮相電力、有効電力、無効電力の関係)
・\(P = S \cos\phi\)(有効電力)
・\(Q = S \sin\phi\)(無効電力)
・\(\tan\phi = \frac{Q}{P}\)(力率角の正接)
これらの関係式を理解することで、力率計算を効率的に行うことができます。
力率の送電線路への影響
力率が低い(特に遅れ力率の場合)と、送電線路に以下のような悪影響が生じます:
- 電流増加:同じ有効電力を送るために必要な電流が増加します。力率0.7では、力率1.0の場合に比べて約1.43倍の電流が必要になります。
- 電力損失増加:電力損失(\(P_{loss} = I^2R\))は電流の2乗に比例するため、力率が低いと損失が大幅に増加します。例えば、力率0.7では力率1.0の場合に比べて約2倍(1.43の2乗)の電力損失が生じます。
- 電圧降下増加:\(\Delta V = IR\cos\phi + IX\sin\phi\) の式からわかるように、力率が低いと電圧降下が増加します。
- 設備利用率低下:変圧器や送電線などの設備は皮相電力(VA)で容量が決まるため、力率が低いと設備の利用効率が悪くなります。
- 電圧安定性低下:無効電力の増加は系統の電圧安定性を悪化させ、電圧崩壊のリスクを高めます。
力率と必要な電流の関係は以下の式で表されます:
\[I = \frac{P}{V\cos\phi} \,\, [A]\]
この式から、同じ有効電力 \(P\) を送電する場合、力率 \(\cos\phi\) が低いほど必要な電流 \(I\) は大きくなることがわかります。
電流増加と電力損失の計算例
力率 \(\cos\phi = 0.8\)(遅れ)の負荷に対し、力率を1.0まで改善した場合の電流減少率と電力損失減少率を計算してみましょう。
解答:
改善前の電流を \(I_1\)、改善後の電流を \(I_2\) とすると:
\begin{align*} \frac{I_2}{I_1} &= \frac{P/(V\cos\phi_2)}{P/(V\cos\phi_1)} \\ &= \frac{\cos\phi_1}{\cos\phi_2} \\ &= \frac{0.8}{1.0} \\ &= 0.8 \end{align*}
つまり、電流は改善前の80%になり、電流減少率は20%です。
電力損失は電流の2乗に比例するため、電力損失の比率は:
\begin{align*} \frac{P_{loss,2}}{P_{loss,1}} &= \left(\frac{I_2}{I_1}\right)^2 \\ &= (0.8)^2 \\ &= 0.64 \end{align*}
つまり、電力損失は改善前の64%になり、電力損失減少率は36%です。
このように、力率改善によって電流と電力損失を大幅に削減できることがわかります。
力率改善の方法
力率を改善するには、遅れ無効電力を減少させる(または進み無効電力を供給する)必要があります。主な改善方法は以下の通りです:
- 進相コンデンサの設置:
- 最も一般的な力率改善方法で、負荷と並列に接続します。
- コンデンサは進み無効電力を発生させ、負荷の遅れ無効電力を相殺します。
- 設置コストが比較的低く、保守が容易です。
- 高調波がある環境では、直列リアクトルを設置して共振を防止する必要があります。
- 設置方式には、集中補償方式(変電所など一箇所に大容量設置)と分散補償方式(各負荷近くに小容量を分散設置)があります。
- 同期調相機の設置:
- 同期電動機を無負荷で運転し、励磁を調整することで無効電力を供給または吸収します。
- 連続的な無効電力制御が可能で、系統の安定化にも寄与します。
- 過励磁で進み無効電力(コンデンサと同様)を供給し、不足励磁で遅れ無効電力を吸収します。
- 設備コストが高く、保守が必要なため、大規模システムに適しています。
- 静止型無効電力補償装置(SVC: Static Var Compensator)の設置:
- サイリスタ制御のリアクトル(TCR)とスイッチングコンデンサ(TSC)を組み合わせた装置です。
- 高速かつ連続的な無効電力制御が可能で、電圧変動が大きい系統に適しています。
- アーク炉など、急激に負荷が変動する設備に有効です。
- 設備コストが高いですが、回転部分がないため保守は比較的容易です。
- 無効電力制御付き新型パワーエレクトロニクス機器:
- STATCOM(Static Synchronous Compensator):SVCよりも応答が速く、小型の無効電力補償装置
- アクティブフィルタ:高調波抑制と力率改善を同時に行う装置
- UPFC(Unified Power Flow Controller):送電線の有効・無効電力制御や電力潮流制御を行う装置
進相コンデンサ容量の計算
進相コンデンサによる力率改善の場合、必要なコンデンサ容量は以下の式で計算できます:
\[Q_C = P(\tan\phi_1 - \tan\phi_2) \,\, [var]\]
ここで、
- \(Q_C\) = 必要なコンデンサ容量 [var]
- \(P\) = 有効電力 [W]
- \(\phi_1\) = 改善前の力率角
- \(\phi_2\) = 改善後の力率角
また、\(\tan\phi\) は力率から以下の式で求めることができます:
\[\tan\phi = \frac{\sin\phi}{\cos\phi} = \frac{\sqrt{1-\cos^2\phi}}{\cos\phi}\]
例題:力率改善の計算
有効電力 \(P = 100 \,kW\)、力率 \(\cos\phi = 0.7\)(遅れ)の負荷がある。この力率を0.95(遅れ)まで改善するために必要な進相コンデンサの容量を求めなさい。
解答:
力率から \(\sin\phi\) を計算し、有効電力 \(P\) と力率 \(\cos\phi\)、および \(\sin\phi\) を用いて必要な容量を計算します。
改善前: \(\cos\phi_1 = 0.7\) のとき、
\begin{align*} \sin\phi_1 &= \sqrt{1-\cos^2\phi_1} \\ &= \sqrt{1-0.7^2} \\ &= \sqrt{1-0.49} \\ &= \sqrt{0.51} \\ &\approx 0.714 \end{align*}
改善後: \(\cos\phi_2 = 0.95\) のとき、
\begin{align*} \sin\phi_2 &= \sqrt{1-\cos^2\phi_2} \\ &= \sqrt{1-0.95^2} \\ &= \sqrt{1-0.9025} \\ &= \sqrt{0.0975} \\ &\approx 0.312 \end{align*}
必要な進相コンデンサの容量 \(Q_C\) は次式で計算できます:
\begin{align*} Q_C &= P \times \left( \frac{\sin\phi_1}{\cos\phi_1} - \frac{\sin\phi_2}{\cos\phi_2} \right) \\ &\approx 100 \,kW \times \left( \frac{0.714}{0.7} - \frac{0.312}{0.95} \right) \\ &\approx 100 \,kW \times (1.02 - 0.329) \\ % 例題の丸めに合わせる &= 100 \,kW \times 0.691 \\ &\approx 69.1 \,kvar \end{align*}
したがって、必要な進相コンデンサの容量は約 69.1 kvar です。
補足:直接計算法(電気主任技術者試験での計算時間短縮法)
試験時間が限られている場合、以下の方法で素早く計算することもできます:
無効電力は \(Q = P\tan\phi\) で求められるため、
改善前の無効電力: \(Q_1 = P\tan\phi_1 = 100 \times 1.02 = 102 \,kvar\)
改善後の無効電力: \(Q_2 = P\tan\phi_2 = 100 \times 0.329 = 32.9 \,kvar\)
必要なコンデンサ容量: \(Q_C = Q_1 - Q_2 = 102 - 32.9 = 69.1 \,kvar\)
この方法では、三角関数の計算を最小限に抑えることができます。
力率改善による経済効果
力率改善には以下のような経済効果があります:
- 電力損失の減少:前述の通り、力率改善によって電流が減少し、\(I^2R\) 損失が大幅に削減されます。
- 設備容量の有効利用:同じ設備容量でより多くの有効電力を送電できるようになります。
- 電気料金の削減:多くの電力会社では、力率が基準値(一般的に85〜90%)を下回る場合、割増料金を請求する「力率割引・割増制度」を設けています。力率改善によって、この割増料金を避けたり、割引を受けたりすることができます。
- 電圧降下の減少:力率改善によって電圧品質が向上し、電圧降下に関連するトラブルが減少します。
力率改善による投資回収計算
力率改善設備の投資回収期間は以下の式で概算できます:
\[\text{投資回収期間} = \frac{\text{設備投資額}}{\text{年間節約額}}\]
年間節約額は、電力損失減少による節約と電気料金の力率割引による節約の合計です。
力率改善における注意点
・過補償に注意すること(進み力率になりすぎると電圧上昇や不安定化を引き起こす可能性がある)
・高調波環境下では、共振現象を避けるための対策が必要
・負荷変動が大きい場合は、自動力率調整装置の設置を検討
・コンデンサの経年劣化に注意し、定期的な点検と容量測定を実施
・系統全体のバランスを考慮した力率改善計画を立てること
試験対策のための覚えておくべき数値
第三種電気主任技術者試験では、頻出の力率値に対する \(\sin\phi\) と \(\tan\phi\) の値を素早く計算できることが重要です。以下の表を覚えておくと計算時間を短縮できます:
| 力率 \(\cos\phi\) | \(\sin\phi\) | \(\tan\phi\) |
|---|---|---|
| 1.0 | 0.0 | 0.0 |
| 0.95 | 0.312 | 0.329 |
| 0.9 | 0.436 | 0.484 |
| 0.85 | 0.527 | 0.620 |
| 0.8 | 0.6 | 0.75 |
| 0.75 | 0.661 | 0.882 |
| 0.7 | 0.714 | 1.02 |
| 0.6 | 0.8 | 1.33 |
| 0.5 | 0.866 | 1.73 |
演習問題:力率改善による経済効果
工場の受電設備において、平均負荷が 500 kW、力率が 0.75(遅れ)である。この力率を 0.95(遅れ)まで改善した場合:
(1) 必要な進相コンデンサの容量
(2) 受電電流の減少率
(3) 送電線損失(\(I^2R\))の減少率
を求めなさい。
解答:
(1) 必要な進相コンデンサの容量
上記の表から、\(\cos\phi_1 = 0.75\) のとき \(\tan\phi_1 = 0.882\)、\(\cos\phi_2 = 0.95\) のとき \(\tan\phi_2 = 0.329\) です。
\begin{align*} Q_C &= P(\tan\phi_1 - \tan\phi_2) \\ &= 500 \,kW \times (0.882 - 0.329) \\ &= 500 \,kW \times 0.553 \\ &= 276.5 \,kvar \end{align*}
したがって、必要な進相コンデンサの容量は約 276.5 kvar です。
(2) 受電電流の減少率
力率改善前後の電流比は:
\begin{align*} \frac{I_2}{I_1} &= \frac{\cos\phi_1}{\cos\phi_2} \\ &= \frac{0.75}{0.95} \\ &= 0.789 \end{align*}
つまり、電流は改善前の 78.9% になります。
電流の減少率は:
\begin{align*} \text{減少率} &= (1 - 0.789) \times 100\% \\ &= 21.1\% \end{align*}
(3) 送電線損失の減少率
送電線の損失は電流の2乗に比例するため:
\begin{align*} \frac{P_{loss,2}}{P_{loss,1}} &= \left(\frac{I_2}{I_1}\right)^2 \\ &= (0.789)^2 \\ &= 0.623 \end{align*}
つまり、損失は改善前の 62.3% になります。
損失の減少率は:
\begin{align*} \text{減少率} &= (1 - 0.623) \times 100\% \\ &= 37.7\% \end{align*}
したがって、力率改善によって送電線損失は約 37.7% 減少します。
4. 応用と実例
4.1 送電線路の運用と保護
送電線路は電力系統の重要な構成要素であり、安定した電力供給を維持するためには適切な運用と保護が不可欠です。
送電線路で発生する主な障害
送電線路では様々な障害が発生します。第三種電気主任技術者試験では、これらの障害メカニズムと対策について出題されることが多いため、詳細な理解が求められます。
- 雷害:雷撃による過電圧や絶縁破壊
- 短絡事故:相間短絡、地絡など
- 断線事故:暴風や着氷などによる断線
- 汚損事故:がいしの汚損による絶縁低下
- 過負荷:定格を超える電流による過熱
- 鳥獣害:鳥や小動物による短絡
雷害のメカニズムと対策
雷害は送電線路の最も重要な障害の一つで、特に日本のような雷活動が活発な地域では重要な対策課題です。雷害には主に以下の種類があります:


- 直撃雷:雷が直接送電線や鉄塔に落雷する現象
- フラッシュオーバー:架空地線や鉄塔への雷撃により、鉄塔の電位が上昇し、がいし部分でアーク放電(フラッシュオーバー)が発生する現象。鉄塔の接地抵抗が高いと発生しやすい。
- 逆フラッシュオーバー:雷撃電流が鉄塔を通じて大地に流れる際、鉄塔の電位上昇により、鉄塔から電線方向へフラッシュオーバーが発生する現象。特に接地抵抗が高い場合に問題となる。
- シールド失敗:架空地線による雷遮蔽(シールド)が失敗し、雷が直接電力線に落雷する現象。保護角が適切でない場合に発生する。
- 誘導雷:近傍への落雷により電磁誘導現象で送電線に過電圧が発生する現象
- 静電誘導:雷雲の電荷により送電線に静電誘導で電荷が誘起される現象
- 電磁誘導:雷電流の急激な変化により送電線に電磁誘導で過電圧が発生する現象


雷害発生時の現象
雷害発生時には以下のような諸現象が観察されます:
・がいし連での閃絡(フラッシュオーバー)
・電線間の相間短絡
・電線と大地間の地絡
・遮断器の動作(保護リレーの応動による)
・自動再閉路装置の動作(一時的な故障の場合)
・避雷器の動作(雷サージ電流の流出)
雷害に対する対策
| 対策 | 内容 | 効果・特徴 |
|---|---|---|
| 架空地線の設置 | 送電線の上部に接地された金属線を張り、雷撃を受け止める | ・直撃雷を防止(遮蔽効果) ・保護角(遮へい角)は通常45度以下に設定 ・OPGW(光ファイバー複合架空地線)も広く使用 |
| がいし連数の増加 | がいしの数を増やして絶縁強度を向上させる | ・雷インパルス耐電圧の向上 ・雷害多発地域では標準より多く使用 ・コスト増加のデメリットあり |
| 避雷器の設置 | 過電圧を制限するために変電所や重要箇所に設置 | ・雷サージを大地に放流 ・酸化亜鉛形(ZnO)避雷器が主流 ・変電所引き込み部に必須 |
| 鉄塔接地抵抗の低減 | 鉄塔の接地抵抗を下げて逆フラッシュオーバーを防止 | ・一般地域:30Ω以下 ・雷害多発地域:10Ω以下 ・接地線の増設や接地棒の打ち込み、接地材の使用など |
| アークホーンの設置 | フラッシュオーバーの際のアーク発生位置を制御する | ・がいしや金具の損傷防止 ・アークの発生位置を制御 ・再閉路成功率向上に寄与 |
| 高速度再閉路の採用 | 雷撃による一時的な故障後に自動的に送電を再開 | ・一時的な雷害への有効な対策 ・一般的に0.3〜0.5秒程度の不動作時間を設定 ・系統安定度向上にも寄与 |

逆フラッシュオーバー発生の条件計算(試験対策)
雷撃電流 \(I\) [kA]、鉄塔接地抵抗 \(R\) [Ω]、がいしの雷インパルス耐電圧 \(V_{FO}\) [kV] とすると、逆フラッシュオーバーの発生条件は次式で表されます:
\[I \times R > V_{FO}\]
例えば、鉄塔接地抵抗が20Ω、がいしの雷インパルス耐電圧が1000kVの場合、逆フラッシュオーバーが発生する最小雷撃電流は:
\[I > \frac{V_{FO}}{R} = \frac{1000}{20} = 50 \, \text{kA}\]
このように、接地抵抗が低いほど、より大きな雷撃電流に耐えられることになります。
送電線の機械的障害:スリートジャンプ現象
送電線路では電気的障害だけでなく、機械的な障害も発生します。特に冬季の着氷や着雪による障害は重要な問題です。
- スリート(着氷):電線表面に氷が付着する現象
- 着氷の種類:霧氷(rime ice)、雨氷(glaze ice)、樹氷(hard rime)など
- 発生条件:気温が0℃前後、湿度が高く、風が適度にある条件
- 問題点:重量増加による機械的負荷増大、風圧面積増加による風荷重増大
- スリートジャンプ(着氷脱落/氷雪跳動):電線に付着した氷雪が突然落下することで、電線が急激に跳ね上がる現象
- 発生メカニズム:
- 電線に氷雪が付着し、重量で弛度(たるみ)が増加
- 気温上昇や日照などにより、一部の氷雪が脱落
- 重量減少により電線が急激に跳ね上がる
- この振動が波及して連鎖的に着氷脱落が進行
- 問題点:
- 相間短絡や地絡事故の発生
- 電線や金具への機械的衝撃による損傷
- 振動によるがいし破損や鉄塔部材の疲労
- 発生メカニズム:
- ギャロッピング(電線舞い):風による電線の大振幅振動現象
- 発生メカニズム:非対称形状になった着氷電線に風が作用すると、揚力が発生して上下振動が始まる
- 特徴:振幅が大きく(数メートルに達することも)、周期が長い(数秒〜十数秒)
- 問題点:相間短絡、機械的疲労、地絡など

スリートジャンプ・ギャロッピング対策
| 対策 | 内容 | 特徴・効果 |
|---|---|---|
| 相間スペーサの設置 | 相間に絶縁性のスペーサを取り付け、電線間隔を保持 | ・相間短絡防止に有効 ・振動そのものは抑制できない |
| ダンパの設置 | 電線に振動減衰装置を取り付ける | ・振動エネルギーを吸収 ・ストックブリッジダンパ、スパイラルダンパなど |
| 相導体間隔の拡大 | 複導体の場合、導体間隔を広げる | ・振動時の相間短絡リスク低減 ・風による空気力学的特性の改善 |
| 電線張力の最適化 | 電線の張力を適切に設定する | ・高張力にすると弛度が小さくなり振動影響が低減 ・過度の張力は金具・支持物への負担増加 |
| 着氷防止対策 | 電線への着氷を防止する技術 | ・電線ヒーター ・撥水・撥氷コーティング ・電線振動装置 |
| 特殊電線の採用 | 断面形状の工夫により空力特性を改善 | ・8の字型断面電線 ・表面に凹凸をつけた電線 ・ねじれ電線 |
がいしの汚損障害
がいし(碍子)の表面汚損は、絶縁性能を低下させ、送電線事故の重要な原因となります。特に沿岸部や工業地帯では深刻な問題となります。
- 汚損の種類:
- 塩害汚損:海塩粒子の付着による汚損(沿岸部)
- 工業汚損:工場排ガス中の粉塵・化学物質による汚損(工業地帯)
- 農業汚損:農薬散布や砂埃などによる汚損(農業地域)
- 自然汚損:砂塵や花粉などの自然物質による汚損
- 汚損フラッシュオーバーの発生メカニズム:
- がいし表面に導電性物質(塩分や粉塵)が付着
- 湿度上昇(霧、雨、結露など)により汚損層が湿潤化
- 表面漏れ電流の発生と増加
- 漏れ電流による発熱でドライバンド(乾燥帯)形成
- ドライバンドでの部分アーク発生
- 部分アークの進展によるフラッシュオーバー
- 汚損度の評価指標:
- 等価塩分付着密度(ESDD: Equivalent Salt Deposit Density):がいし表面の塩分付着量 [mg/cm²]
- 漏れ電流密度:単位面積あたりの漏れ電流 [μA/cm²]
- 汚損耐圧比:汚損時の耐電圧/清浄時の耐電圧
がいし汚損対策
| 対策 | 内容 | 特徴・効果 |
|---|---|---|
| がいし洗浄 | 定期的にがいし表面を洗浄する | ・高圧水やブラシによる物理的洗浄 ・活線洗浄技術の発達 ・コストと労力がかかる |
| シリコーン塗布がいし | がいし表面にシリコーン系撥水剤を塗布 | ・水滴の形成を防止(撥水性) ・汚損物の付着抑制 ・定期的な塗り直しが必要 |
| ポリマーがいし | シリコーンゴムなどの高分子材料製がいし | ・優れた撥水性 ・軽量で施工が容易 ・紫外線劣化に注意が必要 |
| 長幹がいし | がいしの漏れ距離を増加させたがいし | ・単位電圧あたりの漏れ距離が長い ・重量増加のデメリット |
| 霧がいし | 複雑なひだを持つ特殊形状のがいし | ・漏れ距離の増加 ・雨による自然洗浄効果 ・汚損に強い |
| 耐塩害用装置 | 塩害地域用の特殊な保護装置 | ・洗浄装置の常設 ・がいしカバー ・防風防塵バリア |
汚損がいしの漏れ距離計算(試験対策)
汚損地域におけるがいしの必要漏れ距離は以下の式で概算できます:
\[L = k \times U \,\, [\text{mm}]\]
ここで、
\(L\) = 必要漏れ距離 [mm]
\(U\) = 最高運転電圧 [kV]
\(k\) = 汚損度に応じた係数 [mm/kV](軽汚損:16〜20、中汚損:20〜25、重汚損:25〜31、特殊重汚損:31以上)
例えば、重汚損地域で77kVの送電線の場合:
\[L = 28 \times 77 = 2156 \,\, [\text{mm}]\]
したがって、少なくとも2156mmの漏れ距離を持つがいしを選定する必要があります。
その他の送電線障害
送電線路で発生するその他の主要な障害と対策を以下に示します:
- 風害:強風による電線振動や共振
- 対策:振動ダンパ設置、電線張力調整、耐風設計の最適化
- 鳥獣害:鳥や小動物による短絡や地絡
- 原因:大型鳥類の営巣、鳥の糞の付着、小動物の侵入など
- 対策:鳥害防止装置(バードガード)、忌避装置、絶縁カバーの設置
- 樹木接触:送電線近傍の樹木との接触による地絡
- 対策:定期的な伐採・剪定、送電線下の保安伐採、絶縁電線の採用
- 金具の疲労破断:振動による金具の疲労破壊
- 対策:定期的な点検、アーマロッド設置、疲労対策型金具の採用
- コロナ放電(電線皮膜放電):導体表面での部分放電現象
- 発生メカニズム:
- 送電線表面の電界強度が空気の絶縁破壊強度(約30kV/cm)を超えると発生
- 特に凹凸や突起、傷のある部分で局所的に電界が集中して発生しやすい
- 湿度が高い時や雨・霧の時には発生が顕著になる(臨界電圧が低下)
- 電圧が高いほど発生しやすく、特に275kV以上の超高圧送電線では重要な問題
- コロナ放電の臨界電圧(ピーク値):ピークス(Peek's)の実験式で推定可能
- \[V_c = m_0 \cdot m_r \cdot \delta \cdot r \cdot \ln\frac{D}{r} \cdot E_0 \,\, [kV]\]
- ここで、\(m_0\):導体表面状態係数(平滑な導体:1.0、より線:0.82〜0.87)
- \(m_r\):気象条件係数(晴天時:1.0、雨天時:0.7〜0.8)
- \(δ\):空気密度係数(標準状態:1.0)
- \(r\):導体半径 [cm]
- \(D\):等価導体間距離 [cm]
- \(E_0\):空気の臨界電界強度(約30kV/cm)
- 影響と問題点:
- コロナ損失:部分放電によって電力が熱や光として失われる
- 雨天時には晴天時の10〜100倍に増加
- 電圧の2.5〜3.0乗に比例して増加
- 特に高電圧送電線では無視できない損失(数百kW/km)
- コロナ損失の概算式:\[P_c = 242 \cdot (f+25) \cdot \sqrt{\frac{r}{D}} \cdot (V-V_c)^2 \times 10^{-5} \,\, [kW/km/相]\]
- 可聴雑音(AN: Audible Noise):
- 放電に伴う空気の膨張収縮による騒音(ブーンという低周波ハム音)
- 特に雨天時に顕著(水滴が電界集中点となる)
- 周辺環境への騒音公害の原因となる(30〜60dB程度)
- 夜間の静寂時には特に問題となりやすい
- 無線障害(RI: Radio Interference):
- 放電に伴う広帯域電磁波ノイズによる無線通信障害
- AM放送帯(0.5〜1.5MHz)で特に影響が大きい
- テレビ、ラジオ、通信設備への干渉
- 距離に応じて減衰(距離の2乗に反比例)
- テレビ障害(TVI: Television Interference):
- VHF帯域(30〜300MHz)のテレビ放送への干渉
- 画面のちらつきやノイズとして現れる
- オゾン生成:
- 放電によって大気中の酸素からオゾン(O₃)が生成
- 環境への影響や金属部の腐食促進
- 特有の刺激臭による周辺環境への影響
- 電線表面腐食:
- 長期間のコロナ放電による導体表面の劣化
- 硝酸(HNO₃)の生成による金属腐食
- アルミニウム導体の場合、表面酸化による接触抵抗増加
- コロナ損失:部分放電によって電力が熱や光として失われる
- コロナ放電への対策:
- 導体径の増大:
- 導体表面の電界強度は半径に反比例するため、太い導体ほどコロナが発生しにくい
- 一般的に500kV級では直径40mm以上の導体が使用される
- ただし、重量増加やコスト増加のデメリットがある
- 複導体方式の採用:
- 一相あたり複数の導体(2〜4導体が一般的、最大8導体)を適切な間隔(通常20〜40cm)で配置
- 等価的な導体径の増大効果(例:2導体なら約1.5倍の効果)
- 電界分散による表面電界強度低減
- 複導体の等価半径:\[r_{eq} = \sqrt[n]{r \cdot a^{n-1}}\](\(r\):素導体半径、\(a\):導体間隔、\(n\):導体数)
- スペーサによる導体間隔の維持が必要
- 導体表面の平滑化:
- 平滑化導体(アルミより線表面を滑らかに加工)の採用
- 表面傷の防止と定期点検
- 金具接続部の電界緩和処理
- コロナリング/コロナシールドの設置:
- 電界集中が起こりやすい端部や金具に取り付ける環状または球状の金属部品
- 局所的な電界集中を緩和し、コロナ発生を抑制
- 特に変電所端子や接続部で使用
- 相間距離の最適化:
- 相間距離を適切に設定することで電界分布を最適化
- 非対称配置よりも対称配置が有利
- 表面処理技術:
- 導体表面への特殊コーティング
- 疎水性・撥水性材料の適用(水滴による電界集中防止)
- 導体径の増大:
- コロナ問題の評価方法:
- 実験室試験:小規模モデルでのコロナ特性評価
- 実規模試験:実際の送電線と同様の構成での評価
- 計算機シミュレーション:有限要素法などによる電界計算
- 測定指標:
- コロナ損失 [kW/km/相]
- 可聴雑音レベル [dB(A)]
- 無線障害レベル [dB(μV/m)]
- コロナ放電に関する規制と基準:
- 電力会社の設計基準:各電圧階級に応じたコロナ対策要件
- 環境基準:騒音に関する環境基準(夜間40〜50dB以下など)
- 国際基準:IEEE、IEC、CIGREなどの国際規格・ガイドライン
- 無線障害規制:送電線からの距離に応じた許容電界強度
- 電圧階級別のコロナ対策例:
電圧階級 一般的な対策 導体構成例 〜154kV 単一ACSR導体で十分 ACSR 160mm²〜410mm²(単導体) 275kV 複導体方式が一般的 ACSR 410mm²×2導体 500kV 多導体方式が必須 ACSR 410mm²×4導体、間隔40cm 1000kV以上 特殊多導体方式 ACSR 810mm²×8導体、特殊配置 - 第三種電気主任技術者試験対策ポイント:
- コロナ放電の発生条件(臨界電界強度:約30kV/cm)
- コロナ損失は電圧の2.5〜3.0乗に比例すること
- 雨天時には晴天時の10〜100倍のコロナ損失が発生すること
- 複導体方式の原理と等価半径の概念
- 電圧階級に応じた導体構成の違い
- コロナによる主な問題(損失、騒音、無線障害など)
- 発生メカニズム:
第三種電気主任技術者試験対策のポイント
送電線障害に関する試験対策として、以下の点を重点的に理解しておきましょう:
・雷害の種類と発生メカニズム(特に直撃雷と誘導雷の違い)
・逆フラッシュオーバーの条件と対策(特に接地抵抗低減の重要性)
・がいし汚損の種類と汚損フラッシュオーバーのメカニズム
・スリートジャンプとギャロッピングの違いと対策
・障害別の主要対策技術の特徴と適用条件
・高速度再閉路方式の効果と適用条件
送電線路の保護方式
送電線路の保護には、以下のような方式が用いられます:
| 保護方式 | 概要 | 特徴 |
|---|---|---|
| 過電流保護 | 定格を超える電流を検出して遮断 | ・構成が簡単 ・短い線路に適用 ・選択性に劣る |
| 距離保護 | 故障点までの電気的距離(インピーダンス)を検出して遮断 | ・高い選択性 ・バックアップ保護が可能 ・中長距離線路に適用 |
| 方向保護 | 故障電流の方向を検出して遮断 | ・環状網やループ系統に適用 ・選択性が高い |
| 比率差動保護 | 保護区間の両端の電流の差を検出して遮断 | ・高い選択性と感度 ・通信回線が必要 ・内部故障のみに動作 |
| パイロットリレー保護 | 通信回線を利用して両端の情報を交換し、協調動作 | ・高速度保護が可能 ・選択性が高い ・通信回線が必要 |
保護リレーシステムの条件
保護リレーシステムは以下の条件を満たす必要があります:
・高速性:故障を速やかに検出し、除去する
・選択性:故障区間のみを選択的に遮断する
・感度:小さな故障も確実に検出する
・信頼性:必要なときに確実に動作し、不要なときは動作しない
・経済性:保護の目的に対して過剰なコストをかけない
保護リレーと遮断器
保護システムの主要機器である保護リレーと遮断器は、電力系統を事故から守るための最重要設備です。第三種電気主任技術者試験では、これらの設備に関する問題が頻出するため、詳細な理解が必要です。
保護リレーの種類と特徴
保護リレーは、検出する電気量や保護原理によって以下のように分類されます:
| 分類 | リレーの種類 | 主な用途・特徴 |
|---|---|---|
| 電流リレー | 過電流リレー(OCR) | 設定値を超える電流を検出して動作。短絡・過負荷保護に使用。 |
| 地絡過電流リレー(OCGR) | 零相電流(地絡電流)を検出して動作。地絡事故保護に使用。 | |
| 方向過電流リレー(DOCR) | 特定方向の過電流のみに動作。環状系統や並列回線の保護に有効。 | |
| 比率差動リレー | 保護区間の入出力電流差を検出。変圧器・発電機・母線保護に使用。 | |
| 電圧リレー | 過電圧リレー(OVR) | 設定値を超える電圧を検出。過電圧保護・地絡検出に使用。 |
| 不足電圧リレー(UVR) | 電圧が設定値以下になると動作。モーター保護や系統分離に使用。 | |
| 地絡方向リレー | 零相電圧と零相電流の位相関係から地絡方向を検出。 | |
| インピーダンスリレー | 距離リレー | 故障点までのインピーダンスを測定。送電線保護の主保護として使用。 |
| リアクタンスリレー | 回路のリアクタンス成分のみを測定。短い送電線の保護に適する。 | |
| 周波数リレー | 低周波リレー(UFR) | 周波数低下を検出。負荷遮断や系統分離に使用。 |
| 高周波リレー(OFR) | 周波数上昇を検出。発電機の回転速度上昇保護などに使用。 | |
| パイロットリレー | 位相比較リレー | 線路両端の電流位相を比較。通信回線を使用した高速保護。 |
| 方向比較リレー | 線路両端の電流方向を比較。通信回線を使用した高速保護。 |
保護リレーの動作原理と特性
1. 距離リレー(第三種電気主任技術者試験での頻出項目)
距離リレーは、電圧と電流の比(インピーダンス)から故障点までの電気的距離を算出して動作します。主に送電線保護に使用され、以下の特徴があります:
- 基本式:\(Z = \frac{V}{I}\)(インピーダンス = 電圧/電流)
- 動作範囲:設定インピーダンス(リーチ)以下で動作
- ゾーン設定:通常3ゾーン構成(第1ゾーン:自線路の80~85%、第2ゾーン:自線路+隣接線路の50%、第3ゾーン:第2ゾーン+さらに広いエリア)
- タイマー設定:第1ゾーンは瞬時動作(0~50ms)、第2ゾーンは0.3~0.5秒遅延、第3ゾーンは0.8~1.0秒遅延
この多段階の時限設定により、故障点に最も近いリレーが最も早く動作し、選択性が確保されます。
2. 比率差動リレー
比率差動リレーは、保護区間の両端の電流の差を比率として検出します。以下の特徴があります:
- 基本原理:正常時は \(I_1 = I_2\)、内部故障時は \(I_1 \neq I_2\)
- 動作特性:差電流(\(I_d = |I_1 - I_2|\))と拘束電流(\(I_r = \frac{|I_1| + |I_2|}{2}\))の比率で判定
- スロープ特性:外部故障時の誤動作防止のため、拘束電流が大きいほど差動電流の動作閾値を上げる特性
比率差動リレーは変圧器保護の主保護として広く使用されており、内部故障に対して高感度でありながら、外部故障時の誤動作を防止できます。
遮断器(CB: Circuit Breaker)の種類と特徴
遮断器は、保護リレーからの指令を受けて故障区間を系統から切り離す重要な機器です。大電流の遮断能力と高速動作が要求されます。
| 分類 | 遮断器の種類 | 主な特徴・用途 |
|---|---|---|
| ガス遮断器 | SF6ガス遮断器(GCB) | ・六フッ化硫黄ガスの優れた絶縁・アーク消弧性能を利用 ・現在の特別高圧遮断器の主流 ・遮断容量が大きく、遮断時間が短い ・保守点検の頻度が少ない ・環境への配慮(SF6ガスは温室効果ガス)が必要 |
| 気中遮断器(ACB) | ・大気圧の空気をアーク消弧媒体とする ・低圧・高圧用途に使用 ・構造が簡単で信頼性が高い ・大容量遮断には不向き |
|
| 真空遮断器(VCB) | ・真空中でのアーク消弧特性を利用 ・主に3~36kVの高圧系統で使用 ・小型で遮断性能が優れている ・再起電圧が高くなりやすい ・保守点検が容易 |
|
| 油遮断器 | 大量油遮断器(OCB) | ・絶縁油中でアークを消弧 ・タンク全体に油を充填 ・遮断時の爆発・火災のリスクがある ・現在はほとんど使用されていない |
| 少量油遮断器(MOCB) | ・消弧室のみに油を充填 ・大量油遮断器より安全性が向上 ・小型化が可能 ・老朽設備の更新により減少中 |
|
| ガス絶縁開閉装置(GIS) | ・SF6ガスで絶縁された金属容器内に遮断器・断路器・接地開閉器等を一体収納 ・コンパクトで信頼性が高い ・設置面積が小さく、塩害・公害の影響を受けにくい ・特別高圧変電所で広く採用 |
遮断器の重要特性
・定格遮断電流:遮断器が安全に遮断できる最大短絡電流値(kA)
・定格電圧:遮断器の絶縁設計の基準となる電圧(kV)
・定格遮断時間:事故検出から遮断完了までの時間(サイクル数で表示、例:2サイクル=33ms@60Hz)
・短時間耐電流:遮断器が短時間(通常1秒)耐えられる最大電流(kA)
・投入電流:遮断器が安全に投入できる最大電流(通常は定格遮断電流の2.5倍程度)
・遮断責務:遮断器が負担する電気的ストレス(直流成分、過渡回復電圧など)
保護協調の原理
保護リレーシステムの選択性を確保するために、保護協調が重要です。保護協調とは、事故時に最も事故点に近い保護装置のみが動作するように、各保護装置の動作特性(感度と時限)を調整することです。
- 時限協調:上位系統側から下位系統側に向かって動作時間を短くする方式。事故点に近い遮断器から順に動作するようにタイマーを設定します。
- 電流協調:上位系統側の動作電流値を下位系統側より大きく設定する方式。系統構成によっては適用が難しい場合があります。
- 方向協調:環状系統やループ系統では、故障電流の方向を検出して選択性を確保します。
- ゾーン協調:距離リレーにおけるゾーン設定とタイマー設定の組み合わせによる協調方式です。
保護協調の計算例(第三種電気主任技術者試験対策)
放射状の配電系統において、上位系統から順に遮断器A、B、Cがあり、それぞれに過電流リレーが設置されている。最下流の遮断器Cの動作時間を0.3秒とする場合、上位の遮断器B、Aの時限設定はどうすべきか。ただし、保護協調時間差は0.2秒以上必要とする。
解答:
保護協調の原則に従い、下位から上位に向かって時限を長くします。
遮断器Cの動作時間:0.3秒
遮断器Bの動作時間:0.3 + 0.2 = 0.5秒
遮断器Aの動作時間:0.5 + 0.2 = 0.7秒
これにより、故障発生時には最も故障点に近い遮断器のみが動作し、選択性が確保されます。
高速度遮断方式
送電線路の保護では、系統安定度の維持や設備保護のために高速度遮断が重要です。特に重要な送電線路では、以下のような高度な保護・遮断方式が採用されています:
高速度再閉路方式(自動再閉路方式)
送電線の故障の約80%は一時的な故障(雷撃による短絡など)です。高速度再閉路方式は、このような一時的な故障に対応するために、一旦遮断した後に自動的に再投入する方式です。
- 動作シーケンス:
- 故障検出(リレー動作)
- 遮断器トリップ(故障区間遮断)
- 不動作時間(アークの自己消弧のための時間)
- 遮断器再投入(自動再閉路)
- 故障が継続している場合はロックアウト(再投入禁止)
- 不動作時間(デッドタイム):
- 高速再閉路:0.2~0.5秒(アークの離子化消滅時間)
- 低速再閉路:数秒~数十秒(運用上の理由で長めに設定)
- 再閉路成功率:
- 架空送電線では約70~80%(特に雷害が多い地域では効果が高い)
- 地中送電線では効果が低いため、通常は採用されない
- 系統安定度への影響:
- 故障継続時間が短くなるため、系統の安定度維持に効果的
- 特に重要な連系線では、系統安定度維持のために不可欠
単相遮断方式
三相送電線路で単相地絡などの単相故障が発生した場合、故障相のみを遮断し、健全相は送電を継続する方式です。三相遮断方式と比較して以下の利点があります:
- 送電継続性の向上:
- 故障相のみの遮断により、残りの健全相(2相)で電力送電を一部継続できる
- 送電線路故障の約70~80%は単相地絡であるため、適用効果が高い
- 系統安定度の向上:
- 三相遮断に比べて系統の同期化力が維持されるため、安定度が向上
- 特に長距離・大容量送電線では効果が顕著
- 単相再閉路:
- 単相遮断と再閉路を組み合わせることで、さらに効果が向上
- 特に275kV以上の基幹系統で採用されることが多い
- 適用条件:
- 遮断器が単相操作可能であること(各相独立操作機構)
- 不平衡運転に対する系統の許容度があること
- 二次アークの消弧能力があること
二次アークとは
単相遮断後に残る健全相から、静電結合や電磁結合によって故障相に誘起される電流によって維持されるアークのことです。単相再閉路の成功には、このアークが自己消弧することが必要です。二次アーク消弧対策として、以下の方法があります:
・4脚鉄塔の採用(相間距離の拡大)
・アークホーン間隔の最適化
・中性点リアクトルの設置
・補償装置の設置
差動保護方式(線路差動保護)
送電線路の両端の電流を比較して保護区間内の故障を検出する方式です。通信回線を使用して両端の電流情報をリアルタイムで交換します。
- 特徴:
- 高速・高感度動作(10~20ms程度)
- 保護区間内の故障位置に関係なく同一感度で検出可能
- 方向判定が不要で、選択性に優れる
- 課題:
- 通信回線の信頼性に依存
- 通信遅延の補正が必要
- 設備コストが高い
- 適用:
- 特に重要な短距離送電線(20km程度まで)
- 地中送電線(ケーブル)保護
- 直流送電線の保護
試験対策:保護リレーと遮断器に関する問題例
送電線の保護リレーに関する次の記述のうち、誤っているものはどれか。
- 距離リレーは、故障点までの電気的距離(インピーダンス)を測定して動作するリレーであり、送電線保護の主保護として広く使用されている。
- 比率差動リレーは、保護区間の両端の電流の差を検出して動作するリレーであり、変圧器や発電機の内部故障保護に適している。
- 方向性リレーは、潮流の方向に関係なく設定値を超える電流が流れたときに動作するリレーであり、環状系統の保護に使用される。
- 地絡過電流リレーは、地絡電流(零相電流)を検出して動作するリレーであり、接地系統の地絡事故保護に使用される。
- 高速度再閉路方式は、送電線の一時的な故障(主に雷撃による)に対して有効な方式であり、系統安定度の向上に寄与する。
解答:3
方向性リレー(方向リレー)は、電流の方向(潮流方向)を判別して特定方向の過電流に対してのみ動作するリレーです。「潮流の方向に関係なく」という記述は誤りです。方向性リレーは、環状系統や並列回線など、故障点に対して複数の電流供給経路がある場合に、正しい故障区間のみを選択的に遮断するために使用されます。
デジタルリレーと保護システムの最新動向
従来の電磁リレーや静止形リレーに代わり、現在では多機能デジタルリレー(マイクロプロセッサリレー)が主流となっています。これらの最新技術には以下のような特徴があります:
- 多機能デジタルリレー:
- 一つのハードウェアで複数の保護機能を実現(過電流、距離、差動など)
- 自己診断機能による信頼性向上
- イベント記録やオシログラム記録機能
- 通信機能によるSCADAシステムとの連携
- 広域保護システム:
- PMU(位相計測装置)を用いた広域監視・保護
- 系統全体の安定度監視と連動した保護機能
- GPS同期による高精度時刻同期
- 適応型保護システム:
- 系統状態に応じて保護設定を自動調整
- AI・機械学習を活用した故障予測と保護
- 分散型電源の増加に対応した新しい保護概念
第三種電気主任技術者試験対策ポイント
保護リレーと遮断器に関する試験対策としては、以下の点を重点的に理解しておきましょう:
・各種保護リレーの動作原理と適用箇所
・距離リレーのゾーン設定と時限協調
・比率差動リレーの動作特性(差電流と拘束電流の関係)
・遮断器の種類と特性の違い(特にSF6ガス遮断器と真空遮断器)
・高速度再閉路方式の動作シーケンスと不動作時間
・単相遮断方式と三相遮断方式の違いと適用条件
・保護協調の基本原則(時限協調、電流協調、方向協調)
4.2 中性点接地方式
中性点接地方式は、三相交流系統の中性点(Y結線の場合の中心点)と大地との接続方法を指します。選択する接地方式によって、地絡事故時の過電圧や地絡電流の大きさが異なります。
主な中性点接地方式
日本の電力系統で採用されている主な中性点接地方式は以下の通りです:
| 接地方式 | 概要 | 特徴 | 適用範囲 |
|---|---|---|---|
| 直接接地方式 | 中性点を直接大地に接続 | ・地絡電流が大きい ・地絡時の過電圧が小さい ・保護リレーの検出が容易 |
・特別高圧系統(154kV以上) ・低圧系統(100/200V) |
| 抵抗接地方式 | 中性点と大地の間に抵抗を挿入 | ・地絡電流を制限 ・地絡時の過電圧を抑制 ・アークの自己消弧は期待できない |
・特別高圧系統(22kV〜77kV) |
| リアクトル接地方式 (消弧リアクトル) |
中性点と大地の間にリアクトルを挿入 | ・充電電流を相殺 ・地絡時のアークが自己消弧 ・保護リレーの検出が困難 |
・特殊な高圧系統 |
| 非接地方式 | 中性点を大地に接続しない | ・地絡電流が小さい(充電電流のみ) ・地絡時の健全相の対地電圧上昇 ・一線地絡で送電継続可能 |
・高圧系統(6.6kV) |
日本における中性点接地方式の適用
日本では、電圧階級によって以下のような中性点接地方式が一般的に採用されています:
・特別高圧(154kV以上):直接接地方式
・特別高圧(22kV〜77kV):抵抗接地方式
・高圧(6.6kV):非接地方式(一部抵抗接地方式)
・低圧(100/200V):直接接地方式(多くはTT方式またはTN方式)
地絡時の過電圧と地絡電流
各接地方式における地絡時の特性は以下の通りです:
非接地系統の一線地絡時の健全相電圧上昇
非接地系統で一線地絡が発生すると、健全相の対地電圧は線間電圧に上昇します:
\[V_{健全相-大地} = \sqrt{3} \times V_{相電圧} = V_{線間電圧}\]
直接接地系統の地絡電流
直接接地系統の地絡電流は、故障点の抵抗を無視すると以下のように計算できます:
\[I_g = \frac{3V_0}{Z_1 + Z_2 + Z_0}\]
ここで、
\(I_g\) = 地絡電流
\(V_0\) = 零相電圧
\(Z_1\) = 正相インピーダンス
\(Z_2\) = 逆相インピーダンス
\(Z_0\) = 零相インピーダンス
例題:非接地系統の健全相電圧上昇
三相3線式6.6kV(線間電圧)の高圧配電線において、一線地絡が発生した場合の健全相の対地電圧を求めなさい。
解答:
相電圧は \(V_{相電圧} = \frac{V_{線間電圧}}{\sqrt{3}} = \frac{6.6}{\sqrt{3}} = 3.81 \,kV\)
非接地系統で一線地絡が発生した場合、健全相の対地電圧は線間電圧に上昇します:
\begin{align*} V_{健全相-大地} &= \sqrt{3} \times V_{相電圧} \\ &= \sqrt{3} \times 3.81 \\ &= 6.6 \,kV \end{align*}
したがって、健全相の対地電圧は 6.6 kV となります。
4.3 高電圧工学の基礎
送電線路は高電圧で運用されるため、高電圧工学の基礎知識が重要です。特に絶縁協調と過電圧対策は、送電設備の信頼性確保に不可欠です。
絶縁協調と絶縁設計
絶縁協調とは、電力系統内の様々な機器の絶縁強度を調整し、過電圧が発生した場合に最も影響の少ない箇所で絶縁破壊が起こるように設計することです。
絶縁協調の考え方
・保護装置(避雷器など)は最も低い絶縁強度に設定
・自己復帰が困難な機器(変圧器など)は高い絶縁強度に設定
・自己復帰が容易な機器(空気絶縁区間など)は中間の絶縁強度に設定
絶縁設計では、以下の要素を考慮する必要があります:
- 運転電圧:通常運転時の連続電圧
- 一時的過電圧:地絡事故などによる数秒〜数分間続く過電圧
- 開閉過電圧:開閉操作時に発生する過電圧
- 雷過電圧:雷撃によって発生する過電圧
過電圧の種類と対策
送電線路で発生する主な過電圧とその対策は以下の通りです:
| 過電圧の種類 | 概要 | 特徴 | 主な対策 |
|---|---|---|---|
| 雷過電圧 | 雷撃による過電圧 | ・波頭長が短く、波高値が高い ・局所的に発生 ・確率的に発生 |
・架空地線の設置 ・避雷器の設置 ・がいし連数の増加 ・耐雷設計の強化 |
| 開閉過電圧 | 遮断器などの開閉動作時に発生 | ・波頭長が長く、波高値は比較的低い ・系統全体に伝搬 ・操作によって発生 |
・抵抗投入方式の採用 ・避雷器の設置 ・同期投入の採用 ・サージアブソーバの設置 |
| 一時的過電圧 | 地絡事故や負荷遮断時に発生 | ・商用周波数の過電圧 ・数秒〜数分間持続 ・系統条件によって発生 |
・中性点接地方式の選定 ・無効電力制御 ・保護リレーの適切な設定 |
雷過電圧の推定式(岸の式)
直撃雷による過電圧の推定には、岸の式が用いられます:
\[V = \frac{I_0 Z_0}{2} \,\, [V]\]
ここで、
\(V\) = 雷過電圧 [V]
\(I_0\) = 雷電流 [A]
\(Z_0\) = 送電線のサージインピーダンス [Ω]
避雷器の役割と特性
避雷器は、過電圧から電力設備を保護するための重要な機器です。主な特性は以下の通りです:
- 制限電圧:過電圧を制限するレベル
- 放電開始電圧:避雷器が動作を始める電圧
- 公称放電電流:避雷器が処理できる標準的な放電電流
- 定格電圧:避雷器に連続して印加できる最大電圧
現代の送電線路では、主に酸化亜鉛形(ZnO)避雷器が使用されています。これは非直線抵抗特性に優れ、放電ギャップを必要としないという利点があります。
避雷器の設置箇所
避雷器は以下の箇所に設置されることが多いです:
・変電所の主要機器(変圧器、遮断器など)の近く
・送電線路の引き込み部分
・開閉所の主要機器の近く
・特に雷害の多い地域の送電線路上
5. 演習問題
ここでは、送電分野に関する演習問題を解いて、理解を深めましょう。
問題1(基本計算問題)
抵抗 \(R = 3 \,\Omega\)、リアクタンス \(X = 4 \,\Omega\) の送電線路がある。この送電線路に三相平衡負荷を接続し、送電端から 10 MW(力率0.8遅れ)の電力を受電端で消費している。受電端の線間電圧が 66 kV のとき、以下の値を求めなさい。
- 線路電流
- 送電損失
- 送電端の線間電圧
解答:
与えられた条件:
- 送電線路の抵抗 \(R = 3 \,\Omega\)
- 送電線路のリアクタンス \(X = 4 \,\Omega\)
- 受電電力 \(P = 10 \,MW\)
- 力率 \(\cos\phi = 0.8\)(遅れ)
- 受電端線間電圧 \(V_R = 66 \,kV\)
(1) 線路電流の計算
三相回路の受電電力は \(P = \sqrt{3} V_R I \cos\phi\) で表されるので、線路電流 \(I\) は:
\begin{align*} I &= \frac{P}{\sqrt{3} V_R \cos\phi} \\ &= \frac{10 \times 10^6}{\sqrt{3} \times 66 \times 10^3 \times 0.8} \\ &= \frac{10 \times 10^6}{91.2 \times 10^3} \\ &= 109.6 \,A \end{align*}
(2) 送電損失の計算
三相回路の送電損失は \(P_{loss} = 3 I^2 R\) で計算できます:
\begin{align*} P_{loss} &= 3 \times I^2 \times R \\ &= 3 \times (109.6)^2 \times 3 \\ &= 3 \times 12,012.16 \times 3 \\ &= 108,109.44 \,W \\ &\approx 108.1 \,kW \end{align*}
(3) 送電端の線間電圧の計算
送電端電圧は、受電端電圧と電圧降下の和として計算できます。まず、\(\sin\phi\) を計算します:
\(\sin\phi = \sqrt{1-\cos^2\phi} = \sqrt{1-0.8^2} = \sqrt{0.36} = 0.6\)
次に、相電圧での電圧降下を計算します:
\begin{align*} \Delta V &= IR\cos\phi + IX\sin\phi \\ &= 109.6 \times 3 \times 0.8 + 109.6 \times 4 \times 0.6 \\ &= 262.8 + 262.8 \\ &= 525.6 \,V \end{align*}
受電端の相電圧は \(V_{R,相} = \frac{V_{R,線間}}{\sqrt{3}} = \frac{66,000}{\sqrt{3}} = 38,105 \,V\)
したがって、送電端の相電圧は:
\(V_{S,相} = V_{R,相} + \Delta V = 38,105 + 525.6 = 38,630.6 \,V\)
送電端の線間電圧は:
\(V_{S,線間} = \sqrt{3} \times V_{S,相} = \sqrt{3} \times 38,630.6 = 66,910 \,V \approx 66.9 \,kV\)
したがって、送電端の線間電圧は約 66.9 kV となります。
問題2(基本計算問題)
送電容量 100 MVA、送電距離 50 km の架空送電線路において、アルミ導体の断面積を 200 mm² から 400 mm² に増加させた場合、送電損失はどのように変化するか。ただし、導体の抵抗率は \(2.8 \times 10^{-8} \,\Omega \cdot m\) とし、力率は変化しないものとする。
解答:
導体の抵抗は断面積に反比例します。抵抗 \(R\) は以下の式で計算できます:
\[R = \rho \times \frac{l}{A}\]
ここで、
- \(\rho\) = 抵抗率 [\(\Omega \cdot m\)]
- \(l\) = 導体の長さ [m]
- \(A\) = 導体の断面積 [m²]
断面積を \(A_1 = 200 \,mm²\) から \(A_2 = 400 \,mm²\) に増加させると、抵抗の比は:
\begin{align*} \frac{R_2}{R_1} &= \frac{A_1}{A_2} \\ &= \frac{200}{400} \\ &= 0.5 \end{align*}
送電損失 \(P_{loss}\) は抵抗に比例するため:
\begin{align*} \frac{P_{loss,2}}{P_{loss,1}} &= \frac{R_2}{R_1} \\ &= 0.5 \end{align*}
したがって、導体の断面積を 200 mm² から 400 mm² に増加させると、送電損失は元の損失の 50%(半分)になります。
問題3(基本計算問題)
有効電力 5 MW、無効電力 4 Mvar(遅れ)の負荷に対して、力率を 0.95(遅れ)まで改善したい。必要な進相コンデンサの容量を求めなさい。また、力率改善による電流の減少率を計算しなさい。
解答:
与えられた条件:
- 有効電力 \(P = 5 \,MW\)
- 無効電力(改善前) \(Q_1 = 4 \,Mvar\)(遅れ)
- 改善後の力率 \(\cos\phi_2 = 0.95\)(遅れ)
改善前の力率を計算します:
\begin{align*} \cos\phi_1 &= \frac{P}{\sqrt{P^2 + Q_1^2}} \\ &= \frac{5}{\sqrt{5^2 + 4^2}} \\ &= \frac{5}{\sqrt{25 + 16}} \\ &= \frac{5}{\sqrt{41}} \\ &= \frac{5}{6.4} \\ &\approx 0.78 \end{align*}
改善後の無効電力 \(Q_2\) は、\(\tan\phi_2 = \frac{Q_2}{P}\) より:
\begin{align*} \tan\phi_2 &= \sqrt{\frac{1}{\cos^2\phi_2} - 1} \\ &= \sqrt{\frac{1}{0.95^2} - 1} \\ &= \sqrt{\frac{1}{0.9025} - 1} \\ &= \sqrt{1.108 - 1} \\ &= \sqrt{0.108} \\ &\approx 0.329 \end{align*}
したがって、改善後の無効電力は:
\begin{align*} Q_2 &= P \times \tan\phi_2 \\ &= 5 \times 0.329 \\ &= 1.645 \,Mvar \end{align*}
必要な進相コンデンサの容量 \(Q_C\) は、改善前と改善後の無効電力の差です:
\begin{align*} Q_C &= Q_1 - Q_2 \\ &= 4 - 1.645 \\ &= 2.355 \,Mvar \end{align*}
次に、力率改善による電流の減少率を計算します。
電流は皮相電力に比例し、電圧が一定の場合、皮相電力は \(S = \frac{P}{\cos\phi}\) で表されます。
改善前の皮相電力:
\begin{align*} S_1 &= \frac{P}{\cos\phi_1} \\ &= \frac{5}{0.78} \\ &\approx 6.41 \,MVA \end{align*}
改善後の皮相電力:
\begin{align*} S_2 &= \frac{P}{\cos\phi_2} \\ &= \frac{5}{0.95} \\ &\approx 5.26 \,MVA \end{align*}
電流の減少率は:
\begin{align*} \frac{I_2 - I_1}{I_1} \times 100\% &= \frac{S_2 - S_1}{S_1} \times 100\% \\ &= \frac{5.26 - 6.41}{6.41} \times 100\% \\ &= \frac{-1.15}{6.41} \times 100\% \\ &\approx -17.9\% \end{align*}
したがって、電流は約 17.9% 減少します。
問題(第三種電気主任技術者試験 類似問題)
架空送電線路の保護に関する以下の記述のうち、誤っているものを選びなさい。
- 距離リレーは、電圧と電流の比から故障点までのインピーダンス(距離)を算出して動作する。
- 比率差動リレーは、保護区間の両端の電流の差が設定値を超えたとき動作する。
- 地絡過電流リレーは、地絡電流が設定値を超えたとき動作する。
- 方向リレーは、電流の方向に関係なく、設定値を超える電流が流れたとき動作する。
- 高速度再閉路方式は、一時的な故障(雷撃など)の場合、一旦遮断した後に自動的に再投入する保護方式である。
解答:4
それぞれの記述について検討します:
- 正しい:距離リレーは、電圧と電流の比(インピーダンス)から故障点までの電気的距離を算出して動作します。
- 正しい:比率差動リレーは、保護区間の両端の電流の差が設定値を超えたとき動作します。内部故障の場合に電流の差が生じます。
- 正しい:地絡過電流リレーは、地絡電流(零相電流)が設定値を超えたとき動作します。
- 誤り:方向リレーは、電流の方向に応じて動作するリレーです。設定された方向(順方向または逆方向)の電流のみに対して動作し、電流の方向は電圧と電流の位相差から判断されます。したがって、「電流の方向に関係なく動作する」という記述は誤りです。
- 正しい:高速度再閉路方式は、一時的な故障(雷撃など)の場合、一旦遮断した後に自動的に再投入する保護方式です。これにより、永続的でない故障の場合に系統の連続性を維持できます。
したがって、誤っているのは選択肢4です。
問題(第三種電気主任技術者試験 類似問題)
三相3線式66kV送電線路において、A相が地絡した。この送電線路の中性点接地方式が非接地方式である場合、地絡後のB相及びC相の対地電圧として、最も適切なものを次の中から選びなさい。
- 約38kV
- 約66kV
- 約114kV
- 0V
- 変化しない
解答:2
三相3線式66kV送電線路では、相電圧(線間電圧と中性点間の電圧)は:
\begin{align*} V_{相電圧} &= \frac{V_{線間電圧}}{\sqrt{3}} \\ &= \frac{66}{\sqrt{3}} \\ &\approx 38.1 \,kV \end{align*}
非接地方式の送電線路で一相(A相)が地絡すると、地絡相(A相)の対地電圧はほぼ0Vとなり、健全相(B相およびC相)の対地電圧は線間電圧(66kV)に上昇します。
これは、地絡によって系統の中性点が移動するためです。非接地系統では、三相の対地静電容量が等しい場合、中性点は三相ベクトルの中心にありますが、一相が地絡すると地絡点が新たな中性点となり、健全相の対地電圧は線間電圧に等しくなります。
したがって、B相及びC相の対地電圧として最も適切なのは、「約66kV」(選択肢2)です。
問題(第三種電気主任技術者試験 類似問題)
送電線の絶縁設計に関する以下の記述のうち、誤っているものを選びなさい。
- 直接接地方式では、地絡事故発生時の過電圧が小さい。
- 雷過電圧に対しては、主に避雷器や架空地線による保護が有効である。
- 開閉過電圧を抑制するには、抵抗投入方式や同期投入方式が有効である。
- 酸化亜鉛形避雷器は、ギャップ形避雷器よりも制限電圧が高い。
- 絶縁協調は、系統内の各機器の絶縁強度を調整し、過電圧発生時に影響の少ない箇所で絶縁破壊が起こるように設計することである。
解答:4
それぞれの記述について検討します:
- 正しい:直接接地方式では、地絡事故発生時に故障相の電位が地絡点の電位にほぼ等しくなり、健全相の対地電圧の上昇が抑えられるため、過電圧が小さくなります。
- 正しい:雷過電圧に対しては、避雷器による電圧制限と架空地線による雷撃の遮蔽が有効な保護手段です。
- 正しい:開閉過電圧を抑制するには、遮断器の投入時に抵抗を直列に入れる抵抗投入方式や、電圧波形の特定の位相で投入する同期投入方式が有効です。
- 誤り:酸化亜鉛形(ZnO)避雷器は、従来のギャップ形避雷器よりも制限電圧が低いという特徴があります。これは、ZnO素子の非直線性が高く、放電ギャップを必要としないため、より精密な電圧制限が可能になっています。したがって、「制限電圧が高い」という記述は誤りです。
- 正しい:絶縁協調は、電力系統内の各機器の絶縁強度を調整し、過電圧発生時に影響の少ない箇所(自己復帰が容易な箇所など)で絶縁破壊が起こるように設計するという考え方です。
したがって、誤っているのは選択肢4です。
6. まとめ
送電分野の重要ポイント
本ページでは、第三種電気主任技術者試験の送電分野について学習しました。重要なポイントは以下の通りです:
- 送電線路の構成と設備
- 架空送電線路は建設コストが低く保守が容易だが、自然環境の影響を受けやすい
- 地中送電線路は自然環境の影響を受けにくく景観への影響が少ないが、建設コストが高い
- 送電方式とその特徴
- 交流送電は変圧が容易で一般的だが、長距離送電では損失が大きい
- 直流送電(HVDC)は長距離送電や海底ケーブルに適しているが、変換設備が複雑
- 複回線送電は信頼性が高いが、コストが高い
- 送電線路の電気的特性
- 送電損失は \(P_{loss} = 3I^2R\) で計算され、電圧を上げることで低減できる
- 電圧降下は \(\Delta V = IR\cos\phi + IX\sin\phi\) で近似でき、力率改善などで対策
- 力率改善には進相コンデンサや同期調相機が使用される
- 送電線路の運用と保護
- 保護リレーは選択性、高速性、感度、信頼性が求められる
- 距離リレー、比率差動リレー、方向リレーなどが使用される
- 高速度再閉路方式や単相遮断方式で供給信頼度を向上
- 中性点接地方式
- 直接接地方式は地絡電流が大きく、過電圧が小さい(154kV以上)
- 抵抗接地方式は地絡電流を制限する(22kV〜77kV)
- 非接地方式は地絡電流が小さいが、健全相の電圧が上昇する(6.6kV)
- 高電圧工学の基礎
- 絶縁協調は各機器の絶縁強度を調整して、影響の少ない箇所で絶縁破壊が起こるようにする
- 過電圧には雷過電圧、開閉過電圧、一時的過電圧があり、それぞれに対策が必要
- 避雷器は過電圧から電力設備を保護する重要な機器
第三種電気主任技術者試験での出題傾向
第三種電気主任技術者試験の送電分野では、主に以下のような問題が出題される傾向があります:
- 送電損失や電圧降下の計算問題
- 力率改善に関する計算問題
- 中性点接地方式に関する問題(特に地絡時の過電圧)
- 送電線路の保護方式に関する問題
- 送電線路の絶縁設計や過電圧対策に関する問題
これらの問題に対応するためには、基本的な公式や概念を理解するだけでなく、実際の計算問題を解く練習が重要です。本ページで紹介した演習問題を繰り返し解くことで、理解を深めることができます。
次の学習単元への橋渡し
送電分野の学習の次は、以下の関連分野について学習することをお勧めします:
- 変電分野:変圧器、遮断器、調相設備など、変電所の設備と運用
- 配電分野:配電線路の構成、電圧降下計算、保護協調など
- 電力系統:安定度、潮流計算、系統運用など
これらの分野を総合的に学習することで、電力系統全体についての理解が深まり、第三種電気主任技術者試験の電力科目に万全の対策をとることができます。
学習のポイント
・基本的な公式を理解し、応用できるようにする
・実際の計算問題を解く練習を重ねる
・送電、変電、配電の関連性を意識して学習する
・過去問を解いて出題傾向を把握する
・実務での応用を意識して学習することで理解が深まる