【第三種電気主任技術者試験】変圧器の完全解説

1. イントロダクション

電柱の上に取り付けられた灰色の箱、大きな発電所や変電所で見かける巨大な機器、家電製品やスマートフォンの充電器の中に入っている小さな部品—これらはすべて「変圧器」の一種です。変圧器は電気エネルギーの電圧を変換する重要な電気機器で、私たちの日常生活と産業活動を支える電力系統に不可欠な存在です。

イメージ図: 様々な種類の変圧器

身近な変圧器（柱上変圧器）

変圧器は電磁誘導の原理を利用して、ある交流電圧を別の交流電圧に変換します。この特性により、発電所で発生した高電圧の電力を、変電所で段階的に電圧を下げて、私たちの家庭や工場で使いやすい電圧に変換することができます。また、電子機器では小型の変圧器が使われ、家庭用の100Vや200Vの電圧を、電子回路に適した低い電圧に変換しています。

第三種電気主任技術者試験における重要性
変圧器に関する知識は、第三種電気主任技術者試験の「理論」と「機械」の両科目において重要な出題分野となっています。特に、変圧器の基本原理、等価回路、各種特性、結線方式などが頻出します。変圧器は電力系統において電圧変換を行う唯一の機器であり、電気設備の設計・運用・保守において必須の知識となります。

変圧器の最大の特徴は、可動部分がなく静止した状態で動作する「静止器」であることです。このため、回転機と比較して保守が容易で寿命が長いという利点があります。一方で、鉄心での鉄損や巻線での銅損などの損失があり、これらを最小化する設計が重要です。

この学習ページでは、変圧器の基本構造から始まり、動作原理、特性、応用と特殊変圧器まで、第三種電気主任技術者試験の対策として必要な内容を丁寧に解説していきます。電力系統における変圧器の役割と基本特性を理解することで、電気技術者としての基礎知識を身につけましょう。

2. 変圧器の基本構造

変圧器は主に「鉄心」と「巻線」から構成されています。これらの構造と役割を理解することが、変圧器の動作原理を理解する基礎となります。

2.1 鉄心の構造

鉄心は変圧器の磁気回路を形成する部分で、主に以下の種類があります：

積鉄心型：薄い珪素鋼板を積層した構造で、単相変圧器に多く使用されます
巻鉄心型：珪素鋼帯を巻いた構造で、三相変圧器などの大型変圧器に使用されます

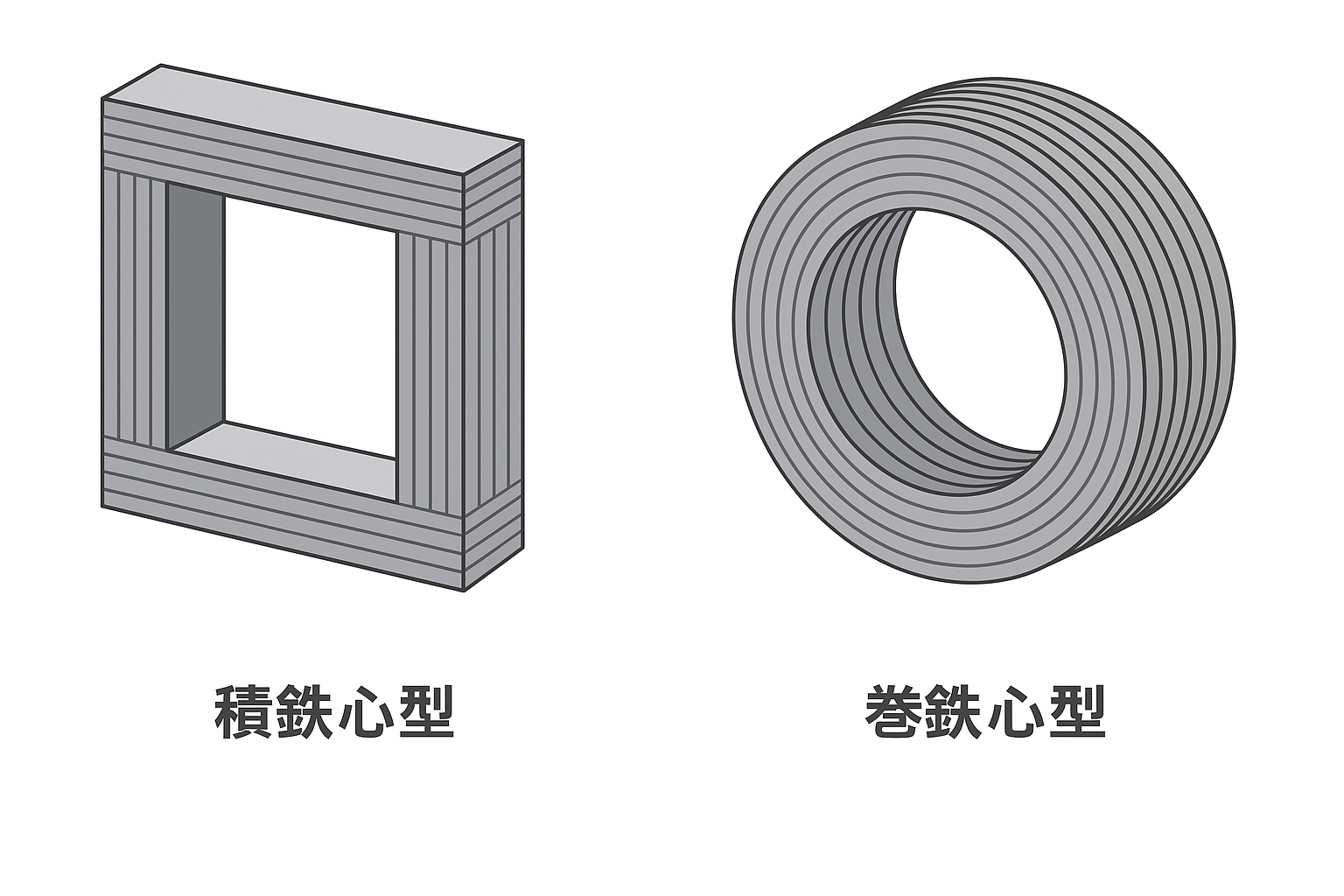
イメージ図: 鉄心の種類（左：積鉄心型、右：巻鉄心型）

鉄心の形状には、次のような種類があります：

円柱型（コア型）：巻線が鉄心の周りを取り囲む構造
角型（シェル型）：鉄心が巻線を取り囲む構造

珪素鋼板を積層する理由は、交流磁束による渦電流損失を低減するためです。通常、珪素鋼板の厚さは0.23〜0.35mm程度で、表面には絶縁処理が施されています。珪素鋼板には、磁気特性を向上させるために珪素が約3〜4.5%添加されています。

方向性珪素鋼板
大型の変圧器では、「方向性珪素鋼板」が使用されることが多いです。これは特定の方向（圧延方向）に磁化特性が優れており、鉄心の磁束方向と圧延方向を合わせることで、鉄損を低減し効率を向上させることができます。ただし、非方向性の珪素鋼板と比べて高価なため、小型変圧器では一般的に使用されません。

2.2 巻線の構造

変圧器の巻線は、電流を通して磁束を発生させたり、磁束の変化によって誘起電圧を発生させたりする役割を持ちます。巻線は主に2種類あります：

一次巻線（1次巻線）：電源側に接続される巻線
二次巻線（2次巻線）：負荷側に接続される巻線

イメージ図: 巻線の構造(鉄心に均等に巻かれたコイルで構成。)

巻線の構造には、次のような種類があります：

円筒巻線：円筒状に巻かれた構造で、機械的強度が高く、大電流に適しています
ディスク巻線：ディスク状に巻かれた構造で、高電圧巻線に適しています
連続巻線：連続して巻かれた構造で、小型変圧器に使用されます
ホイール巻線：車輪のスポークのように放射状に巻かれた構造です

巻線の材料は、一般的には銅が使用されますが、コストや重量の削減が必要な場合にはアルミニウムが使用されることもあります。巻線には絶縁処理が施され、巻線間や鉄心との間の絶縁が確保されています。

巻線の絶縁
変圧器の巻線には、次のような絶縁方式が採用されています：

導体絶縁：エナメル線やガラス繊維被覆など、導体自体の絶縁
層間絶縁：巻線の層間に挿入される絶縁物（絶縁紙など）
巻線間絶縁：1次巻線と2次巻線の間の絶縁（絶縁筒など）
対地絶縁：巻線と鉄心、タンクなどとの間の絶縁

大型の油入変圧器では、絶縁油が絶縁材料として使用されます。一方、乾式変圧器では、エポキシ樹脂などの固体絶縁材料が使用されます。

2.3 変圧器の種類

変圧器は、用途や構造によって様々な種類に分類されます：

相数による分類
- 単相変圧器：単相交流回路で使用される変圧器
- 三相変圧器：三相交流回路で使用される変圧器（三相一体型または単相変圧器の組み合わせ）
冷却方式による分類
- 乾式変圧器：冷却媒体に空気を使用
- 油入変圧器：冷却媒体に絶縁油を使用
- ガス絶縁変圧器：冷却媒体にSF6ガスなどを使用
用途による分類
- 電力用変圧器：発電所、変電所などで使用される大容量変圧器
- 配電用変圧器：配電線路で使用される変圧器
- 計器用変圧器：電圧変成器（PT/VT）や電流変成器（CT）など測定用の変圧器
- 特殊変圧器：整流器用、試験用、調相用など特殊用途の変圧器

イメージ図: 電力用変圧器

イメージ図: 配電用変圧器

イメージ図: 計器用変圧器

分類基準	種類	特徴
相数	単相変圧器	単相回路用、構造が簡単
相数	三相変圧器	三相回路用、鉄心利用率が高い
冷却方式	乾式変圧器	防災性高、内部設置可、中小容量向き
	油入変圧器	冷却・絶縁性能高、大容量向き
	ガス絶縁変圧器	不燃性、環境対応、高価
用途	電力用変圧器	大容量、高効率、長寿命
	配電用変圧器	中小容量、経済性重視
	計器用変圧器	高精度、電圧・電流変換用
	特殊変圧器	整流器用、試験用など特殊用途

2.4 冷却方式

変圧器の運転中には、鉄損や銅損による発熱が生じます。これを効率良く冷却するための方式が採用されています：

乾式変圧器の冷却方式
- 自冷式（AN）：自然対流による空気冷却
- 送風式（AF）：ファンによる強制空冷
油入変圧器の冷却方式
- 油浸自冷式（ONAN）：油の自然対流による冷却
- 油浸風冷式（ONAF）：油の自然対流と放熱器の強制空冷の組み合わせ
- 油浸送油風冷式（OFAF）：油の強制循環と放熱器の強制空冷の組み合わせ
- 油浸送油水冷式（OFWF）：油の強制循環と水冷却器の組み合わせ

冷却方式の選定
変圧器の冷却方式は、容量、設置環境、経済性などを考慮して選定されます。一般的に、小容量の変圧器では自冷式が、大容量になるほど強制冷却方式が採用されます。例えば、配電用変圧器（数百kVA）では油浸自冷式が、大型の電力用変圧器（数百MVA）では油浸送油風冷式や油浸送油水冷式が採用されることが多いです。また、屋内設置の場合には防災性を考慮して乾式変圧器が選ばれる傾向があります。

油入変圧器で使用される絶縁油には、次のような役割があります：

絶縁機能：巻線間や対地間の電気絶縁
冷却機能：発生した熱を放熱器へ運搬
アーク消弧機能：内部で発生するアークの消弧

従来は鉱油（変圧器油）が主に使用されてきましたが、近年は環境や防災性を考慮して、シリコーン油や植物油などの難燃性絶縁油の使用も増えています。

変圧器の基本構造のまとめ

変圧器は主に鉄心と巻線から構成される
鉄心は磁気回路を形成し、珪素鋼板を積層して渦電流損失を低減する
巻線には一次巻線（電源側）と二次巻線（負荷側）があり、材料には主に銅が使用される
変圧器は相数、冷却方式、用途などによって様々な種類に分類される
冷却方式には乾式（空気冷却）と油入式（油冷却）があり、容量や設置環境に応じて選定される
絶縁油は絶縁機能、冷却機能、アーク消弧機能を持つ

3. 変圧器の動作原理

変圧器の動作は、ファラデーの電磁誘導の法則に基づいています。このセクションでは、変圧器の基本的な動作原理と電気的特性について解説します。

3.1 電磁誘導と変圧作用

変圧器の動作原理は、次のようなステップで説明できます：

一次巻線に交流電圧を印加すると、交流電流が流れます
一次巻線の電流によって、鉄心内に交流磁束が発生します
この交流磁束は鉄心を通じて二次巻線を鎖交します
磁束の時間的変化により、二次巻線に電圧が誘起されます（電磁誘導）

ファラデーの電磁誘導の法則によれば、誘導起電力は次の式で与えられます：

\[e = -N\frac{d\phi}{dt}\]

ここで：

\(e\)：誘導起電力 [V]
\(N\)：巻数
\(\frac{d\phi}{dt}\)：磁束の時間変化率 [Wb/s]

磁束が正弦波状に変化する場合（\(\phi = \Phi_m\sin\omega t\)）、誘導起電力の実効値は次のようになります：

\[E = 4.44fN\Phi_m\]

ここで：

\(E\)：誘導起電力の実効値 [V]
\(f\)：周波数 [Hz]
\(N\)：巻数
\(\Phi_m\)：最大磁束 [Wb]

イメージ図: 変圧器の動作原理：磁束を通じて電圧を変換する様子

理想変圧器の条件
理想変圧器とは、以下の条件を満たす変圧器です：

鉄心の磁気抵抗が零（無限大の透磁率）
巻線の抵抗が零
漏れ磁束が零（全磁束が両巻線を鎖交）
鉄損が零
励磁電流が零

実際の変圧器では、これらの条件は完全には満たされませんが、大型の高効率変圧器では理想状態に近づきます。

3.2 電圧・電流関係

変圧器の一次側と二次側の電圧と電流の関係は、巻数比によって決まります：

電圧比：

\[\frac{V_1}{V_2} = \frac{N_1}{N_2} = a\]

電流比（理想変圧器の場合）：

\[\frac{I_1}{I_2} = \frac{N_2}{N_1} = \frac{1}{a}\]

ここで：

\(V_1, V_2\)：一次、二次電圧 [V]
\(I_1, I_2\)：一次、二次電流 [A]
\(N_1, N_2\)：一次、二次巻数
\(a\)：巻数比（変圧比）

理想変圧器では、一次側の入力電力と二次側の出力電力が等しくなります（電力保存則）：

\[V_1 I_1 = V_2 I_2\]

変圧比の計算例
一次電圧6600V、二次電圧210Vの変圧器の巻数比を求めます：

\begin{align*} a = \frac{V_1}{V_2} = \frac{N_1}{N_2} = \frac{6600}{210} = \frac{660}{21} = \frac{220}{7} \approx 31.43 \end{align*}

一次巻線が二次巻線の約31.43倍の巻数を持つことがわかります。

この変圧器で、二次側で30Aの電流が流れている場合、一次側の電流は：

\begin{align*} I_1 = I_2 \times \frac{N_2}{N_1} = 30 \times \frac{1}{31.43} \approx 0.954 \, \mathrm{A} \end{align*}

理想変圧器では、約0.954Aの電流が一次側に流れることになります。

この関係から、次のことがわかります：

昇圧変圧器（\(V_2 > V_1\)）では、二次電流は一次電流より小さくなる
降圧変圧器（\(V_2 < V_1\)）では、二次電流は一次電流より大きくなる

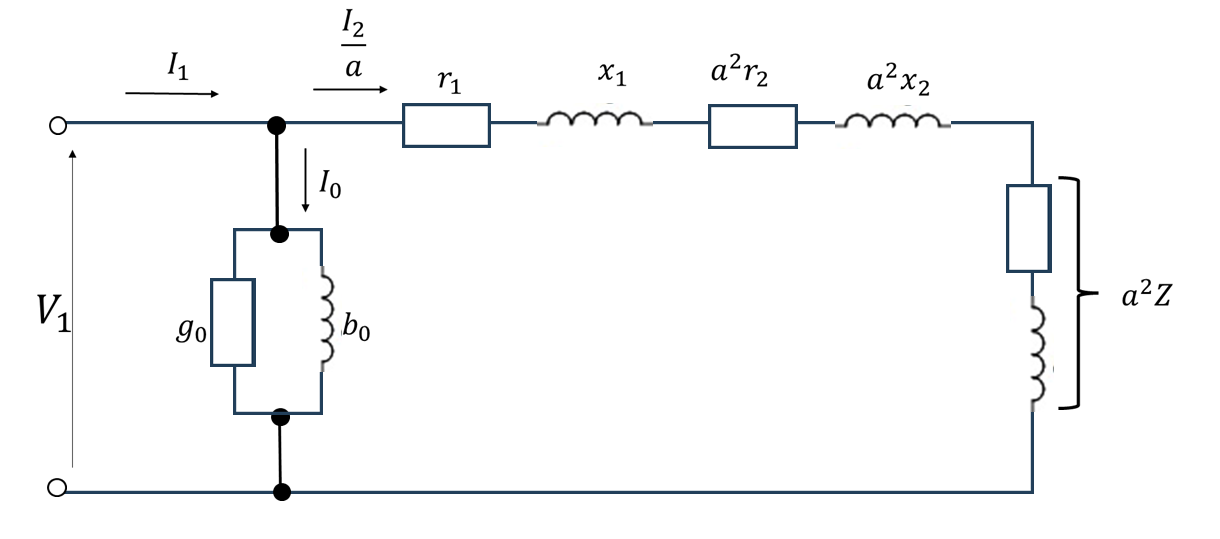
3.3 等価回路

実際の変圧器では、理想的な条件は満たされず、様々な損失や漏れインピーダンスが存在します。これらを考慮した等価回路が用いられます：

変圧器の等価回路では、次の要素が考慮されます：

一次巻線抵抗 \(r_1\)：一次巻線の抵抗
二次巻線抵抗 \(r_2\)：二次巻線の抵抗
一次漏れリアクタンス \(x_1\)：一次巻線の漏れ磁束によるリアクタンス
二次漏れリアクタンス \(x_2\)：二次巻線の漏れ磁束によるリアクタンス
鉄損分路 \(g_0\)：鉄心でのヒステリシス損と渦電流損を表す
励磁リアクタンス \(b_0\)：磁化電流を表す

これらの要素を含む詳細な等価回路は、解析の目的に応じて簡略化されることがあります。よく使われる簡略等価回路には、次のようなものがあります：

T型等価回路の変圧器定数：

一次インピーダンス：\(Z_1 = r_1 + jx_1\)
二次インピーダンス（一次換算）：\(Z_2' = r_2' + jx_2' = a^2(r_2 + jx_2)\)
励磁アドミタンス：\(Y_0 = g_0 - jb_0\)

等価回路の簡略化
変圧器の等価回路は、解析の目的によって次のように簡略化されることがあります：

近似等価回路：励磁回路を省略し、一次側と二次側（一次換算）のインピーダンスを直列接続した回路
さらに簡略化した等価回路：一次と二次のインピーダンスを合成した「漏れインピーダンス」のみを考慮した回路

大型の変圧器では、励磁電流が定格電流の数%程度であり、負荷特性の計算では励磁回路を無視できる場合が多いです。

一次側換算した等価回路

3.4 ベクトル図

変圧器の動作状態を視覚的に理解するために、ベクトル図が用いられます。ベクトル図では、電圧、電流、磁束などの関係を矢印（ベクトル）で表現します。

変圧器のベクトル図は、負荷の力率や巻線の結線方式によって様々な形になります。基本的な単相変圧器のベクトル図の作成手順は次の通りです：

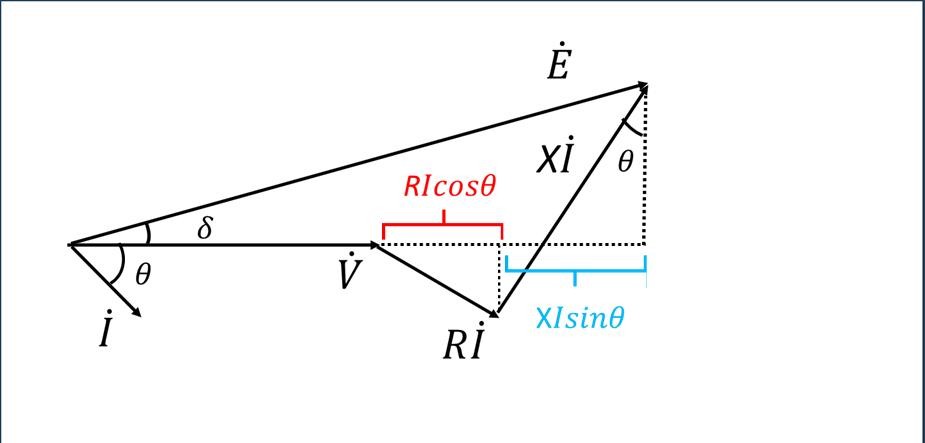
ベクトル図

端子電圧 \(\vec{V}\) をベクトル図の基準として描く
負荷の力率角に応じて、電流 \(\vec{I}\) を描く
回路の電圧降下（\(R\vec{I}\) や \(jX\vec{I}\)）を考慮して、誘導起電力 \(\vec{E}\) を描く
（省略）※図では一次・二次の区別がなく、一本化されているため対応しません
（省略）※励磁電流 \(I_0\) の表記も図には登場しません
（省略）※一次電流 \(I_1\) のベクトル和の描画も図には含まれていません
（省略）※一次側の電圧 \(V_1\) の表示も図には明示されていません

ベクトル図の解釈
添付のベクトル図から、次のような情報を読み取ることができます：

負荷の力率：電流 \(\vec{I}\) と端子電圧 \(\vec{V}\) のなす角 \(\theta\) から判断
電圧降下：抵抗成分 \(R\vec{I}\) とリアクタンス成分 \(jX\vec{I}\) による合成ベクトルから
起電力の位相：起電力 \(\vec{E}\) は、端子電圧 \(\vec{V}\) より進み、角度 \(\delta\) だけずれる
電圧構成：端子電圧 \(\vec{V}\) に電圧降下成分 \(R\vec{I} + jX\vec{I}\) を加えたものが \(\vec{E}\)

例えば、遅れ力率負荷では、電流 \(\vec{I}\) は電圧 \(\vec{V}\) に対して遅れており、リアクタンス成分 \(X\vec{I}\sin\theta\) によって起電力 \(\vec{E}\) はより大きな進み位相を持ちます。
一方、進み力率負荷では、\(\vec{I}\) が \(\vec{V}\) に対して進み、起電力 \(\vec{E}\) の進み角 \(\delta\) は小さくなります。

三相変圧器では、結線方式（Y-Y、Y-Δ、Δ-Y、Δ-Δなど）によってベクトル図が異なります。特に、一次側と二次側で結線方式が異なる場合（Y-ΔやΔ-Y）、線間電圧間に30°の位相差が生じることに注意が必要です。

変圧器の動作原理のまとめ

変圧器は電磁誘導の原理に基づいて動作し、交流電圧を別の交流電圧に変換する
誘導起電力は磁束の時間変化率に比例し、\(E = 4.44fN\Phi_m\) で表される
電圧比は巻数比に等しく、電流比は巻数比の逆数に等しい（理想変圧器の場合）
実際の変圧器では、巻線抵抗、漏れリアクタンス、鉄損、励磁電流などが存在する
これらの要素を考慮した等価回路が、変圧器の特性解析に用いられる
ベクトル図は、変圧器の電圧、電流、磁束などの関係を視覚的に表現する
三相変圧器では、結線方式によって電圧・電流の位相関係が変わる

4. 変圧器の特性

変圧器の性能を理解するためには、その特性を知ることが重要です。このセクションでは、変圧器の無負荷特性、負荷特性、効率、電圧変動率について解説します。

4.1 無負荷特性

無負荷特性とは、二次側が開放された状態（無負荷状態）での変圧器の特性を指します。主な無負荷特性には以下のものがあります：

無負荷電流（励磁電流）：一次側に流れる電流で、主に磁化電流と鉄損電流からなる
無負荷損失（鉄損）：鉄心でのヒステリシス損と渦電流損の合計
変圧比：無負荷時の一次電圧と二次電圧の比

無負荷電流は通常、定格電流の数%程度（大型変圧器では1〜5%、小型変圧器では10〜30%）です。無負荷損失（鉄損）は電圧の二乗に比例し、周波数にも依存します。

鉄損の計算式：

\[P_i = P_h + P_e\]

ここで：

\(P_i\)：鉄損 [W]
\(P_h\)：ヒステリシス損 [W] \(\propto f B_m^{1.6\sim 2}\)
\(P_e\)：渦電流損 [W] \(\propto f^2 B_m^2\)
\(f\)：周波数 [Hz]
\(B_m\)：最大磁束密度 [T]

無負荷電流の成分
無負荷電流（励磁電流）\(I_0\) は、磁化電流 \(I_m\) と鉄損電流 \(I_w\) のベクトル和として表されます：

\[I_0 = \sqrt{I_m^2 + I_w^2}\]

ここで、磁化電流 \(I_m\) は主磁束を発生させるための電流で、電圧より90°遅れます。鉄損電流 \(I_w\) は鉄損による電力損失を補うための電流で、電圧と同相です。一般的に、大型変圧器では \(I_m\) が \(I_w\) より大きく、無負荷力率は0.1〜0.3程度と低くなります。

4.2 負荷特性

負荷特性とは、変圧器に負荷を接続した状態での特性を指します。主な負荷特性には以下のものがあります：

電圧変動特性：負荷電流の変化に対する二次電圧の変動
電流特性：二次電流の変化に対する一次電流の変化
力率特性：負荷力率の変化に対する一次側力率の変化
インピーダンス特性：短絡試験から得られる漏れインピーダンス

負荷特性は、変圧器の等価回路パラメータを用いて解析されます。特に、漏れインピーダンス（抵抗分とリアクタンス分）が負荷特性に大きな影響を与えます。

電圧変動の要因
変圧器の二次電圧が負荷によって変動する主な要因は、以下の2つです：

抵抗降下：巻線抵抗による電圧降下で、負荷電流と力率に依存
リアクタンス降下：漏れリアクタンスによる電圧降下で、負荷電流と力率に依存

力率の影響として、遅れ力率負荷では電圧降下が大きくなり、進み力率負荷では電圧降下が小さくなる（場合によっては電圧上昇となる）ことが挙げられます。

短絡試験（二次側を短絡し、一次側に定格電流が流れる程度の電圧を印加する試験）により、変圧器の等価回路パラメータのうち、漏れインピーダンス成分が測定できます。

4.3 効率と損失

変圧器の効率は、出力電力に対する入力電力の比率で定義されます：

\[\eta = \frac{P_o}{P_i} \times 100\% = \frac{P_o}{P_o + P_{\text{損失}}} \times 100\%\]

ここで：

\(\eta\)：効率 [%]
\(P_o\)：出力電力 [W]
\(P_i\)：入力電力 [W]
\(P_{\text{損失}}\)：全損失 [W]

変圧器の主な損失には、以下のものがあります：

鉄損（無負荷損失） \(P_i\)：鉄心でのヒステリシス損と渦電流損の合計
銅損（負荷損失） \(P_c\)：巻線抵抗による損失（\(I^2R\) 損失）
漂遊負荷損：漏れ磁束による漂遊渦電流損など

鉄損は電圧にほぼ比例し、負荷の大きさにはほとんど依存しません。一方、銅損は負荷電流の二乗に比例します。

銅損の計算式：

\[P_c = I_1^2 r_1 + I_2^2 r_2 \approx I_1^2 (r_1 + r_2')\]

ここで：

\(P_c\)：銅損 [W]
\(I_1, I_2\)：一次、二次電流 [A]
\(r_1, r_2\)：一次、二次巻線抵抗 [Ω]
\(r_2'\)：二次巻線抵抗の一次換算値 [Ω]

最大効率の条件
変圧器の効率は負荷率によって変化し、ある負荷率で最大となります。最大効率となる条件は、鉄損と銅損が等しくなる点です：

\[P_i = P_c\]

この時の負荷率（定格負荷に対する比率）は次式で求められます：

\[x = \sqrt{\frac{P_i}{P_{c,R}}}\]

ここで、\(P_{c,R}\) は定格負荷時の銅損です。大型変圧器では、最大効率となる負荷率は70〜80%程度となります。

実際の変圧器の効率は非常に高く、大型変圧器では99%以上、中型変圧器でも97〜98%程度の効率が達成されています。効率の高さは、変圧器が可動部分を持たない静止器であることの大きな利点の一つです。

4.4 電圧変動率

電圧変動率（または電圧変化率）は、変圧器の負荷特性を表す重要な指標の一つです。これは、定格負荷時と無負荷時の二次電圧の差を定格負荷時の二次電圧で割った値として定義されます：

\[\varepsilon = \frac{V_{2,NL} - V_{2,FL}}{V_{2,FL}} \times 100\%\]

ここで：

\(\varepsilon\)：電圧変動率 [%]
\(V_{2,NL}\)：無負荷時の二次電圧 [V]
\(V_{2,FL}\)：定格負荷時の二次電圧 [V]

電圧変動率は、漏れインピーダンスと負荷の力率によって変化します。等価回路パラメータを用いると、近似的に次式で計算できます：

\[\varepsilon \approx (r \cos\phi + x \sin\phi) \times 100\%\]

ここで：

\(r\)：等価抵抗（パーセント値）
\(x\)：等価リアクタンス（パーセント値）
\(\cos\phi\)：負荷の力率
\(\sin\phi\)：負荷の力率の正弦成分

力率による電圧変動率の変化
電圧変動率は負荷の力率によって大きく変化します：

遅れ力率（誘導性負荷）：電圧変動率が大きくなる（二次電圧が低下）
力率1.0（抵抗性負荷）：電圧変動率は主に抵抗分による
進み力率（容量性負荷）：電圧変動率が小さくなる（場合によっては負になり、二次電圧が上昇）

実際の配電用変圧器では、電圧変動率は3〜5%程度に設計されることが多いです。

変圧器の特性のまとめ

無負荷特性には、無負荷電流（励磁電流）、無負荷損失（鉄損）、変圧比などがある
負荷特性には、電圧変動特性、電流特性、力率特性、インピーダンス特性などがある
変圧器の主な損失は、鉄損（無負荷損）と銅損（負荷損）である
鉄損は電圧に依存し、銅損は電流の二乗に比例する
最大効率となる負荷率は、鉄損と銅損が等しくなる点である
電圧変動率は、無負荷時と全負荷時の二次電圧の変化率として定義される
電圧変動率は負荷の力率に大きく依存し、遅れ力率では大きく、進み力率では小さくなる

5. 変圧器の応用と特殊変圧器

変圧器は様々な用途に応用されており、特殊な目的のために設計された変圧器も多くあります。このセクションでは、配電用変圧器、三相変圧器、特殊変圧器、並行運転について解説します。

5.1 配電用変圧器

配電用変圧器は、電力系統において高電圧の配電線からの電力を、一般需要家が使用できる低電圧に変換する役割を担います。

主な配電用変圧器の特徴：

容量範囲：数kVAから数百kVA程度
電圧比：日本では一般に6.6kV/210V（三相3線式）または6.6kV/105-210V（単相3線式）
冷却方式：油入自冷式または乾式（モールド式など）
設置場所：電柱上（柱上変圧器）、地上（パッド変圧器）、屋内（キュービクルなど）

配電用変圧器では、電圧調整のために次のような機能が設けられることがあります：

タップ切替：一次巻線の巻数を調整して電圧比を変更する機能
負荷時タップ切替装置（LTC）：運転中にタップを切り替えられる装置
自動電圧調整器（AVR）：二次電圧を検出して自動的にタップを調整する装置

柱上変圧器の例
日本の一般的な住宅地域で使用される柱上変圧器は、単相3線式の10〜30kVA程度のものが多いです。この変圧器は、6600Vの高圧配電線から、100/200Vの低圧配電線への変換を行います。構造は、油入自冷式の単相変圧器で、雷サージから保護するためのギャップやアレスターが付属しています。タップ切替は、通常、無電圧時（停電時）に手動で行われます。

5.2 三相変圧器

三相変圧器は、三相交流電力を変換するための変圧器です。三相変圧器には次の2種類があります：

三相一体型変圧器：3つの相が1つの鉄心に収められた構造
単相変圧器バンク：3台の単相変圧器を組み合わせた構造

三相変圧器の結線方式には、次のような基本形式があります：

Y-Y結線：一次、二次ともにY（スター）結線
Δ-Δ結線：一次、二次ともにΔ（デルタ）結線
Y-Δ結線：一次がY結線、二次がΔ結線
Δ-Y結線：一次がΔ結線、二次がY結線

結線方式	特徴	主な用途
Y-Y結線	高電圧に適する、中性点が利用可能、第3次高調波の問題あり	超高圧送電用
Δ-Δ結線	第3次高調波の問題なし、巻線電圧が線間電圧と同じ	中小容量の配電用
Y-Δ結線	降圧用に適する、位相差30°あり、第3次高調波を抑制	降圧用（系統連系など）
Δ-Y結線	昇圧用に適する、位相差30°あり、二次中性点が利用可能	昇圧用（発電所など）

結線方式による位相関係
Y-ΔやΔ-Y結線では、一次側と二次側の線間電圧間に30°の位相差が生じます。これは電力系統の連系において重要な要素です。変圧器の結線を表す際には、「結線記号」が用いられ、例えばYyn0（一次Y結線、二次Y結線、中性点引き出し、位相差0°）のように表記されます。第三種電気主任技術者試験では、この結線記号と位相差の理解が重要です。

三相変圧器での特別な結線方式には、以下のようなものがあります：

スコット結線：三相電力を二相電力に変換する特殊な結線
V結線：2台の単相変圧器で三相変換を行う結線
ジグザグ結線（Z結線）：各相の巻線を2分割して接続する結線で、不平衡負荷や高調波に強い

5.3 特殊変圧器

特定の目的のために設計された特殊変圧器には、次のようなものがあります：

計器用変成器
- 計器用変圧器（PT/VT）：高電圧を測定用の低電圧に変換
- 計器用変流器（CT）：大電流を測定用の小電流に変換
整流器用変圧器：整流回路用の特殊結線や高調波対策が施された変圧器
試験用変圧器：高電圧試験用の特殊な変圧器
電気炉用変圧器：大電流、低電圧用の特殊変圧器
可変変圧器：出力電圧を連続的に調整できる変圧器（スライダック、インダクションレギュレータなど）
単巻変圧器（自己変圧器）：一次と二次が電気的に接続された変圧器

単巻変圧器（自己変圧器）の特徴
単巻変圧器（オートトランス）は、一次と二次が電気的に接続されており、一部の巻線が共用されています。主な特徴は：

同じ定格容量の二巻変圧器と比べて小型・軽量
銅損が少なく、効率が高い
一次と二次が電気的に接続されているため、絶縁レベルに注意が必要
変圧比があまり大きくない場合に経済的

単巻変圧器の実際の巻線容量（通過容量）は、二巻変圧器の等価容量より小さくなります：

\[S_{\text{通過}} = S_{\text{等価}} \times \left(1 - \frac{V_2}{V_1}\right) \quad \text{(昇圧の場合)}\]

例えば、100kVAの等価容量を持つ単巻変圧器で、変圧比が100V:110V（10%昇圧）の場合、実際の巻線容量は100kVA×(1-100/110)=9.1kVAとなります。

計器用変成器は、高電圧・大電流の測定を安全に行うために重要な役割を果たします。計器用変圧器（PT/VT）は電圧を、計器用変流器（CT）は電流を変換します。これらは高い精度が要求され、「変成比誤差」と「位相角誤差」が重要な性能指標となります。

5.4 並行運転

並行運転とは、2台以上の変圧器を並列に接続して負荷を分担させる運転方法です。並行運転により、次のような利点が得られます：

負荷変動に応じた運転台数の調整による効率向上
単一変圧器故障時のバックアップ（信頼性向上）
容量増加時の段階的な設備投資
保守時の連続運転の確保

変圧器を安全に並行運転するための条件（並行条件）は以下の通りです：

一次・二次電圧が等しいこと（変圧比が等しいこと）
極性が一致していること（逆接続されていないこと）
インピーダンス電圧百分率が等しいこと（負荷分担の均等化のため）
三相変圧器の場合は、結線方式と位相が一致していること

並行運転時の負荷分担
並行運転時の各変圧器の負荷分担は、基本的にインピーダンス電圧百分率に反比例します。2台の変圧器の並行運転で、定格容量とインピーダンス電圧百分率がそれぞれ \(S_1\)、\(e_1\) と \(S_2\)、\(e_2\) の場合、負荷電流の分担比は次のようになります：

\[\frac{I_1}{I_2} = \frac{S_1 \times e_2}{S_2 \times e_1}\]

したがって、インピーダンス電圧百分率が等しい場合は、定格容量に比例して負荷が分担されます。

実際の並行運転では、変圧器間の特性差（特にインピーダンス電圧百分率の差）によって、循環電流が生じる場合があります。循環電流は有効電力を消費し、変圧器の温度上昇や効率低下を引き起こすため、できるだけ小さくする必要があります。

並行運転の実例
配電用変電所では、複数の配電用変圧器を並行運転することが一般的です。例えば、3台の20MVA変圧器を設置し、低負荷時は1台または2台を運転、重負荷時は3台全てを運転するといった運用が行われます。これにより、各時間帯での効率的な運転が可能になります。また、1台が故障しても残りの変圧器で運転を継続できる冗長性も確保されます。ただし、並行運転時には保護リレーの協調や遮断器容量の適正化などの検討も必要です。

変圧器の応用と特殊変圧器のまとめ

配電用変圧器は、配電系統で高電圧から低電圧への変換を行う
三相変圧器には三相一体型と単相変圧器バンクがあり、Y結線とΔ結線の組み合わせがある
Y-ΔやΔ-Y結線では、一次と二次の間に30°の位相差が生じる
特殊変圧器には、計器用変成器、整流器用変圧器、試験用変圧器などがある
単巻変圧器（自己変圧器）は、一次と二次が電気的に接続され、小型・高効率が特徴
変圧器の並行運転には、変圧比、極性、インピーダンス電圧などの条件がある
並行運転時の負荷分担は、インピーダンス電圧百分率と定格容量によって決まる

6. 演習問題

6.1 基本計算問題

問題1：変圧比と電流の計算

変圧比が20:1の理想変圧器があり、一次側に200Vの電圧が印加されている。二次側に5Ωの抵抗負荷が接続されているとき、(a) 二次電圧、(b) 二次電流、(c) 一次電流を求めよ。

解答：

(a) 二次電圧の計算：

変圧比が20:1なので、二次電圧は次のように求められます：

\begin{align*} \frac{V_1}{V_2} &= \frac{N_1}{N_2} = 20:1 \\[10pt] V_2 &= \frac{V_1}{20} \\[10pt] &= \frac{200}{20} \\[10pt] &= 10 \, \mathrm{V} \end{align*}

(b) 二次電流の計算：

二次側に5Ωの抵抗負荷が接続されているので、二次電流は次のように求められます：

\begin{align*} I_2 &= \frac{V_2}{R_2} \\[10pt] &= \frac{10}{5} \\[10pt] &= 2 \, \mathrm{A} \end{align*}

(c) 一次電流の計算：

理想変圧器では、次の関係が成り立ちます：

\begin{align*} \frac{I_1}{I_2} &= \frac{N_2}{N_1} = \frac{1}{20} \\[10pt] I_1 &= I_2 \times \frac{N_2}{N_1} \\[10pt] &= 2 \times \frac{1}{20} \\[10pt] &= 0.1 \, \mathrm{A} \end{align*}

したがって、二次電圧は10V、二次電流は2A、一次電流は0.1Aです。

確認のため、一次側と二次側の電力を計算してみます：

\begin{align*} P_1 &= V_1 \times I_1 = 200 \times 0.1 = 20 \, \mathrm{W} \\ P_2 &= V_2 \times I_2 = 10 \times 2 = 20 \, \mathrm{W} \end{align*}

両者が等しいことから、理想変圧器の電力保存則が満たされていることが確認できます。

問題2：変圧器の効率と損失

定格容量100kVA、定格電圧6600V/210Vの変圧器がある。無負荷試験では、一次側に6600Vを印加したとき、一次電流は0.5A、入力電力は900Wであった。また、短絡試験では、一次側に400Vを印加したとき、一次電流は15.2A、入力電力は1600Wであった。この変圧器の全負荷時の効率と力率0.8の75%負荷時の効率を求めよ。

解答：

(1) まず、無負荷試験から鉄損（無負荷損失）を求めます：

\[P_i = 900 \, \mathrm{W}\]

(2) 次に、短絡試験から銅損（負荷損失）を求めます。短絡試験では定格電流の状態で測定するため、実際の定格電流に対する補正が必要です：

定格電流は：

\[I_{1,R} = \frac{S_R}{V_1} = \frac{100 \times 10^3}{6600} = 15.15 \, \mathrm{A}\]

短絡試験での測定電流は15.2Aなので、ほぼ定格電流と見なせます。よって、定格負荷時の銅損は：

\[P_c = 1600 \, \mathrm{W}\]

(3) 全負荷時（定格負荷時）の効率を計算します：

\begin{align*} \eta_{FL} &= \frac{P_o}{P_o + P_i + P_c} \times 100\% \\[10pt] &= \frac{S_R \times \cos\phi}{S_R \times \cos\phi + P_i + P_c} \times 100\% \end{align*}

ここで、力率が指定されていないため、一般的な変圧器の定格力率である0.8と仮定します：

\begin{align*} \eta_{FL} &= \frac{100 \times 10^3 \times 0.8}{100 \times 10^3 \times 0.8 + 900 + 1600} \times 100\% \\[10pt] &= \frac{80000}{80000 + 900 + 1600} \times 100\% \\[10pt] &= \frac{80000}{82500} \times 100\% \\[10pt] &= 97.0\% \end{align*}

(4) 力率0.8の75%負荷時の効率を計算します。75%負荷時の銅損は負荷率の二乗に比例するので：

\[P_{c,75\%} = P_c \times (0.75)^2 = 1600 \times 0.5625 = 900 \, \mathrm{W}\]

よって、75%負荷時の効率は：

\begin{align*} \eta_{75\%} &= \frac{S_R \times 0.75 \times \cos\phi}{S_R \times 0.75 \times \cos\phi + P_i + P_{c,75\%}} \times 100\% \\[10pt] &= \frac{100 \times 10^3 \times 0.75 \times 0.8}{100 \times 10^3 \times 0.75 \times 0.8 + 900 + 900} \times 100\% \\[10pt] &= \frac{60000}{60000 + 900 + 900} \times 100\% \\[10pt] &= \frac{60000}{61800} \times 100\% \\[10pt] &= 97.1\% \end{align*}

したがって、全負荷時の効率は97.0%、力率0.8の75%負荷時の効率は97.1%となります。この結果から、この変圧器は75%負荷時にわずかに効率が高くなっていることがわかります。これは、負荷率が下がると銅損が減少するためですが、あまりに低負荷になると今度は全損失に対する鉄損の割合が大きくなり、効率が下がることになります。

問題3：変圧器の電圧変動率

ある変圧器の等価抵抗が1.2%、等価リアクタンスが4.8%である。この変圧器に力率0.8（遅れ）の負荷を接続した場合の電圧変動率を求めよ。また、力率1.0および力率0.8（進み）の場合の電圧変動率も求めよ。

解答：

変圧器の電圧変動率は、近似的に次の式で計算できます：

\[\varepsilon \approx (r \cos\phi + x \sin\phi) \times 100\%\]

ここで：

\(r\)：等価抵抗（パーセント値）= 1.2%
\(x\)：等価リアクタンス（パーセント値）= 4.8%
\(\cos\phi\)：負荷の力率
\(\sin\phi\)：負荷の力率の正弦成分

(1) 力率0.8（遅れ）の場合：

\(\cos\phi = 0.8\)（遅れ）であるため、\(\sin\phi = \sqrt{1-\cos^2\phi} = \sqrt{1-0.8^2} = 0.6\)（正の値）となります。

\begin{align*} \varepsilon &\approx (r \cos\phi + x \sin\phi) \times 100\% \\[10pt] &= (0.012 \times 0.8 + 0.048 \times 0.6) \times 100\% \\[10pt] &= (0.0096 + 0.0288) \times 100\% \\[10pt] &= 0.0384 \times 100\% \\[10pt] &= 3.84\% \end{align*}

(2) 力率1.0の場合：

\(\cos\phi = 1.0\)であるため、\(\sin\phi = 0\)となります。

\begin{align*} \varepsilon &\approx (r \cos\phi + x \sin\phi) \times 100\% \\[10pt] &= (0.012 \times 1.0 + 0.048 \times 0) \times 100\% \\[10pt] &= 0.012 \times 100\% \\[10pt] &= 1.2\% \end{align*}

(3) 力率0.8（進み）の場合：

\(\cos\phi = 0.8\)（進み）であるため、\(\sin\phi = -\sqrt{1-\cos^2\phi} = -\sqrt{1-0.8^2} = -0.6\)（負の値）となります。進み力率では、電流は電圧より位相が進むので、\(\sin\phi\) は負の値になります。

\begin{align*} \varepsilon &\approx (r \cos\phi + x \sin\phi) \times 100\% \\[10pt] &= (0.012 \times 0.8 + 0.048 \times (-0.6)) \times 100\% \\[10pt] &= (0.0096 - 0.0288) \times 100\% \\[10pt] &= -0.0192 \times 100\% \\[10pt] &= -1.92\% \end{align*}

したがって、力率0.8（遅れ）の場合の電圧変動率は3.84%、力率1.0の場合は1.2%、力率0.8（進み）の場合は-1.92%となります。

電圧変動率が負の値になるということは、負荷を接続すると無負荷時より電圧が上昇することを意味します。これは、進み力率負荷の特性で、リアクタンス降下が電圧降下ではなく電圧上昇として作用するためです。

6.2 過去問題

問題4：変圧器の特性計算（第三種電気主任技術者試験類似問題）

定格容量1500kVA、定格電圧6600V/440Vの三相変圧器がある。無負荷試験では一次側に定格電圧を印加したときの損失が8kW、短絡試験では二次側を短絡し、一次側に480Vを印加したときの損失が15kWであった。この変圧器の力率0.9で運転した場合の75%負荷時の効率を求めよ。

解答：

(1) まず、無負荷試験から鉄損（無負荷損失）を求めます：

\[P_i = 8 \, \mathrm{kW}\]

(2) 次に、短絡試験から定格負荷時の銅損（負荷損失）を求めます。短絡試験は480Vで行われていますが、定格電圧は6600Vです。銅損は電圧の二乗に比例するため、定格負荷時の銅損は次のように計算されます：

\begin{align*} P_c &= P_{\text{短絡}} \times \left(\frac{V_{\text{定格}}}{V_{\text{短絡}}}\right)^2 \\[10pt] &= 15 \times \left(\frac{6600}{480}\right)^2 \\[10pt] &= 15 \times \left(\frac{6600}{480}\right)^2 \\[10pt] \end{align*}

ここで計算の誤りがあります。短絡試験では一次側に低い電圧を印加して定格電流を流すため、電圧比で補正する必要はありません。したがって、短絡試験で得られた損失15kWが定格負荷時の銅損となります：

\[P_c = 15 \, \mathrm{kW}\]

(3) 75%負荷時の銅損は、負荷率の二乗に比例するので：

\[P_{c,75\%} = P_c \times (0.75)^2 = 15 \times 0.5625 = 8.44 \, \mathrm{kW}\]

(4) 力率0.9で運転した場合の75%負荷時の効率を計算します：

\begin{align*} \eta_{75\%} &= \frac{S_R \times 0.75 \times \cos\phi}{S_R \times 0.75 \times \cos\phi + P_i + P_{c,75\%}} \times 100\% \\[10pt] &= \frac{1500 \times 0.75 \times 0.9}{1500 \times 0.75 \times 0.9 + 8 + 8.44} \times 100\% \\[10pt] &= \frac{1012.5}{1012.5 + 8 + 8.44} \times 100\% \\[10pt] &= \frac{1012.5}{1028.94} \times 100\% \\[10pt] &= 98.4\% \end{align*}

したがって、この変圧器の力率0.9で運転した場合の75%負荷時の効率は98.4%となります。

問題5：変圧器の並行運転（第三種電気主任技術者試験類似問題）

100kVA（インピーダンス電圧4%）と200kVA（インピーダンス電圧5%）の2台の変圧器を並行運転し、合計250kVAの負荷に給電している。各変圧器の負荷分担を求めよ。

解答：

並行運転時の各変圧器の負荷分担は、基本的にインピーダンス電圧百分率に反比例し、定格容量に比例します。2台の変圧器の負荷分担比は次の式で計算できます：

\[\frac{S_1}{S_2} = \frac{S_{R1} \times e_2}{S_{R2} \times e_1}\]

ここで：

\(S_1, S_2\)：各変圧器の負荷分担 [kVA]
\(S_{R1}, S_{R2}\)：各変圧器の定格容量 [kVA]
\(e_1, e_2\)：各変圧器のインピーダンス電圧 [%]

変圧器1（100kVA, 4%）と変圧器2（200kVA, 5%）の負荷分担比は：

\begin{align*} \frac{S_1}{S_2} &= \frac{S_{R1} \times e_2}{S_{R2} \times e_1} \\[10pt] &= \frac{100 \times 5}{200 \times 4} \\[10pt] &= \frac{500}{800} \\[10pt] &= \frac{5}{8} \end{align*}

合計負荷が250kVAなので、次の方程式を解きます：

\[S_1 + S_2 = 250\] \[\frac{S_1}{S_2} = \frac{5}{8}\]

2つ目の式から：

\[S_1 = \frac{5}{8} \times S_2\]

これを1つ目の式に代入すると：

\begin{align*} \frac{5}{8} \times S_2 + S_2 &= 250 \\[10pt] \frac{5 + 8}{8} \times S_2 &= 250 \\[10pt] \frac{13}{8} \times S_2 &= 250 \\[10pt] S_2 &= 250 \times \frac{8}{13} \\[10pt] &= 2000 \times \frac{1}{13} \\[10pt] &= 153.8 \, \mathrm{kVA} \end{align*}

よって、\(S_1\) は：

\begin{align*} S_1 &= 250 - S_2 \\[10pt] &= 250 - 153.8 \\[10pt] &= 96.2 \, \mathrm{kVA} \end{align*}

あるいは、\(S_1 = \frac{5}{8} \times S_2 = \frac{5}{8} \times 153.8 = 96.1 \, \mathrm{kVA}\) としても同じ結果が得られます（端数の処理による微小な差異はあります）。

したがって、100kVAの変圧器は約96.2kVA（負荷率約96.2%）、200kVAの変圧器は約153.8kVA（負荷率約76.9%）の負荷を分担します。

確認のため、計算した負荷分担比を求めてみると：

\[\frac{S_1}{S_2} = \frac{96.2}{153.8} \approx \frac{5}{8}\]

という関係が成り立っています。

演習問題のポイント

変圧器の基本式（変圧比、電流比など）を正確に理解し使用すること
効率計算では、鉄損が電圧に、銅損が電流の二乗に比例することを考慮すること
電圧変動率の計算では、負荷の力率（特に遅れか進みか）に注意すること
同じ条件下での負荷率による効率の変化を理解すること
並行運転時の負荷分担は、インピーダンス電圧と定格容量の関係で決まることを理解すること
単位の一貫性に注意すること（特にkVAとVA、kWとWの変換など）

【第三種電気主任技術者試験】変圧器の完全解説 - 構造から特性・応用まで

目次

1. イントロダクション

2. 変圧器の基本構造

2.1 鉄心の構造

2.2 巻線の構造

2.3 変圧器の種類

2.4 冷却方式

3. 変圧器の動作原理

3.1 電磁誘導と変圧作用

3.2 電圧・電流関係

3.3 等価回路

3.4 ベクトル図

4. 変圧器の特性

4.1 無負荷特性

4.2 負荷特性

4.3 効率と損失

4.4 電圧変動率

5. 変圧器の応用と特殊変圧器

5.1 配電用変圧器

5.2 三相変圧器

5.3 特殊変圧器

5.4 並行運転

6. 演習問題

6.1 基本計算問題

6.2 過去問題

まとめ