【機械】令和1年 問8|並列運転する単相変圧器間の循環電流の計算問題
\( 2 \) 台の単相変圧器があり,それぞれ,巻数比(一次巻数 / 二次巻数)が \( 30.1 \),\( 30.0 \),二次側に換算した巻線抵抗および漏れリアクタンスからなるインピーダンスが \( \left( 0.013 + \mathrm{j}0.022 \right) \) [\( \Omega \)],\( \left( 0.010 + \mathrm{j}0.020 \right) \) [\( \Omega \)] である。
この \( 2 \) 台の変圧器を並列接続し二次側を無負荷として,一次側に \( 6600 \) [V] を加えた。
この \( 2 \) 台の変圧器の二次巻線間を循環して流れる電流の値 [\( \mathrm{A} \)] として,最も近いものを次の (1)~(5) のうちから一つ選べ。
ただし,励磁回路のアドミタンスの影響は無視するものとする。
合格への方程式
変圧器の巻数比の基本原理
変圧器は電磁誘導の原理を利用して、交流電圧を別の交流電圧に変換する静止器です。その中心となる概念が巻数比です。
変圧器の巻数比の定義
変圧器の一次側の巻数を \(N_1\)、二次側の巻数を \(N_2\) とすると、変圧器の巻数比 \(a\) は次式で定義されます:
\[ \begin{aligned} a &= \frac{N_1}{N_2} \\[10pt] \end{aligned} \]
巻数比は変圧器の最も基本的な特性であり、一次側と二次側のコイルの巻き数の比率を表します。この比率によって、電圧と電流の変換率が決まります。
巻数比の物理的意味
巻数比は電磁誘導において、一次側と二次側の電圧・電流の変換比率を決定します。これはファラデーの電磁誘導の法則に基づいています。コイルに流れる電流が作る磁束の変化が、コイルの巻数に比例した起電力を発生させるというものです。
変圧器の動作原理を理解するには、まず交流電源が一次側コイルに接続されると、交流電流が流れ、鉄心に交流磁束が発生します。この交流磁束が二次側コイルを貫くと、電磁誘導によって二次側コイルに起電力が発生します。
理想変圧器の条件
・鉄損(ヒステリシス損・渦電流損)がない
・銅損(巻線抵抗による損失)がない
・漏れ磁束がない(結合係数=1)
・励磁電流が無視できる
理想変圧器においては、一次側と二次側の巻数比が電圧比と電流比を完全に決定します。実際の変圧器では様々な損失や漏れ磁束があるため、理想的な関係からは若干ずれますが、基本原理は同じです。
変圧器の電圧・電流特性
理想変圧器においては、巻数比 \(a\) に基づいて電圧と電流の関係が明確に定義されます。
電圧と電流の基本関係式
巻数比 \(a\) を用いると、一次電圧 \(V_1\)、二次電圧 \(V_2\)、一次電流 \(I_1\)、二次電流 \(I_2\) の間には以下の関係があります:
\[ \begin{aligned} a &= \frac{V_1}{V_2} = \frac{I_2}{I_1} \\[10pt] \end{aligned} \]
関係式の物理的解釈
・電圧比:一次側の巻数が二次側より多い場合(\(a > 1\))、電圧は降下します(降圧変圧器)
・電圧比:一次側の巻数が二次側より少ない場合(\(a < 1\))、電圧は上昇します(昇圧変圧器)
・電流比:電圧とは逆の関係となり、降圧変圧器では二次電流が増加し、昇圧変圧器では二次電流が減少します
例:巻数比と電圧・電流の関係
巻数比 \(a = 5\) の変圧器があり、一次電圧が \(V_1 = 6600 \; [\mathrm{V}]\) のとき:
二次電圧 \(V_2\) は:
\[ \begin{aligned} V_2 &= \frac{V_1}{a} \\[10pt] &= \frac{6600}{5} \\[10pt] &= 1320 \; [\mathrm{V}] \end{aligned} \]
また、二次電流 \(I_2 = 10 \; [\mathrm{A}]\) のとき、一次電流 \(I_1\) は:
\[ \begin{aligned} I_1 &= \frac{I_2}{a} \\[10pt] &= \frac{10}{5} \\[10pt] &= 2 \; [\mathrm{A}] \end{aligned} \]
実際の変圧器での注意点
実際の変圧器では、無負荷時にも励磁電流が流れるため、完全に \(I_1 = I_2/a\) とはなりません。また、巻線抵抗や漏れインダクタンスの影響で、電圧比も理想値から若干ずれることがあります。
変圧器の電圧・電流特性は、電力系統において電圧を変換し、電力を効率的に送電するために極めて重要です。特に長距離送電では、高電圧・低電流で送電し、利用地点で低電圧・高電流に変換することで、送電損失を最小限に抑えています。
変圧器の等価回路と応用
実際の変圧器を解析するためには、等価回路を用いることで様々な特性を理解することができます。
変圧器のT形等価回路
実際の変圧器は以下のパラメータを含む等価回路で表現できます:
\(\dot{V}_1 \; [\mathrm{V}]\):一次側端子電圧
\(I_1 \; [\mathrm{A}]\):一次電流
\(I_2 \; [\mathrm{A}]\):二次電流
\(I_0 \; [\mathrm{A}]\):励磁電流
\(r_1 \; [\Omega]\):一次巻線抵抗
\(r_2 \; [\Omega]\):二次巻線抵抗(一次換算値)
\(x_1 \; [\Omega]\):一次漏れリアクタンス
\(x_2 \; [\Omega]\):二次漏れリアクタンス(一次換算値)
\(a = \frac{N_1}{N_2}\):変圧比
二次側インピーダンスの一次側への換算
二次側のインピーダンス \(Z_2\) を一次側に換算した値 \(Z_2'\) は、巻数比の二乗を用いて:
\[ \begin{aligned} Z_2' &= a^2 \cdot Z_2 \\[10pt] \end{aligned} \]
変圧器の一次換算等価回路
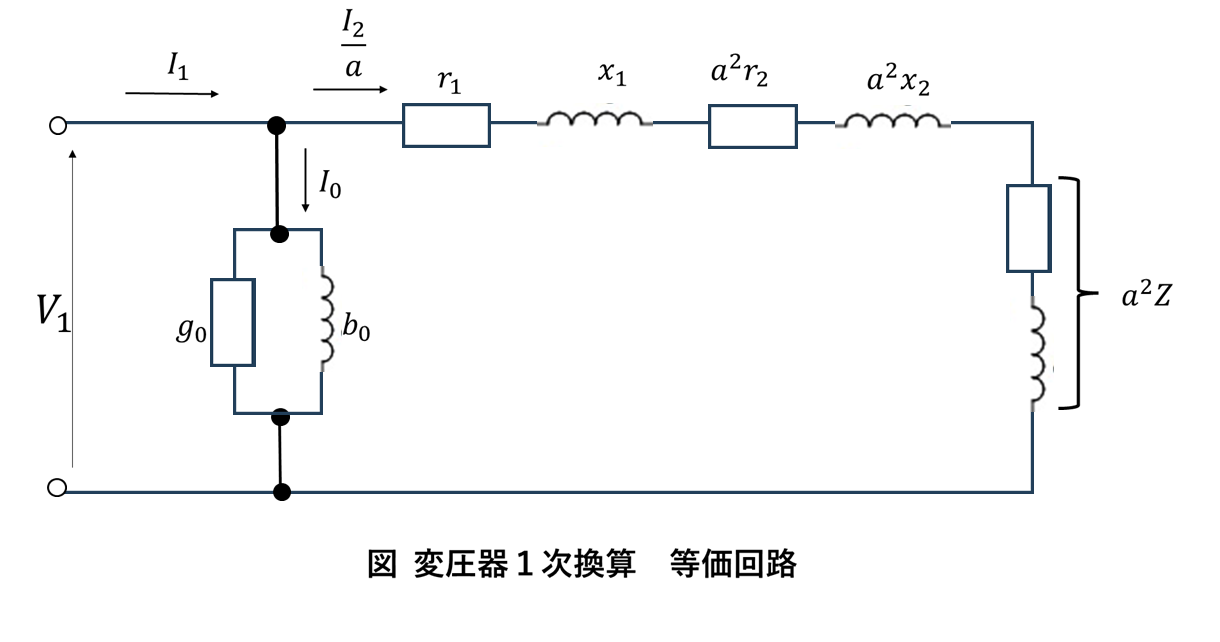
等価回路を用いることで、負荷時の電圧降下や効率、力率などの様々な特性を計算できます。実際の解析では、励磁回路と漏れインピーダンスを考慮した等価回路が用いられます。
変圧器応用の基本原理
変圧器は以下のような多くの応用があります:
1. 電圧変換:送電系統での電圧レベルの変換(発電所→送電線→変電所→配電線→需要家)
2. 絶縁分離:異なる電気系統間の電気的絶縁を提供
3. インピーダンス整合:電源と負荷間のインピーダンス整合を実現
4. 計測用:電流変成器(CT)や電圧変成器(PT/VT)として高電圧・大電流の測定に使用
等価回路使用時の注意点
等価回路パラメータは周波数依存性があるため、定格周波数(50Hz/60Hz)以外での使用時には注意が必要です。また、飽和現象などの非線形特性は等価回路では表現できない場合があります。
変圧器の計算例題
例題1: 巻数比と電圧・電流計算
一次巻数 \(N_1 = 1000\) 回、二次巻数 \(N_2 = 200\) 回の変圧器があります。一次電圧 \(V_1 = 6000 \; [\mathrm{V}]\) のとき、次の値を求めなさい。
(1) 巻数比 \(a\)
(2) 二次電圧 \(V_2\)
(3) 二次電流 \(I_2\) が \(25 \; [\mathrm{A}]\) のときの一次電流 \(I_1\)
解答:
(1) 巻数比 \(a\)
\[ \begin{aligned} a &= \frac{N_1}{N_2} \\[10pt] &= \frac{1000}{200} \\[10pt] &= 5 \end{aligned} \]
(2) 二次電圧 \(V_2\)
\[ \begin{aligned} V_2 &= \frac{V_1}{a} \\[10pt] &= \frac{6000}{5} \\[10pt] &= 1200 \; [\mathrm{V}] \end{aligned} \]
(3) 一次電流 \(I_1\)
\[ \begin{aligned} I_1 &= \frac{I_2}{a} \\[10pt] &= \frac{25}{5} \\[10pt] &= 5 \; [\mathrm{A}] \end{aligned} \]
例題2: 変圧器の電力計算
巻数比 \(a = 10\) の理想変圧器があります。二次側に \(100 \; [\Omega]\) の抵抗負荷が接続されており、一次電圧が \(2200 \; [\mathrm{V}]\) のとき、次の値を求めなさい。
(1) 二次電圧 \(V_2\)
(2) 二次電流 \(I_2\)
(3) 一次電流 \(I_1\)
(4) 負荷で消費される電力 \(P\)
解答:
(1) 二次電圧 \(V_2\)
\[ \begin{aligned} V_2 &= \frac{V_1}{a} \\[10pt] &= \frac{2200}{10} \\[10pt] &= 220 \; [\mathrm{V}] \end{aligned} \]
(2) 二次電流 \(I_2\)
\[ \begin{aligned} I_2 &= \frac{V_2}{R} \\[10pt] &= \frac{220}{100} \\[10pt] &= 2.2 \; [\mathrm{A}] \end{aligned} \]
(3) 一次電流 \(I_1\)
\[ \begin{aligned} I_1 &= \frac{I_2}{a} \\[10pt] &= \frac{2.2}{10} \\[10pt] &= 0.22 \; [\mathrm{A}] \end{aligned} \]
(4) 負荷電力 \(P\)
\[ \begin{aligned} P &= V_2 \cdot I_2 \\[10pt] &= 220 \cdot 2.2 \\[10pt] &= 484 \; [\mathrm{W}] \end{aligned} \]
計算のポイント
・理想変圧器の計算では、一次側と二次側の見かけの電力(電圧×電流)は等しくなります
・実際の変圧器では損失があるため、一次側電力>二次側電力となります
・巻数比は電圧変換と電流変換の両方に影響します
変圧器の損失と効率
実際の変圧器では、理想的な巻数比による変換だけでなく、様々な損失が発生します。これらの損失を理解することは、変圧器の効率や熱設計において重要です。
変圧器の主な損失
1. 鉄損(鉄心損失):
・ヒステリシス損:鉄心の磁化曲線のヒステリシスによる損失
・渦電流損:鉄心内に誘導される渦電流による損失
2. 銅損(巻線損失):
・巻線の抵抗による \(I^2R\) 損失
・一次銅損:\(P_{cu1} = I_1^2 \cdot r_1 \; [\mathrm{W}]\)
・二次銅損:\(P_{cu2} = I_2^2 \cdot r_2 \; [\mathrm{W}]\)
3. 漂遊損失:
・漏れ磁束による金属部分での渦電流損失
損失と負荷の関係
・鉄損:負荷に関係なくほぼ一定(電圧に依存)
・銅損:負荷電流の二乗に比例して増加
変圧器の効率 \(\eta\) は、出力電力を入力電力で割った値で、以下の式で計算できます:
\[ \begin{aligned} \eta &= \frac{P_{out}}{P_{in}} \times 100 \; [\%] \\[10pt] &= \frac{P_{in} - P_{loss}}{P_{in}} \times 100 \; [\%] \\[10pt] &= \left(1 - \frac{P_{loss}}{P_{in}}\right) \times 100 \; [\%] \end{aligned} \]
ここで、\(P_{loss}\) は全損失(鉄損+銅損+その他の損失)です。
最大効率の条件
変圧器の効率が最大になるのは、銅損と鉄損が等しくなる負荷条件のときです:
\[ \begin{aligned} P_{cu} &= P_{i} \\[10pt] \end{aligned} \]
ここで、\(P_{cu}\) は銅損、\(P_{i}\) は鉄損です。
効率向上のための工夫
・鉄損低減:高品質の珪素鋼板の使用、薄い鋼板の積層
・銅損低減:低抵抗の銅線使用、巻線断面積の最適化
・冷却方式の改善:油入、強制風冷、水冷などによる放熱性向上
変圧器の効率は通常97%~99%程度と非常に高く、電力変換器の中では最も効率の高い機器の一つです。特に大容量変圧器ほど効率が高くなる傾向があります。
🔍 ワンポイントアドバイス: 変圧器の巻数比は電気主任技術者試験でよく出題されます。巻数比 \(a\) を覚えるときは「一次側から二次側へ」の変換という方向性をイメージすると記憶しやすいでしょう。また、電圧比と電流比は逆数関係であることもポイントです。実際の計算では、\(a > 1\) なら降圧・二次電流増加、\(a < 1\) なら昇圧・二次電流減少と覚えておくと便利です。
今日は変圧器の並列運転における循環電流について学ぶで!まずはこの問題の状況を整理しよか。
巻数比が少し異なる二つの変圧器を並列接続したときに、循環電流がどれくらい流れるかを計算する問題や。具体的には、巻数比\(a_1 = 30.1\)の変圧器1と巻数比\(a_2 = 30.0\)の変圧器2が並列に接続されているんや。
まずは、それぞれの変圧器の二次側電圧を計算してみよか。変圧器の一次側電圧は\(6600\,\mathrm{[V]}\)やけど、二次側電圧はどうなるかな?
はい、先生!変圧器の一次側と二次側の電圧比は巻数比に反比例しますので、二次側電圧は次のように計算できます:
変圧器1(巻数比\(a_1 = 30.1\))の二次側電圧\(V_1\):
\[ \begin{aligned} V_1 &= \frac{6600}{a_1} \\[10pt] &= \frac{6600}{30.1} \\[10pt] &\approx 219.269\,\mathrm{[V]} \end{aligned} \]変圧器2(巻数比\(a_2 = 30.0\))の二次側電圧\(V_2\):
\[ \begin{aligned} V_2 &= \frac{6600}{a_2} \\[10pt] &= \frac{6600}{30.0} \\[10pt] &= 220\,\mathrm{[V]} \end{aligned} \]ええ計算や!二つの変圧器の二次側電圧には少し差があるね。変圧器1の二次側電圧は約\(219.269\,\mathrm{[V]}\)で、変圧器2の二次側電圧は\(220\,\mathrm{[V]}\)や。
この電圧差があるから循環電流が流れるんやけど、循環電流はどう求めたらええと思う?二つの変圧器のインピーダンスも考慮せなあかんで。変圧器1のインピーダンスは\(Z_1 = 0.013 + \mathrm{j}0.022\,\mathrm{[\Omega]}\)、変圧器2のインピーダンスは\(Z_2 = 0.010 + \mathrm{j}0.020\,\mathrm{[\Omega]}\)や。
循環電流\(I\)は、二つの変圧器間の電位差を両方の変圧器のインピーダンスの和で割ることで求められます。オームの法則を適用すると:
→ 横スクロールして下さい →
\[ \begin{aligned} I &= \frac{V_2 - V_1}{Z_1 + Z_2} \\[10pt] &= \frac{220 - 219.269}{(0.013 + \mathrm{j}0.022) + (0.010 + \mathrm{j}0.020)} \\[10pt] &= \frac{0.731}{0.023 + \mathrm{j}0.042}\,\mathrm{[A]} \end{aligned} \]ここで、分子は電圧の差で実数ですが、分母はインピーダンスの和で複素数となっています。
そうやな!循環電流は電圧差をインピーダンスの和で割ったものや。分子は\(0.731\,\mathrm{[V]}\)で、分母は\(0.023 + \mathrm{j}0.042\,\mathrm{[\Omega]}\)やね。
ここで、循環電流の大きさ\(|I|\)を求めるには、どうしたらええかな?複素数の分母を処理する方法を考えてみ。
循環電流の大きさ\(|I|\)を求めるには、複素数の絶対値を計算します。複素数\(z = a + \mathrm{j}b\)の絶対値は\(|z| = \sqrt{a^2 + b^2}\)で求められます。
つまり、分母の絶対値を計算します:
→ 横スクロールして下さい →
\[ \begin{aligned} |0.023 + \mathrm{j}0.042| &= \sqrt{0.023^2 + 0.042^2} \\[10pt] &= \sqrt{0.000529 + 0.001764} \\[10pt] &= \sqrt{0.002293} \\[10pt] &\approx 0.04789 \end{aligned} \]ええ計算やな!複素数のインピーダンスの絶対値をきちんと求められたね。分母の絶対値が\(|0.023 + \mathrm{j}0.042| \approx 0.04789\)やから、次は循環電流の大きさ\(|I|\)を求めよか。
循環電流\(I\)は\(\frac{0.731}{0.023 + \mathrm{j}0.042}\)やから、その大きさ\(|I|\)はどうなるかな?
はい!循環電流の大きさ\(|I|\)は、分子の絶対値を分母の絶対値で割ることで求められます:
\[ \begin{aligned} |I| &= \left|\frac{0.731}{0.023 + \mathrm{j}0.042}\right| \\[10pt] &= \frac{|0.731|}{|0.023 + \mathrm{j}0.042|} \\[10pt] &= \frac{0.731}{0.04789} \\[10pt] &\approx 15.26\,\mathrm{[A]} \end{aligned} \]よく計算できてるな!\(|I| \approx 15.26\,\mathrm{[A]}\)やね。ここで有効数字について考えよか。元の問題の数値の精度を考えると、最終的な答えはどうなるやろか?
有効数字を考慮すると、元の計算で使用した値(特にインピーダンス値)は小数点第3位までの精度です。したがって、最終結果も同程度の精度にすべきです。
15.26は小数点第2位までとし、四捨五入すると:
\[ |I| \approx 15.3\,\mathrm{[A]} \]よって、
選択肢の(3)が答えです。
素晴らしい計算や!複素数の扱いもよくわかってるな。
循環電流の大きさは\(|I| \approx 15.3\,\mathrm{[A]}\)と求められたな。これが答えや。わずかな巻数比の違い(\(30.1\)と\(30.0\))で、これだけの循環電流が流れるんやね。
実際の変圧器の並列運転では、この循環電流をできるだけ小さくすることが大事や。巻数比だけじゃなく、インピーダンスの大きさや位相角も合わせる必要があるんや。
今回の計算でわかるように、わずかな違いでも結構大きな循環電流が流れるから注意が必要やね。
はい、先生!今回の計算で、わずかな巻数比の差(30.1と30.0)でも、かなりの大きさの循環電流(15.3 A)が流れることがわかりました。
変圧器の並列運転において重要なポイントを学ぶことができました:
1. 変圧器の二次側電圧は巻数比に反比例する (\(V_{\mathrm{sec}} = \frac{V_{\mathrm{pri}}}{a}\))
2. 並列接続された変圧器間に電圧差があると循環電流が流れる
3. 循環電流は電圧差をインピーダンスの和で割ったもの (\(I = \frac{V_2 - V_1}{Z_1 + Z_2}\))
4. 複素インピーダンスがある場合、電流の大きさは複素数の絶対値を使って計算する
5. 実際の並列運転では、巻数比だけでなくインピーダンスの整合も重要
この循環電流は無駄な電力損失を引き起こし、変圧器の定格電流を超えると過熱の原因にもなりますね。
解説まとめ
■ 並列接続変圧器の循環電流とは
変圧器を並列に接続する場合、巻数比にわずかな差があると、二次側に電圧差が生じ、これによって循環電流が流れます。この循環電流は負荷電流とは別に変圧器間を流れるため、変圧器の損失増加や過熱の原因となります。変圧器の並列運転において、この循環電流を最小限に抑えることは重要な課題です。循環電流の大きさは、変圧器間の電圧差とインピーダンスによって決まります。
■ 計算手順と公式
- 各変圧器の二次電圧の計算
変圧器の一次電圧と巻数比から二次電圧を計算します。
\( V_2 = \frac{V_1}{a} \)
ここで、V2は二次電圧、V1は一次電圧、aは巻数比(一次巻数/二次巻数)です。
- 変圧器間の電圧差の計算
並列接続された変圧器の二次電圧の差を求めます。
\( \Delta V = V_{2A} - V_{2B} \)
ここで、ΔVは電圧差、V2AとV2Bはそれぞれの変圧器の二次電圧です。
- 循環電流の計算
変圧器間の電圧差と各変圧器のインピーダンスから循環電流を計算します。
\( I_{circ} = \frac{\Delta V}{Z_A + Z_B} \)
ここで、Icircは循環電流、ZAとZBはそれぞれの変圧器のインピーダンスです。
- 複素数の絶対値計算
循環電流が複素数の場合、その大きさ(絶対値)を計算します。
\( |I| = \frac{|\Delta V|}{\sqrt{R^2 + X^2}} \)
ここで、|I|は電流の大きさ、Rはインピーダンスの実部(抵抗)、Xはインピーダンスの虚部(リアクタンス)です。
■ 具体的な計算例
問題条件
- 変圧器1の巻数比: \( a_1 = 30.1 \)
- 変圧器2の巻数比: \( a_2 = 30.0 \)
- 一次電圧: \( V_1 = 6600 \ \mathrm{[V]} \)
- 変圧器1のインピーダンス: \( Z_1 = 0.013 + j0.022 \ \mathrm{[\Omega]} \)
- 変圧器2のインピーダンス: \( Z_2 = 0.010 + j0.020 \ \mathrm{[\Omega]} \)
各変圧器の二次電圧の計算
\[ \begin{aligned} V_1 &= \frac{6600}{a_1} \\[5pt] &= \frac{6600}{30.1} \\[5pt] &\approx 219.269 \ \mathrm{[V]} \\[10pt] V_2 &= \frac{6600}{a_2} \\[5pt] &= \frac{6600}{30.0} \\[5pt] &= 220 \ \mathrm{[V]} \end{aligned} \]循環電流の計算
\[ \begin{aligned} I &= \frac{V_2 - V_1}{Z_1 + Z_2} \\[5pt] &= \frac{220 - 219.269}{(0.013 + j0.022) + (0.010 + j0.020)} \\[5pt] &= \frac{0.731}{0.023 + j0.042} \ \mathrm{[A]} \end{aligned} \]循環電流の大きさの計算
\[ \begin{aligned} |I| &= \left| \frac{0.731}{0.023 + j0.042} \right| \\[5pt] &= \frac{0.731}{\sqrt{0.023^2 + 0.042^2}} \\[5pt] &= \frac{0.731}{0.04789} \\[5pt] &\approx 15.26 \ \mathrm{[A]} \\[5pt] &\approx 15.3 \ \mathrm{[A]} \end{aligned} \]結論:循環電流の大きさは 15.3 [A] である。(解答:選択肢(3))
■ 実務上の留意点
変圧器の並列運転と循環電流に関する実務上の留意点は以下の通りです。
- 変圧器を並列運転する際は、理想的には同一の巻数比、%インピーダンス、極性を持つものを選定すべきです。
- 循環電流が大きい場合、変圧器の銅損増加による効率低下や発熱増加のリスクがあります。
- 実務では、タップ切替により巻数比を調整して循環電流を最小化することがあります。
- 異なる容量の変圧器を並列運転する場合、%インピーダンスの比が容量の比に反比例するようにすべきです。
- 循環電流による過負荷を避けるため、変圧器の定格容量に対して余裕を持たせた設計が必要です。
- 無負荷時にも循環電流は流れるため、軽負荷時の効率低下に注意が必要です。