【機械】平成24年 問7|単相変圧器の電圧変動と漏れリアクタンスに関する計算問題
単相変圧器があり,二次側を開放して電流を流さない場合の二次電圧の大きさを \( 100 \) [%] とする。
二次側にリアクトルを接続して力率 \( 0 \) の電流を流した場合,二次電圧は \( 5 \) [%] 下がって \( 95 \) [%] であった。
二次側に抵抗器を接続して,前述と同じ大きさの力率 \( 1 \) の電流を流した場合,二次電圧は \( 2 \) [%] 下がって \( 98 \) [%] であった。
一次巻線抵抗と一次換算した二次巻線抵抗との和は \( 10 \) [\( \Omega \)] である。
鉄損及び励磁電流は小さく,無視できるものとする。
ベクトル図を用いた電圧変動率の計算によく用いられる近似計算を利用して,一次漏れリアクタンスと一次換算した二次漏れリアクタンスとの和 [\( \Omega \)] の値を求めた。
その値として,最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
変圧器の基本的な等価回路
変圧器は電力系統における電圧変換の基本要素です。その動作を理解するために等価回路が用いられます。
変圧器の基本構成と動作原理
変圧器は次の主要部分から構成されます:
・鉄心:磁束を効率よく通すための磁気回路
・一次巻線:入力側の巻線
・二次巻線:出力側の巻線
一次巻線に交流電圧を加えると、交流磁束が鉄心内に発生し、この磁束が二次巻線を鎖交することで二次側に電圧が誘導されます。
理想変圧器の関係式
巻数比(変圧比)a = N1 / N2とすると:
\[ \begin{aligned} \frac{V_1}{V_2} &= \frac{N_1}{N_2} = a \\[10pt] \frac{I_1}{I_2} &= \frac{N_2}{N_1} = \frac{1}{a} \\[10pt] \end{aligned} \]
ここで、V1, V2は一次・二次電圧、I1, I2は一次・二次電流、N1, N2は一次・二次巻数です。
実際の変圧器における要素
実際の変圧器では、以下の要素を考慮する必要があります:
1. 巻線抵抗:銅損(I2R損失)の原因
2. 漏れ磁束:巻線周囲で閉じる磁束(漏れリアクタンスとして表現)
3. 鉄損:ヒステリシス損失と渦電流損失
4. 励磁電流:鉄心を磁化するための電流(無負荷時にも流れる)
等価回路の意義
変圧器の等価回路は、これらの実際の要素を電気回路として表現したものです。等価回路を用いることで、負荷条件による電圧降下や効率の計算、短絡・開放試験の解析などが可能になります。
変圧器の一次換算等価回路
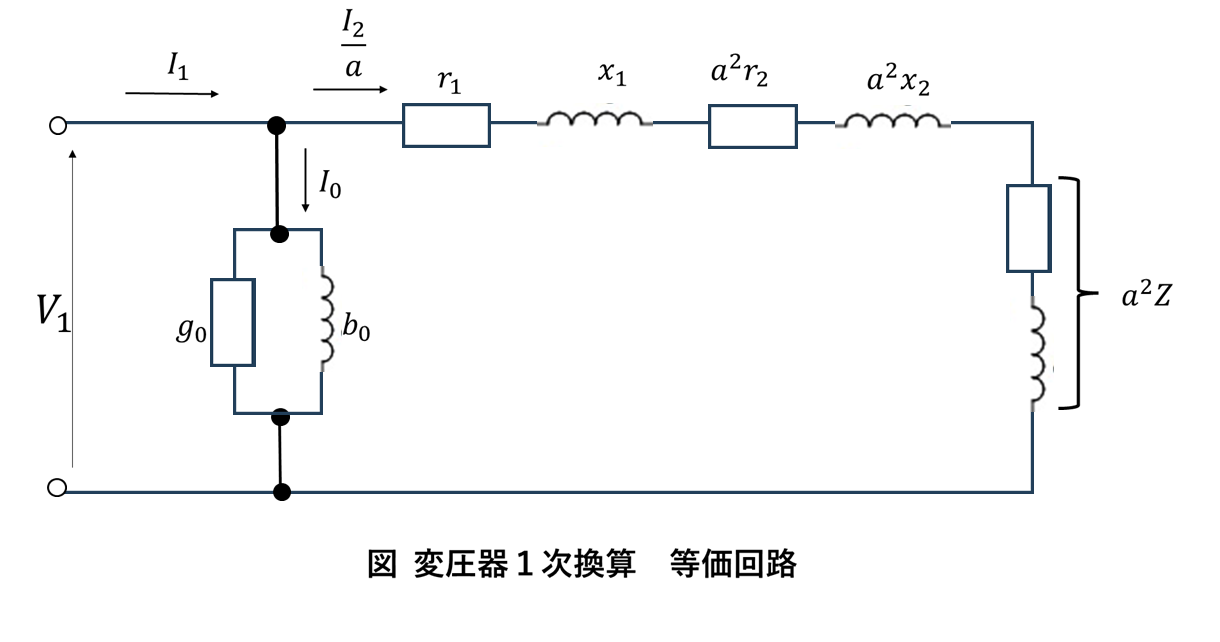
変圧器の一次換算等価回路は、二次側のパラメータを一次側に換算することで、単一の回路として解析を行うものです。
一次換算等価回路の各要素
図に示す各記号の意味は以下の通りです:
\(\dot{V}_1 \; [\mathrm{V}]\):一次側端子電圧
\(I_1 \; [\mathrm{A}]\):一次電流
\(I_2 \; [\mathrm{A}]\):二次電流
\(I_0 \; [\mathrm{A}]\):励磁電流
\(r_1 \; [\Omega]\):一次巻線抵抗
\(r_2 \; [\Omega]\):二次巻線抵抗(一次換算値)
\(x_1 \; [\Omega]\):一次漏れリアクタンス
\(x_2 \; [\Omega]\):二次漏れリアクタンス(一次換算値)
\(a = \frac{N_1}{N_2}\):変圧比
二次側パラメータの一次換算
二次側のパラメータを一次側に換算する際の関係式:
\[ \begin{aligned} r_2' &= a^2 r_2 \\[10pt] x_2' &= a^2 x_2 \\[10pt] V_2' &= a V_2 \\[10pt] I_2' &= \frac{I_2}{a} \\[10pt] Z_2' &= a^2 Z_2 \\[10pt] \end{aligned} \]
ここで、ダッシュ(')は一次換算値を表します。
等価回路の簡略化
解析の目的に応じて、以下のような簡略化が行われることがあります:
1. 励磁回路の省略:負荷電流が励磁電流よりも十分大きい場合
2. 漏れリアクタンスの集約:\(x_1 + x_2 = x\)
3. 巻線抵抗の集約:\(r_1 + r_2 = r\)
等価回路の限界
一次換算等価回路は定常状態における変圧器の特性を表現するものです。過渡現象や非線形特性(磁気飽和など)を表現するには、より詳細なモデルや別の解析手法が必要となります。
変圧器と電力系統の電圧降下
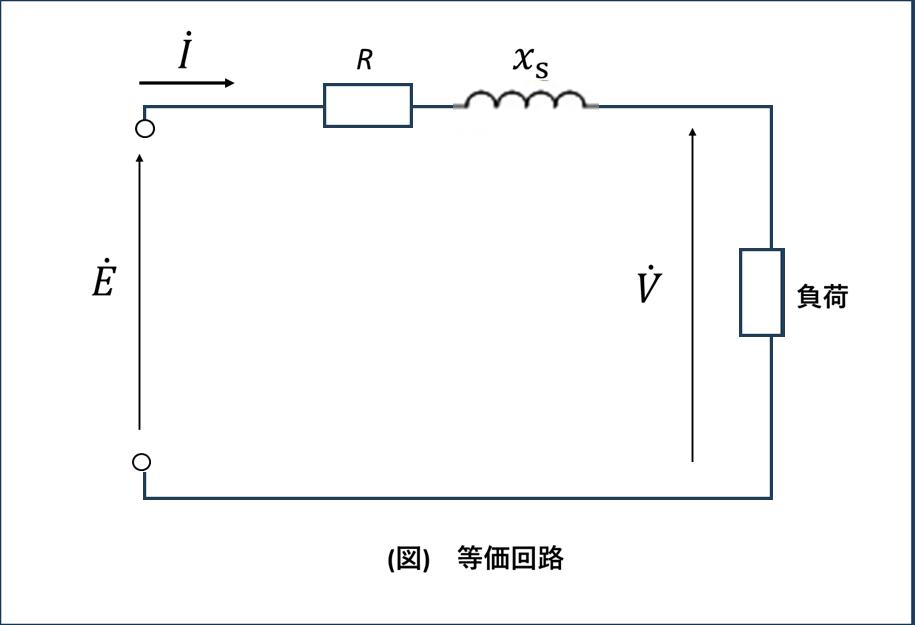
電圧降下の回路図
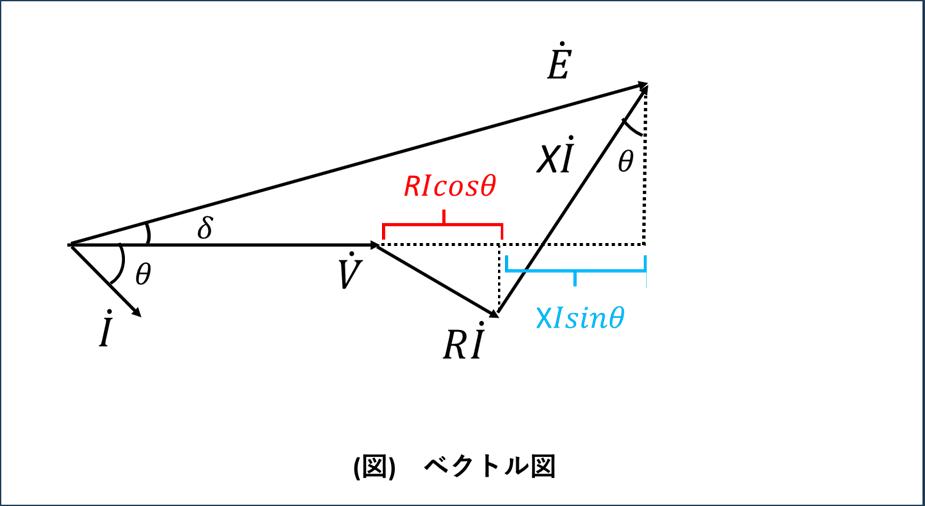
電圧・電流のベクトル図
変圧器や電力系統における電圧降下は、インピーダンスによる電圧降下として解析できます。
電圧降下の近似式
図のような回路において、電源電圧Ėと負荷電圧V̇の位相差が小さい場合、電圧降下ε = E - Vは以下のように近似できます:
\[ \begin{aligned} E &\simeq V + RI\cos\theta + XI\sin\theta \\[10pt] E - V &= RI\cos\theta + XI\sin\theta \\[10pt] \varepsilon &= I(R\cos\theta + X\sin\theta) \\[10pt] \end{aligned} \]
ここで、θは負荷力率角(電流Iと電圧Vの位相差)です。
電圧降下式の物理的意味
この式の各項は次の意味を持ちます:
・\(RI\cos\theta\):抵抗による有効電圧降下(有効電流成分による)
・\(XI\sin\theta\):リアクタンスによる無効電圧降下(無効電流成分による)
力率\(\cos\theta\)によって電圧降下の大きさが変化します:
・抵抗性負荷(\(\cos\theta \approx 1\)):主に抵抗による電圧降下
・誘導性負荷(遅れ力率):抵抗とリアクタンスによる電圧降下の和
・容量性負荷(進み力率):抵抗による電圧降下とリアクタンスによる電圧上昇の差
電圧降下とベクトル図の関係
ベクトル図では\(E = V + (R + jX)I\)と表現されますが、位相差が小さい場合の近似として、上記の式が使われます。この近似は\(E\)と\(V\)のベクトルがほぼ同方向(位相差が小さい)という条件で成り立ちます。
近似式の適用限界
以下の場合には近似式の精度が低下します:
・負荷が大きく、電圧降下が大きい場合(10%以上)
・極端な力率(大きく進みまたは遅れる力率)の負荷
・非線形負荷や高調波を含む場合
このような場合は、ベクトル図に基づく厳密な計算や複素数計算が必要です。
変圧器の電圧降下計算例
変圧器の電圧降下を計算する方法と具体的な数値例を示します。
変圧器の電圧変動率
変圧器の電圧変動率εV [%]は、無負荷時の二次電圧V0と全負荷時の二次電圧VFLの差を、全負荷時の二次電圧で割った値として定義されます:
\[ \begin{aligned} \varepsilon_V &= \frac{V_0 - V_{FL}}{V_{FL}} \times 100\% \\[10pt] \end{aligned} \]
等価回路を用いた計算では、一次換算等価回路のインピーダンスによる電圧降下から求めることができます。
計算例1: 無負荷と全負荷の電圧差
100kVA, 6600V/400V変圧器の等価回路パラメータ:
等価抵抗 r = 5Ω (一次換算)
等価リアクタンス x = 12Ω (一次換算)
定格電流 \[I_{1} = 15.2\mathrm{A}\] (一次側)
負荷力率 cosθ = 0.8 (遅れ)
sinθ = 0.6
電圧降下ε:
\[ \begin{aligned} \varepsilon &= I(r \cos\theta + x \sin\theta) \\[10pt] &= 15.2 \times (5 \times 0.8 + 12 \times 0.6) \\[10pt] &= 15.2 \times (4 + 7.2) \\[10pt] &= 15.2 \times 11.2 \\[10pt] &= 170.2\mathrm{V} \end{aligned} \]
電圧変動率:
\[ \begin{aligned} \varepsilon_V &= \frac{170.2}{6600} \times 100\% = 2.58\% \end{aligned} \]
計算例2: 力率による電圧降下の変化
同じ変圧器で力率が異なる場合の電圧降下:
力率1.0の場合(抵抗性負荷)
cosθ = 1.0, sinθ = 0
\[ \begin{aligned} \varepsilon &= 15.2 \times (5 \times 1.0 + 12 \times 0) = 76\mathrm{V} \\[10pt] \varepsilon_V &= \frac{76}{6600} \times 100\% = 1.15\% \end{aligned} \]
力率0.6の遅れの場合(誘導性負荷)
cosθ = 0.6, sinθ = 0.8
\[ \begin{aligned} \varepsilon &= 15.2 \times (5 \times 0.6 + 12 \times 0.8) \\[10pt] &= 15.2 \times (3 + 9.6) = 192\mathrm{V} \\[10pt] \varepsilon_V &= \frac{192}{6600} \times 100\% = 2.91\% \end{aligned} \]
力率0.8の進みの場合(容量性負荷)
cosθ = 0.8, sinθ = -0.6
\[ \begin{aligned} \varepsilon &= 15.2 \times (5 \times 0.8 + 12 \times (-0.6)) \\[10pt] &= 15.2 \times (4 - 7.2) = -48.6\mathrm{V} \\[10pt] \varepsilon_V &= \frac{-48.6}{6600} \times 100\% = -0.74\% \end{aligned} \]
計算結果の解釈
・抵抗性負荷では電圧降下は小さい
・誘導性負荷(遅れ力率)では電圧降下が大きくなる
・容量性負荷(進み力率)では電圧降下が負になる(電圧上昇)
この性質は変圧器の電圧調整や電力系統の電圧制御において重要です。
変圧器の特性方程式
変圧器の電気的特性を表す基本的な方程式と関係について解説します。
理想変圧器の基本式
理想変圧器の電圧・電流関係:
\[ \begin{aligned} \frac{V_1}{V_2} &= \frac{N_1}{N_2} = a \\[10pt] \frac{I_1}{I_2} &= \frac{N_2}{N_1} = \frac{1}{a} \\[10pt] V_1 I_1 &= V_2 I_2 \quad \text{(電力の保存)} \\[10pt] \end{aligned} \]
実際の変圧器の方程式
一次換算等価回路における電圧方程式:
\[ \begin{aligned} \dot{V}_1 &= \dot{E}_1 + (r_1 + jx_1)\dot{I}_1 \\[10pt] \dot{E}_2 &= \dot{V}_2 + (r_2 + jx_2)\dot{I}_2 \\[10pt] \dot{E}_1 &= \dot{E}_2' = a\dot{E}_2 \\[10pt] \dot{I}_0 &= \dot{I}_h + \dot{I}_m = \frac{\dot{E}_1}{R_c} + \frac{\dot{E}_1}{jX_m} \\[10pt] \dot{I}_1 &= \dot{I}_0 + \dot{I}_2' = \dot{I}_0 + \frac{\dot{I}_2}{a} \\[10pt] \end{aligned} \]
ここで、
\(\dot{E}_1\), \(\dot{E}_2\):一次・二次の誘導起電力
\(\dot{I}_h\):鉄損電流
\(\dot{I}_m\):磁化電流
\(R_c\):鉄損等価抵抗
\(X_m\):励磁リアクタンス
短絡・開放試験による定数決定
等価回路のパラメータは以下の試験から求められます:
短絡試験:二次側を短絡し、定格電流が流れる程度の低電圧を印加
・漏れインピーダンス \((r_1 + r_2) + j(x_1 + x_2)\) の測定
開放試験:二次側を開放し、定格電圧を印加
・励磁インピーダンス \(R_c \parallel jX_m\) の測定
効率の計算
変圧器の効率\(\eta\) [%]:
\[ \begin{aligned} \eta &= \frac{P_2}{P_1} \times 100\% \\[10pt] &= \frac{P_2}{P_2 + P_{\mathrm{loss}}} \times 100\% \\[10pt] \end{aligned} \]
損失 \(P_{\mathrm{loss}}\) は以下の成分から成ります:
・銅損(\(I^2R\)損失):\(P_{\mathrm{Cu}} = I_1^2r_1 + I_2^2r_2\)
・鉄損(ヒステリシス損失と渦電流損失):\(P_{\mathrm{Fe}} = E_1^2/R_c\)
・漂遊損失:機械的・構造的要因による追加の損失
最大効率の条件
変圧器の効率が最大になるのは、銅損と鉄損が等しくなる負荷条件のときです:
\(P_{\mathrm{Cu}} = P_{\mathrm{Fe}}\)
この条件は通常、定格負荷の70〜80%程度の負荷で達成されるように設計されています。
変圧器の応用と実例
変圧器の等価回路解析が実際の応用においてどのように活用されるかを解説します。
変圧器の種類と用途
1. 電力用変圧器
・発電所から需要家までの電力伝送における電圧変換
・特徴:大容量、高効率、長寿命
2. 配電用変圧器
・配電系統における電圧降下の補償
・特徴:タップ切替による電圧調整機能
3. 計器用変圧器
・電圧・電流の測定用
・特徴:高精度、絶縁性能重視
4. 特殊変圧器
・整流器用、試験用、医療用など
・特徴:用途に応じた特殊設計
等価回路の実用的応用
・電力系統の解析:電圧降下、短絡電流の計算
・保護継電器の設定:過電流保護、差動保護
・電圧調整器の設計:タップ位置と電圧変動の関係
・並列運転の条件検討:インピーダンス比の確認
・高調波の影響評価:共振点の推定
負荷変動と電圧安定性
例えば、6600V/400V, 100kVAの変圧器で、負荷が急増した場合の電圧降下と対策:
・負荷が50%から90%に増加すると、電圧降下は約1.4%から2.5%に増加
・対策1:負荷時タップ切替器(LTC)による電圧調整
・対策2:進相コンデンサの設置による力率改善
・対策3:自動電圧調整器(AVR)の使用
エネルギー効率向上の実例
トップランナー変圧器(高効率変圧器)の採用:
・アモルファス合金鉄心を使用し、従来の珪素鋼板鉄心より鉄損を40%低減
・巻線の断面積増加と高導電率材料の採用による銅損の低減
・最適負荷率での運用による効率の最大化
・無負荷損失の低減による待機電力の削減
実運用上の注意点
・温度上昇:過負荷や高調波による追加損失で絶縁劣化が加速
・突入電流:励磁突入電流は定格電流の5〜10倍に達することがあり、保護協調が必要
・不平衡負荷:三相変圧器での不平衡負荷は追加の損失を発生
・高調波:非線形負荷による高調波電流は追加の損失と騒音の原因
🔍 ワンポイントアドバイス: 変圧器の等価回路を理解する上で最も重要なのは、理想変圧器と実際の変圧器のギャップを埋める各要素(巻線抵抗、漏れリアクタンス、励磁回路)の物理的意味を把握することです。電圧降下の計算では、力率の影響が大きいことに注目してください。遅れ力率(誘導性負荷)では電圧降下が大きく、進み力率(容量性負荷)では電圧が上昇することがあります。これは電力系統の電圧制御において重要な性質です。また、実際の解析では多くの場合、電機子巻線抵抗raは漏れリアクタンスに比べて小さいため、簡略化のために無視されることがあります。
今日は変圧器の電圧降下の問題やで!まずは与えられた等価回路を見てみよか。励磁回路は無視できるから、図4のような簡単な等価回路になるんや。この回路で二次側が開放されてる場合、一次電圧と二次電圧の関係はどうなるやろ?
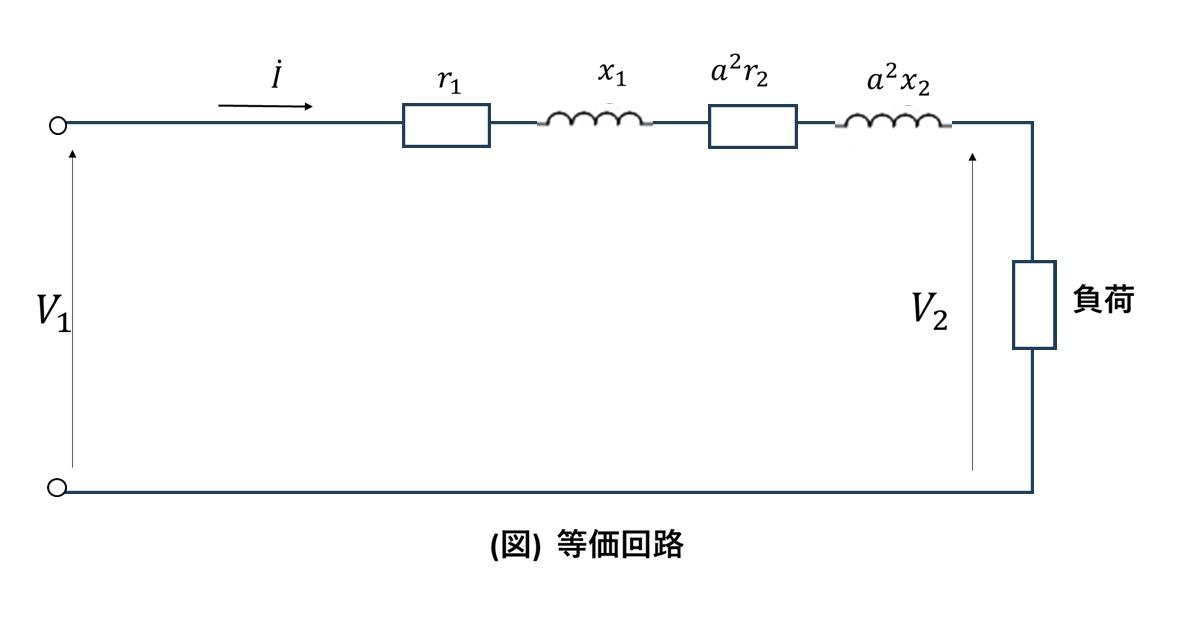
はい、先生!二次側が開放されている場合、回路に電流が流れないので電圧降下は発生しません。つまり、一次電圧 \( \dot{V}_1 \) と二次電圧 \( \dot{V}_2 \) は等しくなります。パーセント表示では \( 100 \ \mathrm{[\%]} \) となります。
その通りや!電流が流れへんから電圧降下がゼロになって、\( \dot{V}_1 = \dot{V}_2 = 100 \ \mathrm{[\%]} \) になるんや。さて、次に無効電力を扱うリアクトル \( x \) を接続した場合を考えよか。この場合、電圧降下 \( \varepsilon \) はどうなるか考えてみよう。電圧降下の近似式は:
\[ \begin{eqnarray} \varepsilon &=& I_1 \left\{ (r_1 + a^2r_2)\cos\theta + (x_1 + a^2x_2)\sin\theta \right\} \\[20pt] \end{eqnarray} \]リアクトル接続時は力率角 \( \theta = \frac{\pi}{2} \) やから、この式どうなる?
はい、先生!リアクトル接続時は純粋な無効電力負荷なので、力率角が \( \theta = \frac{\pi}{2} \) となります。この角度を代入すると:
\[ \begin{eqnarray} \varepsilon &=& I_1 \left\{ (r_1 + a^2r_2)\cos\frac{\pi}{2} + (x_1 + a^2x_2)\sin\frac{\pi}{2} \right\} \\[20pt] \end{eqnarray} \]ここで \( \cos\frac{\pi}{2} = 0 \) と \( \sin\frac{\pi}{2} = 1 \) ですので:
\[ \begin{eqnarray} \varepsilon &=& I_1 \left\{ (r_1 + a^2r_2) \times 0 + (x_1 + a^2x_2) \times 1 \right\} \\[20pt] &=& (x_1 + a^2x_2) I_1 \end{eqnarray} \]また、問題文より電圧降下は \( \varepsilon = 0.05V_2 = 0.05V_1 \) なので:
\[ \begin{eqnarray} 0.05V_1 &=& (x_1 + a^2x_2) I_1 \quad \ldots ① \end{eqnarray} \]ええやん!リアクトル接続時の式がちゃんと導けたな。次は有効電力を扱う抵抗 \( r \) を接続した場合も考えてみよか。この場合は力率角 \( \theta = 0 \) で、電圧降下は \( \varepsilon = 0.02V_1 \) やな。同じように電圧降下の式を立てると:
\[ \begin{eqnarray} \varepsilon &=& I_2 \left\{ (r_1 + a^2r_2)\cos\theta + (x_1 + a^2x_2)\sin\theta \right\} \\[20pt] \end{eqnarray} \]\( \theta = 0 \) の場合、この式どう変わるか説明してみてくれるか?
はい、先生!抵抗 \( r \) を接続した場合は純粋な有効電力負荷なので、力率角は \( \theta = 0 \) です。この角度を代入すると:
\[ \begin{eqnarray} \varepsilon &=& I_2 \left\{ (r_1 + a^2r_2)\cos 0 + (x_1 + a^2x_2)\sin 0 \right\} \\[20pt] \end{eqnarray} \]ここで \( \cos 0 = 1 \) と \( \sin 0 = 0 \) ですので:
\[ \begin{eqnarray} \varepsilon &=& I_2 \left\{ (r_1 + a^2r_2) \times 1 + (x_1 + a^2x_2) \times 0 \right\} \\[20pt] &=& (r_1 + a^2r_2) I_2 \end{eqnarray} \]問題文より電圧降下は \( \varepsilon = 0.02V_2 = 0.02V_1 \) なので:
\[ \begin{eqnarray} 0.02V_1 &=& (r_1 + a^2r_2) I_2 \end{eqnarray} \]よしよし、\( V_1 = 500 I_1 \) が求まったな。次にこの関係式をリアクトル接続時の式①に代入していこか。式①を覚えてるか?
はい、先生!式①は \( 0.05V_1 = (x_1 + a^2x_2) I_1 \) でした。ここに先ほど求めた \( V_1 = 500 I_1 \) を代入してみます:
\[ \begin{eqnarray} 0.05V_1 &=& (x_1 + a^2x_2) I_1 \\[20pt] 0.05 \times 500 I_1 &=& (x_1 + a^2x_2) I_1 \\[20pt] 25 I_1 &=& (x_1 + a^2x_2) I_1 \\[20pt] \end{eqnarray} \]\( I_1 \) で両辺を割ると:
\[ \begin{eqnarray} x_1 + a^2x_2 &=& 25 \ \mathrm{[\Omega]} \end{eqnarray} \]よって、答えは選択肢の(5)です。
ようやったな!変圧器の合成リアクタンス \( x_1 + a^2x_2 = 25 \ \mathrm{[\Omega]} \) が求まったで!今回の問題のポイントをまとめよか?
はい、先生!この問題から学んだポイントは:
1. 変圧器の電圧降下は負荷の種類(有効・無効)によって異なります。
2. 力率角 \( \theta = \frac{\pi}{2} \)(純粋な無効電力負荷)の場合、電圧降下は \( \varepsilon = (x_1 + a^2x_2) I \) となります。
3. 力率角 \( \theta = 0 \)(純粋な有効電力負荷)の場合、電圧降下は \( \varepsilon = (r_1 + a^2r_2) I \) となります。
4. 電圧降下の近似式 \( \varepsilon = I \{ (r_1 + a^2r_2)\cos\theta + (x_1 + a^2x_2)\sin\theta \} \) を使って未知のパラメータを求めることができます。
5. 同じ電流値の異なる負荷条件を比較することで、変圧器の等価回路定数を求めることができます。
解説まとめ
リアクトル\( x \)を接続したとき、電圧降下\( \varepsilon \)は、回路に流れる電流を\( I_{1} \)とすると、以下のようになる:
\[ \begin{aligned} \varepsilon &= I_{1} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \cos \theta \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \sin \theta \Big\} \end{aligned} \]
\( \varepsilon = 0.05V_{2} = 0.05V_{1} \)、\( \theta = \dfrac{\pi}{2} \)であるから、
\[ \begin{aligned} 0.05V_{1} &= I_{1} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \cos \dfrac{\pi}{2} \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \sin \dfrac{\pi}{2} \Big\} \\[10pt] &= I_{1} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \times 0 \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \times 1 \Big\} \\[10pt] &= \left( x_{1} + a^{2} x_{2} \right) I_{1} \quad \end{aligned} \]
同様に、抵抗\( r \)を接続したとき、電圧降下\( \varepsilon \)は、回路に流れる電流を\( I_{2} \)とすると、
\[ \begin{aligned} \varepsilon &= I_{2} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \cos \theta \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \sin \theta \Big\} \end{aligned} \]
\( \varepsilon = 0.02V_{2} = 0.02V_{1} \)、\( \theta = 0 \)であるから、
\[ \begin{aligned} 0.02V_{1} &= I_{2} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \cos 0 \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \sin 0 \Big\} \\[10pt] &= I_{2} \Big\{ \left( r_{1} + a^{2} r_{2} \right) \times 1 \\ &\quad + \left( x_{1} + a^{2} x_{2} \right) \times 0 \Big\} \\[10pt] &= \left( r_{1} + a^{2} r_{2} \right) I_{2} \end{aligned} \]
題意より、\( I_{1} = I_{2} \)、\( r_{1} + a^{2} r_{2} = 10\, [\Omega] \)であるから、
\[ \begin{align} 0.02V_{1} &= 10 I_{1} \\ V_{1} &= 500 I_{1} \end{align} \]
これを①式に代入すると、
\[ \begin{align} 0.05V_{1} &= \left( x_{1} + a^{2} x_{2} \right) I_{1} \\ 0.05 \times 500 I_{1} &= \left( x_{1} + a^{2} x_{2} \right) I_{1} \\ 25 I_{1} &= \left( x_{1} + a^{2} x_{2} \right) I_{1} \\ x_{1} + a^{2} x_{2} &= 25\, [\Omega] \end{align} \]
と求められる。