【機械】令和6年 (下期) 問16|降圧チョッパ回路の電流経路と負荷電流の計算に関する問題
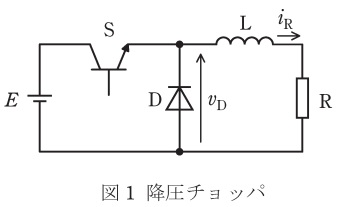
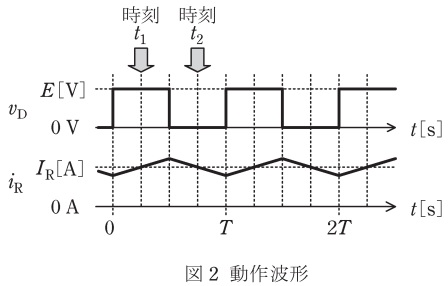
図1に示す降圧チョッパの回路は,電圧 \( E \) の直流電源,スイッチングするパワー半導体デバイス \( \mathrm{S} \),ダイオード \( \mathrm{D} \),リアクトル \( \mathrm{L} \),及び抵抗 \( \mathrm{R} \) の負荷から構成されている。また,図2には,図1の回路に示すダイオード \( \mathrm{D} \) の電圧 \( v_{\mathrm{D}} \) と負荷の電流 \( i_{\mathrm{R}} \) の波形を示す。次の (a) 及び (b) の問に答えよ。
(a) 降圧チョッパの回路動作に関し,図3~図5に,実線で示した回路に流れる電流のループと方向を示した三つの電流経路を考える。図2の時刻 \( t_{1} \) 及び時刻 \( t_{2} \) において,それぞれどの電流経路となるか。正しい組合せを次の (1)~(5) のうちから一つ選べ。
\[ \begin{array}{ccc} & 時刻\ t_{1} & 時刻\ t_{2} \\ \hline (1) & 電流経路\left( \mathrm{C} \right) & 電流経路\left( \mathrm{B} \right) \\ \hline (2) & 電流経路\left( \mathrm{A} \right) & 電流経路\left( \mathrm{C} \right) \\ \hline (3) & 電流経路\left( \mathrm{B} \right) & 電流経路\left( \mathrm{A} \right) \\ \hline (4) & 電流経路\left( \mathrm{B} \right) & 電流経路\left( \mathrm{C} \right) \\ \hline (5) & 電流経路\left( \mathrm{A} \right) & 電流経路\left( \mathrm{B} \right) \\ \hline \end{array} \](b) 電圧 \( E \) が \( 100 \) [V],降圧チョッパの通流率が \( 50\,\% \),負荷抵抗 \( R \) が \( 2 \) [Ω] とする。パワー半導体デバイス \( \mathrm{S} \) は周期 \( T \) の高周波でスイッチングし,リアクトル \( \mathrm{L} \) の平滑作用により,図2に示す電流 \( i_{\mathrm{R}} \) のリプル成分は十分小さいとする。電流 \( i_{\mathrm{R}} \) の平均値 \( I_{\mathrm{R}} \) [A] として,最も近いものを次の (1)~(5) のうちから一つ選べ。

合格への方程式
降圧チョッパの基本原理
降圧チョッパって何?
降圧チョッパは、直流の電圧を下げる(降圧する)ための電子回路です。「チョッパ」という名前は、電圧を細かく「刻む(chop)」ことから来ています。
降圧チョッパの特徴
- 入力:高い直流電圧
- 出力:低い直流電圧(平均値として)
- 方式:スイッチングによる電圧制御
- 効率:非常に高い(95%以上も可能)
回路の構成要素
降圧チョッパは5つの主要な部品で構成されています:
各部品の役割
- 電源E:入力となる直流電圧源
- スイッチS:高速でオン・オフするパワー半導体(MOSFET、IGBTなど)
- ダイオードD:還流ダイオード、逆流防止の役割
- リアクトルL:エネルギー蓄積と平滑化
- 負荷R:電力を消費する抵抗負荷
動作の基本原理
降圧チョッパは、スイッチを高速でオン・オフすることで動作します:
動作のイメージ
- スイッチオン時:電源から負荷に電流が流れ、リアクトルにエネルギーを蓄積
- スイッチオフ時:リアクトルに蓄積されたエネルギーが負荷に供給
- 繰り返し:この動作を高周波(数kHz〜数MHz)で繰り返す
- 結果:平均的に見ると入力より低い電圧が出力される
なぜ高効率なのか?
従来の線形レギュレータと比較して、チョッパ方式が高効率な理由:
| 方式 | 原理 | 効率 | 発熱 |
|---|---|---|---|
| 線形方式 | 抵抗で電圧降下 | 50~80% | 大きい |
| チョッパ方式 | スイッチング制御 | 85~98% | 小さい |
身近な応用例
日常生活での降圧チョッパ
- スマホ充電器:AC100VからDC5Vへの変換
- PC電源:12Vから3.3V、1.2Vなどへの変換
- LED照明:定電流制御による明るさ調整
- 電気自動車:バッテリー電圧の最適化
- 太陽光発電:MPPT制御による最大電力追従
チョッパとトランスの違い
電圧を下げる方法として、トランスもありますが違いは:
比較
- トランス:交流専用、大型・重い、変圧比固定
- チョッパ:直流専用、小型・軽量、電圧可変制御
- 組み合わせ:AC→DC変換ではトランス→チョッパの組み合わせも使用
注意点
- スイッチング雑音:高周波ノイズが発生する
- 制御の複雑さ:フィードバック制御が必要
- 部品の選定:高周波特性を考慮した部品が必要
回路動作と電流経路
スイッチオン時の動作
スイッチSがオンになると、以下の電流経路が形成されます:
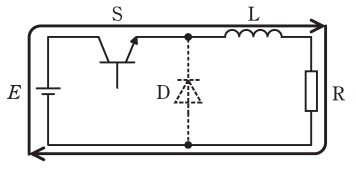
スイッチオン時の電流経路(A)
- 電流の流れ:電源E → スイッチS → リアクトルL → 負荷R → 電源E
- ダイオードD:逆方向電圧がかかり、電流は流れない(オフ状態)
- リアクトルL:電流増加によりエネルギーを蓄積
- ダイオード電圧:\(v_D = E\)(電源電圧と同じ)
スイッチオフ時の動作
スイッチSがオフになると、電流経路が変わります:
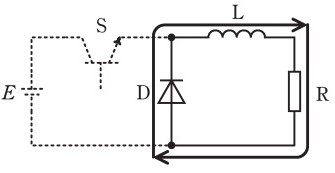
スイッチオフ時の電流経路(B)
- 電流の流れ:リアクトルL → 負荷R → ダイオードD → リアクトルL
- 電源E:回路から切り離される
- ダイオードD:順方向となり電流が流れる(オン状態)
- ダイオード電圧:\(v_D = 0\)(順方向降下電圧≒0V)
リアクトルの役割
リアクトル(インダクタ)は降圧チョッパで最重要の部品です:
リアクトルの働き
- エネルギー蓄積:スイッチオン時に磁気エネルギーとして蓄積
- エネルギー放出:スイッチオフ時に蓄積したエネルギーを負荷に供給
- 電流の連続性:急激な電流変化を防ぐ
- 平滑効果:出力電流のリプル(変動)を小さくする
ダイオードの電圧波形の読み方
問題で与えられるダイオード電圧 \(v_D\) の波形から、スイッチの状態が分かります:
波形の読み取り方
- \(v_D = E\):ダイオードに逆電圧 → ダイオードオフ → スイッチオン
- \(v_D = 0\):ダイオードに順電圧 → ダイオードオン → スイッチオフ
- 時刻\(t_1\):\(v_D = E\) なのでスイッチオン → 電流経路(A)
- 時刻\(t_2\):\(v_D = 0\) なのでスイッチオフ → 電流経路(B)
電流の連続・不連続動作
負荷の大きさによって、電流の流れ方が変わります:
| 動作モード | 電流の特徴 | 発生条件 | 制御への影響 |
|---|---|---|---|
| 連続導通 | 電流が常に流れ続ける | 重い負荷 | 制御が安定 |
| 不連続導通 | 電流がゼロになる期間がある | 軽い負荷 | 制御が複雑 |
スイッチング周波数の影響
周波数の選定
- 高周波化のメリット:リアクトル小型化、応答性向上
- 高周波化のデメリット:スイッチング損失増大、ノイズ増加
- 一般的な範囲:数十kHz~数MHz
- 最適化:効率とサイズのトレードオフで決定
実際の波形の特徴
各部の電圧・電流波形
- スイッチ電圧:オン時0V、オフ時E(方形波)
- ダイオード電圧:オン時0V、オフ時E(スイッチと逆位相)
- 出力電流:鋸歯状波(三角波)
- 平均出力電圧:入力電圧×通流率
波形解析の注意点
- 理想化した波形:実際にはスイッチング時間や配線インダクタンスの影響がある
- ダイオードの順方向電圧:実際には0.7V程度の電圧降下がある
- スイッチングノイズ:高周波成分によるスパイクが発生
出力電圧と通流率
通流率とは?
通流率(デューティ比)は、降圧チョッパの出力電圧を決める最重要パラメータです。
通流率の定義
ここで:
- \(T_{ON}\):スイッチがオンの時間
- \(T_{OFF}\):スイッチがオフの時間
- \(T\):スイッチングの周期 \((T = T_{ON} + T_{OFF})\)
- \(\gamma\):通流率(0~1の値)
出力電圧の計算
降圧チョッパの平均出力電圧は、通流率で簡単に計算できます:
\[ V_o = \gamma \cdot E \]通流率と出力電圧の関係
- \(\gamma = 0\):スイッチ常時オフ → \(V_o = 0\)
- \(\gamma = 0.5\):オン・オフ時間が同じ → \(V_o = E/2\)
- \(\gamma = 1\):スイッチ常時オン → \(V_o = E\)
なぜこの式が成り立つのか?
出力電圧が通流率に比例する理由を詳しく見てみましょう:
出力電圧の導出
- スイッチオン時:負荷には電源電圧Eがかかる
- スイッチオフ時:負荷にはリアクトルからの電圧(≈0V)がかかる
- 1周期の平均:\(V_o = \frac{E \cdot T_{ON} + 0 \cdot T_{OFF}}{T}\)
- 整理すると:\(V_o = E \cdot \frac{T_{ON}}{T} = \gamma E\)
問題の具体的計算
問題の条件で計算してみましょう:
- 電源電圧:\(E = 100\)V
- 通流率:\(\gamma = 50\% = 0.5\)
- 負荷抵抗:\(R = 2\)Ω
負荷電流の計算
平均出力電圧が分かれば、オームの法則で負荷電流を求められます:
\[ \begin{aligned} I_R &= \frac{V_o}{R} \\[10pt] &= \frac{50}{2} \\[10pt] &= 25 \text{ A} \end{aligned} \]電流リプルと平滑効果
実際の出力電流は完全な直流ではなく、わずかに変動(リプル)があります:
電流リプルの特徴
- リプル周波数:スイッチング周波数と同じ
- リプル振幅:リアクトル値に反比例
- 平滑化:リアクトルとキャパシタで小さくできる
- 問題での仮定:「十分小さい」として無視
効率の計算
理想的な降圧チョッパでは、入力電力と出力電力が等しくなります:
\[ \eta = \frac{P_{out}}{P_{in}} = \frac{V_o \cdot I_o}{E \cdot I_{in}} \times 100\% \]問題の場合の効率計算例
- 出力電力:\(P_{out} = V_o \cdot I_R = 50 \times 25 = 1250\)W
- 理想的な場合:\(\eta = 100\%\)(損失無し)
- 実際の場合:\(\eta = 85\sim95\%\)(スイッチング損失等あり)
設計上の考慮事項
| パラメータ | 影響 | 設計指針 |
|---|---|---|
| 通流率 | 出力電圧を決定 | 0.2~0.8の範囲が一般的 |
| スイッチング周波数 | 部品サイズと効率 | 高すぎると損失増大 |
| リアクトル値 | 電流リプル | 大きいとリプル減少、サイズ増大 |
実用上の制限
- 最小オン時間:スイッチに物理的な最小オン時間がある
- 最小オフ時間:ダイオードの回復時間が必要
- デッドタイム:同時オンによる短絡防止
問題解法テクニック
電験三種での出題パターン
降圧チョッパの問題は、主に以下のパターンで出題されます:
頻出問題タイプ
- 電流経路の特定:スイッチ状態から電流の流れを判断
- 出力電圧・電流の計算:通流率からの平均値計算
- 波形解析:ダイオード電圧波形からスイッチ状態を推定
- 部品の役割:各素子の機能と必要性
電流経路問題の解法
解法手順
- ダイオード電圧を確認:\(v_D\) の値からスイッチ状態を判断
- スイッチ状態の確認:オン/オフを明確にする
- 電流経路をトレース:実際に回路上で電流の流れを追う
- 選択肢と照合:該当する電流経路を選択
判断基準の覚え方
- 「ダイオード電圧高い → スイッチオン」
- 「ダイオード電圧ゼロ → スイッチオフ」
- 「スイッチオン → 電源から電流」
- 「スイッチオフ → リアクトルから電流」
出力計算問題の解法
計算手順
- 通流率の確認:問題文から \(\gamma\) を読み取る
- 平均出力電圧計算:\(V_o = \gamma \times E\)
- 負荷電流計算:\(I_R = V_o / R\)
- 単位・桁数の確認:計算結果の妥当性をチェック
計算のチェックポイント
- 通流率の単位:%表示を小数に変換(50% → 0.5)
- 電圧の大小関係:出力 < 入力であることを確認
- オームの法則:\(I = V/R\) を正しく適用
- 有効数字:問題に応じた精度で計算
よくある間違いとその対策
典型的な間違いパターン
- スイッチ状態の誤判断:ダイオード電圧の読み間違い
- 電流方向の間違い:ダイオードの極性を無視
- 通流率の計算ミス:パーセントと小数の変換忘れ
- 平均値と瞬時値の混同:出力は平均値で計算
効率的な解答テクニック
時間短縮のコツ
- 公式の暗記:\(V_o = \gamma E\) は必須暗記
- 波形の特徴:ダイオード電圧の典型パターンを覚える
- 概算での確認:計算結果が常識的範囲内かチェック
- 選択肢の活用:明らかに違う選択肢を先に除外
類似問題への応用
降圧チョッパで学んだ知識は、他の電力変換回路でも応用できます:
| 回路種類 | 機能 | 共通する考え方 |
|---|---|---|
| 昇圧チョッパ | 電圧を上げる | スイッチング制御、エネルギー蓄積 |
| インバータ | DC→AC変換 | スイッチング、PWM制御 |
| コンバータ | AC→DC変換 | 整流、平滑回路 |
実務での知識活用
実際の設計・保守での応用
- 電源設計:効率とサイズのバランス検討
- ノイズ対策:スイッチングノイズの抑制方法
- 故障診断:波形異常からの故障箇所特定
- 保護回路:過電流・過電圧保護の設計
最終チェックリスト
試験前の確認項目
- □ 降圧チョッパの基本動作原理
- □ スイッチオン/オフ時の電流経路
- □ ダイオード電圧からスイッチ状態の判断
- □ 通流率の定義:\(\gamma = \frac{T_{ON}}{T}\)
- □ 出力電圧公式:\(V_o = \gamma \times E\)
- □ 負荷電流計算:\(I = V/R\)
- □ パーセント表示の小数変換
- □ リアクトルの役割(エネルギー蓄積・平滑化)
頻出計算パターンの暗記
典型的な数値例
- 通流率50%:\(\gamma = 0.5\) → 出力は入力の半分
- 電源100V、通流率50%:出力50V
- 負荷2Ω、出力50V:電流25A
- 基本的な比例関係:通流率が2倍 → 出力電圧も2倍
問題文の読み取りポイント
- 「平滑作用により十分小さい」:リプルは無視して平均値で計算
- 「パワー半導体デバイス」:理想スイッチとして扱う
- 「高周波でスイッチング」:周波数の具体値は通常不要
- 「最も近いもの」:厳密でなく概算で十分
🔍 ワンポイントアドバイス:降圧チョッパは「ダイオード電圧でスイッチ状態を判断」「通流率で出力電圧が決まる」の2つが最重要!ダイオード電圧が高い時はスイッチオン(電流経路A)、ゼロの時はスイッチオフ(電流経路B)。出力計算は単純で「出力電圧 = 通流率 × 入力電圧」を覚えれば即座に解けます。パーセント表示を小数に変換することを忘れずに!
よっしゃ!今日は降圧チョッパの問題やな。パワーエレクトロニクスは動作原理の理解が命やから、回路の電流の流れをしっかり追いかけながら解説するで!まず降圧チョッパって何か、基本から教えてくれる?
はい!降圧チョッパは、直流電圧を下げる(降圧する)ためのパワーエレクトロニクス回路ですね。
基本構成は:
・直流電源\(E\)
・スイッチング素子\(S\)(パワー半導体デバイス)
・還流ダイオード\(D\)
・平滑リアクトル\(L\)
・負荷抵抗\(R\)
スイッチ\(S\)を高速でオン・オフすることで、入力直流電圧より低い平均電圧を出力に得ることができる回路です。
その通りや!基本はばっちりやな。ほんで、この回路の肝は「スイッチがオンの時」と「スイッチがオフの時」で電流の流れる経路が変わることなんや。まず、スイッチがオンになった時の電流経路を見てみよか。
スイッチオン

この状態で電流はどう流れる?
スイッチ\(S\)がオンの時:
・電源\(E\)から電流が流れ出す
・スイッチ\(S\)を通って電流が流れる
・リアクトル\(L\)と抵抗\(R\)に電流が流れる
・ダイオード\(D\)には逆方向の電圧がかかるので電流は流れない
この時、リアクトル\(L\)にはエネルギーが蓄積されていきます。電流経路は:
電源\(E\) → スイッチ\(S\) → リアクトル\(L\) → 負荷\(R\) → 電源\(E\)

完璧や!スイッチオン時の動作がちゃんと分かってるやん。ほんで、この時にダイオード\(D\)の両端電圧\(v_D\)はどうなると思う?電源電圧を\(E\)とした時や。
スイッチ\(S\)がオンの時、ダイオード\(D\)の両端電圧を考えてみます。
・スイッチ\(S\)がオンなので、スイッチの両端電圧は約\(0\,\mathrm{V}\)
・よって、ダイオードのアノード側は電源の負極と同電位
・ダイオードのカソード側は電源の正極と同電位
したがって、ダイオード\(D\)には逆方向に電源電圧\(E\)がかかり:
\(v_D = E\,\mathrm{[V]}\)(逆方向電圧)
この状態ではダイオードは導通せず、電流は流れません。
すばらしい理解や!ダイオードの電圧がちゃんと分かってるな。次はスイッチがオフになった時や。この時の電流経路を見てみよか。
スイッチオフ

スイッチがオフになると何が起こる?
スイッチ\(S\)がオフの時:
・スイッチ\(S\)が開放されるので、電源\(E\)からは電流が流れなくなる
・しかし、リアクトル\(L\)に蓄積されていたエネルギーがある!
・リアクトルは電流の変化を嫌うので、蓄積エネルギーを放出して電流を継続させようとする
・この時、ダイオード\(D\)が順方向になって導通し、還流経路を作る
電流経路は:
リアクトル\(L\) → 負荷\(R\) → ダイオード\(D\) → リアクトル\(L\)
これが「還流回路」と呼ばれる動作ですね。

完璧や!還流動作の理解もばっちりやな。ほんで、スイッチオフの時、ダイオード\(D\)の電圧\(v_D\)はどうなる?今度はダイオードが導通してるからな。
スイッチ\(S\)がオフの時:
・ダイオード\(D\)が順方向で導通している
・導通しているダイオードの順方向電圧降下は非常に小さい(理想的には\(0\,\mathrm{V}\))
したがって:
\(v_D = 0\,\mathrm{[V]}\)
これで、問題の波形図で\(v_D\)が\(E\)と\(0\)の間で切り替わっている理由がよく分かりますね!
・\(v_D = E\):スイッチオン時(ダイオード逆バイアス)
・\(v_D = 0\):スイッチオフ時(ダイオード順方向導通)
ええ理解や!動作原理がちゃんと分かったところで、(a)の問題を解いてみよか。図2の波形を見て、時刻\(t_1\)と\(t_2\)で\(v_D\)がどんな値になってるか確認してみて。
図2の波形を見ると:
**時刻\(t_1\):**
・ダイオード電圧\(v_D = E\,\mathrm{[V]}\)
・これは先ほど学んだように、スイッチ\(S\)が**オン**の状態
・したがって電流経路(A):電源→スイッチ→負荷
**時刻\(t_2\):**
・ダイオード電圧\(v_D = 0\,\mathrm{[V]}\)
・これはスイッチ\(S\)が**オフ**の状態
・したがって電流経路(B):還流回路(リアクトル→負荷→ダイオード)
答えは:\(t_1\)で電流経路(A)、\(t_2\)で電流経路(B)
その通りや!(a)は(5)が正解やな。次は(b)の計算問題や。降圧チョッパの出力電圧を求める公式を覚えてるか?通流率\(\gamma\)っていう重要な概念があるんやけど。
はい!降圧チョッパの出力電圧公式ですね。
**通流率\(\gamma\)**は:
\[ \gamma = \frac{T_{\mathrm{ON}}}{T_{\mathrm{ON}} + T_{\mathrm{OFF}}} = \frac{T_{\mathrm{ON}}}{T} \]・\(T_{\mathrm{ON}}\):スイッチのオン時間
・\(T_{\mathrm{OFF}}\):スイッチのオフ時間
・\(T\):スイッチング周期
**降圧チョッパの平均出力電圧**は:
\[ V_{\mathrm{o}} = \gamma E \]つまり、入力電圧\(E\)に通流率をかけた値が出力電圧になります。
完璧や!公式もちゃんと覚えてるやん。ほんじゃ問題の条件を整理してみよか。電源電圧\(E = 100\,\mathrm{V}\)、通流率\(\gamma = 50\% = 0.5\)、負荷抵抗\(R = 2\,\mathrm{\Omega}\)やな。まず平均出力電圧\(V_{\mathrm{o}}\)を計算してみて。
平均出力電圧\(V_{\mathrm{o}}\)を計算します:
\[ \begin{aligned} V_{\mathrm{o}} &= \gamma E \\[10pt] &= 0.5 \times 100 \\[10pt] &= 50 \, \mathrm{[V]} \end{aligned} \]通流率が\(50\%\)なので、入力電圧\(100\,\mathrm{V}\)の半分の\(50\,\mathrm{V}\)が出力電圧になりますね。
これは物理的にも納得できます。スイッチが半分の時間だけオンなので、平均すると入力電圧の半分が出力に現れるということですね。
すばらしい理解や!物理的な意味もちゃんと分かってるやん。ほんじゃ最後に、負荷電流の平均値\(I_{\mathrm{R}}\)を求めてみよか。オームの法則を使うだけやで。
負荷電流の平均値\(I_{\mathrm{R}}\)をオームの法則で計算します:
\[ \begin{aligned} I_{\mathrm{R}} &= \frac{V_{\mathrm{o}}}{R} \\[10pt] &= \frac{50}{2} \\[10pt] &= 25 \, \mathrm{[A]} \end{aligned} \]したがって、負荷電流の平均値は\(25\,\mathrm{A}\)となり、答えは(2) \(25.0\)ですね!
完璧や!両方とも正解やな。ところで、この問題で「リプル成分は十分小さい」っていう条件があったけど、これはどういう意味か分かる?
「リプル成分は十分小さい」という条件について説明します:
**リプルとは:**
・スイッチングによって生じる電流や電圧の脈動成分
・理想的には完全に平滑されて直流になるべき
**リアクトル\(L\)の平滑作用:**
・リアクトルは電流の急激な変化を抑制する
・十分大きなリアクタンスがあると、電流がほぼ一定になる
**この条件の意味:**
・負荷電流\(i_{\mathrm{R}}\)は平均値\(I_{\mathrm{R}}\)でほぼ一定
・したがって単純に\(I_{\mathrm{R}} = V_{\mathrm{o}}/R\)で計算できる
実際の回路では多少のリプルが存在しますが、計算を簡単にするための理想化ですね。
ええ説明や!リアクトルの役割もちゃんと理解してるやん。他にも、降圧チョッパで通流率を変えると出力電圧がどう変わるか説明してもらえる?
通流率\(\gamma\)と出力電圧の関係を説明します:
**通流率の変化と出力電圧:**
\(V_{\mathrm{o}} = \gamma E\)なので:
・\(\gamma = 0.1\)(10%)→ \(V_{\mathrm{o}} = 0.1E\)(入力の10%)
・\(\gamma = 0.5\)(50%)→ \(V_{\mathrm{o}} = 0.5E\)(入力の50%)
・\(\gamma = 0.9\)(90%)→ \(V_{\mathrm{o}} = 0.9E\)(入力の90%)
**制御方法:**
・スイッチング周期\(T\)を一定にして、オン時間\(T_{\mathrm{ON}}\)を変える
・これをPWM(Pulse Width Modulation)制御という
**実用性:**
・\(\gamma\)を\(0\)~\(1\)の範囲で変えることで、\(0\)~\(E\)の範囲で出力電圧を自由に制御できる
・これが降圧チョッパの最大の利点ですね!
素晴らしい解説や!PWM制御まで説明できるとは。最後に、この問題のポイントと、パワーエレクトロニクス問題の攻略法をまとめてくれる?
降圧チョッパ問題の攻略ポイントをまとめます:
【動作原理の理解が最重要】
・スイッチオン時:電源→スイッチ→負荷の経路
・スイッチオフ時:リアクトル→負荷→ダイオードの還流経路
・ダイオード電圧:オン時\(E\)、オフ時\(0\)
【重要公式】
・通流率:\(\gamma = \frac{T_{\mathrm{ON}}}{T}\)
・出力電圧:\(V_{\mathrm{o}} = \gamma E\)
・負荷電流:\(I_{\mathrm{R}} = \frac{V_{\mathrm{o}}}{R}\)
【よくある間違い】
・スイッチ状態とダイオード電圧の関係を逆に覚える
・通流率の定義を間違える(オフ時間で割ってしまう)
・パーセント表記を小数に変換し忘れ
【パワエレ攻略法】
1. 回路の動作を時系列で追う
2. 各素子の状態(導通/遮断)を確認
3. エネルギーの流れを理解
4. 平均値の概念を大切に
完璧なまとめや!降圧チョッパは昇圧チョッパ、インバータ、コンバータなど、他のパワエレ回路の基礎になる回路やから、しっかり理解しておいてな。特に「エネルギーの流れ」を意識することが重要やで。お疲れさん!
ありがとうございました!
降圧チョッパの学習を通じて:
1. **パワーエレクトロニクスの基本思想**(スイッチング制御)
2. **エネルギー蓄積・放出の概念**(リアクトルの役割)
3. **平均値による解析手法**(実効的な制御方法)
4. **半導体素子の特性利用**(ダイオードの整流作用)
これらの重要概念がよく理解できました。
現代社会では電力変換技術がますます重要になっているので、これらの基礎をしっかり身につけて、より複雑な回路の理解にも活かしていきたいと思います。
特に再生可能エネルギーの分野でも、こうした技術が不可欠ですからね!
解説まとめ
■ 降圧チョッパとは
降圧チョッパは、直流電圧を任意の低い直流電圧に変換する電力変換回路です。スイッチング素子のオン・オフ制御により、入力電圧より低い平均出力電圧を得ることができます。主要な構成要素は、スイッチング素子S、還流ダイオードD、平滑用リアクトルL、負荷抵抗Rです。高効率で電圧制御が可能なため、スイッチング電源やDC-DCコンバータなどに広く応用されています。
■ 計算手順と公式
- スイッチオン時の動作
電源からスイッチSを通してリアクトルLと負荷Rに電流が流れます。ダイオードDは逆バイアスとなり電流は流れません。
\( v_D = E \)(ダイオード電圧)
- スイッチオフ時の動作
リアクトルLに蓄えられたエネルギーにより、還流ダイオードDを通して電流が流れ続けます。
\( v_D = 0 \)(ダイオード電圧)
- 通流率の定義
スイッチのオン時間の割合を通流率といいます。
\( \gamma = \frac{T_{ON}}{T_{ON} + T_{OFF}} \)
- 平均出力電圧の計算
出力電圧の平均値は入力電圧に通流率を乗じた値となります。
\( V_o = \gamma E \)
- 平均出力電流の計算
オームの法則により負荷電流を求めます。
\( I_R = \frac{V_o}{R} \)
■ 具体的な計算例
問題条件
- 入力電圧:\( E = 100 \) V
- 通流率:\( \gamma = 0.5 \)(50%)
- 負荷抵抗:\( R = 2 \) Ω
- リアクトルLの平滑作用により電流リプルは十分小さい
(a) 電流経路の判定
ダイオード電圧\( v_D \)から動作状態を判定:
- 時刻\( t_1 \):\( v_D = E \) → スイッチON → 電流経路(A)
- 時刻\( t_2 \):\( v_D = 0 \) → スイッチOFF → 電流経路(B)
(b) 平均出力電圧の計算
\[ \begin{aligned} V_o &= \gamma E \\[5pt] &= 0.5 \times 100 \\[5pt] &= 50 \ \mathrm{[V]} \end{aligned} \]平均負荷電流の計算
\[ \begin{aligned} I_R &= \frac{V_o}{R} \\[5pt] &= \frac{50}{2} \\[5pt] &= 25 \ \mathrm{[A]} \end{aligned} \]結論:(a) 時刻\( t_1 \)は電流経路(A)、時刻\( t_2 \)は電流経路(B)で選択肢(5)、(b) 平均電流は25 Aで選択肢(2)
■ 実務上の留意点
降圧チョッパは現代の電力変換技術の基礎となる重要な回路です。設計・運用において以下の点に注意が必要です。
- スイッチング周波数を高くすると、リアクトルやコンデンサを小型化できますが、スイッチング損失が増加します。通常20kHz~数百kHzで動作させます。
- リアクトルLは電流の連続性を保つ重要な役割を果たします。リプル電流を小さくするには十分なインダクタンスが必要です。
- 還流ダイオードDは高速リカバリ型を使用し、逆回復時間による損失を最小化する必要があります。
- 実際の回路では、スイッチング素子としてMOSFETやIGBTが使用され、ゲート駆動回路やスナバ回路も必要となります。
- 電磁ノイズ対策として、入力側にフィルタを設置し、適切な配線レイアウトとシールドが重要です。