【機械】平成23年 問17|三相ダイオード整流回路の損失および出力電圧に関する計算問題
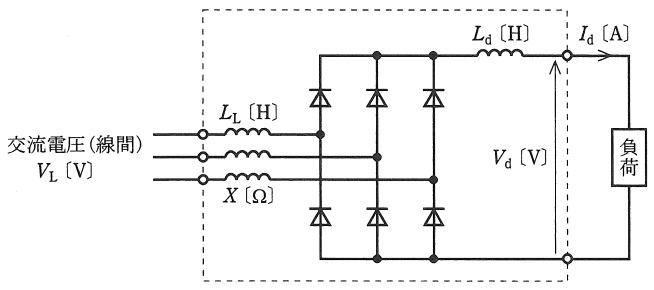
次の図は,バルブデバイスとしてダイオードを用いた三相整流装置の回路を示す。
平滑リアクトルのインダクタンス \( L_{\mathrm{d}} \) [H] は十分に大きく,直流電流 \( I_{\mathrm{d}} \) [A] は一定になっているものとする。
交流側にリアクタンス \( X \) [\( \Omega \)] のリアクトルがあると転流時に重なり角が生じ,直流電圧が降下する。また,ダイオードの順電圧降下 \( V_{\mathrm{F}} \) [V] によっても直流電圧が降下する。これら以外の電圧降下は無視する。
入力交流電圧が \( V_{\mathrm{L}} \) [V] のときのこの整流装置の出力電圧 \( V_{\mathrm{d}} \) [V] は次式で求められる。
\[ \begin{eqnarray} V_{\mathrm{d}} &=& \frac{3\sqrt{2}}{\pi} V_{\mathrm{L}} - \frac{3}{\pi} X \cdot I_{\mathrm{d}} - 2V_{\mathrm{F}} \\[5pt] \end{eqnarray} \]
この整流装置の入力交流電圧は \( V_{\mathrm{L}} = 200 \) [V],周波数は \( f = 50 \) [Hz] で,直流電流は \( I_{\mathrm{d}} = 36 \) [A] である。
交流側のリアクトルのインダクタンスは \( L_{\mathrm{L}} = 5.56 \times 10^{-4} \) [H] で,その抵抗値は平滑リアクトルの抵抗値とともに無視できるものとする。
また,各ダイオードの順電圧降下は \( V_{\mathrm{F}} = 1.0 \) [V] で一定とする。
次の (a) 及び (b) の問に答えよ。
(a) ダイオードでは,電流の通電によって損失が発生する。
一つのダイオードの損失の平均値は,通電する期間が \( 1 \) サイクルの \( \displaystyle \frac{1}{3} \) であるとして計算できる。
一つのダイオードで発生する損失 \( [\mathrm{W}] \) の平均値に最も近いものを次の (1)~(5) のうちから一つ選べ。
(1) \( 12 \) (2) \( 18 \) (3) \( 24 \) (4) \( 36 \) (5) \( 72 \)
(b) 出力電圧 \( V_{\mathrm{d}} \) \( [\mathrm{V}] \) の値として,最も近いものを次の (1)~(5) のうちから一つ選べ。
(1) \( 251 \) (2) \( 262 \) (3) \( 263 \) (4) \( 264 \) (5) \( 270 \)
合格への方程式
整流回路の基礎
整流回路とは
整流回路とは、交流(AC)を直流(DC)に変換する回路です。身近な例では、スマートフォンの充電器やパソコンのACアダプターなどに使われています。電力システムでは、直流送電や電気化学工業などで大容量の整流装置が使用されます。
整流の原理
整流は、ダイオードやサイリスタなどの一方向にしか電流を流さない性質(整流作用)を持つ素子を使って実現されます。これらの素子は「バルブデバイス」とも呼ばれ、電流の流れる方向を制御します。
整流回路の種類
- 単相整流回路:単相交流を直流に変換(家庭用機器に多用)
- 三相整流回路:三相交流を直流に変換(工業用大容量機器に使用)
- 半波整流:交流の半周期のみを利用
- 全波整流:交流の両半周期を利用(効率が良い)
三相整流の利点
三相整流回路は単相整流回路と比較して以下の利点があります:
- 出力電圧のリプル(脈動)が小さい
- 変圧器の利用率が高い
- 大容量化に適している
- 効率が良い
三相整流回路
三相ダイオード整流回路の構成
三相ダイオード整流回路は、3つのダイオードを使った三相半波整流回路と、6つのダイオードを使った三相全波整流回路があります。6ダイオード整流回路は最も一般的な構成です。
理想的な出力電圧
三相全波整流回路の理想的な直流出力電圧は、線間電圧の実効値を VL [V] とすると:
\[ V_{\mathrm{d0}} = \frac{3\sqrt{2}}{\pi} V_{\mathrm{L}} \]で表されます。この式は、三相整流回路の基本的な変換式として重要です。
ダイオードの動作
三相整流回路では、各瞬間において最も電位の高い相のダイオードが導通します。6ダイオード整流では、常に2つのダイオードが導通し、各ダイオードは1サイクルの1/3の期間だけ電流を通します。
平滑リアクトル
整流回路の出力には脈動成分(リプル)が含まれるため、平滑リアクトルを挿入して直流電流を平滑化します。平滑リアクトルのインダクタンスが十分大きい場合、直流電流はほぼ一定となります。
ダイオード特性
ダイオードの基本特性
ダイオードは一方向にのみ電流を流す半導体素子です。順方向に電圧を加えると電流が流れ、逆方向では電流はほとんど流れません(理想的には完全に遮断)。
順電圧降下
実際のダイオードでは、順方向に電流が流れる際に一定の電圧降下が発生します。これを順電圧降下 VF [V] と呼びます。
- シリコンダイオード:約0.7V(一般的)
- ショットキーダイオード:約0.3~0.5V(低損失)
- パワーダイオード:約1.0~1.5V(大電流用)
ダイオードの損失
ダイオードで発生する損失は主に順電圧降下による導通損失です。この損失は:
\[ P_{\mathrm{D}} = V_{\mathrm{F}} \times I_{\mathrm{D(avg)}} \]で計算されます。ここで ID(avg) は通電期間における平均電流です。
三相整流回路でのダイオード電流
三相全波整流回路では、各ダイオードは1サイクルの1/3の期間だけ導通します。直流電流が Id [A] で一定の場合、1つのダイオードの平均電流は:
\[ I_{\mathrm{D}} = \frac{1}{3} I_{\mathrm{d}} \]となります。
電圧降下要因
実際の整流回路の出力電圧
実際の整流回路では、理想値から様々な要因で電圧が降下します。主な要因は以下の通りです:
重なり角による電圧降下
交流側にリアクタンス X [Ω] があると、転流時に重なり角が生じ、電圧降下が発生します。この降下量は:
\[ \Delta V_1 = \frac{3}{\pi} X \cdot I_{\mathrm{d}} \]で表されます。リアクタンス X は、インダクタンス LL [H] と周波数 f [Hz] から:
\[ X = 2\pi f L_{\mathrm{L}} \]で計算されます。
ダイオード順電圧降下による電圧降下
三相全波整流回路では常に2つのダイオードが直列に導通するため、順電圧降下による電圧降下は:
\[ \Delta V_2 = 2 V_{\mathrm{F}} \]となります。
総合的な出力電圧式
これらの電圧降下を考慮した実際の直流出力電圧は:
→ 横スクロールして下さい →
\[ V_{\mathrm{d}} = \frac{3\sqrt{2}}{\pi} V_{\mathrm{L}} - \frac{3}{\pi} X \cdot I_{\mathrm{d}} - 2V_{\mathrm{F}} \]で表されます。この式は三相整流回路の解析において最も重要な式の一つです。
その他の電圧降下要因
- 変圧器の漏れリアクタンス:転流リアクタンスの一部
- 配線抵抗:通常は無視できるレベル
- ダイオードの逆回復電流:高周波では考慮が必要
計算例題
例題1: ダイオード損失の計算
三相整流回路において、直流電流 Id = 36 A、ダイオードの順電圧降下 VF = 1.0 V の場合、1つのダイオードで発生する損失を求めよ。
解答
一つのダイオードが通電する期間は1サイクルの1/3であるから、一つのダイオードに流れる電流の平均値は:
\[ \begin{aligned} I_{\mathrm{D}} &= \frac{1}{3} I_{\mathrm{d}} \\[10pt] &= \frac{1}{3} \times 36 \\[10pt] &= 12 \mathrm{\ [A]} \end{aligned} \]したがって、一つのダイオードで発生する損失は:
\[ \begin{aligned} P_{\mathrm{D}} &= V_{\mathrm{F}} \times I_{\mathrm{D}} \\[10pt] &= 1.0 \times 12 \\[10pt] &= 12 \mathrm{\ [W]} \end{aligned} \]例題2: 出力電圧の計算
入力交流電圧 VL = 200 V、周波数 f = 50 Hz、直流電流 Id = 36 A、交流側インダクタンス LL = 5.56×10⁻⁴ H、ダイオード順電圧降下 VF = 1.0 V の三相整流回路の出力電圧を求めよ。
解答
まず、交流側リアクタンスを計算します:
\[ \begin{aligned} X &= 2\pi f L_{\mathrm{L}} \\[10pt] &= 2\pi \times 50 \times 5.56 \times 10^{-4} \\[10pt] &= 0.175 \mathrm{\ [\Omega]} \end{aligned} \]出力電圧の式に各値を代入すると:
→ 横スクロールして下さい →
\[ \begin{aligned} V_{\mathrm{d}} &= \frac{3\sqrt{2}}{\pi} V_{\mathrm{L}} - \frac{3}{\pi} X \cdot I_{\mathrm{d}} - 2V_{\mathrm{F}} \\[10pt] &= \frac{3\sqrt{2}}{\pi} \times 200 - \frac{3}{\pi} \times 0.175 \times 36 - 2 \times 1.0 \\[10pt] &= 270.1 - 6.0 - 2.0 \\[10pt] &= 262.1 \mathrm{\ [V]} \end{aligned} \]よって、出力電圧は約262Vです。
計算時の注意点
- 角周波数 ω = 2πf の関係を正確に使用する
- ダイオードの導通期間(1/3サイクル)を考慮する
- 三相全波整流では常に2つのダイオードが導通することを忘れない
- 単位変換(特に指数表記)に注意する
- √2 ≈ 1.414、π ≈ 3.14159 の値を適切に使用する
🔍 ワンポイントアドバイス: 三相整流回路の問題では、「理想出力電圧の公式」と「各種電圧降下要因」を分けて考えることが重要です。基本式 Vd0 = (3√2/π)VL をまず覚え、そこから転流リアクタンス降下とダイオード順電圧降下を差し引く手順で計算しましょう。また、ダイオードの導通期間が1/3であることから平均電流を求める考え方は頻出パターンなので確実に理解しておきましょう。
今日は三相整流装置について勉強していくで!図にあるように、ダイオードを使った三相整流回路やな。まず(a)問題から始めていこか。ダイオードの損失について考える問題やで。三相整流回路では、各ダイオードがどのくらいの期間通電するか分かるかな?
はい、三相整流回路でのダイオードの通電期間について確認します。
三相整流回路では、3つのダイオードが順番に導通します。各相が120°ずつ位相差があるため、1つのダイオードが導通する期間は1サイクル(360°)の\(\frac{1}{3}\)となります。
問題文にも「通電する期間が1サイクルの\(\frac{1}{3}\)である」と明記されていますね。
その通りや!各ダイオードは1サイクルの\(\frac{1}{3}\)の期間だけ通電するんやな。問題文によると、直流電流\(I_d = 36\) [A]が一定になっとるから、1つのダイオードに流れる電流の平均値\(I_D\)はどうなるかな?
1つのダイオードに流れる電流の平均値\(I_D\)を求めます。
直流電流\(I_d = 36\) [A]が一定で、各ダイオードは1サイクルの\(\frac{1}{3}\)の期間だけ通電するので:
\[ \begin{aligned} I_D &= \frac{1}{3} \times I_d \\[10pt] &= \frac{1}{3} \times 36 \\[10pt] &= 12 \text{ [A]} \end{aligned} \]したがって、1つのダイオードに流れる電流の平均値は12 [A]となります。
ダイオードの平均電流が12 [A]と求まったな。次に、ダイオードの損失を計算してみようか。ダイオードの順電圧降下\(V_F = 1.0\) [V]やから、損失はどうやって求めるかな?
ダイオードの損失\(P_D\)を求めます。
ダイオードの損失は、順電圧降下と通過する電流の積で求められます:
\[ \begin{aligned} P_D &= V_F \times I_D \\[10pt] &= 1.0 \times 12 \\[10pt] &= 12 \text{ [W]} \end{aligned} \]したがって、1つのダイオードで発生する損失の平均値は12 [W]となります。
これは選択肢の(1)になります。
完璧や!(a)問題の答えは選択肢の(1)やな!
さあ、次は(b)問題や。今度は整流装置の出力電圧\(V_d\)を求める問題やで。与えられた式は:
\( V_d = \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi}X \cdot I_d - 2V_F \)
この式で、リアクタンス\(X\)は何で表されるか分かるかな?インダクタンス\(L_L = 5.56 \times 10^{-4}\) [H]と周波数\(f = 50\) [Hz]が与えられとるで。
リアクタンス\(X\)を求めます。
交流回路におけるインダクタンスのリアクタンス\(X\)は次の式で表されます:
\( X = 2\pi f L_L \)
ただし、実際の計算では出力電圧の式で\(\frac{3}{\pi}X\)の形になるため、\(X = 2\pi f L_L\)を代入すると:
\( \frac{3}{\pi} \times 2\pi f L_L = 6 f L_L \)
このように\(\pi\)が約分されて計算が簡単になります。次のステップで具体的な数値計算を行います。
そうやな!リアクタンス\(X = 2\pi f L_L\)やね。さあ、出力電圧の式に各値を代入してみようか。まずは第1項の\(\frac{3\sqrt{2}}{\pi}V_L\)から計算してみてくれるか?\(V_L = 200\) [V]やで。
第1項\(\frac{3\sqrt{2}}{\pi}V_L\)を計算します。
\(V_L = 200\) [V]を代入すると:
\[ \begin{aligned} \frac{3\sqrt{2}}{\pi} \times V_L &= \frac{3\sqrt{2}}{\pi} \times 200 \\[10pt] &= \frac{3 \times 1.414}{\pi} \times 200 \\[10pt] &= \frac{4.242}{3.14159} \times 200 \\[10pt] &\approx 1.35 \times 200 \\[10pt] &\approx 270.1 \text{ [V]} \end{aligned} \]第1項は約270.1 [V]となります。
ええ計算やな!第1項が270.1 [V]と求まったな。次は第2項の\(\frac{3}{\pi}X \cdot I_d\)を計算してみようか。ここで\(X = 2\pi f L_L\)を代入すると式が簡単になるで。どうなるかな?
第2項\(\frac{3}{\pi}X \cdot I_d\)を計算します。
\(X = 2\pi f L_L\)を代入すると:
\[ \begin{aligned} \frac{3}{\pi}X \cdot I_d &= \frac{3}{\pi} \times 2\pi f L_L \times I_d \\[10pt] &= 6 f L_L \times I_d \end{aligned} \]πが約分されて、式が\(6 f L_L \times I_d\)と簡単になりました。
各値を代入すると:
\[ \begin{aligned} &= 6 \times 50 \times 5.56 \times 10^{-4} \times 36 \\[10pt] &= 6 \times 50 \times 5.56 \times 10^{-4} \times 36 \\[10pt] &\approx 6.005 \text{ [V]} \end{aligned} \]素晴らしい!第2項が約6.005 [V]やな。最後に第3項の\(2V_F\)を計算してみようか。\(V_F = 1.0\) [V]やったな。
第3項\(2V_F\)を計算します。
\(V_F = 1.0\) [V]なので:
\(2V_F = 2 \times 1.0 = 2.0\) [V]
これで全ての項が求まりました:
・第1項:270.1 [V]
・第2項:6.005 [V]
・第3項:2.0 [V]
よっしゃ!全部の項が求まったな。最後に出力電圧\(V_d\)を計算してみようか。式は\(V_d = \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi}X \cdot I_d - 2V_F\)で、各項を代入すると?
出力電圧\(V_d\)を求めます。
各項を代入すると:
\[ \begin{aligned} V_d &= \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi}X \cdot I_d - 2V_F \\[10pt] &= 270.1 - 6.005 - 2.0 \\[10pt] &\approx 262 \text{ [V]} \end{aligned} \]したがって、整流装置の出力電圧は約262 [V]となります。
これは選択肢の(2)に対応します。
完璧や!(b)問題の答えも選択肢の(2)やな!
まとめると、(a)問題ではダイオード1つあたりの損失が12 [W]で選択肢の(1)、(b)問題では出力電圧が262 [V]で選択肢の(2)やったな。三相整流回路では、リアクタンスによる電圧降下とダイオードの順電圧降下が出力電圧を減少させることがポイントやったな!
ありがとうございます!この問題を通して、三相整流装置の特性について理解が深まりました。
重要なポイントをまとめると:
(a)問題について:
・各ダイオードの通電期間は1サイクルの\(\frac{1}{3}\)
・ダイオード1つの平均電流:\(I_D = \frac{I_d}{3} = 12\) [A]
・ダイオード1つの損失:\(P_D = V_F \times I_D = 12\) [W] → 答え:(1)
(b)問題について:
・出力電圧は理想値からリアクタンス降下とダイオード降下を差し引いて求める
・\(V_d = 270.1 - 6.005 - 2.0 = 262\) [V] → 答え:(2)
・リアクタンス\(X = 2\pi f L_L\)により式が簡略化できることも重要なポイントです
解説まとめ
■ 三相整流装置とは
三相整流装置は、三相交流を直流に変換する電力変換装置です。ダイオードを用いた整流回路では、各相の電圧波形に基づいて電流が各ダイオードを順次流れることで直流出力が得られます。実際の回路では、交流側リアクタンスによる電圧降下、ダイオードの順電圧降下などにより理想的な出力電圧より低下します。これらの特性を理解して実際の出力電圧や損失を計算することは、電力変換装置の設計において重要です。
■ 計算手順と公式
- ダイオードの平均電流の計算
三相整流回路では、各ダイオードは1サイクルの1/3の期間だけ導通します。
\( I_D = \frac{1}{3} I_d \)
ここで、IDは1つのダイオードの平均電流[A]、Idは直流電流[A]です。
- ダイオードの損失計算
ダイオードの損失は順電圧降下と平均電流の積で求められます。
\( P_D = V_F \times I_D \)
ここで、PDはダイオードの損失[W]、VFは順電圧降下[V]です。
- リアクタンスの計算
交流側リアクトルのリアクタンスは次式で求められます。
\( X = 2\pi f L_L \)
ここで、Xはリアクタンス[Ω]、fは周波数[Hz]、LLはインダクタンス[H]です。
- 出力電圧の計算
三相整流装置の出力電圧は、理想出力電圧から各種電圧降下を差し引いて求められます。
\( V_d = \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi}X \cdot I_d - 2V_F \)
ここで、Vdは出力電圧[V]、VLは入力線間電圧[V]です。
■ 具体的な計算例
問題条件
- 入力交流電圧: \( V_L = 200 \ \mathrm{[V]} \)
- 周波数: \( f = 50 \ \mathrm{[Hz]} \)
- 直流電流: \( I_d = 36 \ \mathrm{[A]} \)
- 交流側リアクトルのインダクタンス: \( L_L = 5.56 \times 10^{-4} \ \mathrm{[H]} \)
- ダイオードの順電圧降下: \( V_F = 1.0 \ \mathrm{[V]} \)
(a) ダイオードの損失計算
1つのダイオードが通電する期間は1サイクルの1/3であるため、ダイオードの平均電流は:
\[ \begin{aligned} I_D &= \frac{1}{3} I_d \\[5pt] &= \frac{1}{3} \times 36 \\[5pt] &= 12 \ \mathrm{[A]} \end{aligned} \]1つのダイオードで発生する損失は:
\[ \begin{aligned} P_D &= V_F I_D \\[5pt] &= 1.0 \times 12 \\[5pt] &= 12 \ \mathrm{[W]} \end{aligned} \]結論:1つのダイオードで発生する損失は 12 [W] である。(解答:選択肢(1))
(b) 出力電圧の計算
出力電圧の式に各値を代入します:
\[ \begin{aligned} V_d &= \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi}X \cdot I_d - 2V_F \end{aligned} \]リアクタンス \( X = 2\pi f L_L \) を代入して整理します:
\[ \begin{aligned} V_d &= \frac{3\sqrt{2}}{\pi}V_L - \frac{3}{\pi} \cdot 2\pi f L_L \cdot I_d - 2V_F \end{aligned} \]中間項の \( \pi \) が約分されて \( 6f L_L I_d \) となります:
\[ \begin{aligned} V_d &= \frac{3\sqrt{2}}{\pi}V_L - 6 f L_L \cdot I_d - 2V_F \end{aligned} \]各項に数値を代入します:
→ 横スクロールして下さい →
\[ \begin{aligned} V_d &= \frac{3\sqrt{2}}{\pi} \times 200 - 6 \times 50 \times 5.56 \times 10^{-4} \times 36 - 2 \times 1.0 \end{aligned} \]各項を個別に計算すると:
- 第1項(理想出力電圧): \( \frac{3\sqrt{2}}{\pi} \times 200 \approx 270.1 \ \mathrm{[V]} \)
- 第2項(リアクタンスによる電圧降下): \( 6 \times 50 \times 5.56 \times 10^{-4} \times 36 \approx 6.005 \ \mathrm{[V]} \)
- 第3項(ダイオード順電圧降下): \( 2 \times 1.0 = 2 \ \mathrm{[V]} \)
これらを合計して出力電圧を求めます:
\[ \begin{aligned} V_d &\approx 270.1 - 6.005 - 2 \\[5pt] &\approx 262 \ \mathrm{[V]} \end{aligned} \]結論:この整流装置の出力電圧は 262 [V] である。(解答:選択肢(2))
■ 実務上の留意点
三相整流装置の設計と運用における実務上の留意点です。
- ダイオードの発熱による損失は効率低下の原因となるため、適切な冷却設計が必要です。
- 交流側リアクトルは転流リアクトルとも呼ばれ、高調波の抑制効果もありますが、電圧降下による効率低下とのトレードオフがあります。
- 平滑リアクトルは直流電流のリプルを抑制する役割があり、十分に大きな値が必要です。
- 実際の設計では、ダイオードの逆回復時間や温度特性も考慮する必要があります。
- 電源の高調波対策として、入力フィルタや多重化回路の採用が検討されることがあります。
- 負荷変動に対する応答性や制御性を向上させるため、サイリスタを用いた制御整流回路が使用される場合もあります。