【機械】令和6年(下期) 問11|減速機を介した電動機と負荷の回転速度・トルク・出力に関する計算問題
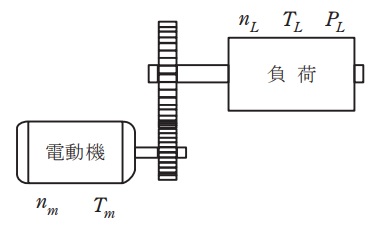
図に示すように,電動機が減速機と組み合わされて負荷を駆動している。このときの電動機の回転速度 \( n_{m} \) が \( 1\,200 \) [min\(^{-1}\)],トルク \( T_{m} \) が \( 100 \) [N·m] であった。
減速機の減速比が \( 6 \),効率が \( 0.96 \) のとき,負荷の回転速度 \( n_{L} \) [min\(^{-1}\)],軸トルク \( T_{L} \) [N·m] 及び軸入力 \( P_{L} \) [kW] の値として,最も近いものを組み合わせたのは次のうちどれか。
 \[
\begin{array}{cccc}
& n_{L} \ [\mathrm{min}^{-1}] & T_{L} \ [\mathrm{N\cdot m}] & P_{L} \ [\mathrm{kW}] \\
\hline
(1) & \ 200 & 16.0 & 12.1 \\
\hline
(2) & \ 200 & 576 \ \ & 12.1 \\
\hline
(3) & 7\,200 & 576 \ \ & 4\,147 \ \ \\
\hline
(4) & 7\,200 & 16.0 & 12.1 \\
\hline
(5) & 7\,200 & 16.0 & 4\,147 \ \ \\
\hline
\end{array}
\]
\[
\begin{array}{cccc}
& n_{L} \ [\mathrm{min}^{-1}] & T_{L} \ [\mathrm{N\cdot m}] & P_{L} \ [\mathrm{kW}] \\
\hline
(1) & \ 200 & 16.0 & 12.1 \\
\hline
(2) & \ 200 & 576 \ \ & 12.1 \\
\hline
(3) & 7\,200 & 576 \ \ & 4\,147 \ \ \\
\hline
(4) & 7\,200 & 16.0 & 12.1 \\
\hline
(5) & 7\,200 & 16.0 & 4\,147 \ \ \\
\hline
\end{array}
\]
合格への方程式
基本概念・仕組み
電動機と減速機って何?
電動機(モーター)は電気エネルギーを回転運動に変換する装置です。でも、電動機だけでは回転が速すぎたり、力(トルク)が足りなかったりすることがあります。そこで**減速機**を組み合わせて使うんです。
減速機の役割
• 高速回転を低速回転に変換
• 小さなトルクを大きなトルクに増幅
• 電動機と負荷の特性をマッチング
身近な例で理解しよう
自転車を思い浮かべてみてください。ペダルをゆっくり回しても、後輪は速く回りますよね?これはチェーンとギアの組み合わせで「増速」しているからです。減速機はこの逆で、**速い回転をゆっくりした強い回転に変える**装置なんです。
具体例:エレベーター
エレベーターでは、電動機が高速で回転しますが、実際のカゴはゆっくり上下します。これは減速機があるからです。高速・低トルクの電動機の回転を、低速・高トルクに変換して重いカゴを安全に動かしているんです。
歯車の基本的な仕組み
減速機の中心は**歯車(ギア)**です。大きな歯車と小さな歯車が噛み合っているとき:
| 歯車の種類 | 回転速度 | トルク | 特徴 |
|---|---|---|---|
| 小さな歯車(電動機側) | 速い | 小さい | 入力側・駆動側 |
| 大きな歯車(負荷側) | 遅い | 大きい | 出力側・被駆動側 |
歯車の基本法則
噛み合う歯車では、**歯の移動距離が等しい**という原理があります。小さな歯車が1回転する間に、大きな歯車は1回転未満しか回りません。この違いが減速比を生み出します。
パワー(動力)の流れ
電動機から減速機、そして負荷へのパワーの流れを理解しましょう:
電動機 → 減速機 → 負荷
• 回転速度:速い → 遅い
• トルク:小さい → 大きい
• パワー:ほぼ同じ(効率分だけ減少)
エネルギー保存の法則
パワー = トルク × 角速度(回転速度)
減速機を通してもパワーは基本的に変わりません(効率損失を除く)。回転速度が半分になれば、トルクは約2倍になります。
減速機の特性と計算
減速比って何?
減速比は**入力側の回転速度を出力側の回転速度で割った値**です。これが減速機の基本特性を決める重要な数値なんです。
\[ \text{減速比} \, a = \frac{n_{\text{入力}}}{n_{\text{出力}}} = \frac{n_m}{n_L} \]減速比の具体例
減速比が6の場合:
• 電動機が6回転すると、負荷は1回転
• 電動機が1200 min⁻¹なら、負荷は200 min⁻¹
• 回転速度は1/6に、トルクは約6倍に
歯車の歯数と減速比の関係
歯車の減速比は歯数の比で決まります:
\[ a = \frac{t_{\text{大きな歯車}}}{t_{\text{小さな歯車}}} = \frac{t_2}{t_1} \]| 小歯車の歯数 | 大歯車の歯数 | 減速比 | 用途例 |
|---|---|---|---|
| 10 | 30 | 3 | 小型送風機 |
| 15 | 90 | 6 | コンベア |
| 20 | 200 | 10 | エレベーター |
| 10 | 500 | 50 | クレーン |
効率の考え方
減速機は完璧ではありません。歯車の摩擦や軸受の損失で、少しだけパワーが失われます。これを**効率**で表します。
\[ \eta = \frac{P_{\text{出力}}}{P_{\text{入力}}} = \frac{P_L}{P_m} \]一般的な減速機の効率
• 歯車減速機:90~98%
• ウォーム減速機:70~95%
• ベルト減速機:95~98%
本問では96%(0.96)を使用
トルクの計算方法
減速機を通すとトルクが増加します。その計算式は:
\[ T_L = \eta \cdot a \cdot T_m \]ここで:
• \( T_L \):負荷側トルク \( \mathrm{[N \cdot m]} \)
• \( T_m \):電動機側トルク \( \mathrm{[N \cdot m]} \)
• \( a \):減速比
• \( \eta \):効率
トルク増加の理由
力のモーメント(てこの原理)と同じです。小さな歯車の半径を ( r_1 )、大きな歯車の半径を ( r_2 ) とすると、同じ力でも ( r_2 ) の方が大きなトルクを生み出せます。減速比 ( a = r_2/r_1 ) なので、理論的にトルクは ( a ) 倍になります。
パワーと回転速度・トルクの関係
パワーの基本式を覚えておきましょう:
\[ P = \omega T = \frac{2\pi n}{60} \cdot T \]ここで:
• \( P \):パワー \( \mathrm{[W]} \)
• \( \omega \):角速度 \( \mathrm{[rad/s]} \)
• \( n \):回転速度 \( \mathrm{[min^{-1}]} \)
• \( T \):トルク \( \mathrm{[N \cdot m]} \)
単位に注意!
• 回転速度の単位:[min⁻¹] or [rpm]
• 角速度の単位:[rad/s]
• 変換式:( \omega = 2\pi n / 60 )
• パワーをkWで求める場合は1000で割る
例題・計算手順
問題設定の整理
まず、与えられた条件を整理しましょう:
与えられた条件
• 電動機回転速度:\( n_m = 1200 \, \mathrm{min^{-1}} \)
• 電動機トルク:\( T_m = 100 \, \mathrm{N \cdot m} \)
• 減速比:\( a = 6 \)
• 効率:\( \eta = 0.96 \)
求めるもの:
• 負荷回転速度:\( n_L \)
• 負荷軸トルク:\( T_L \)
• 負荷軸入力:\( P_L \)
解き方の手順
ステップ1:負荷回転速度を求めよう
減速比の定義から:
\[ a = \frac{n_m}{n_L} \quad \therefore \quad n_L = \frac{n_m}{a} \] \[ n_L = \frac{1200}{6} = 200 \, \text{min}^{-1} \]計算のコツ
減速比が6ということは、電動機が6回転する間に負荷は1回転します。だから電動機の回転速度を6で割ればOKです。
ステップ2:電動機の軸出力を計算しよう
パワーの基本式を使います:
\[ P_m = \frac{2\pi n_m}{60} \cdot T_m \] \[ \begin{aligned} P_m &= \frac{2\pi \times 1200}{60} \times 100 \\[10pt] &= \frac{2400\pi}{60} \times 100 \\[10pt] &= 40\pi \times 100 \\[10pt] &≈ 125.66 \times 100 \\[10pt] &≈ 12566 \, \text{W} = 12.566 \, \text{kW} \end{aligned} \]計算で使う π の値
電験では通常 \( \pi \approx 3.14159 \) または \( 22/7 \) を使います。電卓があれば \( \pi \) キーを使いましょう。手計算なら \( \pi \approx 3.14 \) で十分です。
ステップ3:負荷軸入力を求めよう
効率を考慮します:
\[ P_L = \eta \cdot P_m = 0.96 \times 12.566 ≈ 12.06 \, \text{kW} \]選択肢に合わせて四捨五入すると **12.1 kW** になります。
ステップ4:負荷軸トルクを求めよう
2つの方法があります:
方法1:パワーと回転速度から求める
\[ T_L = \frac{P_L}{\omega_L} = \frac{P_L}{\frac{2\pi n_L}{60}} = \frac{60 P_L}{2\pi n_L} \] \[ \begin{aligned} T_L &= \frac{60 \times 12060}{2\pi \times 200} \\[10pt] &= \frac{723600}{400\pi} \\[10pt] &≈ \frac{723600}{1256.6} \\[10pt] &≈ 576 \, \text{N⋅m} \end{aligned} \]方法2:減速機の特性式から求める
\[ T_L = \eta \cdot a \cdot T_m = 0.96 \times 6 \times 100 = 576 \, \text{N⋅m} \]どちらの方法でも同じ答えが得られることを確認しましょう!
答えの確認
最終答え
• \( n_L = 200 \, \mathrm{min^{-1}} \)
• \( T_L = 576 \, \mathrm{N \cdot m} \)
• \( P_L = 12.1 \, \mathrm{kW} \)
正解:選択肢(2)
計算結果の妥当性チェック
• 回転速度は減速比分だけ下がった ✓
• トルクは減速比×効率倍に増えた ✓
• パワーは効率分だけ減った ✓
物理的に納得できる結果になっています。
応用・実用のポイント
実際の産業での応用例
製造業での活用
| 用途 | 減速比 | 特徴 | 重要なポイント |
|---|---|---|---|
| コンベアベルト | 3~10 | 一定速度運転 | 効率と耐久性 |
| ロボットアーム | 50~200 | 精密位置制御 | バックラッシュ対策 |
| エレベーター | 10~40 | 安全性重視 | ブレーキ機能付き |
| クレーン | 50~500 | 大トルク必要 | 自己保持機能 |
減速機選定の実用ポイント
選定時の検討項目
1. **必要トルク**:負荷に必要なトルクを満足するか
2. **減速比**:所要の回転速度が得られるか
3. **効率**:エネルギー損失は許容範囲か
4. **サイズ・重量**:設置スペースに収まるか
5. **コスト**:初期費用と維持費用のバランス
効率を上げるための工夫
実際の設備では、さらに効率を上げる工夫があります:
効率向上の実用技術
• **潤滑油の最適化**:摩擦を減らして効率向上
• **歯車精度の向上**:加工精度を上げて損失を低減
• **複数段減速**:1段で大きく減速するより効率的
• **軸受の改良**:転がり軸受で摩擦損失を最小化
トラブルシューティング
よくある問題と対策
異音・振動の原因
• 歯車の摩耗:定期的な点検とメンテナンス
• アライメント不良:据付時の精度管理
• 潤滑不良:適切な潤滑油の補給・交換
• 過負荷運転:定格範囲内での使用
効率低下の要因
| 要因 | 対策 | 効果 |
|---|---|---|
| 潤滑油劣化 | 定期交換 | 効率2~5%向上 |
| 軸受摩耗 | 早期交換 | 振動・騒音減少 |
| 歯車摩耗 | 適正負荷運転 | 寿命延長 |
| 温度上昇 | 冷却改善 | 効率維持 |
省エネ運転のコツ
エネルギー効率を最大化する方法
• **適正負荷での運転**:定格の70~90%が最も効率的
• **インバータ制御**:負荷に応じた回転数制御
• **定期メンテナンス**:性能維持で効率低下を防止
• **温度管理**:適正温度での運転で損失を最小化
最新技術動向
IoT・スマート化の活用
現代の減速機には、以下のような最新技術が導入されています:
Industry 4.0対応減速機
• **状態監視システム**:振動・温度・電流を常時監視
• **予知保全**:AIによる故障予測で計画的メンテナンス
• **リモート診断**:遠隔地からの状態確認・設定変更
• **エネルギー可視化**:効率の見える化で省エネ促進
環境対応技術
持続可能な社会に向けた取り組みも進んでいます:
• **高効率設計**:IE4クラスモータとの組み合わせ
• **長寿命化**:メンテナンスフリー設計
• **リサイクル対応**:解体しやすい構造設計
• **省資源化**:小型軽量化による材料使用量削減
電験三種への応用
減速機の計算問題は、電気機器の効率計算や電力計算の基礎となります。機械と電気の境界領域として、実務でも重要な知識です。しっかりと理解して、応用問題にも対応できるようにしましょう。
🔍 ワンポイントアドバイス: 減速機の問題では「減速比」「効率」「パワー保存則」の3つがキーポイントです。図を見ながら、どの値がどこに対応するかを整理してから計算に入ると間違いが減ります。また、実際の電気設備では減速機は非常によく使われるので、仕組みを理解しておくと実務でも役立ちますよ!
よっしゃ、今度は電動機と減速機の組み合わせ問題やな!これは機械科目でよく出る問題で、電動機単体の計算とはちょっと違うから、最初は戸惑うかもしれんけど、基本的な考え方を理解すれば必ず解けるようになるで。まずは図を見ながら、どんなシステムになってるか確認してみよか!
はい、先生!図を見ながらシステムを理解いたします。
【システムの構成】
電動機 → 減速機 → 負荷 の順で動力が伝達されています。
【与えられた条件】
・電動機の回転速度:\( n_m = 1200 \, \mathrm{[min^{-1}]} \)
・電動機のトルク:\( T_m = 100 \, \mathrm{[N \cdot m]} \)
・減速比:6
・減速機の効率:\( \eta = 0.96 \)
【求めるもの】
・負荷の回転速度:\( n_L \, \mathrm{[min^{-1}]} \)
・負荷の軸トルク:\( T_L \, \mathrm{[N \cdot m]} \)
・負荷の軸入力:\( P_L \, \mathrm{[kW]} \)
【システムの動作原理】
電動機が高速・低トルクで回転し、減速機によって低速・高トルクに変換されて負荷を駆動するシステムです。日常生活では自動車のトランスミッションのような役割ですね。
そうそう、システムの理解はバッチリやな!減速機っていうのは、文字通り回転を遅くする(減速する)代わりに、トルクを大きくする装置なんや。これは「動力の保存」っていう大事な原理に基づいてるんやで。まず最初に、減速比の概念から理解していこうか。減速比が6っていうのは、どういう意味か分かるかな?
はい!減速比について説明いたします。
【減速比の意味】
減速比が6ということは:
つまり、電動機が6回転する間に、負荷は1回転するということです。
【歯車での考え方】
歯車で考えると、小さな歯車(電動機側)が大きな歯車(負荷側)を回すとき:
・小歯車の歯数:\( t_1 \)
・大歯車の歯数:\( t_2 \)
・減速比:\( a = \frac{t_2}{t_1} = \frac{n_m}{n_L} = 6 \)
【物理的意味】
・電動機は高速で回転するが、トルクは比較的小さい
・減速機を通すことで、回転速度は1/6になるが、トルクは理論的には6倍になる
・実際には効率があるため、トルクは6倍×効率となる
このように、減速比は回転速度とトルクの変換比を表す重要な値なのです。
完璧や!減速比の理解もバッチリやな。ほんで、まず最初に計算するのは負荷の回転速度 \( n_L \) やで。これは減速比の関係から簡単に求められるんや。電動機の回転速度が1200 [min⁻¹]で、減速比が6やから、どうなるか計算してみてな!
はい!負荷の回転速度 \( n_L \) を計算いたします。
【負荷の回転速度の計算】
減速比の関係式:
\[ \text{減速比} = \frac{n_m}{n_L} = 6 \]これを \( n_L \) について解くと:
\[ \begin{aligned} n_L &= \frac{n_m}{\text{減速比}} \\[10pt] &= \frac{1200}{6} \\[10pt] &= 200 \, \mathrm{[min^{-1}]} \end{aligned} \]【結果の確認】
電動機が1200回転/分で回っているとき、負荷は200回転/分で回転します。
確認:\( \frac{1200}{200} = 6 \) ✓(減速比と一致)
【物理的イメージ】
電動機が6回転する間に、負荷が1回転するという関係が正しく計算できました。これで選択肢を見ると、\( n_L = 200 \) の選択肢は(1)と(2)に絞られますね。
その通り!負荷の回転速度は200 [min⁻¹]で正解や。選択肢も(1)と(2)に絞られたな。ほんで次は、電動機の軸出力 \( P_m \) を計算するんや。出力は「トルク×角速度」で計算できるけど、角速度に変換するときの公式、覚えてるかな?前回の問題でも使ったやつや!
はい!覚えています。電動機の軸出力を計算いたします。
【電動機の軸出力の計算】
出力とトルク、角速度の関係:
\[ P_m = \omega_m T_m \]回転速度[min⁻¹]から角速度[rad/s]への変換:
\[ \omega_m = \frac{2\pi n_m}{60} \]与えられた値を代入:
・\( n_m = 1200 \, \mathrm{[min^{-1}]} \)
・\( T_m = 100 \, \mathrm{[N \cdot m]} \)
したがって、電動機の軸出力は約 \( 12.57 \, \mathrm{[kW]} \) です。
完璧や!電動機の軸出力も正確に計算できたな。ほんで次は、減速機の効率を考慮して負荷の軸入力 \( P_L \) を求めるんや。減速機っていうのは、動力を伝達するときに摩擦とかで少しエネルギーを失うから、効率が1.0より小さくなるんやで。効率0.96っていうことは、96%のエネルギーが負荷に伝わるってことや。計算してみよか!
はい!減速機の効率を考慮して負荷の軸入力を計算いたします。
【負荷の軸入力の計算】
減速機の効率の関係式:
\[ P_L = \eta P_m \]ここで:
・\( P_L \):負荷の軸入力(減速機の出力)[kW]
・\( \eta \):減速機の効率 = 0.96
・\( P_m \):電動機の軸出力(減速機の入力)= 12.566 [kW]
【エネルギー損失の理解】
・電動機からの出力:12.57 kW
・負荷への入力:12.1 kW
・減速機での損失:12.57 - 12.1 = 0.47 kW(約4%の損失)
これで選択肢を確認すると、\( n_L = 200 \) かつ \( P_L = 12.1 \) なので、(1)または(2)のどちらかです。残るは軸トルク \( T_L \) の計算ですね!
ばっちりやな!軸入力も正確に計算できて、選択肢もだいぶ絞れたな。ほんで最後は負荷の軸トルク \( T_L \) を求めるんや。これは少し考え方があるんやけど、今求めた負荷の軸入力 \( P_L \) と負荷の回転速度 \( n_L \) から、「出力=トルク×角速度」の関係を使って逆算するんやで。やってみよか!
はい!負荷の軸トルク \( T_L \) を計算いたします。
【負荷の軸トルクの計算】
出力とトルクの関係式:
\[ P_L = \omega_L T_L \]これを \( T_L \) について解くと:
\[ T_L = \frac{P_L}{\omega_L} \]まず、負荷の角速度 \( \omega_L \) を計算:
\[ \begin{aligned} \omega_L &= \frac{2\pi n_L}{60} \\[10pt] &= \frac{2\pi \times 200}{60} \\[10pt] &= \frac{400\pi}{60} \\[10pt] &= \frac{20\pi}{3} \\[10pt] &\approx 20.94 \, \mathrm{[rad/s]} \end{aligned} \]次に、軸トルクを計算:
\[ \begin{aligned} T_L &= \frac{P_L}{\omega_L} \\[10pt] &= \frac{12.063 \times 10^3}{20.94} \\[10pt] &= \frac{12063}{20.94} \\[10pt] &\approx 576 \, \mathrm{[N \cdot m]} \end{aligned} \]したがって、負荷の軸トルクは約 \( 576 \, \mathrm{[N \cdot m]} \) です。
素晴らしい!完璧な計算やな。ほんで結果をまとめると、\( n_L = 200 \)、\( T_L = 576 \)、\( P_L = 12.1 \) になったわけや。選択肢を見ると、これは明らかに(2)番やな!でも、ここで一つ確認しておきたいことがあるんや。今回求めたトルクが576 [N⋅m]で、元の電動機のトルクが100 [N⋅m]やったけど、この関係どう思う?
はい!トルクの関係について考察いたします。
【計算結果のまとめ】
・負荷の回転速度:\( n_L = 200 \, \mathrm{[min^{-1}]} \)
・負荷の軸トルク:\( T_L = 576 \, \mathrm{[N \cdot m]} \)
・負荷の軸入力:\( P_L = 12.1 \, \mathrm{[kW]} \)
したがって、答えは (2) です。
【トルクの関係の考察】
・電動機のトルク:\( T_m = 100 \, \mathrm{[N \cdot m]} \)
・負荷のトルク:\( T_L = 576 \, \mathrm{[N \cdot m]} \)
・トルク比:\( \frac{T_L}{T_m} = \frac{576}{100} = 5.76 \)
【理論値との比較】
効率を考慮しない場合のトルク比 = 減速比 = 6
実際のトルク比 = 減速比 × 効率 = 6 × 0.96 = 5.76 ✓
この結果は理論的に正しいです!減速機により:
・回転速度は1/6に減少(1200 → 200)
・トルクは約5.76倍に増加(100 → 576)
・効率のため、トルク増加は減速比×効率となる
まさに「減速機の動力変換」が正しく計算できていることが確認できました!
完璧や!トルクの関係まで理論的に確認してくれて、めっちゃええ感じやな。ほんで、この問題を解く上でのもう一つの重要なポイントを確認しておこうか。実は、負荷のトルクを求める方法は今回使った方法以外にもあるんや。減速機の理論から直接計算する方法もあるんやで。どんな方法か分かるかな?
はい!減速機の理論から直接トルクを計算する方法について説明いたします。
【減速機のトルク関係式】
減速機におけるトルクの関係は、効率を考慮すると:
\[ T_L = \eta \times \text{減速比} \times T_m \]【直接計算による検証】
\[ \begin{aligned} T_L &= \eta \times a \times T_m \\[10pt] &= 0.96 \times 6 \times 100 \\[10pt] &= 5.76 \times 100 \\[10pt] &= 576 \, \mathrm{[N \cdot m]} \end{aligned} \]【2つの計算方法の比較】
方法1: 出力から逆算(今回使用)
\( P_L → \omega_L → T_L = \frac{P_L}{\omega_L} \)
方法2: 減速機の理論式(直接計算)
\( T_L = \eta \times a \times T_m \)
両方とも同じ結果(576 N⋅m)になることが確認できました!
【使い分けのポイント】
・方法1:出力が重要な場合、エネルギーの流れを把握したい場合
・方法2:トルクの変換だけを知りたい場合、計算が簡単
素晴らしい!2つの方法でちゃんと同じ答えが出ることを確認してくれたな。これで計算の信頼性もバッチリや。ほんで、この問題を解く上で重要な「間違いやすいポイント」について確認しておこうか。特に、回転速度とトルクの関係で、受験生がよく混乱するところがあるんや。どんな間違いが起こりやすいと思う?
はい!この問題でよくある間違いパターンについて分析いたします。
【よくある間違いパターン】
1. 減速比の適用方向の間違い
❌ 間違い:\( n_L = n_m \times 6 = 7200 \)
✅ 正解:\( n_L = \frac{n_m}{6} = 200 \)
→ 選択肢(3)(4)(5)は7200なので、この間違いを狙った引っかけ
2. トルクの増減方向の混乱
❌ 間違い:「減速機だからトルクも減る」と勘違い
✅ 正解:減速機は回転数を減らし、トルクを増やす装置
→ 選択肢(1)(4)(5)の16.0は、トルクが減ると間違って考えた場合
3. 効率の考慮忘れ
❌ 間違い:\( T_L = 6 \times 100 = 600 \)
✅ 正解:\( T_L = 0.96 \times 6 \times 100 = 576 \)
→ 効率を忘れると600になってしまう
4. 出力計算での単位間違い
❌ 間違い:角速度の計算で60を掛けてしまう
✅ 正解:[min⁻¹]→[rad/s]は60で割る
→ 選択肢(3)(5)の4147は、このような計算ミスから生じる可能性
【確実に解くための対策】
・減速機は「高速低トルク → 低速高トルク」の変換装置と覚える
・効率は必ず1未満で、出力とトルクの両方に影響する
・単位変換は慎重に行う
完璧やな!よくある間違いパターンもしっかり分析してくれて、選択肢の意図まで理解してくれたのは素晴らしいで。最後に、この減速機の問題が実際の現場でどんなふうに活用されるのか、そして今回学んだ計算方法がどう役立つのか考えてみよか。現場での応用例、何か思い浮かぶかな?
はい!減速機の現場での応用と今回の計算方法の実用性について考察いたします。
【現場での減速機の応用例】
1. 産業機械
・コンベヤベルト:高速モーターを減速してベルトを適切な速度で駆動
・クレーン:重い荷物を持ち上げるため、高トルクが必要
・工作機械:精密な送り速度制御のため
2. 建設機械
・ショベルカー:旋回機構や走行機構
・ミキサー車:ドラムを適切な回転数で回すため
3. 発電・送電設備
・風力発電:風車の低速回転を発電機の高速回転に変換(増速機)
・水力発電:水車の回転を発電機に適した回転数に調整
【今回の計算方法の実用性】
1. 設備設計時
・必要なトルクと回転数から適切な減速比を決定
・電動機の容量選定
・システム全体の効率計算
2. 保守・点検時
・減速機の効率測定による劣化診断
・異常振動や異音の原因究明
・負荷の変化による影響評価
3. 省エネルギー対策
・最適な運転条件の決定
・インバータ制御との組み合わせ
・エネルギー損失の最小化
電験三種の知識が、実際の電気設備の運用に直結していることがよく分かりますね!
解説まとめ
■ 電動機と減速機の組み合わせとは
電動機の高速回転を減速機により減速して負荷を駆動するシステムは、産業機械で広く使用されています。減速機は歯車機構により回転速度を下げる一方でトルクを増大させ、負荷に適した駆動条件を実現します。このとき、減速比、効率、動力の関係を理解することが重要です。回転速度は減速比に反比例し、トルクは減速比と効率に比例して増大します。
■ 計算手順と公式
- 減速比による回転速度の関係
減速比aのとき、負荷側の回転速度は電動機側の1/a倍になります。
\( n_L = \frac{n_m}{a} \)
- 電動機の軸出力の計算
角速度とトルクの積から軸出力を求めます。
\( P_m = \omega_m T_m = \frac{2\pi n_m}{60} \cdot T_m \)
- 減速機の効率を考慮した負荷側入力
減速機での損失を考慮し、負荷側の軸入力を計算します。
\( P_L = \eta P_m \)
- 負荷側トルクの計算
負荷側の軸入力と角速度から軸トルクを求めます。
\( T_L = \frac{P_L}{\omega_L} = \frac{60 P_L}{2\pi n_L} \)
■ 具体的な計算例
問題条件
- 電動機の回転速度:\( n_m = 1200 \) min⁻¹
- 電動機のトルク:\( T_m = 100 \) N·m
- 減速機の減速比:\( a = 6 \)
- 減速機の効率:\( \eta = 0.96 \)
負荷の回転速度の計算
\[ \begin{aligned} n_L &= \frac{n_m}{a} \\[5pt] &= \frac{1200}{6} \\[5pt] &= 200 \ \mathrm{[min^{-1}]} \end{aligned} \]電動機の軸出力の計算
\[ \begin{aligned} P_m &= \frac{2\pi n_m}{60} \cdot T_m \\[5pt] &= \frac{2\pi \times 1200}{60} \times 100 \\[5pt] &= 40\pi \times 100 \\[5pt] &\approx 12570 \ \mathrm{[W]} = 12.57 \ \mathrm{[kW]} \end{aligned} \]負荷の軸入力の計算
\[ \begin{aligned} P_L &= \eta P_m \\[5pt] &= 0.96 \times 12.57 \\[5pt] &\approx 12.07 \ \mathrm{[kW]} \\[5pt] &\approx 12.1 \ \mathrm{[kW]} \end{aligned} \]負荷の軸トルクの計算
\[ \begin{aligned} T_L &= \frac{60 P_L}{2\pi n_L} \\[5pt] &= \frac{60 \times 12.07 \times 10^3}{2\pi \times 200} \\[5pt] &= \frac{724200}{400\pi} \\[5pt] &\approx 576 \ \mathrm{[N \cdot m]} \end{aligned} \]結論:\( n_L = 200 \) min⁻¹、\( T_L = 576 \) N·m、\( P_L = 12.1 \) kW となり、選択肢 (2) が正解です。
■ 実務上の留意点
電動機と減速機を組み合わせたシステムの設計・運用では、以下の点に注意が必要です。
- 減速比を大きくすると、トルクは増大しますが、減速機のサイズも大きくなり、効率も低下する傾向があります。
- 減速機の効率は一般的に90~98%程度で、歯車の種類や精度、潤滑状態により変化します。
- 電動機の選定では、負荷の必要トルクを減速比で除した値以上のトルクが必要です。
- 慣性モーメントの影響も考慮し、起動時や加減速時の特性も検討する必要があります。
- 実際の設計では、安全率を考慮して電動機容量に余裕を持たせることが一般的です。