【機械】平成24年 問4|三相誘導電動機における滑りと巻線抵抗を考慮した効率の計算問題
三相誘導電動機があり,一次巻線抵抗が \( 15 \) [\(\Omega\)],一次側に換算した二次巻線抵抗が \( 9 \) [\(\Omega\)],滑りが \( 0.1 \) のとき,効率 (%) の値として,最も近いものを次の (1)~(5) のうちから一つ選べ。
ただし,励磁電流は無視できるものとし,損失は,一次巻線による銅損と二次巻線による銅損しか存在しないものとする。
合格への方程式
誘導電動機のL形等価回路
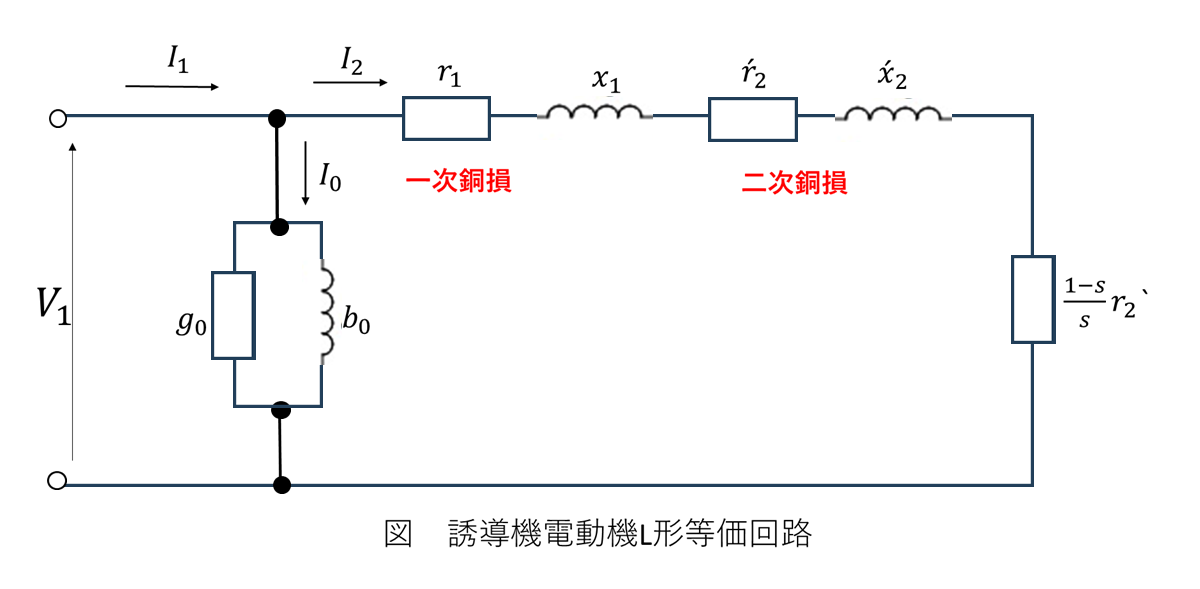
誘導電動機のL形等価回路は、三相誘導電動機の特性を理解・計算するための基本となる回路です。この回路モデルにより、電動機の挙動を電気回路として解析できます。
L形等価回路の主要パラメータ
\(\dot{V}_1 \; [\mathrm{V}]\):一次側端子電圧
\(\dot{I}_1 \; [\mathrm{A}]\):一次電流
\(\dot{I}_2 \; [\mathrm{A}]\):二次電流
\(\dot{I}_0 \; [\mathrm{A}]\):励磁電流
\(r_1 \; [\Omega]\):一次巻線抵抗
\(r_2' \; [\Omega]\):二次巻線抵抗(一次換算値)
\(x_1 \; [\Omega]\):一次漏れリアクタンス
\(x_2' \; [\Omega]\):二次漏れリアクタンス(一次換算値)
\(s\):滑り(0〜1の値)
等価回路の意味するもの
L形等価回路は、実際の三相誘導電動機を電気的な素子(抵抗やリアクタンス)で表現したモデルです。この回路を理解することで、電圧や電流から電動機の出力やトルクなどの特性を計算できるようになります。
電動機の特性を左右する重要な要素が「滑り \(s\)」です。これは回転子の回転速度と同期速度の差を表す指標で、負荷が大きくなるほど滑りも大きくなります。
等価回路から見る動作状態
・滑り \(s = 0\) のとき:無負荷状態(理想的には同期速度で回転)
・滑り \(s = 1\) のとき:拘束状態(始動時や過負荷で回転子が停止)
・通常運転時:\(s\) は約0.01〜0.05程度(負荷により変動)
滑りと出力の関係
誘導電動機の特性を理解する上で、滑り \(s\) と各種電力(入力・出力・損失)の関係は非常に重要です。
同期速度と滑りの定義
同期速度 \(n_0 \; [\mathrm{r/min}]\) は電源周波数 \(f \; [\mathrm{Hz}]\) と極数 \(P\) から決まります:
\[ n_0 = \frac{120f}{P} \; [\mathrm{r/min}] \]
滑り \(s\) は回転子の実際の回転速度 \(n \; [\mathrm{r/min}]\) と同期速度 \(n_0 \; [\mathrm{r/min}]\) の差の比で定義されます:
\[ s = \frac{n_0 - n}{n_0} \]
二次入力・出力・二次銅損の関係
L形等価回路から、以下の電力の関係式が導かれます:
\[ \begin{aligned} P_{\mathrm{o}} &= 3\frac{1-s}{s}r_2'I_2^2 \; [\mathrm{W}] \\[10pt] P_{\mathrm{c2}} &= 3r_2'I_2^2 \; [\mathrm{W}] \\[10pt] P_{2} &= P_{\mathrm{o}}+P_{\mathrm{c2}} = 3\frac{r_2'}{s}I_2^2 \; [\mathrm{W}] \end{aligned} \]
これらの関係から、以下の重要な比率が導き出されます:
\[ P_{2} : P_{\mathrm{o}} : P_{\mathrm{c2}} = 1 : (1-s) : s \]
計算例
滑り \(s = 0.04\) の場合、二次入力 \(P_2\)、出力 \(P_{\mathrm{o}}\)、二次銅損 \(P_{\mathrm{c2}}\) の比率は:
\[ \begin{aligned} P_{2} : P_{\mathrm{o}} : P_{\mathrm{c2}} &= 1 : (1-0.04) : 0.04 \\[10pt] &= 1 : 0.96 : 0.04 \end{aligned} \]
つまり、二次入力の96%が機械的出力となり、4%が二次銅損となります。
物理的意味
滑りの値が小さいほど、二次入力のうち機械的出力に変換される割合が大きくなり、効率が向上します。逆に滑りが大きいと二次銅損の割合が増加し、効率が低下します。この関係から、効率の良い運転状態では滑りを小さく保つことが重要だと分かります。
効率と損失
誘導電動機の効率は、入力電力に対する出力電力の比率で定義されます。効率を考える際には、様々な損失要素を理解する必要があります。
三相誘導電動機の電力フロー
| 項目 | 記号 | 説明 |
|---|---|---|
| 一次入力 | \(P_{\mathrm{1}} \; [\mathrm{W}]\) | 電源から供給される電力 |
| 二次入力 | \(P_{2} \; [\mathrm{W}]\) | 一次から二次に伝達される電力 |
| 出力 | \(P_{\mathrm{o}} \; [\mathrm{W}]\) | 機械的出力(軸出力) |
| 鉄損 | \(P_{\mathrm{i}} \; [\mathrm{W}]\) | ヒステリシス損・渦電流損 |
| 一次銅損 | \(P_{\mathrm{c1}} \; [\mathrm{W}]\) | 固定子巻線での抵抗損失 |
| 二次銅損 | \(P_{\mathrm{c2}} \; [\mathrm{W}]\) | 回転子巻線での抵抗損失 |
電力の関係式
\[ \begin{aligned} P_{\mathrm{2}} &= P_{\mathrm{1}} - P_{\mathrm{i}} - P_{\mathrm{c1}} \\[10pt] P_{\mathrm{o}} &= P_{\mathrm{2}} - P_{\mathrm{c2}} \\[10pt] &= P_{\mathrm{1}} - P_{\mathrm{i}} - P_{\mathrm{c1}} - P_{\mathrm{c2}} \end{aligned} \]
効率 \(\eta\) は以下のように定義されます:
\[ \begin{aligned} \eta &= \frac{P_{\mathrm{o}}}{P_{\mathrm{1}}} \times 100 \; [\%] \\[10pt] &= \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + P_{\mathrm{i}} + P_{\mathrm{c1}} + P_{\mathrm{c2}}} \times 100 \; [\%] \end{aligned} \]
損失の特徴
各損失の特徴と負荷との関係は以下のようになります:
・鉄損 \(P_{\mathrm{i}}\):主に電圧と周波数に依存し、負荷にあまり影響されない
・一次銅損 \(P_{\mathrm{c1}}\):一次電流の二乗に比例するため、負荷が大きくなると増加
・二次銅損 \(P_{\mathrm{c2}}\):二次電流の二乗と滑りに比例するため、負荷が大きくなると増加
効率計算例
一次入力 \(P_1 = 10 \; \mathrm{kW}\)、鉄損 \(P_{\mathrm{i}} = 300 \; \mathrm{W}\)、一次銅損 \(P_{\mathrm{c1}} = 400 \; \mathrm{W}\)、二次銅損 \(P_{\mathrm{c2}} = 350 \; \mathrm{W}\) の場合:
\[ \begin{aligned} P_{\mathrm{o}} &= P_1 - P_{\mathrm{i}} - P_{\mathrm{c1}} - P_{\mathrm{c2}} \\[10pt] &= 10000 - 300 - 400 - 350 \\[10pt] &= 8950 \; \mathrm{W} \\[10pt] \eta &= \frac{8950}{10000} \times 100 = 89.5 \; \% \end{aligned} \]
注意点
上記の損失以外にも、機械損(軸受摩擦損・風損)や漂遊負荷損など、実際の電動機では様々な損失が発生します。しかし、L形等価回路モデルでは主に電気的な損失に焦点を当てています。
トルク特性と計算
誘導電動機のトルク特性は、負荷に対する応答性を示す重要な指標です。L形等価回路を用いて、トルクを計算・予測することができます。
トルクの基本式
誘導電動機の発生トルク \(T \; [\mathrm{N \cdot m}]\) は、出力 \(P_{\mathrm{o}} \; [\mathrm{W}]\) と角速度 \(\omega \; [\mathrm{rad/s}]\) の関係から:
\[ T = \frac{P_{\mathrm{o}}}{\omega} = \frac{P_{\mathrm{o}}}{2\pi n/60} = \frac{60}{2\pi} \cdot \frac{P_{\mathrm{o}}}{n} \; [\mathrm{N \cdot m}] \]
ここで、\(n \; [\mathrm{r/min}]\) は回転速度です。
L形等価回路の関係式を用いると、トルクは以下のように表せます:
\[ \begin{aligned} T &= \frac{60}{2\pi} \cdot \frac{P_{\mathrm{o}}}{n} \\[10pt] &= \frac{60}{2\pi} \cdot \frac{3\frac{1-s}{s}r_2'I_2^2}{n_0(1-s)} \\[10pt] &= \frac{60}{2\pi} \cdot \frac{3r_2'I_2^2}{s \cdot n_0} \\[10pt] &= \frac{9.55 \cdot 3r_2'I_2^2}{s \cdot n_0} \; [\mathrm{N \cdot m}] \end{aligned} \]
最大トルクの条件
誘導電動機のトルクが最大となる滑り \(s_m\) は以下の式で求められます:
\[ s_m = \frac{r_2'}{\sqrt{r_1^2 + (x_1 + x_2')^2}} \]
最大トルク \(T_{max}\) は以下のように表されます:
\[ T_{max} = \frac{3V_1^2}{2\omega_0[r_1 + \sqrt{r_1^2 + (x_1 + x_2')^2}]} \; [\mathrm{N \cdot m}] \]
ここで、\(\omega_0 = 2\pi f\) は同期角速度です。
トルク-滑り特性曲線
誘導電動機のトルク \(T\) と滑り \(s\) の関係は、以下の特徴を持ちます:
・始動時(\(s = 1\)):始動トルク \(T_s\) が発生
・最大トルク点(\(s = s_m\)):最大トルク \(T_{max}\) が発生
・定格運転時(\(s = s_N\)):定格トルク \(T_N\) が発生
通常、\(s_m\) は\(s_N\)より大きい値になるように設計されています(\(s_m > s_N\))。これにより、負荷が増加しても安定した運転が可能になります。
トルク計算例
二次電流 \(I_2 = 10 \; \mathrm{A}\)、二次巻線抵抗(一次換算値) \(r_2' = 0.5 \; \Omega\)、滑り \(s = 0.05\)、同期速度 \(n_0 = 1500 \; \mathrm{r/min}\) の場合のトルク:
\[ \begin{aligned} T &= \frac{9.55 \cdot 3 \cdot 0.5 \cdot 10^2}{0.05 \cdot 1500} \\[10pt] &= \frac{9.55 \cdot 3 \cdot 0.5 \cdot 100}{75} \\[10pt] &= \frac{9.55 \cdot 150}{75} \\[10pt] &= 19.1 \; \mathrm{N \cdot m} \end{aligned} \]
速度制御方法
三相誘導電動機の速度制御は、様々な産業応用において重要な要素です。L形等価回路の理解を基に、速度制御の原理とその特徴を見ていきましょう。
回転速度の基本式
誘導電動機の回転速度 \(n \; [\mathrm{r/min}]\) は、同期速度 \(n_0 \; [\mathrm{r/min}]\) と滑り \(s\) を用いて以下のように表されます:
\[ n = n_0(1-s) = \frac{120f}{P}(1-s) \; [\mathrm{r/min}] \]
この式から、速度制御には以下の3つの方法があることがわかります:
1. 極数 \(P\) の変更
2. 周波数 \(f\) の制御
3. 滑り \(s\) の調整
主な速度制御方法
| 制御方法 | 原理 | 特徴 |
|---|---|---|
| 極数変換法 | 固定子巻線の極数を切り替える | 段階的な速度制御(2速、4速など)が可能 |
| インバータ制御 (V/f一定制御) |
電源周波数と電圧を同時に制御 | 広範囲の連続的な速度制御が可能 高効率で省エネルギー |
| 二次抵抗制御 | 巻線形誘導電動機の二次抵抗を可変 | 始動特性の改善 低速域での制御に有効 |
| ベクトル制御 | 磁束と電流のベクトル関係を制御 | 高応答・高精度な速度制御が可能 DCモータに近い制御性能 |
インバータ制御の原理
インバータ制御(V/f一定制御)は、電圧 \(V\) と周波数 \(f\) の比を一定に保ちながら制御します。これにより、広い範囲で磁束を一定に保ち、効率の良い運転が可能になります。
L形等価回路から考えると、周波数 \(f\) を変えると同期速度 \(n_0\) が変わり、電圧 \(V\) を適切に制御することで磁束(\(\dot{I}_0\))を一定に保ちます。これにより、トルク特性を維持したまま速度を制御できます。
速度制御の計算例
極数 \(P = 4\)、定格周波数 \(f = 50 \; \mathrm{Hz}\)、定格滑り \(s = 0.04\) の誘導電動機の場合:
定格速度:
\[ \begin{aligned} n &= \frac{120 \cdot 50}{4}(1-0.04) \\[10pt] &= 1500 \cdot 0.96 = 1440 \; \mathrm{r/min} \end{aligned} \]
インバータで周波数を \(f = 30 \; \mathrm{Hz}\) に変更した場合(滑りは同じと仮定):
\[ \begin{aligned} n &= \frac{120 \cdot 30}{4}(1-0.04) \\[10pt] &= 900 \cdot 0.96 = 864 \; \mathrm{r/min} \end{aligned} \]
速度制御時の注意点
・低周波数域での制御:V/f一定制御では、低周波数域で電圧降下の影響が大きくなるため、電圧のブースト(補償)が必要
・高周波数域での制御:電源電圧以上に出力電圧を上げられないため、定出力領域での制御となる(弱め界磁制御)
・温度上昇:長時間の低速運転では冷却効果が低下するため、温度上昇に注意が必要
🔍 ワンポイントアドバイス: 三相誘導電動機の試験問題では、L形等価回路から出力、効率、トルクなどを計算する問題がよく出題されます。特に「二次入力:出力:二次銅損 = 1:(1-s):s」の関係式は重要な出題ポイントです。また、滑りと最大トルクの関係、速度制御方法の特徴と適用例についても押さえておきましょう。モータの特性曲線(トルク-速度特性など)をグラフのイメージとして理解しておくと、問題解決の助けになります。
おっ、今日は三相誘導電動機のL形等価回路について勉強するんやな!まずはこの図を見てみ!

この回路図は三相誘導電動機のL形等価回路っちゅうんや。ここでは励磁回路に電流が流れへんから、\( I_0 = 0 \)、\( I_1 = I_2 = I \)という条件で考えるで。まずは電動機の出力パワー \( P_{\mathrm{o}} \) について考えてみようか?
はい、先生!三相誘導電動機の出力パワー \( P_{\mathrm{o}} \) は、滑り率とトルクに関係があると思います。二次側の抵抗と電流から求められますよね?
そやそや!よう知ってるな!三相誘導電動機の出力パワー \( P_{\mathrm{o}} \) は二次側の抵抗と電流、そして滑り率から計算できるんや。式で表すとこうなるで:
\( P_{\mathrm{o}} = 3 \cdot \frac{1-s}{s} \cdot {r_2}' \cdot I^2 \)
ここで \( s \) は滑り率、\( {r_2}' \) は二次側抵抗や。この問題では \( s = 0.1 \)、\( {r_2}' = 9 \) が与えられてるから、これを式に代入してみ?
はい、先生!与えられた値を代入して計算します。
\[ \begin{aligned} P_{\mathrm{o}} &= 3 \cdot \frac{1-s}{s} \cdot {r_2}' \cdot I^2 \\ &= 3 \times \frac{1-0.1}{0.1} \times 9 \times I^2 \\ &= 3 \times \frac{0.9}{0.1} \times 9 \times I^2 \\ &= 3 \times 9 \times 9 \times I^2 \\ &= 243I^2 \end{aligned} \]出力パワーは \( P_{\mathrm{o}} = 243I^2 \) となりました!
ええやん!次は一次銅損 \( P_{\mathrm{c1}} \) について考えるで。銅損ちゅうんは電流が導体(銅線)を流れるときに発生する損失のことやな。一次側の銅損はどう表せると思う?
はい!一次銅損 \( P_{\mathrm{c1}} \) は一次側の抵抗 \( r_1 \) と電流 \( I \) の二乗に比例すると思います。三相なので3倍して...
\( P_{\mathrm{c1}} = 3 \cdot r_1 \cdot I^2 \)
と表せます。図から \( r_1 = 15 \) ですので:
\[ \begin{aligned} P_{\mathrm{c1}} &= 3 \times r_1 \times I^2 \\ &= 3 \times 15 \times I^2 \\ &= 45I^2 \end{aligned} \]一次銅損は \( P_{\mathrm{c1}} = 45I^2 \) になります。
ほんまよう理解してるやん!次は二次銅損 \( P_{\mathrm{c2}} \) や。これも同じように考えられるやろ?二次側の抵抗 \( {r_2}' \) を使って表してみて。
はい、先生!二次銅損も同じ考え方で求められますね。二次側の抵抗 \( {r_2}' \) と電流 \( I \) から:
\[ \begin{aligned} P_{\mathrm{c2}} &= 3 \times {r_2}' \times I^2 \\ &= 3 \times 9 \times I^2 \\ &= 27I^2 \end{aligned} \]二次銅損は \( P_{\mathrm{c2}} = 27I^2 \) となりました。
ようできてるわ!これで出力パワーと損失が全部求まったな。さて、こんな感じになってるで:
出力パワー: \( P_{\mathrm{o}} = 243I^2 \)
一次銅損: \( P_{\mathrm{c1}} = 45I^2 \)
二次銅損: \( P_{\mathrm{c2}} = 27I^2 \)
これを使って、三相誘導電動機の効率 \( \eta \) [%] を求めていこか。効率の基本式は何やったっけ?
はい、先生!効率 \( \eta \) は「出力÷入力×100%」で表せます。電動機の場合、入力は出力と損失の合計ですので:
\[ \begin{aligned} \eta &= \frac{\text{出力}}{\text{入力}} \times 100[\%] \\ &= \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + P_{\mathrm{c1}} + P_{\mathrm{c2}}} \times 100[\%] \end{aligned} \]これに先ほど求めた値を代入すれば効率が求められます。
ほんまにええ感じやで!それじゃあ、求めた値を効率の式に代入してみ?
はい、先生!効率を計算します:
\[ \begin{aligned} \eta &= \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + P_{\mathrm{c1}} + P_{\mathrm{c2}}} \times 100[\%] \\ &= \frac{243I^2}{243I^2 + 45I^2 + 27I^2} \times 100[\%] \\ &= \frac{243I^2}{315I^2} \times 100[\%] \\ &= \frac{243}{315} \times 100[\%] \\ &\approx 77.14[\%] \\ &\approx 77[\%] \end{aligned} \]よって答えは選択肢の(2)となります。
素晴らしい!正解は77%、つまり選択肢の(2)やね!
この問題で大事なポイントをおさらいしておこか:
1. L形等価回路では励磁回路の電流を無視できる(\( I_0 = 0 \))
2. 出力パワーは \( P_{\mathrm{o}} = 3 \cdot \frac{1-s}{s} \cdot {r_2}' \cdot I^2 \) で求められる
3. 各銅損は抵抗×電流の二乗×相数(3)で計算できる
4. 効率は出力÷入力×100%で、入力は出力+全損失
こういう等価回路を使った計算は第三種電気主任技術者試験でよく出るから、しっかり理解しておいてな!
ありがとうございます、先生!三相誘導電動機のL形等価回路からの効率計算の流れがよく理解できました。特に滑り率を使った出力パワーの計算と、各損失の合計から効率を求める方法が重要なんですね。次回の学習でも活かしていきます!
解説まとめ
L 形等価回路において,励磁回路には電流が流れないので,\( I_{0} = 0 \),\( I_{1} = I_{2} = I \) とすると,出力 \( P_{\mathrm{o}} \),一次銅損 \( P_{\mathrm{c1}} \),二次銅損 \( P_{\mathrm{c2}} \) の大きさは,次のように求められる。
\[ \begin{aligned} P_{\mathrm{o}} &= 3 \frac{1 - s}{s} r_{2}' I^{2} \\[5pt] &= 3 \times \frac{1 - 0.1}{0.1} \times 9 I^{2} \\[5pt] &= 243 I^{2} \\[10pt] P_{\mathrm{c1}} &= 3 r_{1} I^{2} \\[5pt] &= 45 I^{2} \\[10pt] P_{\mathrm{c2}} &= 3 r_{2}' I^{2} \\[5pt] &= 27 I^{2} \end{aligned} \]
したがって,三相誘導電動機の効率 \( \eta \,[\%] \) は次のように求められる。
\[ \begin{aligned} \eta &= \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + P_{\mathrm{c1}} + P_{\mathrm{c2}}} \times 100 \\[5pt] &= \frac{243 I^{2}}{243 I^{2} + 45 I^{2} + 27 I^{2}} \times 100 \\[5pt] &= \frac{243}{243 + 45 + 27} \times 100 \\[5pt] &\approx 77\, [\%] \end{aligned} \]
よって答えは選択肢の(2)となる