【機械】平成23年 問4|三相誘導電動機の回転速度を制御するための抵抗値の計算問題
極数 \( 4 \) で \( 50 \) [Hz] 用の巻線形三相誘導電動機があり,全負荷時の滑りは \( 4 \) [%] である。
全負荷トルクのまま,この電動機の回転速度を \( 1\,200 \) [min\(^{-1}\)] にするために,二次回路に挿入する \( 1 \) 相当たりの抵抗 [\( \Omega \)] の値として,最も近いのは次のうちどれか。
ただし,巻線形三相誘導電動機の二次巻線は星形 \( \left( \mathrm{Y} \right) \) 結線であり,各相の抵抗値は \( 0.5 \) [\( \Omega \)] とする。
合格への方程式
L形等価回路の構造と意味
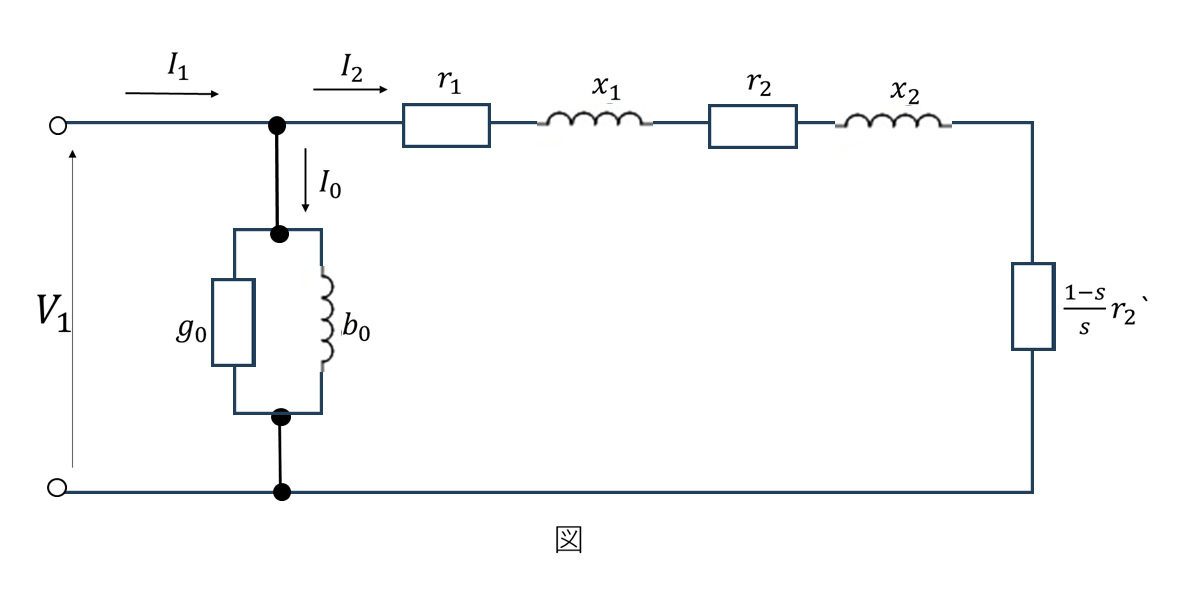
三相誘導電動機のL形等価回路は、電動機の電気的特性を解析するための基本モデルです。
回路各部の説明
L形等価回路の各部は以下の通りです:
- 電圧・電流
V̇1 [V]:一次側端子電圧(固定子に加わる電圧)
İ1 [A]:一次電流(固定子電流)
İ2' [A]:二次電流の一次換算値(回転子電流を固定子側に換算)
İ0 [A]:励磁電流(磁束を発生させるための電流)
- インピーダンス要素
r1 [Ω]:一次巻線抵抗(固定子巻線の抵抗)
r2' [Ω]:二次巻線抵抗の一次換算値(回転子巻線抵抗を固定子側に換算)
x1 [Ω]:一次漏れリアクタンス(固定子の漏れ磁束による)
x2' [Ω]:二次漏れリアクタンスの一次換算値(回転子の漏れ磁束による)
r2'/s [Ω]:滑りsで変化する等価抵抗(機械的出力を表現)
L形等価回路の特徴
・励磁回路(İ0)を一次側に配置し、回路形状がL字型になっている
・二次側回路に滑りsによって変化する抵抗r2'/sを導入
・この抵抗r2'/sが、電気エネルギーから機械エネルギーへの変換を表現
・一次換算により、変圧器のように一次側から二次側の特性を統一的に扱える
注意点
・この等価回路は定常状態の解析に有効であり、過渡状態の解析には適さない
・実際の機器では鉄損などの要素も考慮する必要がある
・周波数が変化する場合、リアクタンス値も変化することに注意
同期速度と滑り
誘導電動機の動作原理を理解するうえで重要な同期速度と滑りについて解説します。
同期速度の計算
三相誘導電動機の同期速度Ns [min-1]は、極数pと電源周波数f [Hz]から次式で求められます:
\[ \begin{aligned} N_{\mathrm{s}} &= \frac{120f}{p} \\[10pt] \end{aligned} \]
この式の「120」は、60(秒/分の換算)× 2(極対数から極数への換算)から来ています。
| 極数 p | 50Hz系統の同期速度 [min-1] | 60Hz系統の同期速度 [min-1] |
|---|---|---|
| 2 | 3000 | 3600 |
| 4 | 1500 | 1800 |
| 6 | 1000 | 1200 |
| 8 | 750 | 900 |
滑りの定義と計算
滑りsは、同期速度Nsと実際の回転速度N [min-1]の差を同期速度で割った値です:
\[ \begin{aligned} s &= \frac{N_{\mathrm{s}}-N}{N_{\mathrm{s}}} \\[10pt] \end{aligned} \]
実際の回転速度Nは滑りを使って次のように表されます:
\[ \begin{aligned} N &= N_{\mathrm{s}}-sN_{\mathrm{s}} \\[10pt] &= (1-s)N_{\mathrm{s}} \\[10pt] \end{aligned} \]
滑りの意味と範囲
・s = 0:同期速度で回転(実際の誘導機では実現しない理論値)
・0 < s < 1:電動機運転領域(通常は全負荷時で s = 0.02~0.05程度)
・s = 1:回転子が静止している状態(始動時)
・s > 1:逆転制動領域(電源の相順と逆方向に回転)
・s < 0:発電機運転領域(同期速度以上で回転)
応用例
例えば、4極の誘導電動機が60Hz電源で運転され、回転速度が1746rpm測定された場合の滑りは:
Ns = 120 × 60 / 4 = 1800 rpm
s = (1800 - 1746) / 1800 = 0.03 = 3%
このように、滑りは電動機の負荷状態を示す重要な指標となります。
出力と損失の関係
L形等価回路を用いた三相誘導電動機の出力、損失、効率の解析について説明します。
出力と損失の計算式
図のL形等価回路から、以下の重要な関係式が導かれます:
\[ \begin{aligned} P_{\mathrm{o}} &= 3\frac{1-s}{s}r_{2}^{\prime}{I_{2}^{\prime}}^{2} \\[10pt] P_{\mathrm{c2}} &= 3r_{2}^{\prime}{I_{2}^{\prime}}^{2} \\[10pt] P_{2} &= P_{\mathrm{o}}+P_{\mathrm{c2}} = 3\frac{r_{2}^{\prime}}{s}{I_{2}^{\prime}}^{2} \\[10pt] \end{aligned} \]
ここで、
Po [W]:機械的出力
Pc2 [W]:二次銅損(回転子での熱損失)
P2 [W]:二次入力(回転子に入る電力)
出力・損失の比例関係
これらの式から、次の重要な比例関係が導かれます:
\[ \begin{aligned} P_{2}:P_{\mathrm{o}}:P_{\mathrm{c2}} &= 1:(1-s):s \\[10pt] \end{aligned} \]
この関係は、電動機の滑りsが小さいほど、二次入力のうち機械的出力に変換される割合が高くなることを示しています。
計算例
例えば、滑り s = 0.04(4%)の場合:
P2 : Po : Pc2 = 1 : 0.96 : 0.04
つまり、回転子に入力される電力の96%が機械的出力に変換され、4%が回転子での熱損失になります。
損失の全体像
誘導電動機の損失は以下のように分類されます:
1. 一次銅損:Pc1 = 3r1I12
2. 二次銅損:Pc2 = 3r2'I2'2 = sP2
3. 鉄損:Pi(ヒステリシス損と渦電流損)
4. 機械損:Pm(摩擦損と風損)
5. 漂遊負荷損:Ps(その他の負荷に依存する損失)
効率の計算
三相誘導電動機の効率η [%]は次式で計算されます:
\[ \begin{aligned} \eta &= \frac{P_{\mathrm{o}}}{P_{\mathrm{in}}} \times 100\% \\[10pt] &= \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + \text{全損失}} \times 100\% \\[10pt] \end{aligned} \]
一般的な三相誘導電動機の効率は、サイズや設計によりますが、75%~95%程度です。
トルク特性
三相誘導電動機のトルク特性と、それを支配する要因について解説します。
トルクの基本式
L形等価回路から導かれる三相誘導電動機のトルクT [N·m]は次式で表されます:
\[ \begin{aligned} T &= \frac{1}{\omega_{\mathrm{s}}}\frac{3V_{1}^{2}\frac{r_{2}^{\prime}}{s}}{\left(r_{1}+\frac{r_{2}^{\prime}}{s}\right)^{2}+\left(x_{1}+x_{2}^{\prime}\right)^{2}} \\[10pt] \end{aligned} \]
ここで、ωs [rad/s]は同期角速度です。
低滑り時の近似式
滑りが小さい運転領域(s ≪ 1)では、トルク式は次のように近似できます:
\[ \begin{aligned} T &\simeq \frac{3V_{1}^{2}s}{\omega_{\mathrm{s}}r_{2}^{\prime}} \\[10pt] \end{aligned} \]
この近似式から、低滑り領域ではトルクは滑りsに比例することがわかります。
巻線形誘導電動機の特性
巻線形誘導電動機では、二次抵抗r2'を外部から調整できます。一定トルクの場合、次の関係が成り立ちます:
\[ \begin{aligned} \frac{r_{2}^{\prime}}{s} &= \text{一定} \\[10pt] \end{aligned} \]
これは、二次抵抗r2'を増加させると、同じトルクを発生するために必要な滑りsも比例して増加することを意味します。
トルク-速度特性曲線
誘導電動機のトルク-速度特性は以下の特徴を持ちます:
・始動トルク(s = 1):始動時に発生するトルク
・最大トルク(s = sm):運転中に発生可能な最大トルク
・定格トルク:定格出力時のトルク
・低滑り領域(s ≪ 1):トルクはほぼ滑りに比例
二次抵抗変化の影響
巻線形誘導電動機で二次抵抗を増加させると:
・始動トルクが増加
・最大トルクは変化しないが、最大トルク発生時の滑りが増加
・速度変動が大きくなる(速度制御に利用可能)
・二次銅損が増加するため効率は低下
速度制御方法
三相誘導電動機の主な速度制御方法について解説します。
基本的な速度制御法
誘導電動機の速度N [min-1]は、次式で表されます:
\[ \begin{aligned} N &= (1-s)N_{\mathrm{s}} \\[10pt] &= (1-s)\frac{120f}{p} \\[10pt] \end{aligned} \]
この式から、速度制御には以下の3つの方法があることがわかります:
1. 極数pの変更:極数切替による段階的な速度制御
2. 周波数fの変更:インバータなどによる連続的な速度制御
3. 滑りsの調整:二次抵抗の変更などによる速度制御
1. 極数変更による速度制御
・方法:特殊な固定子巻線を用いて極数を切り替え
・特徴:2段~4段程度の段階的な速度制御が可能
・利点:効率低下が少ない、構造が比較的簡単
・欠点:連続的な速度制御ができない、速度比は限定される
・応用例:エレベータ、旧式のポンプ・送風機など
2. 周波数制御(可変周波数制御)
・方法:インバータを用いて電源周波数を変更
・特徴:広範囲かつ連続的な速度制御が可能
・V/f制御:周波数fと電圧Vの比を一定に保ち磁束を一定に維持
\[ \begin{aligned} \frac{V}{f} &= \text{一定} \\[10pt] \end{aligned} \]
・利点:効率良く広範囲の速度制御が可能、始動電流が小さい
・欠点:インバータが必要で装置が高価になる
・応用例:工作機械、エレベータ、ポンプ、送風機など
3. 滑り制御
・巻線形誘導電動機の二次抵抗制御
- 方法:二次巻線に接続された可変抵抗を調整
- 特徴:始動トルクが大きく、速度制御範囲は限定的
- 欠点:二次抵抗で消費されるエネルギーにより効率が低下
・二次側インバータ制御(回生制御)
- 方法:二次側にインバータを接続して滑りパワーを回生
- 特徴:高効率で連続的な速度制御が可能
- 応用例:大型ポンプ、圧延機、巻上機など
速度制御範囲の比較
| 速度制御方法 | 制御範囲 | 効率 | コスト |
|---|---|---|---|
| 極数切替 | 段階的(2~4段階) | 高 | 中 |
| 周波数制御 | 連続的(広範囲) | 高 | 高 |
| 二次抵抗制御 | 連続的(狭範囲) | 低 | 中 |
| 二次側インバータ | 連続的(中範囲) | 高 | 高 |
応用と実例
三相誘導電動機の産業応用と特性の活用について解説します。
産業用途別の特性活用
1. 定速運転用途
・特性:低滑り、高効率
・応用例:ポンプ、コンプレッサ、送風機、工作機械
・使用技術:かご形誘導電動機、直入れ始動
2. 可変速運転用途
・特性:速度制御性、トルク特性
・応用例:クレーン、エレベータ、巻上機、製紙機械
・使用技術:インバータ制御、巻線形誘導電動機
3. 高始動トルク用途
・特性:高始動トルク、頻繁な始動停止
・応用例:圧延機、破砕機、大型コンベア
・使用技術:特殊かご形、巻線形誘導電動機
電力コスト削減事例
・ポンプ・送風機のインバータ制御
- 流量制御にインバータによる速度制御を採用
- バルブやダンパーによる絞り調整と比べて大幅な省エネが可能
- 流量が半分の場合、消費電力は約1/8に低減
・エレベータの回生ブレーキ制御
- 下降時のエネルギーを電力系統に回生
- 約20~30%の省エネ効果
負荷特性に合わせた電動機選定
1. 定トルク負荷:コンベア、圧延機など
- 負荷トルクが速度に関わらずほぼ一定
- 広範囲の速度制御にはインバータのベクトル制御が有効
2. 二乗トルク負荷:ポンプ、送風機など
- 負荷トルクが速度の二乗に比例
- インバータのV/f制御で効率的な速度制御が可能
3. 定出力負荷:巻取機、放出機など
- 低速では高トルク、高速では低トルクが必要
- 弱め界磁制御が有効
誘導電動機選定のポイント
・容量:最大負荷の1.1~1.2倍程度の余裕
・始動特性:負荷の始動トルク要求を満たすか
・速度変動:負荷変動に対する速度変動の許容範囲
・環境条件:防水、防塵、防爆などの特殊要件
・効率クラス:IE3(プレミアム効率)以上の高効率モータの採用
🔍 ワンポイントアドバイス: 三相誘導電動機のL形等価回路は、見かけ上複雑ですが、各要素が持つ物理的な意味を理解すれば解析しやすくなります。特に「r2'/s」という滑りに依存する抵抗が、電気エネルギーから機械エネルギーへの変換を表現していることがポイントです。また、「二次入力:出力:二次銅損 = 1:(1-s):s」という比例関係は、滑りsが小さいほど効率が良いことを簡潔に表現しています。巻線形誘導電動機では「r2'/s = 一定」の関係を用いた速度制御が可能であり、これは産業用途では非常に重要な特性です。
今日は三相誘導電動機の問題やで!極数 \( p=4 \)、周波数 \( f=50 \ \mathrm{[Hz]} \) の三相誘導電動機について考えるで。まずは同期速度 \( N_{\mathrm{s}} \ \mathrm{[{min}^{-1}]} \) を求めてみよか?
はい、先生!同期速度 \( N_{\mathrm{s}} \) は極数 \( p \) と周波数 \( f \) から求められます。公式は次のようになります:
\[ \begin{eqnarray} N_{\mathrm{s}} &=& \frac{120f}{p} \\[20pt] &=& \frac{120 \times 50}{4} \\[20pt] &=& 1 \ 500 \ \mathrm{[{min}^{-1}]} \end{eqnarray} \]この公式の「120」は、60秒/分 × 2(1周期で北極と南極の2回転分)という意味があります。
ええやん!同期速度 \( N_{\mathrm{s}} = 1 \ 500 \ \mathrm{[{min}^{-1}]} \) が計算できたな!さて、この三相誘導電動機の全負荷時の滑り \( s=0.04 \) やけど、回転速度 \( N=1 \ 200 \ \mathrm{[{min}^{-1}]} \) のときの滑り \( s' \) はどうなるやろ?滑りの定義から考えてみい!
はい!滑り \( s \) は同期速度 \( N_{\mathrm{s}} \) と実際の回転速度 \( N \) の差を同期速度で割ったものですね。数式で表すと:
\[ \begin{eqnarray} s' &=& \frac{N_{\mathrm{s}} - N}{N_{\mathrm{s}}} \\[20pt] &=& \frac{1 \ 500 - 1 \ 200}{1 \ 500} \\[20pt] &=& \frac{300}{1 \ 500} \\[20pt] &=& 0.2 \end{eqnarray} \]つまり、回転速度が \( N=1 \ 200 \ \mathrm{[{min}^{-1}]} \) のときの滑りは \( s'=0.2 \) となります。これは全負荷時の滑り \( s=0.04 \) よりも大きいので、速度が大きく低下していることがわかります。
よっしゃ!滑りの計算もバッチリやな。さて、問題の最後のパートやけど、二次回路に挿入する \( 1 \) 相当たりの抵抗 \( R \ \mathrm{[\Omega]} \) を求めるんや。各相の抵抗値 \( r_2=0.5 \ \mathrm{[\Omega]} \) が与えられてるで。この問題は巻線形誘導電動機のトルクの比例推移を使うんやけど、どないして求めるか考えてみい?
はい、先生!巻線形誘導電動機では、二次側に抵抗を挿入することでトルク特性を変えることができますね。
トルクを一定に保つための条件は、\( \frac{r_2}{s} = \frac{r_2 + R}{s'} \) です。この式を使って未知の抵抗 \( R \) を求めてみます:
\[ \begin{eqnarray} \frac{r_2}{s} &=& \frac{r_2 + R}{s'} \\[20pt] \frac{0.5}{0.04} &=& \frac{0.5 + R}{0.2} \\[20pt] \end{eqnarray} \]左辺を計算すると:
\[ \begin{eqnarray} \frac{0.5}{0.04} &=& 12.5 \end{eqnarray} \]この式を \( R \) について解きます:
\[ \begin{eqnarray} 12.5 &=& \frac{0.5 + R}{0.2} \\[20pt] 12.5 \times 0.2 &=& 0.5 + R \\[20pt] 2.5 &=& 0.5 + R \\[20pt] R &=& 2.5 - 0.5 \\[20pt] R &=& 2.0 \ \mathrm{[\Omega]} \end{eqnarray} \]したがって、二次回路に挿入する \( 1 \) 相当たりの抵抗は \( R = 2.0 \ \mathrm{[\Omega]} \) となります。
よって、答えは選択肢の(1)です!
完璧や!抵抗値 \( R = 2.0 \ \mathrm{[\Omega]} \) が正しく求められたな。今回の問題で学んだことをまとめてみよか?
はい、先生!今回の問題から学んだポイントは:
1. 三相誘導電動機の同期速度は \( N_{\mathrm{s}} = \frac{120f}{p} \) で求められます。
2. 滑り \( s \) は同期速度と実際の回転速度の差の割合で、\( s = \frac{N_{\mathrm{s}} - N}{N_{\mathrm{s}}} \) で表されます。
3. 巻線形誘導電動機では、二次側に抵抗を挿入することで、速度を調整できます。
4. トルクを一定に保つための条件は \( \frac{r_2}{s} = \frac{r_2 + R}{s'} \) です。この式から必要な二次抵抗を計算できます。
5. 滑りが大きいほど、回転速度は同期速度から離れて小さくなります(\( s=0.2 \) は \( s=0.04 \) より速度が遅い状態)。
解説まとめ
題意より、極数 \( p = 4 \)、周波数 \( f = 50 \mathrm{Hz} \) であるから、同期速度 \( N_{\mathrm{s}} \) は、以下のように求められる。
$$ \begin{aligned} N_{\mathrm{s}} &= \frac{120f}{p} \\[5pt] &= \frac{120 \times 50}{4} \\[5pt] &= 1500 \, \mathrm{min}^{-1} \end{aligned} $$
全負荷時の滑り \( s = 0.04 \) であり、回転速度 \( N = 1200 \, \mathrm{min}^{-1} \) のときの滑り \( s' \) は、次のように求められる。
$$ \begin{aligned} s' &= \frac{N_{\mathrm{s}} - N}{N_{\mathrm{s}}} \\[5pt] &= \frac{1500 - 1200}{1500} \\[5pt] &= 0.2 \end{aligned} $$
また、各相の抵抗値 \( r_{2} = 0.5\, \Omega \) であることから、二次回路に挿入する1相当たりの抵抗 \( R \) は、次のように求められる。
$$ \begin{aligned} \frac{r_{2}}{s} &= \frac{r_{2} + R}{s'} \\[5pt] \frac{0.5}{0.04} &= \frac{0.5 + R}{0.2} \\[5pt] \frac{0.5}{0.04} \times 0.2 &= 0.5 + R \\[5pt] 2.5 &= 0.5 + R \\[5pt] R &= 2.0\, \Omega \end{aligned} $$